昨日の記事に引き続きPCAを使っていきたいと思います。LDAの説明をする予定だったのですが、ちょっと予定を変えて今日もPCAのみです。
カオスの中に...##
43000個の手書き数字データをPCAで2次元に落としてグラフにしたのが下記です。
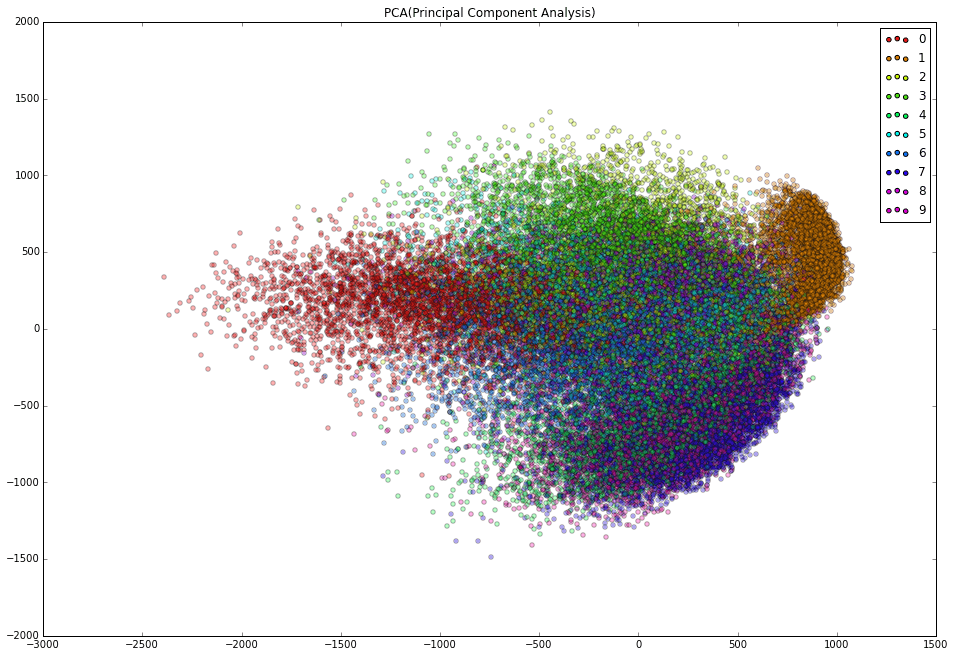
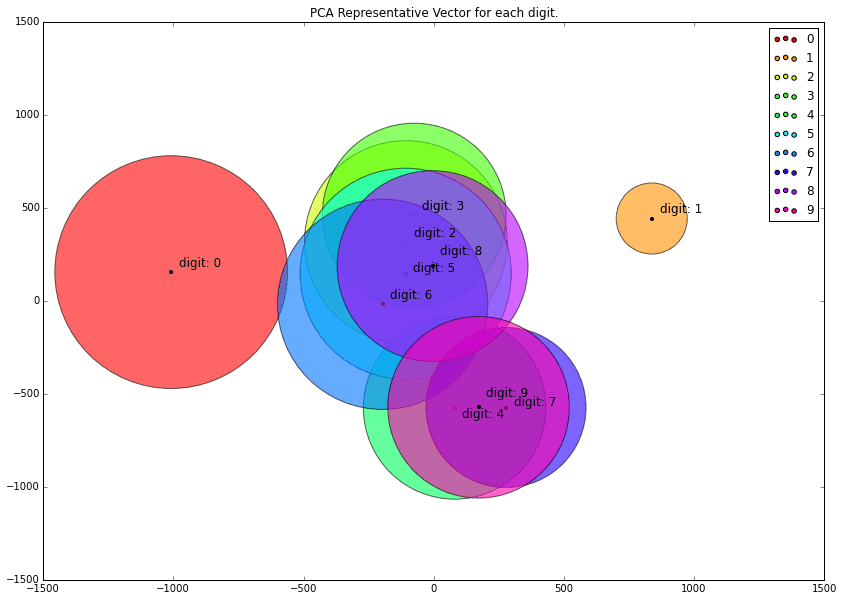
手書き文字784次元を2次元に落とすという無茶な分析をした結果のグラフがこれですね。"1"とか"0"とかはわりと分離できているのですが、"2","3","5","6","8"で1つグループ、"4","7","9"でもう1つのグループとして重なっちゃっていますね。。。特に上のグラフはカオスです。。。
でも、2次元から30次元ぐらいまで主成分を増やすと積寄与率が0.731と7割を超えるので、意外と良い結果にるんじゃないかなという予感がします。
寄与率を出すpythonコードはこちら。ライブラリを使うと簡単ですね^^
n_comp = 30
pca = decomp.PCA(n_components = n_comp)
pca.fit(dataset.getData()) # 43000個全ての手書き数字に主成分分析をかける
E = pca.explained_variance_ratio_
print "explained", E # 各主成分の寄与率
print "cumsum E", np.cumsum(E) # 累積寄与率
主成分の視覚化###
では、この主成分と、次元削減後のデータでどこまで表現できるかを試してみたいと思います。
今回の例では784次元から30次元にデータを圧縮しています。よって主成分が30個あるので
{\bf a_1} = \{ a_{1,1},a_{1,2},a_{1,3},...,a_{1,784} \} \\
... \\
{\bf a_{30}} = \{ a_{30,1},a_{30,2},a_{30,3},...,a_{30,784} \}
と表すことができ、これと数字のデータ"0"は
{\bf x_0} = \{ x_{0,1},x_{0,2},x_{0,3},....x_{0,30} \}
という成分が30個のベクトルで表すことができます。今まで784個の成分の大きなベクトルを使わないと表現できなかったことが30個の成分で表すことができるところに主成分分析の意味がありますね。
そこで、これを画像データに戻すために、
ImageData_0 = x_{0,1}{\bf a_1} + x_{0,2}{\bf a_2} + ... + x_{0,30}{\bf a_30}
という計算をします。
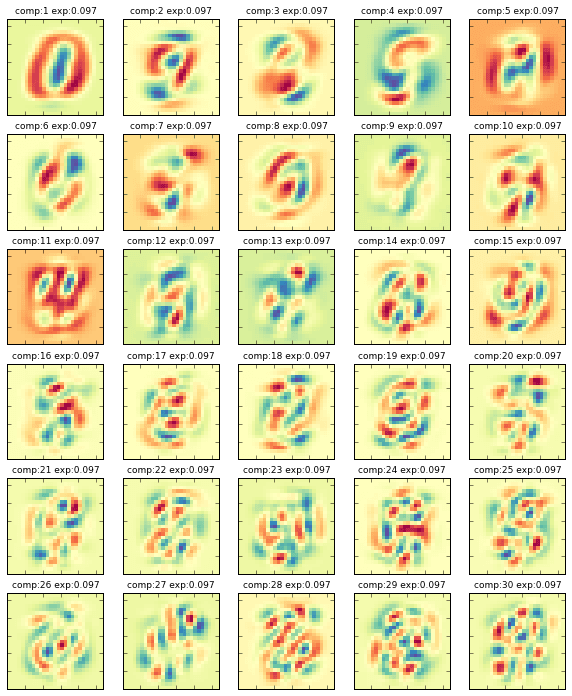
まず、各主成分${\bf a_i}$を画像で表すとどのようになるかをグラフィカルに確認したいと思います。左上から順に${\bf a_1},{\bf a_2} , ...$です。
うわっ、なんだかカオスというより気持ち悪いグラフになりましたね。。。
本当に大丈夫だろうか。。。心配。。。
この主成分をグラフにするpythonコードはこちら。
n_comp = 30
fig = plt.figure(figsize=(10, 12))
for i in range(n_comp):
plot_digits(pca.components_[i], size, 6, 5, i+1, "comp:%d exp:%.3f" % (i+1, E[0]), fontsize=9)
plt.savefig("PCA components.png")
plt.show()
### 30次元に落とした数字データを画像表示する###
ちなみに各数字のデータは下記のような30次元ベクトルです。
0 [-1701.4516848 360.5515562 501.80559391 335.42365557 -442.37893255
738.40404869 653.87543763 -176.60067741 7.52017489 67.8462729
-34.2218036 -46.55184177 -70.43577469 -342.69209695 377.83995173
-5.66582709 317.76574823 -87.61261823 -94.53116795 175.02827
-213.08659782 272.41196629 7.16761158 -22.635149 -34.60858894
-264.48697639 -76.62192789 14.02612973 -80.42733958 87.6849867 ]
1 [ 661.59577975 699.31132821 -183.28203965 120.61139445 -81.08181052
489.46188551 -683.47083797 85.55938661 -348.5480522 202.97854522
364.55994931 -21.26575592 404.44144851 -97.05254548 61.83993555
-86.78002717 17.65814358 -285.48469649 18.82730277 -207.64273128
44.24360034 -221.89436971 57.22745918 -148.67496175 14.34358893
41.55603106 -333.7236588 208.97888078 59.81363057 -84.55446472]
2 [ 2.61889858 667.83425383 623.25708606 -240.73842216 807.87987427
448.08932462 809.91470435 -532.39654183 -541.55909038 172.17476512
-9.56195501 282.15421246 219.11044719 -220.93747327 43.0973319
146.33386437 181.93836014 116.40958486 13.92428748 -105.6101748
185.89765605 -291.55100581 87.49435262 84.58855469 145.02361174
51.72930638 47.85132163 261.13345514 -24.44843863 50.79510831]
3 [ 114.38181469 20.72714258 504.58355599 -89.64933421 -253.97294532
325.980776 -360.69326214 66.35769716 -14.68477165 -130.43479691
-447.40395968 111.99175081 -31.50682548 183.41780399 -519.83792854
-256.85478577 -113.73387925 -342.03579127 -252.46793099 42.67143142
-127.42356394 186.64626798 181.90229759 219.77068914 -163.18068948
135.98266763 131.31762106 264.38488399 133.3078287 7.35507795]
4 [ 165.75560243 -300.18276053 64.14548517 759.70626076 -425.8443787
157.39033697 -304.0991401 276.40898204 45.86721541 -295.47758088
2.74648031 256.88429711 -87.73418977 -175.36126677 40.05170784
-87.53632407 54.27888133 -199.84899771 -11.82620089 -298.09170974
-232.16000555 89.85484106 292.73288896 125.82278044 -68.7010304
193.42367936 -184.23850425 82.89710955 214.44949617 -191.17837477]
5 [-350.22936554 -141.01297399 389.03065738 -619.26138386 288.79058105
-500.15719527 -538.72021671 -205.96174636 365.50575542 -60.49472136
44.4873806 -135.66792908 -112.30051758 592.00954779 211.90849699
-222.04781047 76.68101573 -173.22893185 -74.82330789 -328.13687912
54.20947384 29.24886881 -54.30828897 109.31639119 -148.5643377
231.27705194 -56.10174144 104.02362596 -5.79036367 127.80551682]
6 [-187.86580218 90.04418067 -744.54442254 350.31041481 -332.06715871
-180.95934671 -162.1086696 16.39830485 -374.48172442 83.73143967
130.89870535 80.7921533 -8.58842498 84.6122807 -146.77018343
-138.92568721 158.65298533 103.19544849 -212.53071491 -278.06266361
176.32032658 318.61200636 -25.04615495 -331.00041428 -68.16511766
-8.6657172 131.68031183 163.86737242 80.71525 17.82871763]
7 [ 672.32316444 -464.80397448 313.66005881 -136.13073047 -325.54440893
352.67672269 333.35838571 149.05717471 110.00701405 233.97083611
202.69128282 -211.99648309 -121.59390141 -235.10689307 -183.46670371
-262.11364747 164.16735123 -102.47910648 257.00098676 -242.83922531
-205.03185461 85.07389889 159.82922651 -153.57362576 15.46211732
-282.58840157 38.47973654 40.80311292 -28.29748845 -68.67282582]
8 [ -2.63682307e+02 -3.92782426e+02 -4.82817090e+02 -1.08732309e+03
3.16636550e+02 9.40608014e+01 9.62990473e+00 -3.44484518e+02
-3.42655267e+02 2.44390233e+02 -3.28347935e+02 1.00384644e+00
4.64562686e+02 -3.92400283e+02 -1.99550884e+01 2.25400966e+02
-3.93818241e+02 -1.72862773e+02 6.53585372e+01 -2.10524955e+02
3.71808324e+02 7.97760442e+01 1.02030888e+02 -2.09960791e+02
-1.65077930e+02 3.51481675e+02 1.99475148e+02 -3.71063678e+02
6.48734732e+01 -1.68703356e+02]
9 [ 306.52927212 -351.81955452 -469.10137206 -647.33110927 112.86683552
215.02556985 -54.15071035 -363.34083069 -211.26631969 -706.20430501
8.02149574 249.34094422 -166.86167523 211.93010084 -226.5338007
85.19449155 185.16142027 148.70012599 -141.61039606 200.31039523
116.4385829 282.81894609 40.49368393 49.44160736 -236.56002282
42.07184296 -210.24357152 -226.30974581 166.15458766 175.76515424]
で、このベクトルの成分一つ一つに主成分のベクトルをかけてデータを復元します。大丈夫かな、さっきの主成分で・・・
計算を実行したpythonコードはこちら。
# 各数字から1つずつ次元削減後のデータを取ってくる
transformed = [pca.transform(dataset.getByLabel(i, num=1)) for i in range(10)]
label_data_10dim = []
for l in range(10):
vec = []
for i, t in zip(range(len(transformed[l][0])), transformed[l][0]):
vec.append(t * np.array(pca.components_[i])) # データの要素と主成分のベクトルを掛け合わせる。
S = np.sum(vec,axis=0) # 各要素ごとに足し合わせる。
label_data_10dim.append(S)
# 画像表示
fig = plt.figure(figsize=(10, 5))
for i in range(10):
plot_digits(label_data_10dim[i], size, 2, 5, i+1, "label:%d"%i, fontsize=9)
plt.show()
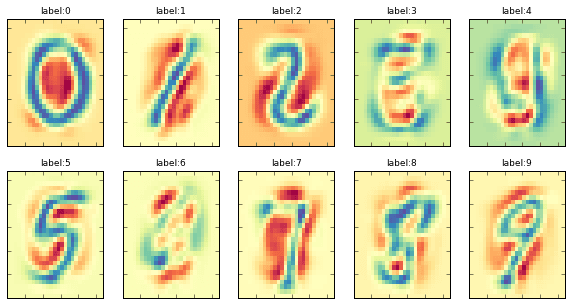
で、表示させたのがこちらです。
想像以上に表現できている! "0","1","2","5","7","8","9"は問題なく読めますね。
"3"は薄目で見てみてください。よーくみると3がちゃんと現れています!"4"と"6"はちょっと厳しい結果ですね。でも、先ほどの謎の主成分から結構数字画像が復元できていると思います。