手書き数字データをイメージ表示する##
まず、手書き数字データを準備します。今回はKaggleのDigital Recognizerという課題からtrainという名の教師データをダウンロードして使いたいと思います。
このデータ全部を使うと73MBとかなりのデータ量のため、分かりやすさを優先して0〜9の各数字から20個ずつ、計200個をピックアップして使います。ピックアップしたデータはここからダウンロードしてください。
この手書き数字データはCSVファイルとなっていて
```のように、1桁目はどの数字が書かれたかを表すラベル、それ以降の桁は28x28=784ピクセル分の数字データが続きます。
まずは必要なライブラリをインポートします。
```py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
そしてデータを読み込んで配列に格納、ラベル順でソートします。
size = 28
raw_data= np.loadtxt('train_small.csv',delimiter=',',skiprows=1)
digit_data = []
for i in range(len(raw_data)):
digit_data.append((raw_data[i,0],raw_data[i,1:785]))
digit_data.sort(key=lambda x: x[0]) # sort array by label
まずは読み込んだデータがどんな画像なのか、イメージで表示して(matplotlibのpcolorグラフで)みてみます。
# draw digit images
plt.figure(figsize=(15, 15))
for i in range(len(digit_data)):
X, Y = np.meshgrid(range(size),range(size))
Z = digit_data[i][1].reshape(size,size) # convert from vector to 28x28 matrix
Z = Z[::-1,:] # flip vertical
plt.subplot(10, 20, i+1) # layout 200 cells
plt.xlim(0,27)
plt.ylim(0,27)
plt.pcolor(X, Y, Z)
plt.flag()
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
plt.show()
"2"の8番目のデータがすごいですね、"2"の面影がありません(笑) "2"だと言われなければ人間でも判別できないのではないでしょうか・・・
これが今回使用するデータセットです。
各データ間の相関を取ってみる##
相関行列をプロットする###
この28x28=784ピクセルの画像データを、784次元ベクトルで各要素をグレースケールの濃さとして相関行列を作ってみます。単純に相関をとることがどの程度意味を持つかは課題ですが、簡易な方法で画像同士の近さが多少は表せる気がします。
200x200の行列なので数字にしても全く理解できないのでイメージをつかむためグラフで表します。
なかなか壮観なグラフですね(笑)
完全な対角成分は、同じデータなので相関が1です。薄目で見てみると対角ブロック(同じ数字同士の相関係数)がちょっと濃いような気がします。"1"は確実に相関が高いです。
pythonでの計算は下記のように行っています。
data_mat = []
# convert list to ndarray
for i in range(len(digit_data)):
label = digit_data[i][0]
data_mat.append(digit_data[i][1])
A = np.array(data_mat)
Z = np.corrcoef(A) # generate correlation matrix
area_size = len(digit_data)
X, Y = np.meshgrid(range(area_size),range(area_size))
閾値を設けて見やすくする###
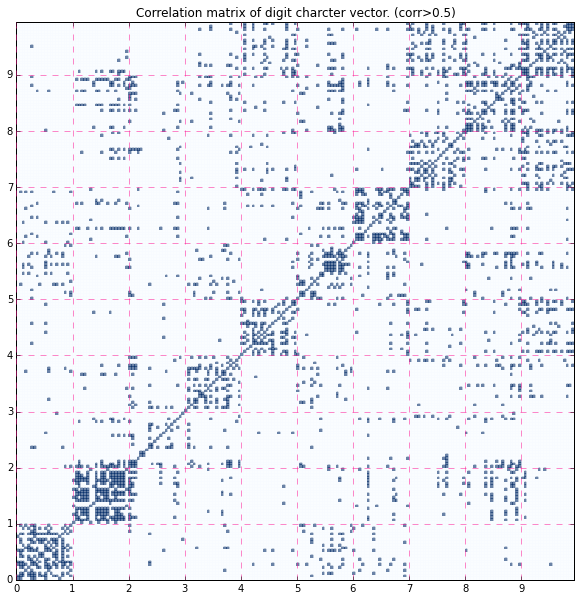
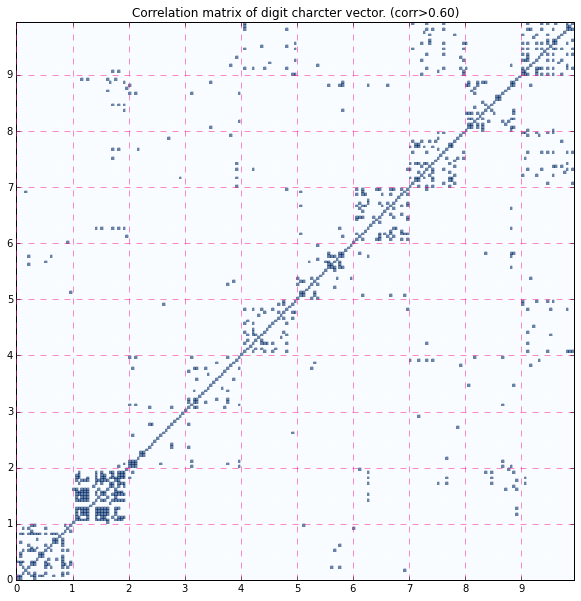
もうちょっと見やすくするために、閾値を設けを、相関係数がそれ超えているものを1, 未満のものを0と2値化してプロットしてみます。閾値として0.5, 0.6を選んでいますが恣意的なもので、いくつか試して対角成分が浮き上がり始めたものをピックアップしています。0.6のものを見るとだいぶ対角ブロックと、それ以外で差があるように見えてきました。"9"と"7"が似ている、ということも表されているようです。"2"は特に"2"同士の相関が低いことがわかります。
plt.clf()
plt.figure(figsize=(10, 10))
plt.xlim(0,area_size-1)
plt.ylim(0,area_size-1)
plt.title("Correlation matrix of digit charcter vector. (corr>0.5)")
thresh = .5
Z1 = Z.copy()
Z1[Z1 > thresh] = 1
Z1[Z1 <= thresh] = 0
plt.pcolor(X, Y, Z1, cmap=cm.get_cmap('Blues'),alpha=0.6)
plt.xticks([(i * 20) for i in range(10)],range(10))
plt.yticks([(i * 20) for i in range(10)],range(10))
plt.grid(color='deeppink',linestyle='--')
plt.show()
ブロックごとの平均値###
最後に、ブロックごとの平均値を10x10のグラフで表してみます。
summary_Z = np.zeros(100).reshape(10,10)
for i in range(10):
for j in range(10):
i1 = i * 20
j1 = j * 20
#print "[%d:%d,%d:%d]" % (i1,i1+20,j1,j1+20)
if i==j:
# 対角成分は1に決まっているので、値が上ぶれするのを避けるため除いて平均をとる
summary_Z[i,j] = (np.sum(Z[i1:i1+20,j1:j1+20])-20)/380
else:
summary_Z[i,j] = np.sum(Z[i1:i1+20,j1:j1+20])/400
# average of each digit's grid
plt.clf()
plt.figure(figsize=(10, 10))
plt.xlim(0,10)
plt.ylim(0,10)
sX, sY = np.meshgrid(range(11),range(11))
plt.title("Correlation matrix of summuation of each digit's cell")
plt.xticks(range(10),range(10))
plt.yticks(range(10),range(10))
plt.pcolor(sX, sY, summary_Z, cmap=cm.get_cmap('Blues'),alpha=0.6)
plt.show()
次のステップに向けて###
今回は、画像データを784次元ベクトルとみなして、そのベクトル間のそのまま相関をとるという、ある意味乱暴な分析をしてみましたが、本来画像データは2次元なので、上下左右等近隣ピクセルの値も考慮した近さを検討した方がよりもっともらしい画像同士の近さが表現できると思います。まだ、この段階だと機械学習以前ですね。でも、以外と対角成分がきちんとでていました。もう少し本格的なことは次のステップとして次回の記事で書いていこうと思います。