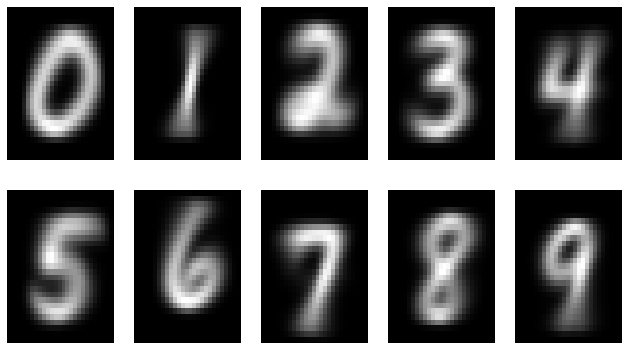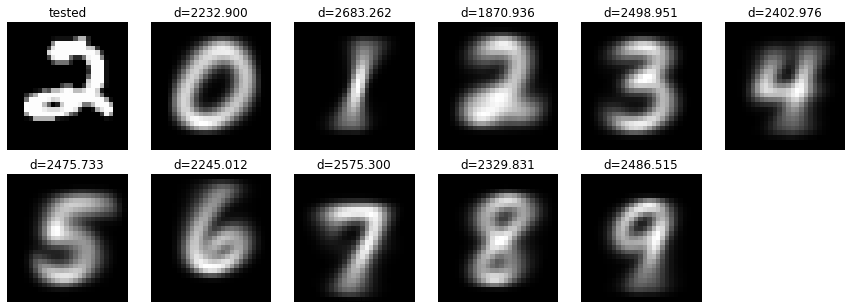手書き数字をpythonでもてあそぶ その２（識別する）

##手書き数字データを識別する##
前回の記事で手書き数字データの読み込みと画像化、あとは相関を見るということをやりましたが、今回はその数字が何の数字なのかの識別をやっていきたいと思います。

手書き数字の識別なので、与えられたデータが0〜9の10個のクラスのうちどれに該当するかを識別することを行います。なのでまず、

C = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}

の10個のクラスを定義します。

機械学習の方式の１つに「教師あり学習」と言うものがありますが、このパターンを使います。教師あり、とは事前に正解のデータを一定数蓄積し分析をしておくことで、識別するために必要な識別機を作成し、実際に識別したいデータをこの識別器にインプットして識別するやり方です。この事前に準備しておくデータを教師データと呼びます。

####テンプレートマッチング###
今回はテンプレートマッチング法を使って、数字を認識することをやってみたいと思います。
各ラベル（ここでは数字0～9）の代表値を定義し、識別器を作っていきます。今回は教師データの平均値を代表値とします。この代表値と渡された識別対象データの距離を計算し一番距離が短い代表値のクラスに属すると言うことにします。

前回"train_small.csv"の手書き数字データを扱っていましたが、今回はそのフルデータ版"train.csv"(42,000個のデータ)を教師データとして利用し、学習します。数字データは28x28の画像データを使っていますので784次元ベクトルで表現でき、教師データのそれぞれは

y_i= (y_1, y_2,...,y_{784}) 　　　　　 (i=0,1,...,9)

と表現します。$i$は各数字のクラスです。

ここでは代表値を $\hat{y}_i$と記します。

たとえば数字8のクラスの代表値は $\hat{y}_8$ です。平均で代表値は下記になります。

$n_i$ は各数字毎の教師データの数です。

\hat{y}_i = \frac{1}{n_i}\sum_{j=1}^{n_i} y_j

さて、識別対象のターゲットデータを$x_j$と表すと

x_j= (x_1, x_2,...,x_{784})

と、やはり784次元ベクトルで表されますので、識別機としては

{\rm argmin}_i{({\rm distance}_i)} = {\rm argmin}_i{(\|\hat{y}_i - x_j\|)}

を使います。

###代表値の導出と表示###
実際に計算していきます。最初に必要なライブラリをインポート。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict

ユーティリティーとしての関数を定義します。1桁目がラベル、以降がデータなのでそれを分割してクラスごとに分類する関数add_image()、ラベルごとの数をカウントする関数count_label()、グラフ描画のplot_digits()です。

image_dict = dict()

def add_image(label, image_vector):
    vec = np.array(image_vector)
    if label in image_dict:
        image_dict[label] += vec
    else:
        image_dict[label] = vec
    return image_dict

label_dd = defaultdict(int)
def count_label(data):
    for d in data:
        label_dd[d[0]] += 1
    return label_dd

def plot_digits(X, Y, Z, size_x, size_y, counter, title):
    plt.subplot(size_x, size_y, counter)
    plt.title(title)
    plt.xlim(0,27)
    plt.ylim(0,27)
    plt.pcolor(X, Y, Z)
    plt.gray()
    plt.tick_params(labelbottom="off")
    plt.tick_params(labelleft="off")

まずは代表値$\hat{y}_i$を作ってそれをイメージ表示してみます。

size = 28
raw_data= np.loadtxt('train_master.csv',delimiter=',',skiprows=1)

# draw digit images
plt.figure(figsize=(11, 6))

# data aggregation
for i in range(len(raw_data)):
    add_image(raw_data[i,0],raw_data[i,1:785])

count_dict = count_label(raw_data)

standardized_digit_dict = dict()   # 代表値を格納する辞書オブジェクト
count = 0
for key in image_dict.keys(): 
    count += 1
    X, Y = np.meshgrid(range(size),range(size))
    num = label_dd[key]
    Z = image_dict[key].reshape(size,size)/num
    Z = Z[::-1,:]
    standardized_digit_dict[int(key)] = Z
    plot_digits(X, Y, standardized_digit_dict[int(key)], 2, 5, count, "")

plt.show()

前回、個別のデータをイメージ化して表示した際はとても数字と思えないものもありましたが、多数のデータを重ね合わせて平均をとると綺麗な数字が浮かび上がりますね。これを各クラスの代表値とし、これと識別対象データと比較していくことになります。

###識別の実行：まずは１つお試し###
いよいよ識別の実行です。まずはイメージをつかむために１つの識別対象データと、各クラスの代表値との距離がどのようになるかを見ていきたいと思います。識別対象データはKaggleよりダウンロードしてきます。Dataページのtest.csvを使います。ちょっと数が多いので最初の200個を抽出したデータを準備しています(test_small.csv)

test_data= np.loadtxt('test_small.csv',delimiter=',',skiprows=1)

# compare 1 tested digit vs average digits with norm 
plt.figure(figsize=(10, 9))

for i in range(1):    # 最初の１つだけ試してみる
    result_dict = defaultdict(float)
    
    X, Y = np.meshgrid(range(size),range(size))
    Z = test_data[i].reshape(size,size)
    Z = Z[::-1,:]
    flat_Z = Z.flatten()
    plot_digits(X, Y, Z, 3, 4, 1, "tested")
    
    count = 0
    for key in standardized_digit_dict.keys(): 
        count += 1
        X1 = standardized_digit_dict[key]
        flat_X1 = standardized_digit_dict[key].flatten()
        norm = np.linalg.norm(flat_X1 - flat_Z)   # 各代表値と識別対象データとの距離の導出
        plot_digits(X, Y, X1, 3, 4, (1+count), "d=%.3f"% norm)

plt.show()

識別対象データは"２"ですが、結果はどうでしょう？
各画像の上に距離が表示されています。この数字を見てみると、"２"の上にあるd=1870.936が一番小さいですね！識別成功です！

###識別の実行：200のデータの識別結果###

それでは200個のデータを識別して、その精度を見てみましょう。

# recognize digits
plt.figure(figsize=(15, 130))

for i in range(len(test_data)):
    result_dict = defaultdict(float)
    
    X, Y = np.meshgrid(range(size),range(size))
    tested = test_data[i].reshape(size,size)
    tested = tested[::-1,:]
    flat_tested = tested.flatten()
    
    norm_list=[]
    count = 0
    for key in standardized_digit_dict.keys(): 
        count += 1
        sdd = standardized_digit_dict[key]
        flat_sdd = sdd.flatten()
        norm = np.linalg.norm(flat_sdd - flat_tested)
        norm_list.append((key, norm))
    
    norm_list = np.array(norm_list)
    min_result = norm_list[np.argmin(norm_list[:,1])]
    
    plot_digits(X, Y, tested, 40, 5, i+1, "l=%d, n=%d" % (min_result[0], min_result[1]))
    
plt.show()

200個の識別対象データをこの識別機にかけてみましたが、正解率80%(160/200)とまずますの結果でした！ 平均値との距離を測るだけという割と簡易な手法の割には良い結果なのではないでしょうか。実際の詳細データは下記の図をご覧ください。

識別できなかったケースを分析してみると、特に4と9の識別が難しく6個の識別エラーが出ています。
その次に1-7, 1-8, 3-5, 3-8, 3-9, 8-9がそれぞれ３つのエラーとなっています。やはり見た目も多少似ている数字同士ですね。

識別エラーサマリー

combination of label	count
4-9	6
1-7	3
1-8	3
3-5	3
3-8	3
3-9	3
8-9	3
2-3	2
4-6	2
0-2	1
0-3	1
0-4	1
0-5	1
0-8	1
1-2	1
1-3	1
1-5	1
2-7	1
2-8	1
4-7	1
5-9	1

テンプレートマッチング法の概要

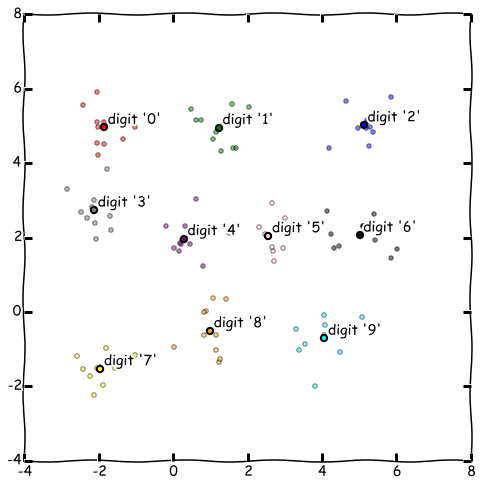
最後にテンプレートマッチング法の概要について少し触れたいと思います。今回の数字データは28x28の784次元データと次元数が高いのでグラフ化できないのですが、イメージをつけるため、2次元だと思って説明します。下記の散布図をみてください。各数字クラスごとのデータが色で見分けがつくようになっていて、データが散らばっている形となっています。これが教師データ一式のイメージです。これを代表値として平均したものをとります。グラフ上、少し大きめの点で表されているのが代表値です。

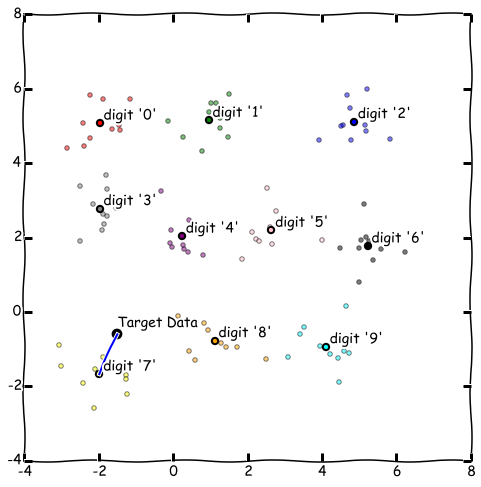
例えば下記の黒い点を識別対象データとすると、一番近い代表値はクラス"７"の代表値なので、この識別対象データをクラス"７"と識別します。これが今回使用したテンプレートマッチング法です。