Go to Qiita Advent Calendar 2024 Top
LoginSignup
276
225

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@Hatomugi

次元削減手法（まとめと実装）PCA, LSI(SVD), LDA, ICA, PLIS

Last updated at Posted at 2019-04-03

##はじめに##
この記事では次元削減法のまとめを載せてます。まとめ要素を強めたかったので詳細な数式等は載せていません。毎回の終わりにもっと詳しいことが書かれている参考文献等を載せているのでご自由に閲覧してください。また間違え等があった場合は下のコメント欄か編集リクエストで教えて頂けると有難いです。

##目次##

  1. PCA (主成分分析)
  2. LSA(SDA) (潜在意味解析 (特異値分解))
  3. LDA (線形判別分析)
  4. ICA (独立成分分析)

##PCA (主成分分析)##

###WHAT:###
PCAとはWikipediaによると、「主成分分析（しゅせいぶんぶんせき、英: principal component analysis; PCA）とは、相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法[1]。データの次元を削減するために用いられる。主成分を与える変換は、第一主成分の分散を最大化し、続く主成分はそれまでに決定した主成分と直交するという拘束条件の下で分散を最大化するようにして選ばれる。」

(#^.^#)？

ということで説明していきます。

抽象的に言ってしまうと「元の情報を出来るだけ失わないようにコアな成分を抽出する次元削減法」のことです。

インプット → 相関のある多数の変数
アウトプット → 相関のない少数の変数
　　　　　　 → 元の情報を最も良く表している (数学的には元のデータの分散を)

相関があるとはx1=3*x2のような線形的な関係があるか否かです。

滅茶苦茶分かりやすいスライドを2つ載せておきます。実際にこちらを見た方が理解するには早いと思います。

https://statistics.co.jp/reference/software_R/statR_9_principal.pdf
https://www.slideshare.net/katsuhiromorishita/ss-97377995

###HOW：###
三次元　→　二次元の場合

1.分散を最大化できる第一主成分の軸を決める。（ここでいう分散を最大化するとは、軸に点を投射したときに各々の点の距離が最大化していることを指す。なぜ分散を最大化するかというとそれだけ元の情報を再現できているからである。）

Untitled (5).png

上の図ではX軸を第一主成分とするのが最も有効と言える。ただし軸は空間上に何本でも引けるので上図のようにXとYの軸からしか選べないということはない。（上の図は説明のために投射する軸を簡略化した）

2.第一主成分の軸を見つけた後は、二番目に分散を最大化できる（第一と直行する）第二主成分の軸を決める。なぜ直行するようにするかというとその方が元の情報を最も保てるし表せるから。

3.三次元の点を二次元の点へ数式を使って変換する。
例えば (x1, x2, x3)を三次元にある一つの点の座標と置き、(y1, y2)を変換後の二次元内の点とする。

y_1 = h_{11}x_1 + h_{21}x_2 + h_{31}x_3 \\
y_2 = h_{12}x_1 + h_{22}x_2 + h_{32}x_3

と言える。ちなみにh21は第一軸の2番目という意味。

寄与率
寄与率とは第i主成分が元のデータをどれだけ表しているかを指す割合である。
これは第i主成分がデータ全体のデータの散らばり具合をどれくらいカバーしているかとも言える。

総分散 = \sum{l_i} \\
第i成分の寄与率 = \frac{l_i}{総分散}

####累積寄与率####
主にデータの何パーセントを成分が表せているか確認するために使う。例えばデータの95%以上を再現している成分を生成したい場合は、「第３主成分までで累積寄与率が80%、第４主成分で95%だから第４主成分までを選ぼう」というような見方ができる。

第i成分までの寄与率 = \frac{l_1+l_2+...+l_n}{総分散}

####主成分得点####
主成分得点とは第i主成分に実際のデータを当てはめて求められた数値のこと。例えば3次元からデータのx1,x2,x3を当てはめて+や-に関係なく大きな数字が出た場合、その第i主成分への関連が高いことが分かる。

主成分得点 = h_{i1}x_1+h_{i2}x_2+...+h_(ip)x_p

###WHY:###

  1. 次元削減をすることでデータの可視化が容易。五次元のデータは見にくいが、二次元のデータ(x,y)はわかりやすい。

  2. 計算コストが高すぎるから。(300次元を指している)300個の変数(x1,x2,x3...x300)と(30次元を指している)30個(x1,x2...x30)の変数があって、どちらもほぼ同じ結果(y)を表現できるなら、30次元の方、つまり変数30個の方を選んだ方が良い。

  3. The curse of dimentionality (次元の呪い)を避けるため。(直訳したら厨二っぽくなってしまいました。。。)次元の呪いとは次元が増えるごとにデータが必要になることを指します。例えば特徴量が10個あり訓練データが100個あったとします。そこで特徴量を100まで増やしました。このとき元の訓練データが100個のままだと過学習を起こすことは容易に想像ができます。これが次元の呪いです。次元を増やすとそれだけデータが必要になるのです。これを避けるために次元削減をする必要があります。

###実装###

公式参照

import numpy as np
from sklearn.decomposition import PCA
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

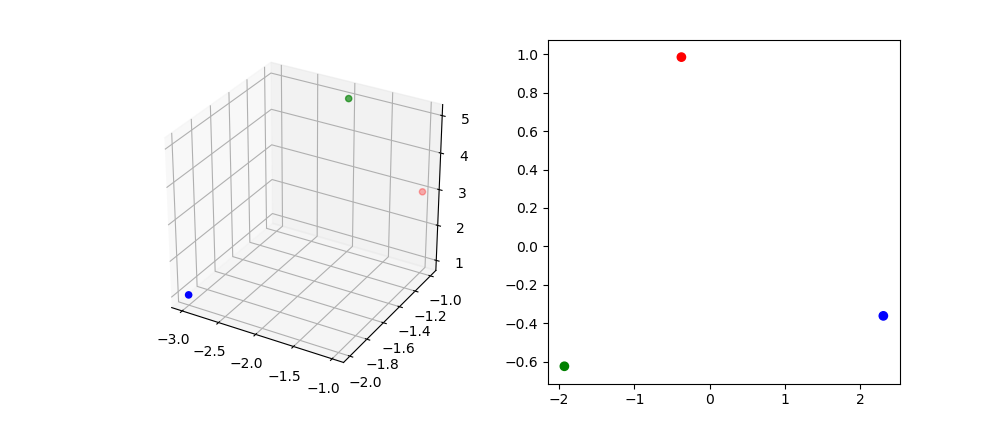
X = np.array([[-1, -1, 3], [-2, -1, 5], [-3, -2, 1]])
pca = PCA(n_components=2)
#モデルのパラメータをfitして取得しPCAオブジェクトへ格納
pca.fit(X)

print('Variance ratio: ' + str(pca.explained_variance_ratio_))
print('Singular values: ' + str(pca.singular_values_))

#fitで取得したパラメータを参考にXを変換する
pca_X = pca.transform(X)
print('Values after PCA: ' + str(pca_X))

結果： Variance ratioが分散の比率。

Variance ratio: [ 0.86039258  0.13960742]
Singular values: [ 3.02944234  1.22030562]
Values after PCA: [[-0.37585859  0.98480528]
                   [-1.92933502 -0.62352025]
                   [ 2.30519361 -0.36128502]]

可視化


fig = plt.figure(figsize=(10,10))

ax1 = fig.add_subplot(221, projection='3d')
ax2 = fig.add_subplot(222)

color = ['red','green','blue']

ax1.scatter3D(X[:,0],X[:,1],X[:,2], color=color)
ax2.scatter(pca_X[:,0], pca_X[:,1], color=color)

plt.show()

3Xh0QXmTRYpLaKf1554090558_1554090576.png

3次元から２次元へ移行しているのが分かります。

###WHERE:###
基本、PCAは使い処が多い。後ほど解説するICAのように特段独立した要素を取り出したいというわけではない場合はPCAを使うことが殆どな印象。例として挙げれば株式マーケットで、投資時に注意するものが何十個もある場合、PCAで重要な要素だけを取り出して数個までに圧縮することでリスク管理がしやすくなる。他にもニューロサイエンスなどで使われるらしい。Wikipedia参照

###合わせて読むと理解が深まるかも+参考文献###

https://qiita.com/NoriakiOshita/items/460247bb57c22973a5f0
https://ja.wikipedia.org/wiki/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90

##LSA(潜在意味解析) or Truncated SVD##

LSAとはSVDを使った次元削減法です。なのでSVDを解説することで大方のアルゴリズムは理解できます。

###SVD(特異値分解)###

####WHAT:####
Wikipediaによると「特異値分解（とくいちぶんかい、英: singular value decomposition; SVD）とは、線形代数学における、複素数あるいは実数を成分とする行列に対する行列分解の一手法である。」です。

(^○^)？

抽象的に言ってしまうと「複数の要素から成る成分を分解して特徴を捉えた小さな要素に分解する」。因数分解みたいなものですね。気を付けたいことはSVDはあくまでも特異値への分解であって、次元削減にフォーカスを当てているわけではありません。

インプット → 複数の要素から成る成分
アウトプット → 特徴を捉えた純粋な要素3つ(その内の一つは特異値と呼ばれるもので、対応する行列（概念）の強度（重要度）を表している）詳しくは下で。

####WHY:####
基本、PCAと一緒。PCAの求め方は2つあって、そのうちの一つはSVDを使っている。詳しくはこちらへまたはこちらへ（英語）

ちなみにsklearnのPCAはSVDを使っているようです。

####HOW:####

A_{[m, n]}=U_{[m, r]}Σ_{[r, r]}{V^T_{[n, r]}}

Aはインプットする行列。
Uを直行行列、Σは対角行列です。
すると、

A = (\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n)
\begin{pmatrix}
\sigma_1 &          &        &          \\
         & \sigma_2 &        &          \\
         &          & \ddots &          \\
         &          &        & \sigma_n
\end{pmatrix}
\begin{pmatrix}
\boldsymbol{v}_1^{\mathrm{T}} \\
\boldsymbol{v}_2^{\mathrm{T}} \\
\vdots \\
\boldsymbol{v}_n^{\mathrm{T}}
\end{pmatrix}

このように分解できます。ここから数式コピー

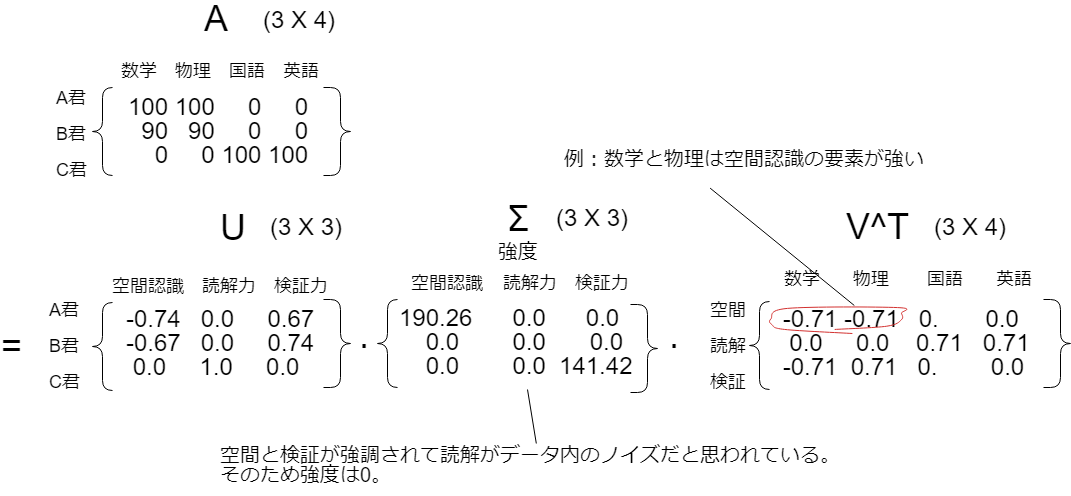
主にUはAから抽出したコンセプト、概念のようなものです。そしてそれを特異値であるΣがその概念がどれほど重要なのか（強いのか）を表しています。

例を使って説明します。ここに理系のA君とB君、文系のC君が居たとして、それぞれの得意教科からどの能力が高いかを抽出しています。（実際にはどの能力が強いかなどは考えられていません。筆者が説明のために勝手に付けています。）

Untitled (3).png

Uのところが所謂概念のような特徴（空間認識力、読解力、検証力）で、Σ（強度、重要度）が190や141等と記入されています。上の図は実際に下の実装欄で得た結果を貼っています。

###LSAに戻る###

さあこれでSVD(特異値分解)は理解できましたが、これがどのように次元削減に役立つのでしょうか。結局分解したのは良いですが、行列が3つになったし次元も殆ど変わってないし寧ろ計算コストが大きくなったように思えます。

しかし勿論これで終わりではなく、次元削減法を組み合わせることで初めて有力になるのがSVDです。次元削減法は二つほどあります。一つは先ほどちょっと触れたSVDを使ったPCAです。PCAは実はSVDを経由しています(sklearnのPCAモジュールはSVDを使っている)。そしてもう一つの方法として、今回メインで話しているLSAです。LSAは別名Truncated SVDとも呼ばれています。Truncatedというのは「切り捨てる」という意味です。それでは何を切り捨てるのかというと特異値を切り捨てます。例えば単純に「特異値が10以下の場合その特異値を切り捨てる」ということができます。切り捨てるというより、実際にはある一定の基準を下回る特異値を0にして、対応する計算の部分を捨てます。これにより計算コストを低く抑えながら、元のAをUΣV^Tでできる限り再現できます。
数式に表すと以下のようになります。dからKの次元へ削減したAkは元のAdに近似しています。

A_d \simeq A_k = U_kΣ_kV^T_k

###実装:###
上で述べた例をここで実装します。

1.SVDで分解する
2.Truncated SVDを使って分解した後に次元を削減する。

1.SVDで分解する

import numpy as np
from scipy.linalg import svd

np.set_printoptions(suppress=True)

# shape=(生徒の数, 教科の数)
A = np.array([[100,100,0,0],[90,90,0,0],[0,0,100,100]])
print(A)

# SVD
U, s, VT = svd(A)
print("This is U: " + str(U))
print("This is s: " + str(s))
print("This is V^T: " + str(VT))

###結果###

[[100 100   0   0]
 [ 90  90   0   0]
 [  0   0 100 100]]

This is U: [[-0.74329415  0.         -0.66896473]
            [-0.66896473  0.          0.74329415]
            [ 0.          1.          0.        ]]

This is s: [ 190.2629759   141.42135624    0.     ]

This is V^T: [[-0.70710678 -0.70710678  0.          0.        ]
              [ 0.          0.          0.70710678  0.70710678]
              [-0.70710678  0.70710678  0.          0.        ]]

Sのところは自動で昇順になっているので実際には[190, 0, 141]だと思われます。

2.Truncated SVDを使って分解した後に次元を削減する。

import numpy as np
from sklearn.decomposition import TruncatedSVD

np.set_printoptions(suppress=True)

A = np.array([[100,100,0,0],[90,90,0,0],[0,0,100,100]])
print("Before: " + str(A))

# SVD
svd = TruncatedSVD(n_components=2, n_iter=7, random_state=42)
svd.fit(A)

X = svd.transform(A)

print("This is matrix after dimentionality reduction: " + str(X))

結果

Before: [[100 100   0   0]
         [ 90  90   0   0]
         [  0   0 100 100]]

This is matrix after dimentionality reduction:
 [[ 141.42135624    0.        ]
  [ 127.27922061    0.        ]
  [  -0.          141.42135624]]

n_componentを2に絞ると、数学力が左のコラムでA君B君のスコアが高く、国語力が右のコラムでC君のスコアが高いというように綺麗にまとめられたのが確認できます。

###WHERE:###
LSAはNLPでよく使われる。
検索エンジンやレコメンドエンジンなどの情報検索の分野
元の行列をユーザーとその性質などに置き換えることもできるので、ECサイトにおいてある一定の性質を持っている顧客へのレコメンド機能も付けることができる。

###合わせて読むと理解が深まるかも+参考文献###
LSI https://mieruca-ai.com/ai/lsa-lsi-svd/
SVD（数式を使って説明）英語：https://math.berkeley.edu/~hutching/teach/54-2017/svd-notes.pdf
SVDとPCAの関連性: https://qiita.com/horiem/items/71380db4b659fb9307b4

##LDA(線形判別分析)##
###WHAT:###
Wikipediaによると「判別分析（はんべつぶんせき、英: discriminant analysis）は、事前に与えられているデータが異なるグループに分かれる場合、新しいデータが得られた際に、どちらのグループに入るのかを判別するための基準（判別関数[1]）を得るための正規分布を前提とした分類の手法。英語では線形判別分析[2]をLDA、二次判別分析[3]をQDA、混合判別分析[4]をMDAと略す。」

抽象的に一言でいえばLDAとは「次元削減をするが、クラス間の分散を最大にしクラス内の分散を最小にする軸を使うことで分類を容易にする次元削減法又はモデル」のことです。PCAの分類フォーカス版という感じでしょうか。

ちなみにLDAは単に次元削減法として使用することもできますし、LDAで次元削減をした後にそのままLDA自体をモデルとして分類問題を解くこともできます。

判別分析 → クラス間の分散を最大化する。
→ クラス内の(点の)分散を最小化する。
→ 教師あり

インプット → 事前に与えられるデータ
アウトプット → 次元削減された分類がしやすいデータ

###WHY:###
1.ロジスティック回帰はデータ数が少ないときに不安定であるため。また多クラス分類に向かないためLDAが使われることが多い。

###HOW:###
基本的には「クラス間の分散を最大にしクラス内の分類を最小にする軸」を探します。その後はPCAと同じ流れです。

クラス間の分類を最大にし、クラス内の分類を最小にするとは数式で表せば下記の式を最適化することです。sを分散、μを中間点とします。

\frac{(μ_1-μ_2)^2}{(s_1^2+s_2^2)}

Untitled (4).png

PCAの軸選びは情報を出来る限り保つために点の分散を最大にするように軸を選んでいましたが、LDAの場合はクラス内の分散を最小にする（まとめる）、かつクラス間の分散は最大にする（分けやすくする）ように軸を選びます。

###実装###
実装に向けて注意することはデータセットが正規分布に従っていることです。結構な点が正規分布に従わない場合、上の例で説明したy軸のような軸で溢れ、LDAは良い軸を見つけられません。よってデータはLDAを通る前に正規化されている必要があります。

また先ほども述べましたが、LDAは単に次元削減法としても実装できますし、LDAで次元削減した後にLDA事態を分類するモデルとすることもできます。

下記の実装では
1.LDAで次元削減し、LDAで分類
2.LDAで次元削減し、lightgbmで分類
をそれぞれ実装します。

1.LDAで次元削減し、LDAで分類
実験として、平均=0と平均=2の二つの違う正規分布からランダムに取り出した数字を混ぜて使います。
平均=0のラベルを0とし、平均=2のラベルを1とします。

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score
from statistics import mean

SIZE = 1000
np.random.RandomState(seed=0)
np.set_printoptions(suppress=True)

#平均３と平均０の正規分布からランダムにSIZE分数字を取り出す
class_1 = np.random.normal(loc=3, size=SIZE)
class_2 = np.random.normal(loc=0, size=SIZE)

# print(class_1)
# print(class_2)

fig, ax = plt.subplots(1,1, figsize=(8,8))

ax1 = sns.distplot(class_1)
ax1 = sns.distplot(class_2)

plt.show()

qiita_lda.png

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score
from statistics import mean
from sklearn.model_selection import train_test_split

SIZE = 1000
np.random.RandomState(seed=0)
np.set_printoptions(suppress=True)

X_1 = pd.DataFrame(np.random.normal(loc=2, size=(SIZE, 3)), columns=['a', 'b', 'c'])
data_1 = pd.concat([X_1, pd.DataFrame(np.zeros((SIZE, 1), dtype=int), columns=['target'])], axis=1)

X_2 = pd.DataFrame(np.random.normal(loc=0, size=(SIZE, 3)), columns=['a', 'b', 'c'])
data_2 = pd.concat([X_2, pd.DataFrame(np.ones((SIZE, 1), dtype=int), columns=['target'])], axis=1)

data = pd.concat([data_1, data_2], ignore_index=True)

#データをシャッフル
data = data.sample(frac=1, random_state=0).reset_index(drop=True)

#XとtargetのYを分ける
X = data.drop(['target'], axis=1)
Y = data['target']

#訓練データと検証用データを0.7:0.3の割合で分ける
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.30, random_state=42)

#モデル生成
clf = LinearDiscriminantAnalysis()
#predictするのに必要なパラメータを訓練して生成する
clf.fit(X_train, Y_train)

#テストする
predicted = clf.predict(X_test)
score = accuracy_score(predicted, Y_test)

print('Accuracy: ' + str(score))

結果

Accuracy: 0.958333333333

2.LDAで次元削減し、lightgbmで分類

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score
from statistics import mean
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
import lightgbm as lgb

SIZE = 1000
np.random.RandomState(seed=0)
np.set_printoptions(suppress=True)

X_1 = pd.DataFrame(np.random.normal(loc=2, size=(SIZE, 3)), columns=['a', 'b', 'c'])
data_1 = pd.concat([X_1, pd.DataFrame(np.zeros((SIZE, 1), dtype=int), columns=['target'])], axis=1)

X_2 = pd.DataFrame(np.random.normal(loc=0, size=(SIZE, 3)), columns=['a', 'b', 'c'])
data_2 = pd.concat([X_2, pd.DataFrame(np.ones((SIZE, 1), dtype=int), columns=['target'])], axis=1)

data = pd.concat([data_1, data_2], ignore_index=True)

#データをシャッフル
data = data.sample(frac=1, random_state=0).reset_index(drop=True)

#XとtargetのYを分ける
X = data.drop(['target'], axis=1)
Y = data['target']

#モデル生成
clf = LinearDiscriminantAnalysis()
#predictするのに必要なパラメータを訓練して生成する
clf.fit(X, Y)

#LDAにデータを通して変換する
X = clf.transform(X)

params = {
	'objective':'binary', 
	'max_depth':-1,
	'n_estimators':200,
	'learning_rate':0.1,
	'colsample_bytree':0.3,
	'num_leaves':8,
	'metric':'auc',
	'n_jobs':-1
}

folds = KFold(n_splits=5, shuffle=False, random_state=0)

print('Light GBM Model')

acc = list()

for fold_, (trn_idx, val_idx) in enumerate(folds.split(X)):
	print("Fold {}: ".format(fold_+1))
	clf = lgb.LGBMClassifier(**params)
	clf.fit(X[trn_idx], Y[trn_idx], eval_set=[(X[val_idx], Y[val_idx])], verbose=0, early_stopping_rounds=500)

	y_pred_test = clf.predict_proba(X[val_idx])
	y_pred_k = np.argmax(y_pred_test, axis=1)
	acc.append(accuracy_score(Y[val_idx], y_pred_k))

print(mean(acc))

結果

Accuracy: 0.955

データが単純だというのもあるが大体一緒の結果でした。ただしLDAの本領はロジスティック回帰と比べたときに多クラス分類が容易だということなので、そこはポイントだと言えます。ここでは説明のために2クラスだけ使いました。ちなみに指摘し忘れましたが、gbm様は安定ですね。

###WHERE:###
分類問題なら基本どこでも。ただしデータは出来るだけ正規分布に従っている必要がある。ロジスティック回帰との利点や欠点を考えてやる必要がありそう。

###合わせて読むと理解が深まるかも+参考文献###
ステップがわかりやすい（英語）
https://www.slideshare.net/JaclynKokx/introduction-to-linear-discriminant-analysis
https://www.youtube.com/watch?v=azXCzI57Yfc

##ICA(独立主成分分析)##
###WHAT:###
Wikipediaによると「独立成分分析（どくりつせいぶんぶんせき、英: independent component analysis、ICA）は、多変量の信号を複数の加法的な成分に分離するための計算手法である。各成分は、ガウス的でない信号で相互に統計的独立なものを想定する」

(ﾟ∀ﾟ)？

抽象的に言ってしまえば「多くの変数から成る変数を少数（又は同じ数の）正規分布に従わないお互いに独立した成分に次元削減する手法」のこと。

因数分解すると以下になります。

ちなみに多変量とは「多くの変数から成る」という意味です。

インプット　→ 多くの変数から成る成分

アウトプット→ 複数の成分
　　　　　　→ それぞれの成分は正規分布に従わない。
　　　　　　→ それぞれの成分はお互いに独立している。

注意すべきはPCAを通した後の結果はお互いに無相関な成分なのに対し、ICAを通した後の結果はお互いに独立な成分であることです。

よって次の用語の意味の違いを知っておく必要があります。

無相関 - 線形的な関係は無いが、非線形的な関係はあるかもしれない。
独立 - 線形的な関係が無く、非線形的な関係も無い。

例として「線形的な関係が無いが、非線形的な関係はある」概念を再現して無相関になるか否かを確かめてみます。　yをx^2としすることで「線形的な関係は無いが、非線形的な関係はある」を体現します。

import numpy as np

x = np.array([-5,-4,-2,-1,0,1,2,3,4,5])
y = np.array([25,16,9,4,1,0,1,4,9,16,25])

np.correlate(x,y)

結果

0.0

答えは無相関です。これは（非線形的な関係があっても）線形的な関係は無いから無相関と判断しています。

###WHY:###
PCAに述べた時のようにデータの可視化のため、計算コストを抑えるため、The curse of dimentionality対策のため等が挙げられますが、PCAと比べて次元削減をしながら独立した要素を抽出したいとき(又は独立した要素の抽出を仮定しているとき)はICAが必要となりそうです。例えば下記のHOW:で述べているのが一例です。

###HOW:###
それでは有名なカクテルパーティー問題を例に説明します。（この有名な論文を参照）

カクテルパーティー問題の元ネタはカクテルパーティー効果と言われるものです。「これはカクテルパーティーのように、沢山の人がそれぞれに雑談しているなかでも、自分が興味のある人の会話、自分の名前などは、自然と聞き取ることができる。」(wikipedia引用）です。

これは正に多くの変数から成る成分(全てが混ざった雑音)から少数の成分(興味のある人の声)を抽出しています。ちなみに独立もしています。なぜなら人の声は他人に影響されない独立した変数だからです。

ではこれを数式で表してみましょう。

x_1=a_{11}s_1^i+a_{12}s_2^i \\
x_2=a_{21}s_1^i+a_{22}s_2^i

それぞれのsを信号（声）とし、iを時間経過、xをマイクロフォンが拾った音の振幅とします。
グラフィック的に表現すると以下になります。s1とs2の各々の声の振幅を以下と仮定します。

ica1.png

そしてこれが、２つのマイクロフォン（x1とx2）で拾った振幅です。雑音が入っているので少し乱れているのがわかります。

ica2.png
出典: Independent Component Analysis: Algorithms and Applications

問題は最初の2人の音の振幅を、2番目のマイクロフォンで拾った振幅から計算して出すことです。

行列の式で表すと以下となります。

X^i=AS^i

Aを未知の可逆、正方、混合行列とし、XとSをランダムな数字から決めたn次元の行列とします。ちなみにSはお互いに独立します。
やりたいことはマイクロフォンで拾った音(X)と未知の行列Aを使って、純粋に二人の声S1とS2を求めることです。

そこで以下のケースが考えられます。

  1. Aが既に分かっている。
    この場合はA^-1を取れば解決します。もしICAのあとの独立成分が変数の数より少ないのならAは低次元かを行う行列です。
S^i=X^iA^{-1}
  1. Aが分からない。（殆どのケース）
    この場合はAを試していくしかありません。

Aを試していくメジャーな方法は２つあって、そのうちの一つは如何に正規分布と離れているかというものです。詳しいことは投げやりですがこちらへ。
33ページにエントロピーを使った求め方やネゲントロピーを使った予測方法などが載ってます。また実装で使うFastICAはネゲントロピーを使って正規分布と離れているかを推測するアルゴリズムのようです。筆者はエントロピーを物理でしか聞いたことがない人なので勉強中です。

この後は毎回のステップでエラーを勾配降下法などで成分の基底が非正規分布になるようにするだけです。

よって再三ですが、以下のようになります。

インプット　→ 多くの変数から成る成分

アウトプット→ 複数の成分
　　　　　　→ それぞれの成分は正規分布に従わない。
　　　　　　→ それぞれの成分はお互いに独立している。

以下はPCAとICAを2次元に圧縮した基底の違いです。基底とは互いに独立したベクトルで、ベクトル空間内の各々の点を表すことができるベクトルです。PCAの基底は分散を最大化するために直交していることがわかります。またICAの基底は独立できる方向を探しているので直交していません。また点が基底に沿っていますが、これは基底自体が独立したベクトルだからです。

出典: Applications of ICA

slide_2.jpg

###実装###
まず初めにsizeを(3, 3)、１次元に３つの要素を置いてそれを３次元分用意します。
そしてそこから独立した成分を抽出します。

import numpy as np
from matplotlib import pyplot as plt
from sklearn.decomposition import FastICA
import seaborn as sns

# array = np.random.normal(size=(1000,5))
np.random.seed(0)
X = np.random.uniform(low=0, high=10, size=(5, 10))

print('Before ICA: ' + str(X))
print('Shape' + str(X.shape))

ica = FastICA(n_components=3)
S = ica.fit_transform(X)

print('After ICA: ' + str(S))
print('Shape' + str(S.shape))

###結果###

Before ICA:
[[ 5.48813504  7.15189366  6.02763376  5.44883183  4.23654799  6.45894113
   4.37587211  8.91773001  9.63662761  3.83441519]
 [ 7.91725038  5.2889492   5.68044561  9.25596638  0.71036058  0.871293
   0.20218397  8.32619846  7.78156751  8.70012148]
 [ 9.78618342  7.99158564  4.61479362  7.80529176  1.18274426  6.39921021
   1.43353287  9.44668917  5.21848322  4.1466194 ]
 [ 2.64555612  7.74233689  4.56150332  5.68433949  0.187898    6.17635497
   6.12095723  6.16933997  9.43748079  6.81820299]
 [ 3.59507901  4.37031954  6.97631196  0.60225472  6.66766715  6.7063787
   2.10382561  1.28926298  3.15428351  3.63710771]]
Shape: (5, 10)

After ICA:
[[-0.47260168  0.13058151 -0.10310685]
 [ 0.49314232 -0.50897592  0.50581338]
 [-0.31494494 -0.54523519 -0.4594546 ]
 [-0.29491268  0.45612478  0.53867448]
 [ 0.58931698  0.46750482 -0.48192642]]

Shape: (5, 3)

10個あった要素(Components)がICAと通した後は3個に減っているのが分かります。
そしてこの3つはお互いに独立しています。

###WHERE:###
基本的に複数の織り交ざった要素から単一な独立した要素を取り出すときに使えます。例として株価予測などに使えるそうです。
また顔認識にも使えるそうです。

###合わせて読むと理解が深まるかも+参考文献###
https://www.hellocybernetics.tech/entry/2016/05/01/185044
https://datachemeng.com/independentcomponentanalysis/
https://ja.wikipedia.org/wiki/%E7%8B%AC%E7%AB%8B%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
https://danieltakeshi.github.io/2015/01/03/independent-component-analysis-a-gentle-introduction/
https://blog.paperspace.com/dimension-reduction-with-independent-components-analysis/
https://towardsdatascience.com/dimensionality-reduction-ways-and-intuitions-1b5e97592d8e

276
225
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
276
225

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?