この記事ではMATLABで3Dモデルを作ったりレンダリングしたりする簡単な方法について説明します。
MATLABは3Dモデリングのために作られたソフトウェアではないのですが、それなりに3D表示の機能がよくできています。影や映り込みなど複雑な3Dレンダリングができないものの、それでも簡単なシェーディングができて綺麗な画像が作れます。
簡単なサーフェスの作成
MATLABでは3D物体の表面を表現するには基本的に「サーフェス」(surface)と「パッチ」(patch)オブジェクトを使います。
パッチの方は自由度が高いけどちょっと複雑なので、まずはすぐ手軽に作れるサーフェスの方から説明します。
サーフェスを作る関数は沢山ありますが、一番簡単に使えるのはmesh、surf、surface関数を使うことです。どれも同じサーフェスオブジェクトを作るが、既定値が違うだけです。ちゃんと詳しく設定するならどっちも同じになります。
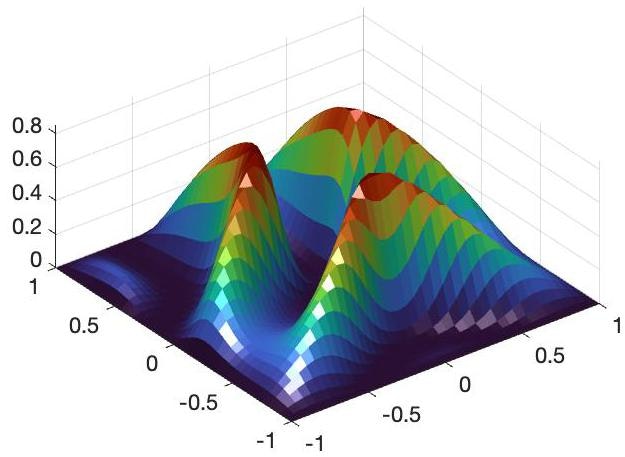
違いについては後で説明しますが、まず一番簡単なmesh関数で例を挙げます。
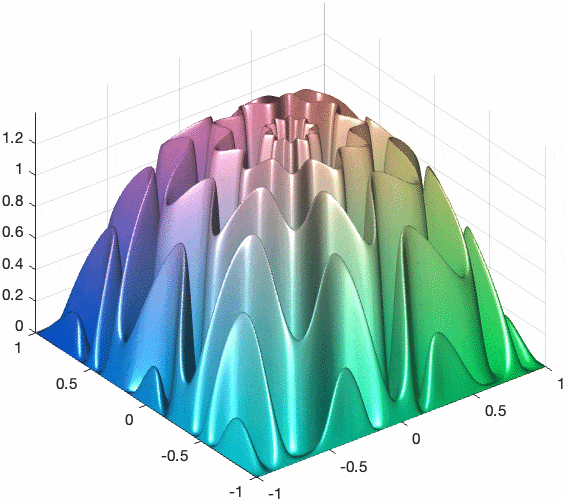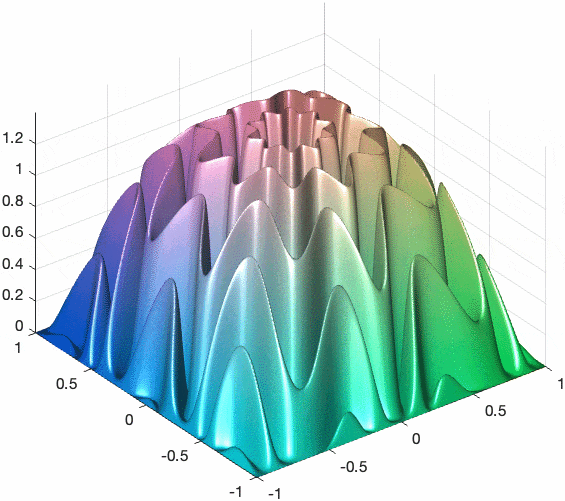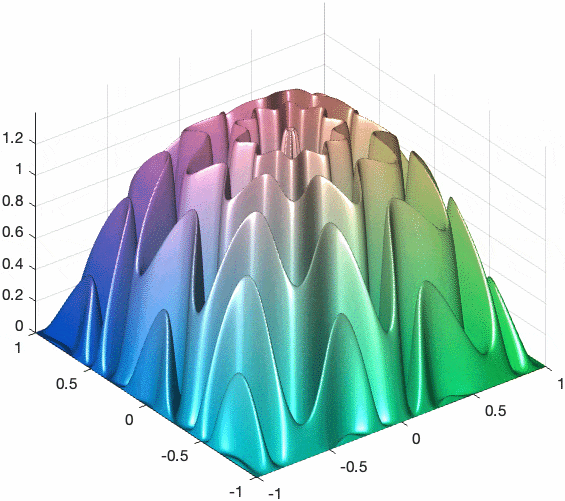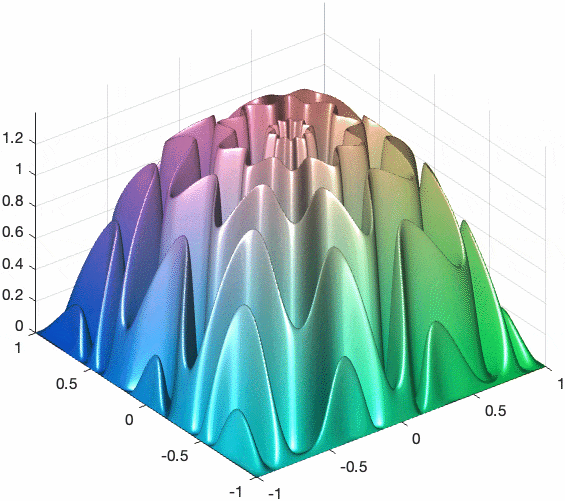
[mx,my] = meshgrid(-1:0.002:1,-1:0.002:1);
mz = (sin(sqrt(mx.^2+my.^2).*(1+cos(atan2(my,mx)*6)*0.3)*2*pi).^2+randn(size(mx))*0.004).*(1-mx.^2).*(1-my.^2);
mesh(mx,my,mz)
light(Position=[-3 -5 8])
axis equal
これだけのコードでこんな3D表面が出来上がりです。
作り方はまずmeshgrid関数でメッシュのx,yの値を準備しておいて、そこからzの値も計算します。そしてx,y,zからサーフェスを作ります。
ただしそれだけではまだ3Dに見えなくて物足りないので、light関数で照明を入れてシェーディングが見えるようにします。
最後にaxis equalでx,y,zの比率を一致させます。そうしないと歪みます。又、axisのところで色々軸に関する設定ができます。例えばaxis offを書いて座標軸を消してサーフェスだけ表示することができます。
表面の色に関しては、ここで自動的にzの値でカラーマップによって塗られます。
colormap関数などで違うカラーマップに変えることで好きな色の配置に変更することができます。
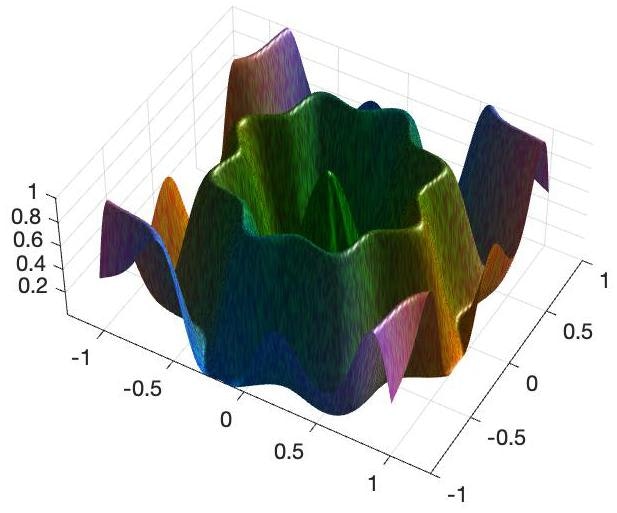
試しにカラーマップを変えて座標軸も非表示にします。
[mx,my] = meshgrid(-1:0.002:1,-1:0.002:1);
mz = sin(sqrt(mx.^2+my.^2).*(1.2+sin(atan2(my,mx)*4)*0.2)*2*pi).^2.*(1-mx.^2).*(1-my.^2);
mesh(mx,my,mz)
colormap sky
light(Position=[-2 -6 3])
axis equal off
zの値とは関係なく自分で色を決めたい場合は4つ目の値を関数に入れます。それは各頂点の色となります。もしm×n×3サイズの配列で入れたらそれはRGB色を指定することになりますが、m×nだったら(zの値の代わり)にカラーマップに使う値となります。
例えばRGBで色を指定してみます。
[mx,my] = meshgrid(-1:0.002:1,-1:0.002:1);
mz = ((cos(sqrt(mx.^2+my.^2).*(1+cos(atan2(my,mx)*5)*0.3)*2*pi).^2)-abs(randn(size(mx))*0.01)).*(1-mx.^2).*(1-my.^2);
mc = cat(3,1-(mx+1)/2,1-(my+1)/2,1-mz);
mesh(mx,my,mz,mc)
light(Position=[-1 -5 3])
axis equal
このように綺麗な3D表面が表示できます。
アニメーションを作る
MATLABでは動画を作る方法が色々あります。例えばexportgraphics関数を使って、変わっていく座標軸を捉えていくのです。
サーフェスはdelete関数で消して新しく作ることで動きを表すこともできますが、そうするよりも既存のサーフェスのx,y,zや色を少しだけ変えることもできます。その方が効率がいいでしょう。
mesh関数で作った時に返り値を受け取ったらそれにサーフェスオブジェクトが入って、そのオブジェクトのXData、YData、ZDataを再設定して形を変えることができます。又、色はCDataで。
ではこの方法で簡単なgifアニメーションを作ります。
[mx,my] = meshgrid(-1:0.002:1,-1:0.002:1);
sf = mesh(mx,my,mx);
light(Position=[-4 -3 1])
axis equal
for i = 0:11
mz = sin(sqrt(mx.^2+my.^2).*(2+cos(atan2(my,mx)*10)*0.3)*2*pi-i/12*pi).^2.*(1-mx.^4).*(1-my.^4);
sf.ZData = mz/max(mz(:))*1.4;
sf.CData = cat(3,mz,1-(my+1)/3,1-(mx+1)/3);
exportgraphics(gcf,'meshanim.gif',Append=~~i,Resolution=100);
end
meshとsurfとsurface
以上の例ではわざと網の間隔を小さく設定したから網はほぼ表面に見えますが、実はmeshをデフォルトでは本物の表面が白いのです。そもそもmeshただの網であり、表面に色が付いているわけではないのです。
こうやって間隔を大きくしたら色が網の線に付いて表面が白いとわかります。
[mx,my] = meshgrid(-1:0.05:1,-1:0.05:1);
mz = ((sin(0.4.*sqrt(mx.^2+my.^2).*(1+sin(atan2(my,mx)*3)*0.6)*2*pi).^4)).*(1-mx.^2).*(1-my.^2);
mesh(mx,my,mz)
colormap turbo
light(Position=[-4 -2 12])
axis equal
もしmeshの代わりにsurfを使ってみたら色が表面に付いて、代わりに線が黒になります。
surf(mx,my,mz)
これがmeshとsurfの違いです。
そしてsurfaceは基本的にsurfと同じようなサーフェスオブジェクトを作るのです。ただしsurfとmeshを使うと視点が自動的に3Dに変えたりグリッドを入れたりするのに対し、surfaceはただサーフェスを作ることです。
試しにsurfの代わりにsurfaceを使うとこうなります。
surface(mx,my,mz)
上からの視点になって、あまり3Dに見えないですね。だから後で視点を変える必要があります。
面と辺の表示の設定
上述の通り、meshとsurf(とsurface)の違いはただ線と表面の表示です。それは既定値が違うからです。
| プロパティ | surf | mesh |
|---|---|---|
| FaceColor | 'flat' |
[1 1 1] |
| FaceLighting | 'flat' |
'none' |
| EdgeColor | [0 0 0] |
'flat' |
| EdgeLighting | 'none' |
'flat' |
逆にこれをちゃんと設定したらどれを使うも同じです。
例えば線が要らないならEdgeColor="none"で非表示することもできます。上述の例でこれに書き換えてもう一度描いてみたらこうなります。
surf(mx,my,mz,EdgeColor="none")
又はLineStyle="none"も同じようにできます。
surf(mx,my,mz,LineStyle="none")
FaceColorは既定値ではflatですが、これはただ面ごとに色を決める単純な表示ですが、不自然に感じますね。
FaceColor="interp"にすること面の中の色が内挿によって計算されて滑らかな漢字になります。
surf(mx,my,mz,EdgeColor="none",FaceColor="interp")
ただしこれだけではまだ不自然です。FaceColor="interp"にしてもそれはただ素の色のことだけで、照明の反射はまだ面ごとに違うままだからです。
照明のシェーディング
照明を面ごとに計算するフラットシェーディングのではなくもっと自然にするにはグーローシェーディングを使うという方法があります。FaceLighting="gouraud"にすることでできます。
surf(mx,my,mz,EdgeColor="none",FaceColor="interp",FaceLighting="gouraud")
又、lightingを使うことで全てのサーフェスやパッチに照明のシェーディングを変更することもできます。
lighting gouraud
こうしたら結果はこうなります。
まだギザギザって感じが残っていますが、メッシュの間隔を細かくすることで解決できます。これだけでもローポリなりによくできると言えるでしょう。又、角に弱いのはグーローシェーディングの欠点としても知られていますね。
ただしグーローシェーディングを使うと当然フラットシェーディングより計算時間が必要なので、使う必要があるかどうかちゃんと考えておいた方がいいです。メッシュを細かくしたらグーローシェーディングでもフラットシェーディングでもあまり違わないはずなので、計算時間が気になったらフラットシェーディングのままでもいいと思います。
眺める角度
meshやsurf関数を使うと視点は自動的に [方位角,仰角]=[-37.5,30]度という眺める角度に設定されますが、好きな角度に設定したい場合簡単にview関数でできます。
[mx,my] = meshgrid(-1:0.004:1,-1:0.004:1);
mz = ((sin(1.6.*sqrt(mx.^2+my.^2).*(1+sin(atan2(my,mx)*16)*0.1)*2*pi).^2))*0.2;
mc = cat(3,mx.^2,my.^2,unifrnd(0.5,0.7,size(mx)));
mesh(mx,my,mz,mc,EdgeColor="none",FaceColor="interp",FaceLighting="gouraud")
light(Position=[0 0 1])
view(180,45)
axis equal
又は、gca関数で座標軸を取得してset関数で.Viewプロパティへ代入することもできます。
set(gca,"View",[45 45])
普段viewを使うと座標軸の他のカメラに関する色んなプロパティの値が自動的に決められますが、もっと細かく設定したい場合は直接設定した方がいいです。
| プロパティ | 意味 | 既定値 |
|---|---|---|
| CameraPosition | カメラが置かれている位置 | [0.5000 0.5000 9.1603] |
| CameraTarget | カメラが向かう位置 | [0.5000 0.5000 0.5000] |
| CameraViewAngle | カメラの視野の角度 | 6.6086 |
| CameraUpVector | カメラの頭上へ向かうベクトル | [0 0 1] |
| Projection | 2次元の画面へ射影する方式 | 'orthographic' |
Projectionはperspective(透視投影)にすることで現実みたいな眺め方に近い形になります。既定値のorthographic(正投影)だと無限大遠い距離から眺めるみたいな感じで遠近感はしません。
set関数で直接Projectionの値を変えることもできますが、camproj関数で設定することもできます。
透視投影にすることでカメラが近づくと見える形が変わっていきます。
[mx,my] = meshgrid(-1:0.01:1,-1:0.01:1);
mz = ((cos(0.8.*sqrt(mx.^2+my.^2).*(1+sin(atan2(my,mx)*8)*0.1)*2*pi).^2));
mc = cat(3,mx.^2,unifrnd(0.3,0.7,size(mx)),my.^2);
mesh(mx,my,mz,mc,EdgeColor="none",FaceColor="interp",FaceLighting="gouraud")
light(Position=[1 1 1])
camproj("perspective") % 又は set(gca,"Projection","perspective")
view(0,90)
axis equal
for i = 0:9
set(gca,CameraPosition=[0 0 6-i*0.5])
pause(0.2)
end
因みにこの表面は横から見たらこんなこうなります。
照明
照明はlight関数で設定できますが、設定できるのは3つしかありません。
| プロパティ | 意味 | 既定値 |
|---|---|---|
| Position | 光源の位置 | [1 0 1] |
| Color | 照明の色 | [1 1 1] |
| Style | 光源の種類 | 'infinite' |
Styleは既定値のinfiniteかlocalにするのです。infiniteだとディレクショナルライトになってたとえどこに光源を置いても無限大距離から照らすようなことになりますが、localにすることでポイントライトになって実際にその位置から照らすことになります。
例えばこの表面と照明。
[mx,my] = meshgrid(-1:0.002:1,-1:0.002:1);
mz = cos(sqrt(mx.^2+my.^2).*(1+sin(atan2(my,mx)*4)*0.2)*4*pi).^4;
mc = cat(3,unifrnd(0.5,0.7,size(mx)),mx.^2,my*0.5+0.5);
mesh(mx,my,mz,mc,EdgeColor="none",FaceColor="interp",FaceLighting="gouraud")
light(Position=[0 0 1.2],Color=[1 0.8 0.5],Style="local")
camproj("perspective")
view(0,90)
axis equal
これがStyle="local"にすることで結果は大きく違います。
light(Position=[0 0 1.2],Color=[1 0.8 0.5],Style="local")
因みにわかりやすくするように光源の位置を示す点を描いて横からみたらこんな感じです。
hold on
scatter3(0,0,1.2,MarkerFaceColor=[0.9 0.9 0.7])
view(0,40)
このように光源が近くに置いてある場合はlocalとinfiniteの違いははっきりとわかりますね。
その他にもlightangle関数を使って照明の角度で設定することもできます。この場合は光源の位置は自動的に決められます。
lightangleは普通に使うとlightと同じように新しい光源を作ることになりますが、既存の光源のオブジェクトを入れることでその光源を移動させることになります。これは照明が変わっていくアニメーションを作る時に便利です。そうでないと元の光源オブジェクトを消してから新しく入れる必要があるから。
使う例。
[mx,my] = meshgrid(-1:0.004:1,-1:0.004:1);
mz = ((sin(1.6.*sqrt(mx.^2+my.^2).*(1+sin(atan2(my,mx)*2)*0.4)*2*pi).^2)).*(1-mx.^4).*(1-my.^4)+0.025*(my+1);
mc = cat(3,1-(mx+1)/2,(my+1)/2,mz);
mesh(mx,my,mz,mc,EdgeColor="none",FaceColor="interp",FaceLighting="gouraud")
axis equal
hikari = light(Color=[1 1 0.5]);
for kakudo = -90:10:0
lightangle(hikari,kakudo,10)
pause(0.2)
end
又はcamlight関数で照明の位置をカメラとの関係で決めることもできます。
透明にする
サーフェスオブジェクトのFaceAlphaの値を設定することで透明にすることができます。既定値は1ですが、0に近いほど見えなくなります。
透明度を変えていくアニメーションを作ってみます。
[mx,my] = meshgrid(-1:0.002:1,-1:0.002:1);
sf = surf(mx,my,zeros(size(mx)),mc,EdgeColor="none");
lightangle(0,40)
axis equal
for i = 0:10
mz = ((cos(sqrt(mx.^2+my.^2)*2*pi+atan2(my,mx)*5+i/2).^2)).*(1-mx.^6).*(1-my.^6);
sf.ZData = mz;
sf.CData = cat(3,(mx+1)/2,1-mz,1-(my+1)/2);
sf.FaceAlpha = 1-i*0.1;
pause(0.2)
end
又、FaceColor="none"にすることで表面を非表示にしてメッシュの線だけ表示することもできます。
[mx,my] = meshgrid(-1:0.05:1,-1:0.05:1);
mz = ((cos(sqrt(mx.^2+my.^2)*pi+atan2(my,mx)).^2)).*(1-mx.^6).*(1-my.^6);
mesh(mx,my,mz,FaceColor="none")
colormap cool
light(Position=[0.5 1 0.2],Color=[1 0.7 0.3])
axis equal
材質
表面の材質を変えることで反射は違うように見えます。既定値でも綺麗に反射するように設定されているのですが、表現したい物体に合うように材質を変えることもできます。
材質に関わるプロパティは5つあります。
- AmbientStrength: 周囲光の強度
- DiffuseStrength: 拡散光の強度
- SpecularStrength: 鏡面反射の強度
- SpecularExponent: 鏡面反射の膨張性
- SpecularColorReflectance: 鏡面反射の色
これはサーフェスオブジェクトを作成する時に他のキーワードと一緒に入れることで設定することもできますが、その他にももし複数のオブジェクトがあったら一気にmaterial関数で設定することもできます。
material関数の使い方は2つあります。1つは[AmbientStrength, DiffuseStrength, SpecularStrength, SpecularExponent, SpecularColorReflectance]の値が入っている配列で設定するのです。そしてもう一つはdefault、shiny、dull、metalを書くのです。それぞれそれらしい材質に値を変更されます。(defaultは既定値と同じ)
| プロパティ | default | shiny | dull | metal |
|---|---|---|---|---|
| AmbientStrength | 0.3 | 0.3 | 0.3 | 0.3 |
| DiffuseStrength | 0.6 | 0.6 | 0.8 | 0.3 |
| SpecularStrength | 0.9 | 0.9 | 0 | 1 |
| SpecularExponent | 10 | 20 | 10 | 25 |
| SpecularColorReflectance | 1 | 1 | 1 | 0.5 |
それぞれの違いを表す例。
[mx,my] = meshgrid(-1:0.005:1,-1:0.005:1);
mz = (sin(mx.^2*pi)+sin(my.^2*pi)-sin(mx.^2*pi).*sin(my.^2*pi)).*(1-mx.^16).*(1-my.^16);
hold on
mat = ["default" "shiny" "dull" "metal"];
for i = 1:4
dx = ceil(i*0.5)*2;
dy = mod(i,2)*2;
text(dx,dy,1,"["+mat(i)+"]",Color=[0.8 0.7 1],HorizontalAlignment="center",FontSize=8)
sf = surf(mx+dx,my+dy,mz,EdgeColor="none",FaceColor="interp",FaceLighting="gouraud");
material(sf,mat(i))
end
colormap copper
light(Position=[-2 -1 1])
axis equal off
view(10,40)
画像を表面に貼る
サーフェスを作成する時にFaceColor="texturemap"にすることで画像を表面の色に使うことができます。
例えばこの画像を球体の表面に貼ることにします。
sarada.jpg
|
[phi,theta] = meshgrid(deg2rad(0:0.2:120),deg2rad(40:0.2:140));
r = 1+randn(size(phi))*0.001;
mx = r.*cos(phi).*sin(theta);
my = r.*sin(phi).*sin(theta);
mz = r.*cos(theta);
mc = imread("sarada.jpg");
wp = surf(mx,my,mz,mc,EdgeColor="none",FaceColor="texturemap");
lighting gouraud
camproj("perspective")
material shiny
view(150,20)
lightangle(180,-10)
lightangle(40,-60)
axis equal
又はwarp関数を使って同じようなことをすることもできますが、既定値の設定はsurfと微妙に違います。
ポリゴン(パッチ)
以上はサーフェスオブジェクトばかり使って説明していたのですが、普段3Dソフトウェアなどではポリゴンを使う方法の方が一般的です。
MATLABは3Dモデリングソフトウェアみたいに使い勝手がいいポリゴンはないが、似ているものとしてパッチというオブジェクトがあります。
使い方は、例えば立方体はこうやって作れます。
ar_v = [-5 -5 -5
5 -5 -5
5 5 -5
-5 5 -5
-5 -5, 5
5 -5 5
5 5 5
-5 5 5];
ar_f = [4 3 2 1
1 2 6 5
2 3 7 6
3 4 8 7
4 1 5 8
5 6 7 8];
ar_c = [0 0 0
1 0 0
0 1 0
0 0 1
1 1 0
1 0 1
0 1 1
1 1 1];
p = patch(Faces=ar_f, ...
Vertices=ar_v, ...
FaceVertexCData=ar_c, ...
FaceColor="interp", ...
FaceLighting="gouraud", ...
FaceAlpha=0.4);
camproj("perspective")
view(140,30)
lightangle(135,60)
axis equal
patch関数で作る時に、Verticesは全部の頂点の位置のx,y,zで、Facesは各面に使う頂点のインデックスで、FaceVertexCDataは頂点の色です。その他のキーワードやプロパティは殆どサーフェスと同じになります。
サーフェスは連続の長方形のメッシュを変形することで表現するのに対し、パッチは頂点と面を指定することで自由にどんな形にすることもできます。
例えばアイスクリームみたいな形を作ります。
[ar_z,ar_theta] = meshgrid(0:0.02:10-0.02,deg2rad(0:0.5:360-0.5));
sx = size(ar_z,1);
sy = size(ar_z,2);
ar_r = 5.*(sin((1-ar_z/10).^0.5*pi/2).^4).*(1+0.2.*abs(sin(ar_z*pi/2+ar_theta)))+randn(sx,sy)*0.01;
ar_x = ar_r.*cos(ar_theta);
ar_y = ar_r.*sin(ar_theta);
ar_v = [ar_x(:) ar_y(:) ar_z(:)
0 0 10];
ar_f1 = reshape( ...
cat(3, ...
(1:sx)' + (0:sx:sx*(sy-1)-1), ...
[2:sx 1]' + (0:sx:sx*(sy-1)-1), ...
[2:sx 1]' + (sx:sx:sx*sy-1), ...
(1:sx)' + (sx:sx:sx*sy-1)), ...
[],4);
ar_f2 = [(sx*(sy-1)+1:sx*sy)' ...
[sx*(sy-1)+2:sx*sy sx*(sy-1)+1]' ...
repmat(sx*sy+1,sx,1) ...
NaN(sx,1)];
ar_f = [ar_f1
ar_f2];
ar_c = [unifrnd(0.5,1,[sx*sy+1 1]) linspace(0.7,1,sx*sy+1)' unifrnd(0.8,0.9,[sx*sy+1 1])];
p = patch(Faces=ar_f, ...
Vertices=ar_v, ...
FaceVertexCData=ar_c, ...
FaceColor="interp", ...
FaceLighting="gouraud", ...
LineStyle="none");
camproj("perspective")
view(0,20)
lightangle(0,70)
axis equal
grid
パッチはサーフェスより想像力が必要であまり扱いが簡単ではないが、上手く使いこなせればどんなに複雑な表現もできます。
これを使って色々3Dモデルを作っていくのが楽しいです。
限界の話
このように綺麗な3DレンダリングができるMATLABですが、当然ながら専用の3Dソフトウェアの代わりに使うのは限界があるでしょう。簡単な3D表現はできますが、現実っぽい画像を作るのはまだ難しいです。
まだできないもっと複雑なことは例えば
- UVマップ
- バンプマッピング
- 影を作る
- レイトレーシング
- 鏡みたいな映り込み
- 透明な表面による屈折
- エリアライト
- サブサーフェス・スキャタリング
などなど、こんな高度な3Dレンダリングはやはり残念ながらできません。
それでもそこまで複雑な3D画像が必要ない場合は簡単な3D画像を作るのにある程度十分でしょう。
追記:映り込みに関しては何とかしました。方法はこの記事で説明しています。
もっと読む
他にもMATLABで3D機能を使ったりアニメーションを作ったりする記事があるので紹介します。
- MATLABでゆるキャラを3D描画
- MATLABでかんたん動画作成
- MATLABとMatplotlib 3dの座標系 | viewの違い > view(azimuth=0) > MATLAB:xaxisが横軸 | Matplotlib:yaxisが横軸 > MatplotlibとMATLABで同じ表示にするには
- [Blender+MATLAB] 有限要素法解析を行い, グラデーションのついた文字を作る!!
- 【MATLAB】3次元形状データ(STLファイル)の扱いについて(読み込み・プロット)
- アホなのでMATLABでレイトレーシングした
- 立体的な🐌かたつむりを描く
- グランディの🌹バラを立体的に描く
- 立体的な🎄モミの木を描く
- 3Dモデルから自動的に生成した画像とアノテーションのデータセットで学習するセマンティックセグメンテーション