・ パスカルのかたつむりが立体に
・ 光源の設置
・ 表面反射の設定
まず2次元の、かたつむり
パスカルの🐌かたつむり については前回の記事をご覧ください
Limaçon of Pascal (Wikipedia English)

MATLABを使って、極座標系で描いたときはこんなふうになります。これは2次元座標の上のかたつむりですが、これを元に3次元のかたつむりをつくっていきます。
さあ、どうやって作ろう?
clear;
t = 0: .001: 2 * pi;
func = @(a,b,t) a * cos(t) + b;
r = func(3, 1, t);
plot(r .* cos(t), r .* sin(t), 'LineWidth', 2);
axis equal;
axis off;
3次元のかたつむり
3次元目を作るのに、Z軸を足す必要があります。Z軸には何か変数をあてがってあげないといけませんが、まずはふつうに θ (上のコード内での変数では t )を Z軸にしてみました。

ところが、くるくる回してみると明らかなように、端が切れてます。つなぎたいです。

図の中の ● は、原点 (0, 0, 0)です。動画がいまひとつカクカクしていて、頼りないのはお許しくださいませ
clear;
close all;
t = 0: 0.1: 2 * pi + 0.1;
func = @(a,b,t) a * cos(t) + b;
r = func(3, 1, t);
f = figure;
f.Color = 'w';
hold on;
plot3(r.*cos(t), r.*sin(t), t, 'LineWidth', 2);
plot3(0, 0, 0, 'o', 'LineWidth', 2, 'Color', [0 0 0], 'MarkerSize', 4);
ax = gca;
ax.View = [64.9016 90.0000];
axis off;
端をつなげる
端と端がつながるように、Z軸を三角関数 sin(t) にしました。ここは、cos関数 でも sin関数 でもどちらでもよく、cos関数だとまたぜんぜん違うものになります
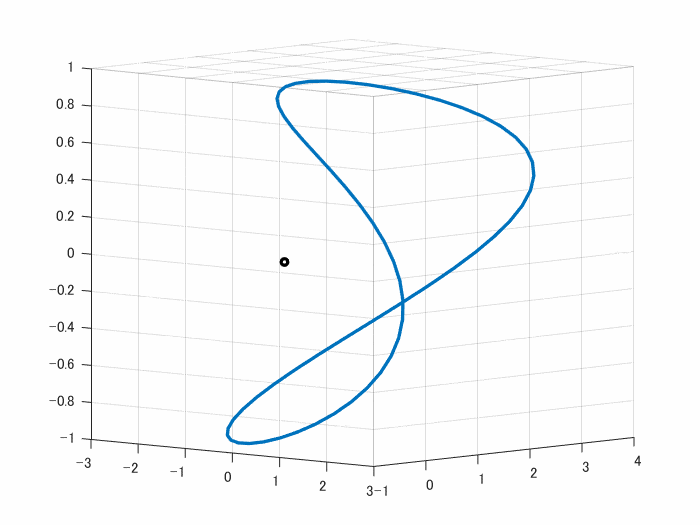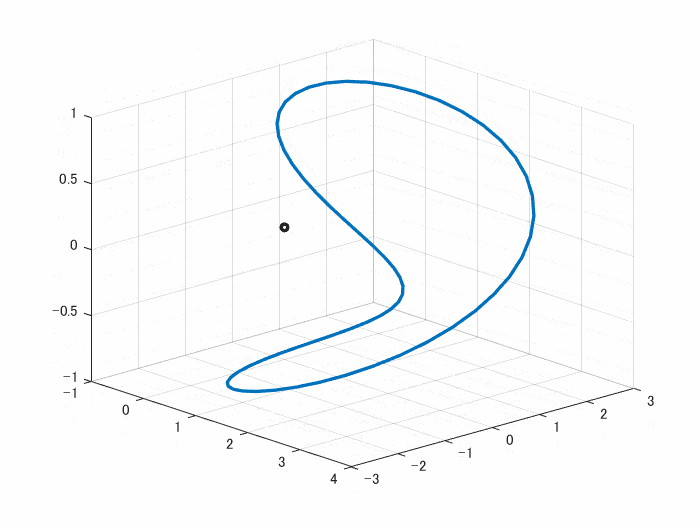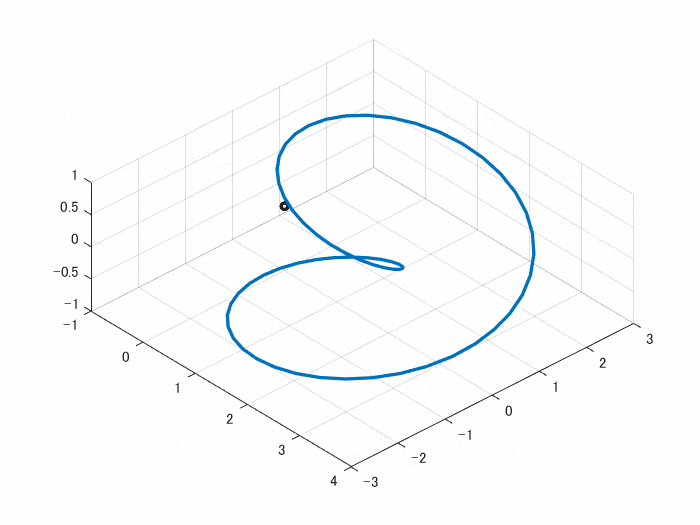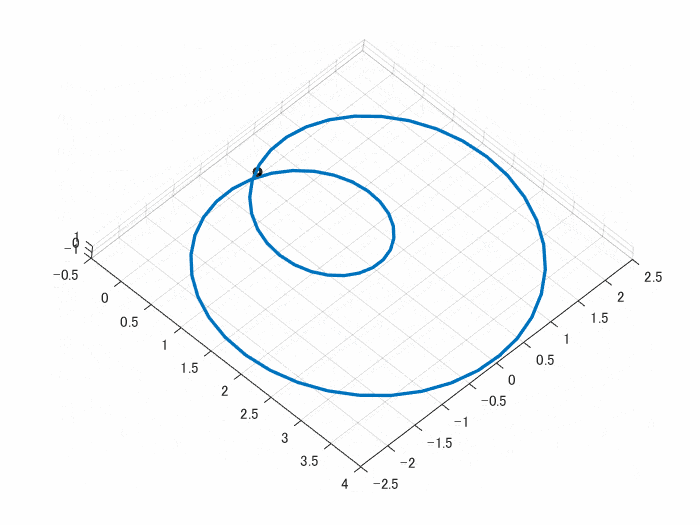
動画にあるように、端が上手くつながっているのがわかると思います
clear;
close all;
t = 0: 0.1: 2 * pi + 0.1;
func = @(a,b,t) a * cos(t) + b;
r = func(3, 1, t);
f = figure;
f.Color = 'w';
hold on;
plot3(r.*cos(t), r.*sin(t), sin(t), 'LineWidth', 2);
plot3(0, 0, 0, 'o', 'LineWidth', 2, 'Color', [0 0 0], 'MarkerSize', 4);
ax = gca;
ax.View = [47.3978 -11.2584];
axis off;
grid on;
竹細工風
もうちょっと工夫をしてみたい気がします。次は parula というカラーマップを使ってちょっと色鮮やかな竹細工風の立体を作ってみました。カラーの指定をしなくても描けますが、デフォルトだと指定色がたくさん出てきてしまうので、parula の、青から黄色の連続したカラーを使ってみました。
ちなみに、parulaは、本来は鳥の名前で、色とりどりのアメリカにいる鳥のことだそうです。直接見たことはないのですが、興味がある方向けには下のWikipediaのサイトに説明があります

上手いこと竹細工のようになりました。原点から線を引いてあり、線の色を parula のグラデーションで変えてあります。
clear;
close all;
t = 0: 0.1: 2 * pi + 0.1;
func = @(a,b,t) a * cos(t) + b;
r = func(3, 1, t);
cm = colormap("parula");
f = figure;
f.Color = 'w';
hold on;
plot3(r.*cos(t), r.*sin(t), sin(t), 'LineWidth', 2);
for k = 1:length(t)
plot3([0, r(k)* cos(t(k))], [0, r(k) * sin(t(k))], [0, sin(t(k))],...
'LineWidth', 2, 'Color', cm(k * 4, :));
end
plot3(0, 0, 0, 'o', 'LineWidth', 2, 'Color', [0 0 0], 'MarkerSize', 4);
ax = gca;
ax.View = [47.3978 -11.2584];
axis off;
ライティング・シェーディング
さて、ここからが本番(?)です。空間の中に照明を設置して、立体かたつむりに照明を当てていきます。かたつむりの殻は、上の竹細工で作った枠に、和紙を張るようにして、三角の patch と呼ばれる面を貼っていきます。
ライティングおよびシェーディングで、光線の加減をつけていきます。図では、わかりやすいように、光源の位置に、丸を付けておきました。

この図形は、もともと上の竹細工と同じもので、本来もっと面が荒いのですが、下のコードの中にある、gouraud という指定をすることで、滑らかな曲面を作ってくれます。
clear;
close all;
t = 0: 0.1: 2 * pi + 0.2;
func = @(a,b,t) a * cos(t) + b;
r = func(3, 1, t);
col = uisetcolor
x = r .* cos(t);
y = r .* sin(t);
z = cos( t);
f = figure;
f.Color = 'w';
hold on;
for k = 1:length(t)-1
p = patch ([0, x(k) , x(k + 1)], [0, y(k), y(k + 1)], [0, z(k), z(k + 1)], col);
p.SpecularStrength = .3;
p.DiffuseStrength = .5;
p.EdgeColor = 'w';
p.EdgeAlpha = .1;
end
Lt = light( "Style","local","Position",[2, -3, 0]);
plot3(Lt.Position(1), Lt.Position(2), Lt.Position(3), 'o');
lighting gouraud;
ax = gca;
ax.View = [110.6585 22.7281];
axis off;
さらに変形
このままだと形が今一つ面白くない感じがして、不満が残ったので、Z軸方向にもう一工夫してみました。そうしたら、こんな編み笠ふうになりました。

clear;
close all;
f = figure;
f.Color = 'w';
hold on;
t = 0: 0.1: 2 * pi + 0.2;
func = @(a,b,t) a * cos(t) + b;
r = func(3, 1, t);
col = uisetcolor
x = r .* cos(t);
y = r .* sin(t);
z = cos(2 * t) * 3;
for k = 1:length(t)-1
p = patch ([0, x(k) , x(k + 1)], [0, y(k), y(k + 1)], [0, z(k), z(k + 1)], col);
p.SpecularStrength = .5;
p.DiffuseStrength = .5;
p.EdgeColor = 'w';
p.EdgeAlpha = .1;
end
Lt = light( "Style","local","Position",[2, -3, -2]);
plot3(Lt.Position(1), Lt.Position(2), Lt.Position(3), 'o');
lighting gouraud;
axis equal;
ax = gca;
ax.View = [68.7268 44.0383];
camzoom(1.8);
axis off;
おわりに
パスカルのかたつむりを変形して作ると、もっといろいろと変な形のものが作れたのですが、とりあえずはここでおしまいにします。ちなみに、こうして作った3次元情報は、.stl ファイルにしてCAD用のソフトに渡すことができます。
自分自身はCAD技術者ではないのですが、過去に3次元モデルを扱ったことがあります。現実の世界にある物と、ソフト内のデータが組み合わさった場面を目にすると、なんとも言えない感じがして、不思議な感覚がわいてきます。