・ 自分で関数(式)を作る
・ 直交座標と極座標
・ 陰関数が便利なときもある
パスカルさん
「人間は考える葦である」で有名な パスカルさん(Blaise Pascal)は、数学や科学一般、哲学で多くの業績を残しました。パスカルさんのお父さんもまたアマチュア科学者であり、熱心に取り組んでいたのが パスカルのかたつむり です
17世紀のことですから、まだこんな便利な時代でなかったので、手で計算して紙に書いていたのでしょう 下のリンクの Wikipediaのページに詳しい説明がありますので(特に英語のほう)よかったらどうぞ
かたつむり
実際に書いてみましょう まずはふつうに極座標を使って書いてみましょう

ちょっとインパクトがある形ですね。かたつむりの式は、直交座標系ですとこんな感じです
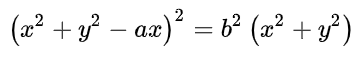
a の値や、b の値を変えると、小さい丸部分と、大きな丸部分の比率が変わり、形態自体がかわります どの値がいいんだろ? って、a や b を変えてしばらく試していました
clear;
t = 0: .001: 2 * pi;
r = 2 * cos(t) + 1;
plot(r .* cos(t), r .* sin(t));
axis equal;
axis off;
MATLABで極座標を使って簡単に書くとこんな風になります 上の直交座標の式を、極座標を使って表したものです。原点を中心にくるくる回しながらプロットするので、中心の角度 θ (theta) を、 0 ~ 2 × π までの 0.001(単位はラジアン)刻みの行列 t として作成します
無名関数を使って描く
さて、次に、同じものを少し違う形で描いてみましょうね 下は a = 3 , b = 1 の場合の形です 真ん中が少し大きくなった!

コードのほうはちょっと趣を変えて、無名関数を使ってみました
clear;
t = 0: .001: 2 * pi;
func = @(a, b, t) a * cos(t) + b;
r = func(3, 1, t);
plot(r .* cos(t), r .* sin(t), 'LineWidth', 2);
axis equal;
axis off;
増やしてみる
次に、θ の部分に、掛け算や割り算を加えて、ちょっと複雑な形にしてみました
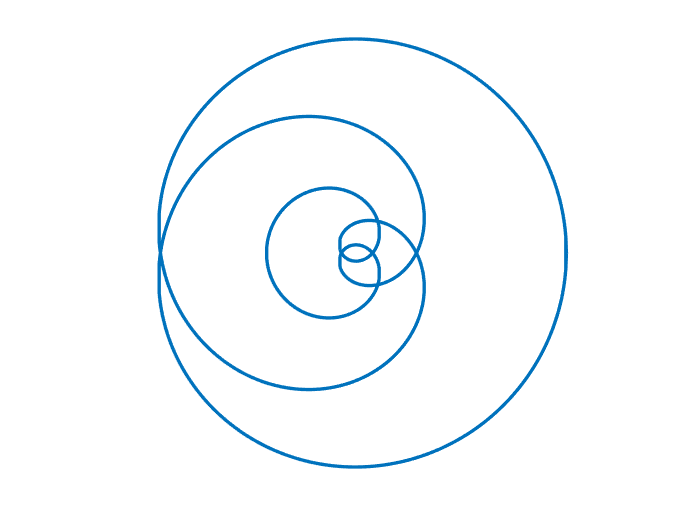
clear;
t = 0:.001:12 * pi;
func = @(a, b, t) a * cos(t) + b;
r = func(2, 1, t);
plot(r .* cos(t * 4), r .* sin(t *4), 'LineWidth', 2);
axis equal;
axis off;
重ねてみる
次のバリエーションは、ちょっとべたな感じではありますが、角度を 90 ° ずらしながら、重ねていきましょう
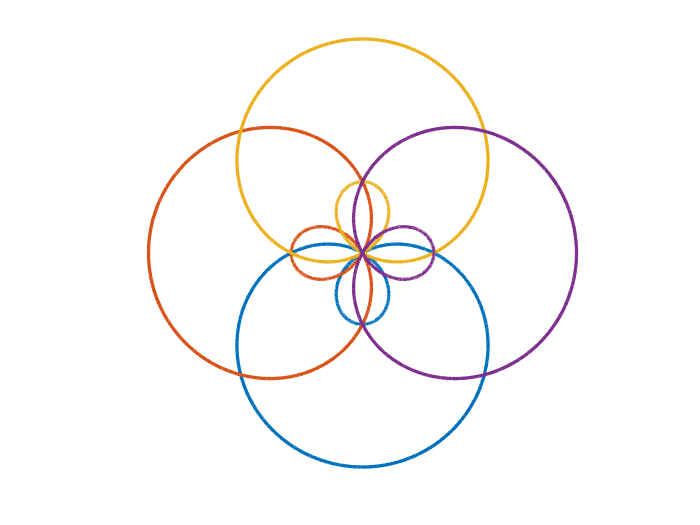
clear;
t = 0:.001:2* pi;
func = @(a, b, t) a * cos(t) + b;
r = func(2, 1, t);
figure;
hold on;
plot(r .* cos(t + pi * (-.5)), r .* sin(t + pi * (-.5)), 'LineWidth', 2);
plot(r .* cos(t + pi), r .* sin(t + pi), 'LineWidth', 2);
plot(r .* cos(t + pi * .5), r .* sin(t + pi * .5), 'LineWidth', 2);
plot(r .* cos(t + 2 * pi), r .* sin(t + 2*pi), 'LineWidth', 2);
axis equal;
axis off;
パスカルのかたつむりは、子供のころから本で読んで知っていた形ですが、描いてみたのは今回がはじめてです
かたつむりに似てないじゃん、という意見もあるかもしれませんが、まあまあいいの。a の値や、b の値を変えることで3個の形態を持つのが魅力的です。パスカルのお父さんは、たぶん仕事のあとの楽しみとして、コツコツと計算して、それを明らかにしようとしていたのでしょう
陰関数によるプロット
陰関数というのは、式の値が 0 になる関数です。
f = x + y
であれば、無名関数で書くと、こういうことを意味します
f(x, y) = @(x, y) x + y
f(x, y) = 0
陰関数 (implicit function) は、f(x, y) の値がゼロになることを前提とした表し方です fimplicit を使うと、陰関数として f(x, y) を、直接 x と y の直交座標ベースでプロットしてくれます

かたつむりを、陰関数を使って 書くとこんな風になります
clear;
func = @(x, y) (x^2 + y^2 - 2 * x)^2 - (x^2 + y^2);
h = fimplicit(func, [-.5, 3.5, -2, 2]);
h.LineWidth = 2;
axis equal;
axis off;
陰関数を使うと、x, yの式だけが与えられたときに、θ に置き換えて極座標系にする手間がいらなくなります [-.5, 3.5, -2, 2]は、座標軸の範囲に関する数値で、X軸とY軸の範囲をそれぞれ最大値、最小値の順で示したもので、なくてもデフォルト設定があるので描けます
便利ですね
補足
MATLABは便利ですが、ヘルプの文書がわかりにくいことがあります。 一次元の行列のことを、ベクトルと呼びます。 また、上の例で、行列どうしの掛け算の場合 .* や ./ .^を使っています。 たとえば、.* の場合ですと、行列の要素をそれぞれの端から順番に掛けてくれて、別の行列を作ってくれます。 スカラーというのは、ひとつの数値のこと(数字で表現した大きさ)を意味します
お知らせ
この記事は、同じQiita内の立体の🐌かたつむりへ続きます。よかったらお越しください。2023年12/17以降閲覧可能になります。