ことの発端
急に思いついてしまったのです。なんか、こう、降ってきたっていうか?意外とそういうタイプなんすよね私。
誰の役に立つのかさっぱりわからない記事です。ご了承ください。
まずレイトレーシングとは何か
MATLAB原理主義者やSimulink過激派の皆さんはレイトレーシングというもの自体に馴染みがない方が多いと思いますので、そこから一度説明しておきます。
レイトレーシングとは、光線(レイ)が反射・透過していく過程を追跡し、(ある程度)物理に忠実な光の伝搬を計算する解析手法です。解析手法というと厳かですが、映画やゲームのCG作成に使用されるなど、近年では一般人の目に触れる機会が増えてきています。
下図1はグランツーリスモ7のデモ画像で、車が床面に反射していたり、天井のライトの影が正確に落ちていたり、そのあたりの計算にレイトレーシングが活用されています。
ある程度物理に忠実と言っているのは、電磁気ガチ勢の人からすると結構近似的に見えるためです。
計算の流れはさまざまな手法がありますが、中でもシンプルなものを簡単に紹介します。
レイの照射
まず、物体とカメラを用意します。
レイの解析によって、カメラセンサの各ピクセルにどういう光が帰ってくるかを計算します。
光を追跡するという原理から言えば、光源からレイを発射するのが筋ですが、効率が悪いので逆にカメラからレイを発射します。
レイの衝突
レイは数学的いえばベクトルです。カメラから出てきたベクトルがどの位置に衝突するかを計算します。そののち、その物体に設定した材料情報から、カメラに返ってくる光の色を計算してピクセルに加算します。
影判定
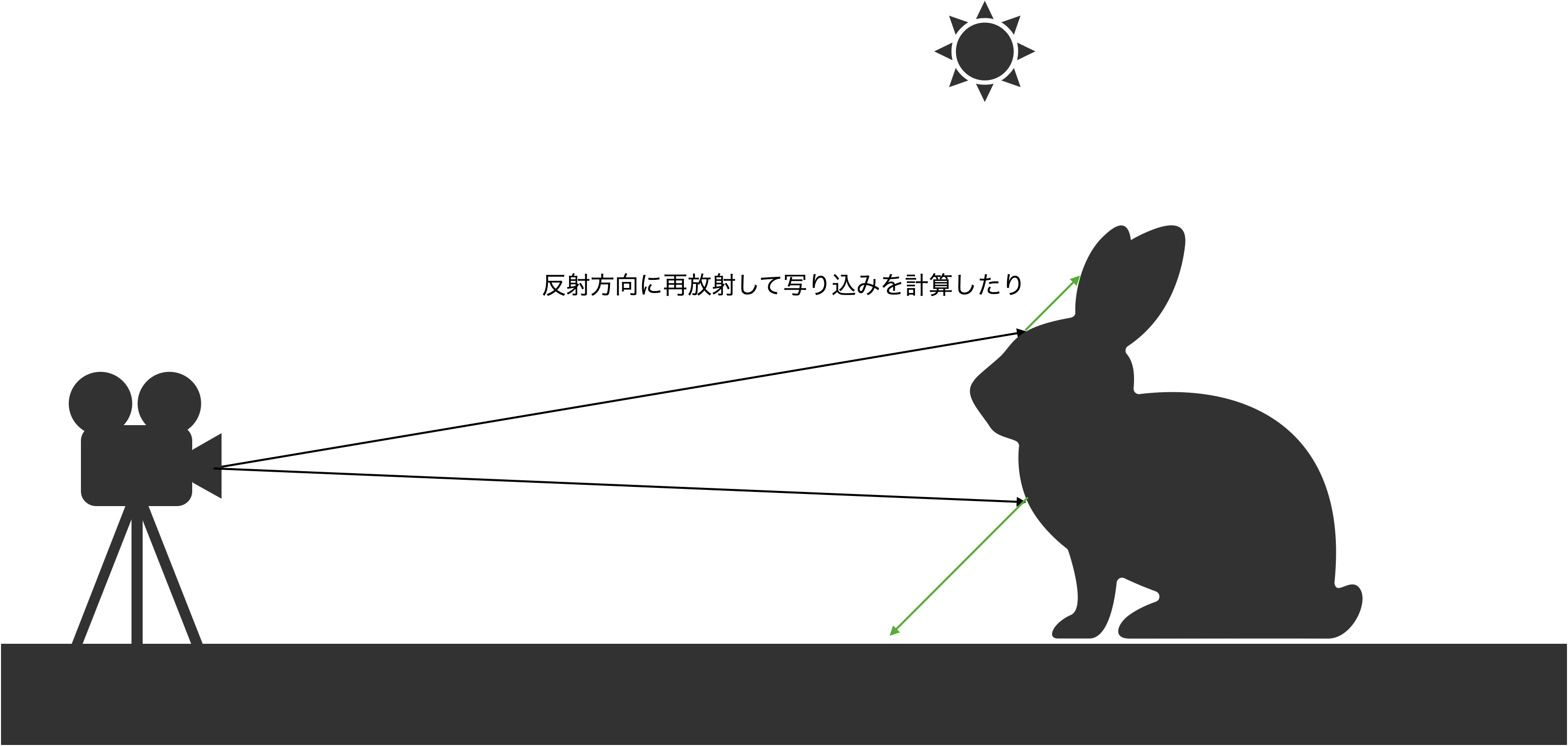
カメラに変える光を計算する際、衝突地点から光源に向かってレイを再放射することで影になっているかどうかを判定し、ピクセルに返す色に反映することができます。
写り込み
また、衝突地点から反射方向にレイを再放射・衝突判定をして、写り込みの色をピクセルに足し込むことができます。
そのほか
そのほか、透過・屈折・散乱など、再現したいものに応じてさまざまな計算手法を取ります。
構成要素
レイトレーシングをするうえで必要な要素の説明です。
設置物のモデル
描画対象の3Dモデルのデータ構成を説明します。よりリアルで正確な描画を求めるなら工夫の余地がありますが、今回は基本的なものに絞って作ります。
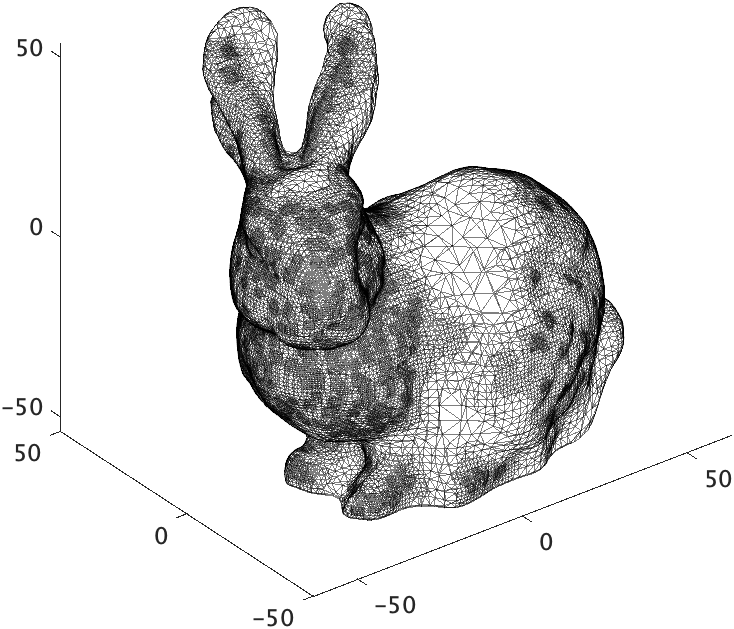
三角形ポリゴン
立体のものを保持する手法の基本的なものは三角形ポリゴンです。立体形状を細かい三角形の張り合わせで近似するやり方で、曲面などは厳密に再現できませんが、見た目上ほとんど問題のない品質にはできます。
これは頂点と頂点インデックスによって構成されていて、MATLABのpatch関数の引数VerticesとFacesに対応します。詳しいことはここでは省略しますが、頂点というのは形状を構成する点群座標をそのまま配列化したもので、頂点インデックスは、何番目の頂点をつなげて三角形を構成するかを配列にしたインデックス配列です。
法線
今回は頂点放線を使いますが、理解が簡単な面法線も説明しておきます。
面法線
面法線は、各三角形に垂直なベクトルで、ある面がどちらを向いているか、どちら側が表面かを示すベクトルです。
頂点法線
頂点法線は、各頂点に割り振られた法線方向ベクトルで、その頂点における垂直方向を示します。面法線と同じ向きである保証はありません。
三角形ポリゴンは厳密な曲面を再現できないので、この頂点法線によって曲面っぽい陰影をつけることでごまかします。
衝突判定
レイトレーシングでは、レイと設置物との衝突判定をする必要があります。今回は三角形ポリゴンに絞っているので、三角形とレイとの衝突判定を説明します。
レイは始点と方向を持つベクトルで、それと三角形を含む平面との交点を求め、その位置が三角形内である時に衝突したと判定します。
高校数学のベクトルの範囲内で解けますが、一般的にはその最適化手法であるTomas Mollerの交差判定法を使います。詳しくは以下のページを参照してください。
空間構造
レイトレーシングで最もコストがかかるのが、全三角形とレイの交差判定をして、最も近距離で衝突した三角形を抽出する作業です。愚直に計算すると、$N$個の三角形ポリゴンの物体を設置した場合、反射回数が1回(映り込みの計算をしない)の場合でも、$O(N)$、最大の反射回数が$K$回の場合だとおおよそ$O(NK)$の計算量になります。
レイを飛ばして交差判定をする一連の作業をトレースというのですが、トレースの作業を軽くするために、空間構造という空間の最適化を行います。
今回はメジャーなBVHを説明します。
BVH (Bounding Volume Hierarchy)
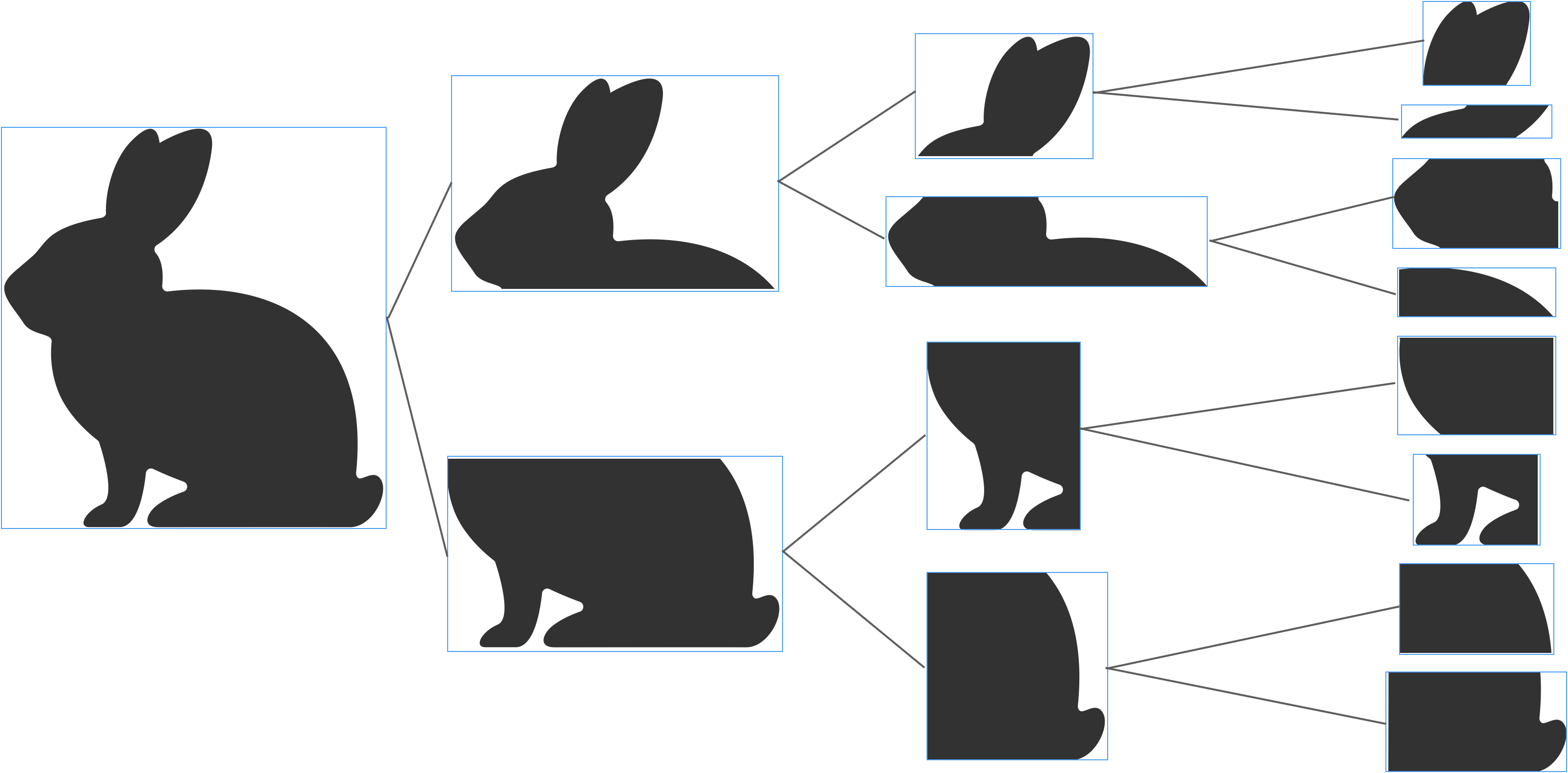
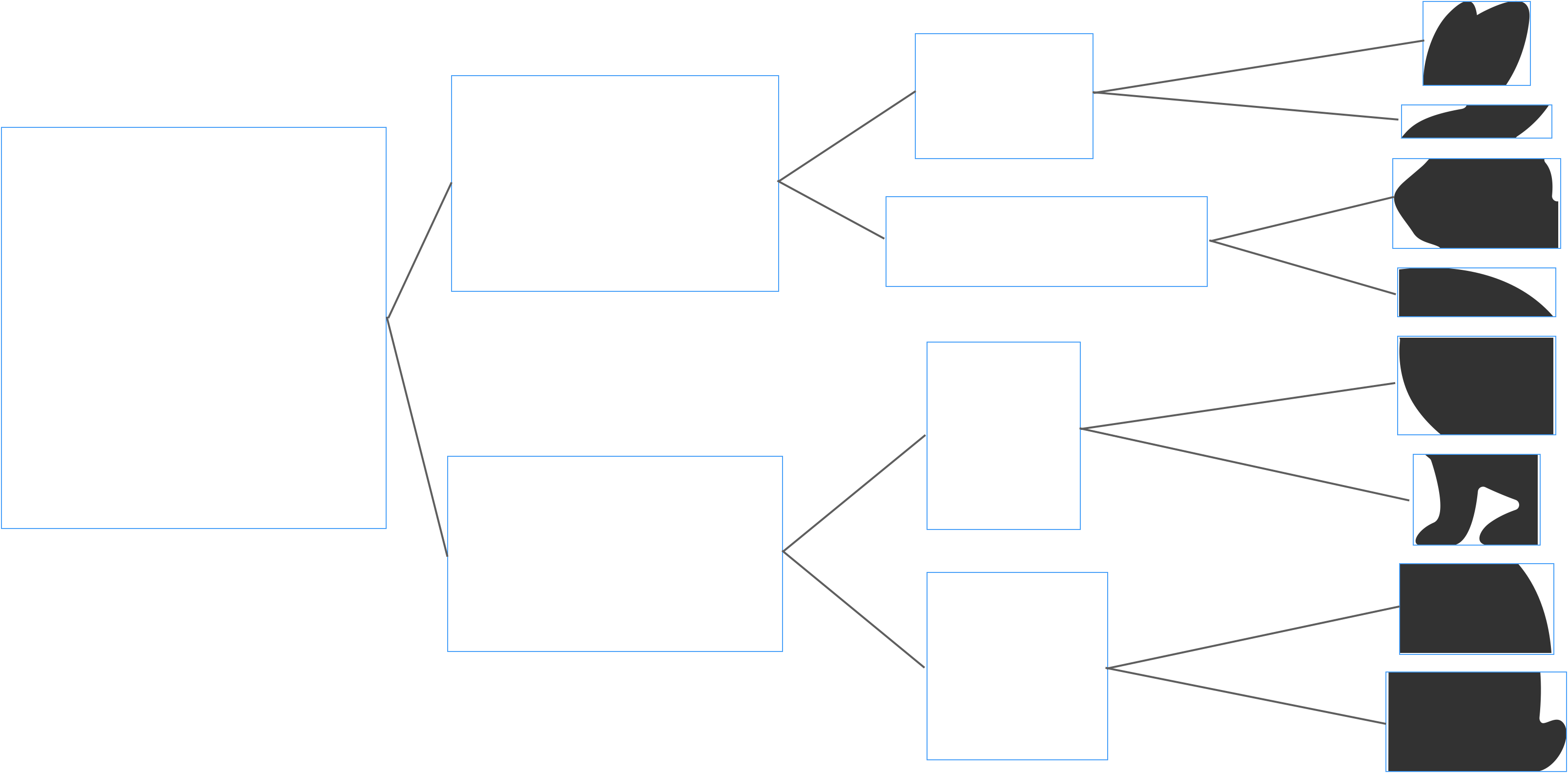
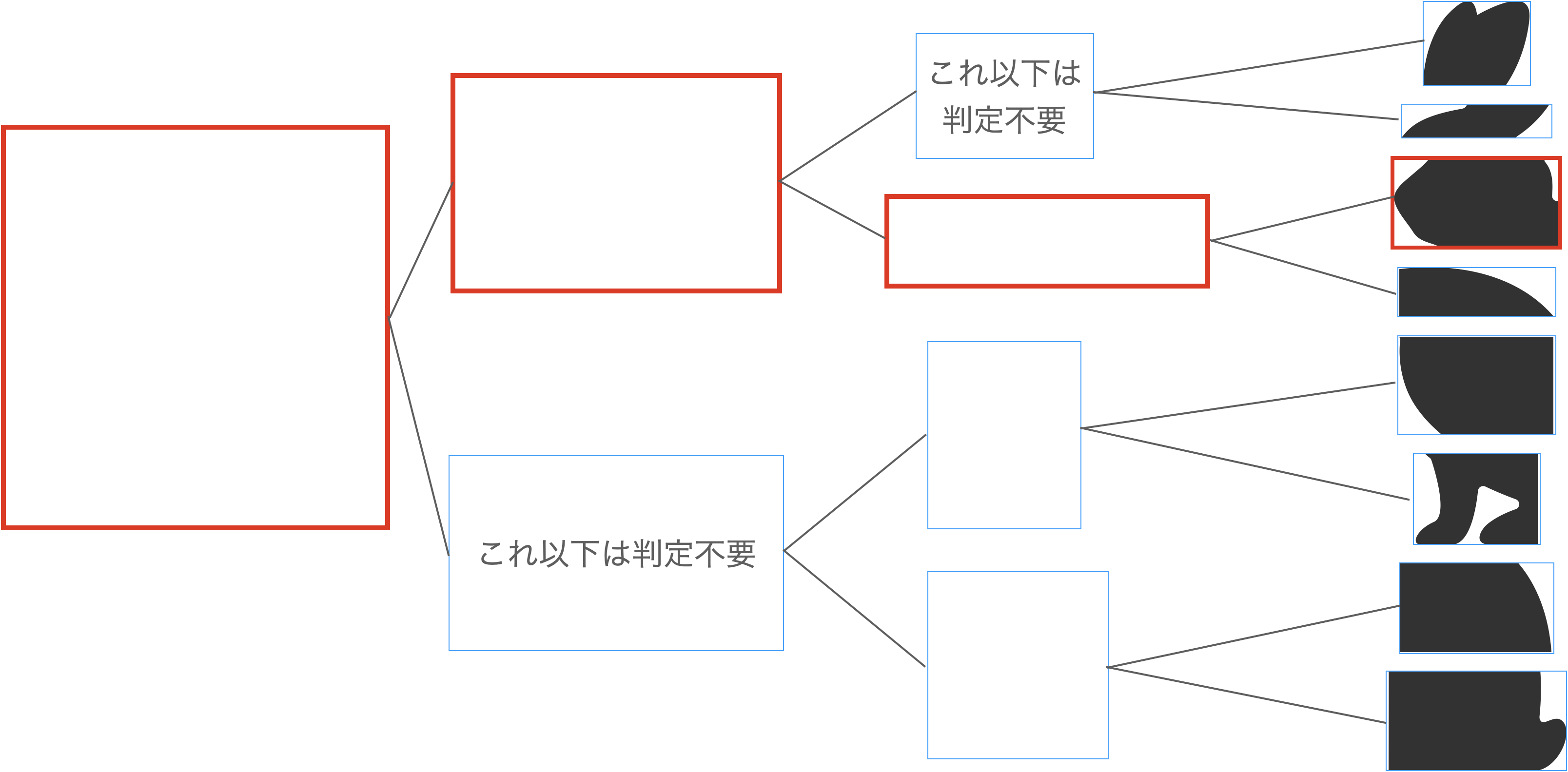
BVHはポリゴンをその位置によって木構造で管理する構造で、ポリゴン全体を囲むバウンディングボックスを2つに区切って枝として、その枝をまた2つに区切って枝として、、、を繰り返し、枝に含むまれるポリゴン数が適当なサイズになるまで繰り返します。
バウンディングボックスとは、ある形状を過不足なく囲う直方体のことです。
上の例では、ウサギのポリゴンをいい感じのところで2分割し、分割されたものをまた分割し、を繰り返して細かいポリゴン群に分けています。ここで重要なのは、中間の枝のバウンディングボックスは、それ以下の枝に繋がるポリゴンを空間的に全て包含しているということです。
上の絵では、中間の枝にもポリゴンが保存されているように見えますが、実際にはポリゴンは終端の枝にのみ格納され、中間の枝にはバウンディングボックスのみがある状態です。
今回はMATLABでやっているので、ある程度の三角形数であればノードの行き来よりも、行列での一括計算の方が高速になるので、最終ノードの三角形はそこそこ残してあります。c++などでやるなら三角形数個レベルまで分岐した方がいいかもしれません。
BVHを用いた衝突判定の高速化
BVHを構築することで1回の衝突判定あたりの計算量を格段に減らすことができます。レイの衝突判定をする際は、以下のような流れで計算すると、計算量を格段に削減できます。
- 一番親のバウンディングボックスと、レイが交差するかを判定する。
- 交差しない時は、どのポリゴンとも衝突しない。
- 交差する場合は、子ノードのバウンディングボックスとレイが交差するか判定する。
- 交差しなければそのノード以下のポリゴンとは衝突しない。
- 交差する場合は孫ノードのバウンディングボックスとレイが交差するか判定する。
- 以降繰り返し。最終ノードになったらそのノードないのポリゴンと衝突判定する。
BVHのバウンディングボックスは、子ノードのボックスを包含しているので、どこかのバウンディングボックスと非衝突だった場合、その子ノードに入っているポリゴンとは衝突しないので判定する必要がありません。
これによって衝突判定のコストを対数的な増加に抑えることができます。
シェーダ
シェーダとはレイが物体にぶつかったときにどういう色を出力するかを決定するモデルです。
今回はPBR (Physically Based Rendering)に挑戦してみました。
PBRと従来のシェーダの特徴
上図2のように、古典的なシェーダは物質のベース色、光沢の鋭さ、影部分の色合いなど、見た目を直接操作するパラメータを与えていました。処理は簡単なので、計算リソースが貧困な場合はこちらが主流です。
一方でPBRは、ベースの色、ラフネス、金属かどうかなど、材質を操作するパラメータを与え、それを元に色計算モデルを介して、出力色を決定するものです。そのために出てくる色が現実に近く、エネルギー保存もある程度は正確なので、レイトレースなど写り込みを計算する際に、違和感のある光沢感になったりしにくいのが特徴です。
PBRの仕組み
PBRの前にレンダリング方程式を紹介しますが、あまり数式を出しすぎても混乱するので、言葉で説明します。
まず、物体に光が入射し、視点方向に返ってくる場合、以下のような基本式で計算します。
$$\text{カメラに帰る色}=\text{発光}+\sum(\text{反射分布関数}\times \text{入射の色}\times \text{入射角度の余弦})$$
発光は今回考えないものとします。
重要なのは反射分布関数で、ここが材質から色を決定する部分です。反射分布関数はさらに以下のように表せます。
$$\text{反射分布関数}=\text{拡散成分} + \text{光沢成分}$$
拡散成分をdiffuse、光沢成分をspecularと呼んだりします。もっと正確に言えば透過とかもあります。
レイが衝突するたびにこれを計算していくわけです。
Unreal Engine 4の反射モデル
今回はUnreal Engine 4に搭載されているPBRをちょっと真似て実装しました。拡散成分は
$$\text{Diffuse} = \text{base color}/\pi$$
光沢成分は
$$\text{Specular}=\frac{FDG}{4\cos{\theta_i}\cos{\theta_v}}$$
となります。$F,D,G$は、それぞれフレネル項・法線分布関数・幾何減衰です。
拡散成分
拡散成分は、光が入射角にほぼ関係なく一様に分散する様を表現する項です。平たくいうと物質の色ですね。
Unreal Engine 4ではLambert反射モデルが使われていますが、Oren-Nayarモデルなど、より物理に正しいモデルもあります。UE4はゲームエンジンなので計算を軽くするために、多少物理に反しますがLambertを採用したみたいです。
光沢成分
フレネル項
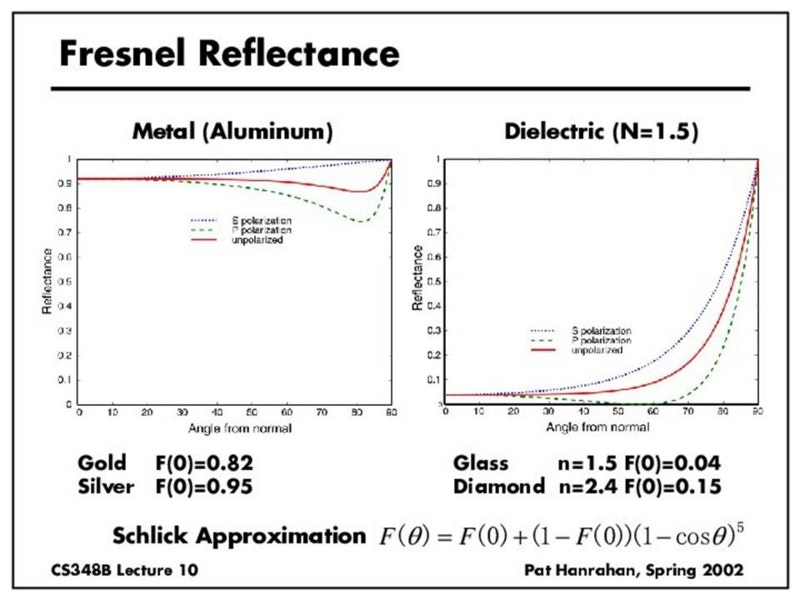
電磁波が物体表面にある入射角をもって入射する時、その入射角によって反射率が変わる現象をフレネル反射といいます。厳密には入射角の他に偏波も反射率に影響するのですが、CGで使うフレネル項は、Fresnel-Schlickによる近似式が多く、この近似では偏波の影響が無視されて、水平垂直偏波の中間をいくような反射率変化をします。3
これを見ると、垂直入射の時に反射が最も少なく、水平入射に近づくほど全反射に近くなっています。
そして、非金属(=誘電体)は垂直・水平入射間の反射率の差が大きく、金属だと小さいことがわかります。(理論的には金属は入射格依存がないのが正解のはずですが、実際は表面状態や酸化被膜などで多少変化するようです。)
法線分布関数
法線分布関数と幾何減衰項は、ともに表面のラフネスによる光沢変化を近似するものです。
物体表面には、光の波長のスケールでしかわからないほどの凸凹(マイクロファセット)があり、これによって反射光は多少散乱します。
法線分布関数はその名の通り、どの程度の面積が反射方向に反射光を飛ばすかを表します。
幾何減衰項
マイクロファセットはスケールは小さいですが凸凹です。したがって、ある位置の面がいくら反射方向に反射光を返すと言っても、少しずれた位置の面で遮蔽されるかもしれません。
この遮蔽の確率をモデル化したのが幾何減衰項です。
法線分布関数と幾何減衰項はニコイチなもので、法線分布にあるモデルを使用したら、それにマッチする幾何減衰項モデルを使わないといけません。有名なものではGGXがあり、今回はそれを使います。
金属パラメータ
拡散成分と光沢成分を1対1で足すと、金属っぽさの表現ができません。この辺は詳しくないのもあってサッと通り過ぎてしまいますが、金属であるほど拡散成分は小さく、非金属であるほど大きくなります。その代わりに、金属であるほど光沢成分に素地の色がのり、非金属であるほど光沢は白っぽくなります。
ですので、最終的な反射分布関数はこんな感じになります。
$$\text{反射分布関数}=\text{金属っぽさ}\times\text{拡散成分} + (1-\text{金属っぽさ})\times\text{光沢成分}$$
金属っぽさパラメータは、ほとんど0か1ですが、先にも少し説明した通り、金属でも1ジャストということはあまりなく、酸化被膜やコーティングなどの影響で0.9・・・とかにするといいようです。
出来栄え
出来上がったものがこちらです。
なかなかリアルな画像ができたのではないでしょうか。
この1920x1080の画像のレンダリングにかかった時間はなんと200s!!!
遅い!!!
(この程度ならGPUでやれば一瞬で終わります。)
ちなみに物理ベースシェーダなので、簡単に金属っぽくできます。
似たようなことをする人へアドバイス
フルスクラッチでのレイトレをMATLABでやる人はほぼいないと思いますが、一応アドバイスというか感じたことを書いておきます。
メモリに注意
MATLABは基本的に実体渡しをするものです。関数を作っても参照にはできません。(そのはず。違ってたらすいません。)
今回は多くの頂点情報を参照したい部分がたくさんあるので、できるだけ渡す情報を減らすとか、メモリに余裕のあるPCにするとかしましょう。
クラスをうまく使おう
ジオメトリ・レイ・ヒット情報・BVHなど、全てグローバル変数で管理してたら煩雑でやってられません。
メンバ関数とかしっかりしたこと考えなくてもいいので、とりあえずレイヤーごとに変数をクラスにした方がいいです。
まとめ
久しぶりに馬鹿げたことをやってみましたが、フルスクラッチすると意外と理解できていなかった点とかが浮き彫りになって勉強になりますね。
レイトレーシングはいろんなライブラリがあるので、C++とかを使う人は意識しないかもしれないですが、BVHなど計算の工夫が随所に感じられて、より深く理解できた気がします。