はじめに
・キッチンスケールで小麦粉の重さを量る
・Bluetoothイヤホンで音楽を聴く
・GPSで今いる場所を確認する
これら全ての基礎になる技術が信号処理です。
そして信号処理で扱うあらゆる信号には影のようにつきまとってくるものがあります。
そう、ノイズですね。
・電源ラインから入り込んでくるノイズ
・モータの振動によるノイズ
・電子回路のクロストークノイズ
原因は様々ですが通常、信号とノイズは必ずセットで扱わなければなりません。
最も有効なノイズ対策はノイズ源そのものを除去することですが、例えば工場での重量計測において、計測中は周囲で動いてる装置を全部止めて振動を無くしましょう!なんて現実的ではありません。
そこで活躍するのがフィルタ技術、とりわけデジタル(ディジタル)フィルタです。
このシリーズではフィルタ設計法習得に向け、フィルタ設計と信号処理の基礎に関する直感的な理解を目標に解説していきたいと思います。
なるべく数式を排して取っつきやすい説明を行っていくつもりなので、やや不自然な言い回しや誤解を招きかねない表現があるかもしれません。
そういった箇所を見つけられた場合はすみませんが、ご指摘頂けると幸いです。
本記事はその STEP4:ノイズ除去実践編 です。
他STEPへのリンクは下記です↓
STEP:0 導入編
STEP:1 フィルタ特性の見方
STEP:2 インパルス応答とフィルタ
STEP:3 周波数領域における伝達関数
簡単なフィルタ設計&性能評価をやってみたい方は下記もどうぞ↓
FIRローパスフィルタを作ってみよう!
1. 前回のおさらい
前回は周波数領域での伝達関数の表現方法と、周波数領域で表現した伝達関数からフィルタの振幅特性及び位相特性を求める方法について説明しました。
加えて、フィルタの遅延時間に関して群遅延とステップ応答時間という2種類の時間的な遅れを示し、伝達関数を用いてそれぞれ定量化しました。
前回のおさらいを下記に簡単にまとめます。
<周波数領域での伝達関数>
離散信号すなわちデジタルな信号を扱う際に用いられるz変換 を元に$z$を使用して表現された伝達関数において、z変換と離散時間フーリエ変換の定義から $z$は$z=e^{jω}$と置き換えることができます。 このとき$ω$は角周波数、$j$は虚数単位です。
したがって、$z$を使った伝達関数に$z=e^{jω}$を代入すれば周波数を含んだ形で伝達関数を記述することができます。
下記にFIRフィルタとIIRフィルタの伝達関数を周波数を含んだ形で書き表します。
・FIRフィルタ
$$
H(e^{jω}) = \sum_{n=0}^{N} b_n e^{-jωn}
$$
・IIRフィルタ
$$
H(e^{jω}) = \frac{(\sum_{n=0}^{N} b_n e^{-jωn})}{(1 + \sum_{n=1}^{M} a_n e^{-jωn})}
$$
ちなみに角周波数$ω$(単位はrad/secです)と周波数$f$(Hz)の間は$ω=2πf$の関係なので、$e^{jω}=e^{j2πf}$と書くこともできます。
周波数領域でフィルタの伝達関数を表現することにより、フィルタの振る舞いも周波数軸上で解析することができます!
<伝達関数によるフィルタの解析>
伝達関数を$H(e^{jω})$としたとき、フィルタの振幅特性と位相特性は下記の通りです。
$$
振幅特性 : |H(e^{jω})|
$$
$$位相特性:\angle H(e^{jω})
$$
この式から、振幅特性は伝達関数の絶対値、位相特性は伝達関数の偏角であるということが分かります。
※ちなみに、もちろんこれはFIRフィルタ/IIRフィルタ関係無く同じ式になります。
実際には手計算で伝達関数から絶対値や偏角を求めるのは面倒なので、通常はPythonやMATLAB等のツールを使用してコンピュータに計算してもらえば良いと思います。
<フィルタの時間的遅れ>
・群遅延
フィルタを通ることによる、信号の時間的な遅れのひとつ目は群遅延です。
群遅延はフィルタの位相特性を周波数ごとに微分したもので、定義式は次の通りです。
$$
群遅延 = -\frac{d}{dω}\angle H(e^{jω})
$$
周波数ごとの微分なので、言い換えると各周波数成分に対する位相変化の傾きを示します。
直感的な意味としてはフィルタを通ることによる時間的な遅れを周波数成分ごとにプロットしたものと言えます。
FIRフィルタ/IIRフィルタの位相特性と群遅延を下記に示します。
・FIRフィルタの位相特性と群遅延
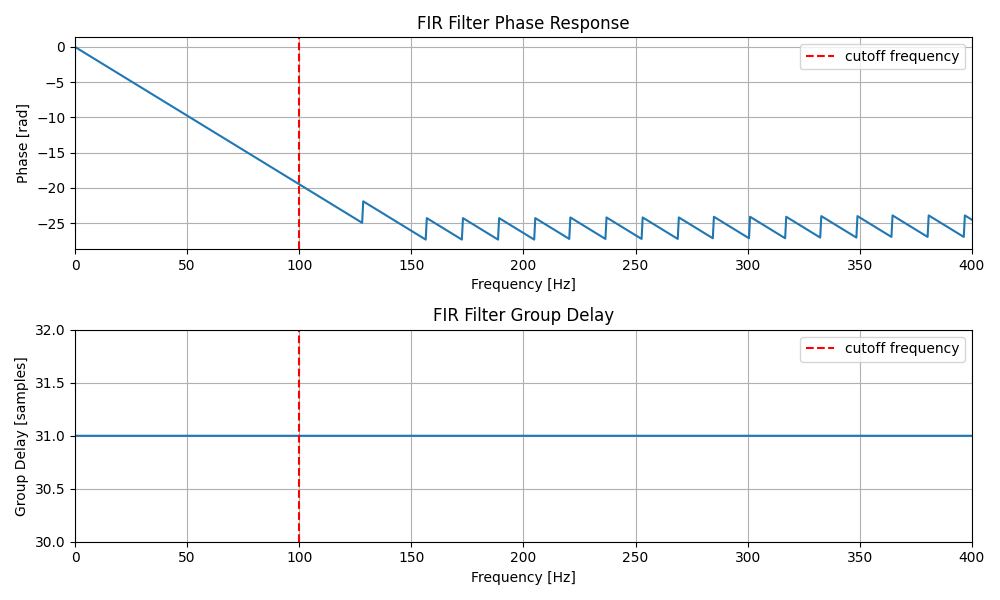
・IIRフィルタの位相特性と群遅延
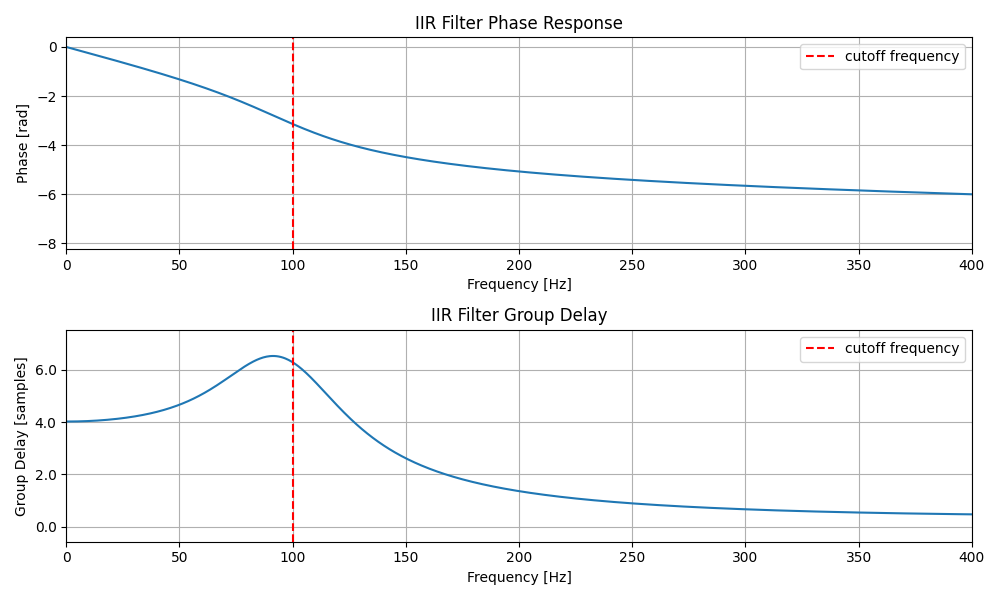
FIRフィルタの群遅延はまっすぐな線になっていますが、これはこのFIRフィルタは線形位相特性を持っており、位相変化の傾きは一定、すなわち群遅延も一定になるためです。
一方で、非線形位相特性を持つフィルタであれば、位相変化の傾きに応じて群遅延が変化します。よって、上記IIRフィルタの図では群遅延も周波数ごとに変化しています。
・ステップ応答時間
例えば重量計測のようにフィルタを通して得たい信号が定常的な値である場合、群遅延よりもステップ応答時間を用いて時間的な遅れを表した方が好都合な場合があります。
下記にFIRフィルタとIIRフィルタにステップ入力を与えた場合の出力を図示します。
※ステップ入力は0時刻目から立ち上がって以降、ずっと1が続くような信号です。
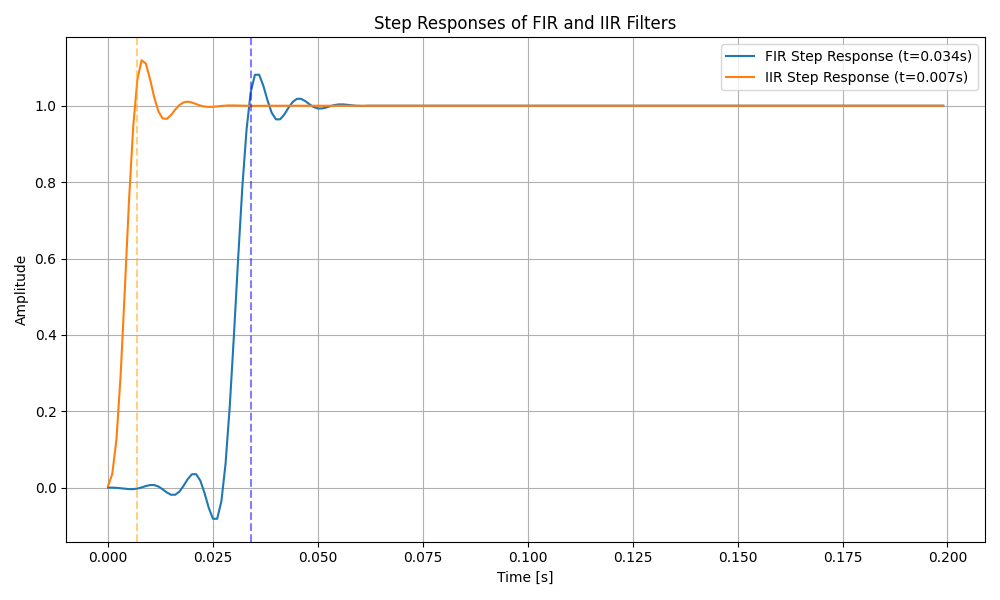
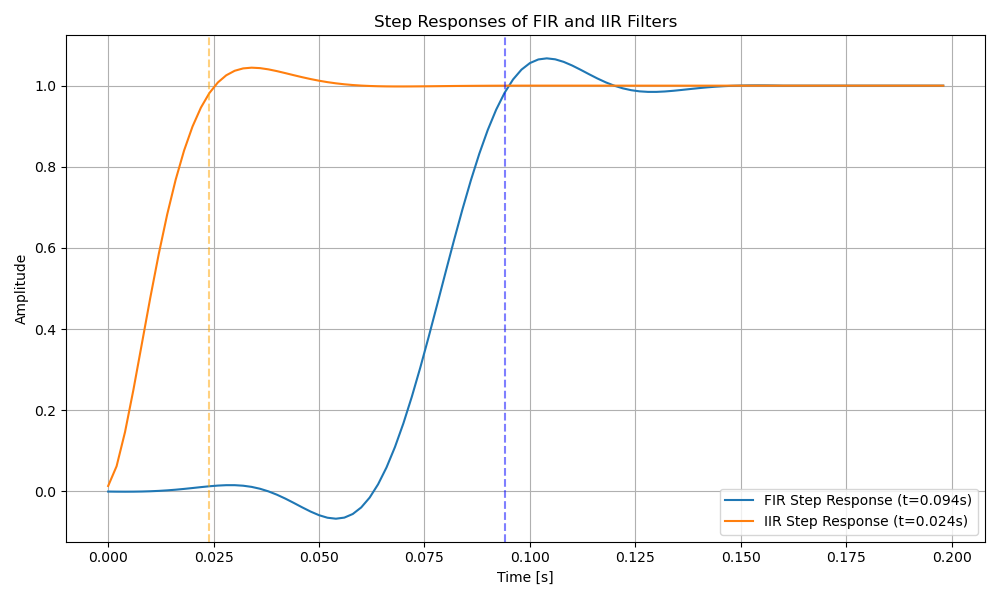
・FIRフィルタとIIRフィルタのステップ応答
この場合はFIRフィルタが0.034(sec)、IIRフィルタが0.007(sec)とIIRフィルタの方が早く出力が収束しています。
ステップ応答時間の求め方はFIRフィルタとIIRフィルタでちょっと違います。
・FIRフィルタのステップ応答時間
FIRフィルタの伝達関数は以下です。
$$
H(e^{jω}) = \sum_{n=0}^{N} b_n e^{-jωn}
$$
このFIRフィルタの伝達関数は「出力がn=0からNまでのインパルス応答の累積和で構成されている」、言い換えると「累積和が取れるまでちゃんとした出力が出てこない」ということを意味します。
通常「n=0からNまで」のnの個数、すなわち「N+1」のことをフィルタ次数とかタップ数、フィルタ長と呼び、フィルタ次数によって累積和が取れるまでの時間は変化します。
そしてステップ応答時間は累積和が取れるまでの時間と考えて良いので、結局、秒としてのFIRフィルタの最大ステップ応答時間は下記によって求められます。
$$
FIRフィルタのステップ応答時間 ≈ フィルタ次数×サンプリング周期
$$
※厳密には完全に一致はしませんが、実用上は上記の式で考えて良いです。
※設計によって、実質的にはもっと速く収束することもあり得ます。
・IIRフィルタのステップ応答時間
IIRフィルタの伝達関数は以下です。
$$
H(e^{jω}) = \frac{(\sum_{n=0}^{N} b_n e^{-jωn})}{(1 + \sum_{n=1}^{M} a_n e^{-jωn})}
$$
IIRフィルタの場合は出力のフィードバックがあるため、インパルス応答が(理論上)無限に継続し、収束しないのでした。
そのため、FIRフィルタと同じようにフィルタ次数のみでステップ応答時間を求めることはできませんが、収束しないというのはあくまで理論上の話であって実際のインパルス応答は指数関数的に減衰していきます。
よって、IIRフィルタの場合は「ステップ入力を受けて、出力が99%に達するまで」等の閾値を設けて、近似的にステップ応答時間を求めます。
近似する方法として理論的に近似することもできますが、実用上は実際に信号をIIRフィルタに通して実測するのが手っ取り早いです。
よって、IIRフィルタのステップ応答時間は下記のようになります。
$$
IIRフィルタのステップ応答時間 ≈ インパルス応答の収束時間(定義や近似方法は様々)
$$
前回までのお話で、フィルタの入出力関係の周波数領域での解析と、それを時間軸に移して性能比較/評価を行う準備が整ったので、今回は実践編として信号のノイズ解析・フィルタ設計・結果確認までのシミュレーションをしてみましょう。
2. 信号のノイズ解析
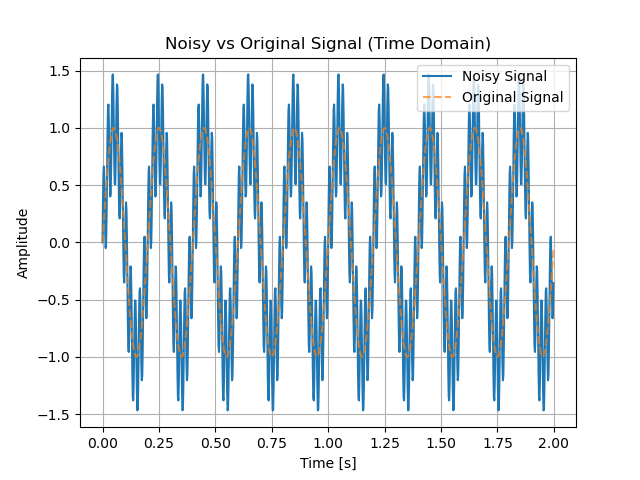
シミュレーション用に、下記仕様の信号を作ります。正弦波の元信号にノイズを重畳させたものですね。
元信号と元信号+ノイズ信号を併せて表示しています。
・元信号:5Hzの正弦波
・ノイズ:50Hz
・サンプリング周波数:500Hz
さて、今回はシミュレーションなので、元信号・ノイズ・サンプリング周波数の全てが分かっています。ただ、実際に現場でノイズ除去を行う場合、ノイズの周波数が不明な状態から作業を始めることがほとんどです。
つまり、下記の状態ですね。
・元信号:5Hzの正弦波
・ノイズ:?
・サンプリング周波数:500Hz
むしろ場合によっては、こうなっていることもあります。
・元信号:?
・ノイズ:?
・サンプリング周波数:?
この場合は元信号、サンプリング周波数に関してはどんな機器を使用して、どんな信号を取得したいのか、これらをはっきりさせることが第一です。
それが分かれば、元信号とサンプリング周波数は自ずと仕様が決まることが多いです。
しかしいずれにせよ、ノイズの仕様というか特徴は分かっていないわけです。
そして、フィルタの仕様を決めるためには、周波数で見たノイズの特徴を見つけなければなりません。
そこで登場するのがフーリエ解析です。
普通、信号処理の教科書を見るとおそらく最初のトピックはほとんどがフーリエ解析だと思います。が、すみません本シリーズではなかなか登場させる機会が無く、最後のSTEPでの紹介になってしまいました。
フーリエ変換
このシリーズは直感的な理解をモットーとしているためフーリエ解析の理論的な内容は省略して、あくまで便利なツールとしての紹介に留めます。
なので以降フーリエ解析とは呼ばず、全てひっくるめてフーリエ変換で統一します。
まずはやってみましょう。
さて、先程のノイズがのった信号を再掲します。
もちろんこの信号を見るだけでは、ノイズの周波数的な特徴は分かりません。
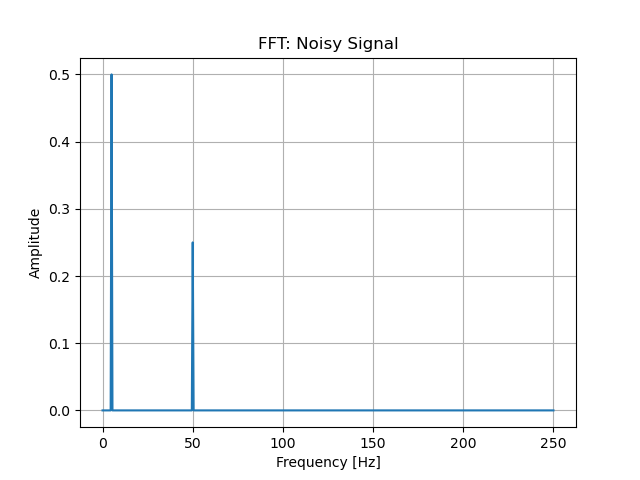
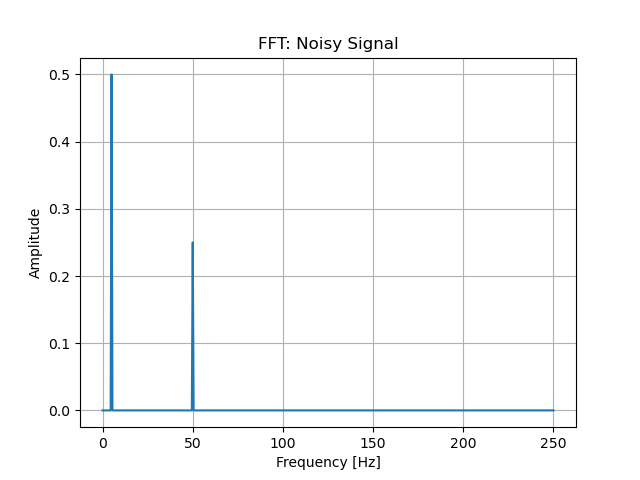
そこでこれをフーリエ変換してみると、、、
こんな感じで結果が出てきます。
それぞれのグラフの横軸をみてほしいんですが、一つ目の信号はTime[s]で時間です。
一方で、二つ目のフーリエ変換結果の図は横軸がFrequency[Hz]で周波数です。
つまり、フーリエ変換した結果、時間軸上で見ていた信号を周波数領域で見ることができるようになったということです。
そしてフーリエ変換結果の縦軸は該当する横軸の周波数成分の大きさです。すなわち、今回この信号には5Hzと50Hzにあたる周波数成分が含まれているということが分かります。
※余談ですが、実用上はほとんどの場合、高速フーリエ変換(FFT:Fast Fourier Transform) という、高速計算アルゴリズムを使用します。
実は、この周波数領域へ移すという操作はすでにやったことがあります。
そう、伝達関数$H(z)$を周波数領域に当てはめるとき、$z=e^{jω}$を代入することで周波数領域でのフィルタの伝達関数$H(e^{jω})$を求めていましたね。
あの時はいきなりz変換が出てきましたが、あらためてまとめると下記になります。
<周波数領域での伝達関数の出し方>
(1):STEP3での方法
・インパルス応答
↓ z変換
・伝達関数$H(z)$
↓ $z=e^{jω}$を代入
・伝達関数$H(e^{jω})$
しかし、フーリエ変換を使っても同じことができます。
(2):フーリエ変換を使った方法
・インパルス応答
↓ フーリエ変換
・伝達関数$H(e^{jω})$
すなわち、インパルス応答のz変換は伝達関数$H(z)$、フーリエ変換は伝達関数$H(e^{jω})$ということができ、さらに伝達関数$H(z)$に$z=e^{jω}$を代入すると伝達関数$H(e^{jω})$になります。
考え方としては、伝達関数$H(z)$の方が一般化された表現方法で、伝達関数$H(e^{jω})$はその中でも実信号を扱う際の表現方法というのが分かりやすいかと思います。
あらためて、今回の信号には5Hzと50Hzに該当する周波数成分が含まれています。
そして信号の仕様としては下記のようになっていたので、ノイズの周波数は5Hzでない方の周波数成分、つまり50Hzであるということができます。
・元信号:5Hzの正弦波
・ノイズ:?⇒ 50Hz
・サンプリング周波数:500Hz
それではここまででノイズ解析ができたので、ここからフィルタ設計に入ります。
3. フィルタ設計
フィルタに必要な仕様を考えてみましょう。
元信号は5Hzです。ノイズは50Hzでそれ以外の周波数成分は信号に含まれていません。
なので、この場合は元信号とノイズの周波数が十分に離れています。
元信号とノイズが周波数的に分離しているのであれば、ある周波数を基準にして、そこより高いor低い周波数成分を除去するようなフィルタを設計するのが良い方法となります。
これはフィルタ設計の定石のようなものですが、特定の帯域だけを残して他を全て除去するとか、逆に狭い帯域をピンポイントで除去するとか、操作したい周波数帯域を狭めるほど、フィルタ設計は難しく複雑になる傾向があります。
よって今回は20Hzを基準にして、それ以上の周波数成分を除去するローパスフィルタを設計しましょう。このとき基準になる周波数をカットオフ周波数と呼びます。
※補足ですが逆に基準以下の周波数を除去するフィルタはハイパスフィルタと呼ばれます。
信号の仕様にフィルタの仕様を付け加えてまとめると、下記になります。
・元信号:5Hzの正弦波
・ノイズ:50Hz
・サンプリング周波数:500Hz
・フィルタ仕様:20Hzをカットオフ周波数とするローパスフィルタ
さて、フィルタ仕様が決まったのでいよいよ設計です。
とはいえ何も難しいことはなく、ただPythonやMATLABを使用して関数を呼ぶだけです。
実際のプログラムは別記事にまとめるので、設計の結果だけ表示します。
比較のためFIRフィルタとIIRフィルタの両方を設計しました。
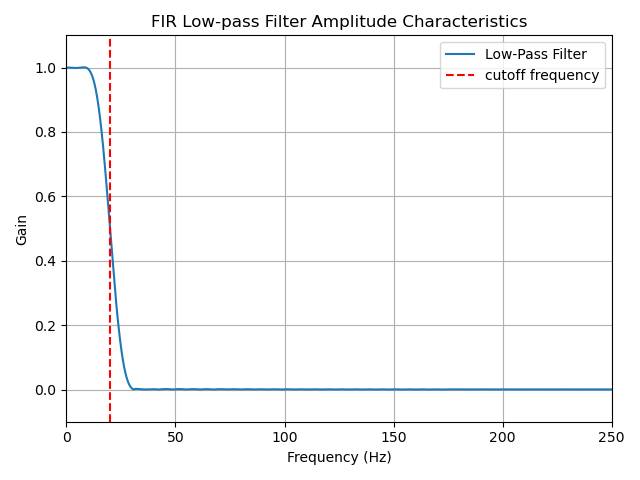
<設計したFIRフィルタ>
・振幅特性
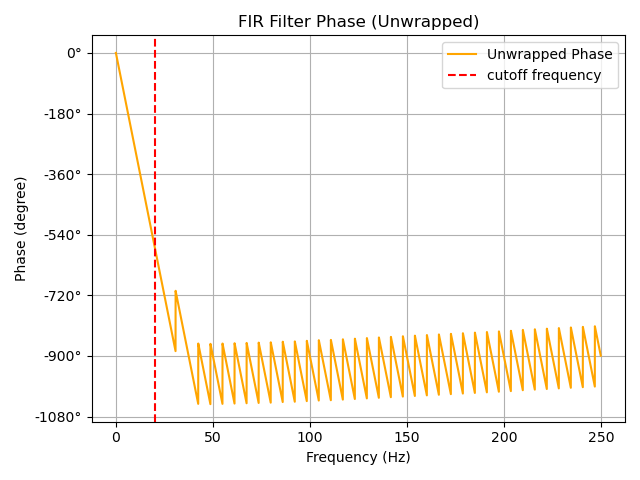
・位相特性(アンラップしています)
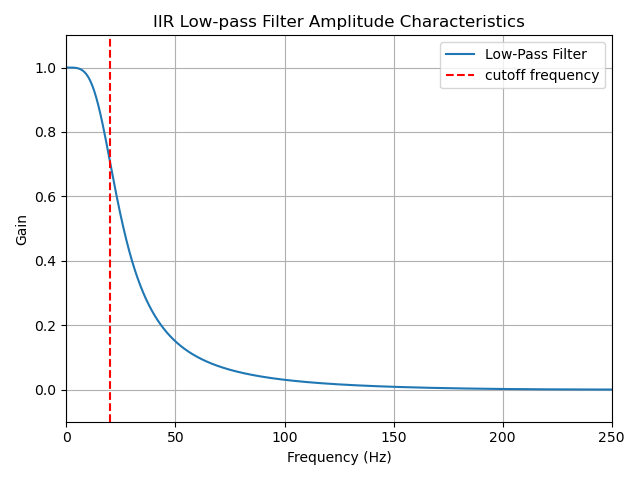
<設計したIIRフィルタ>
・振幅特性
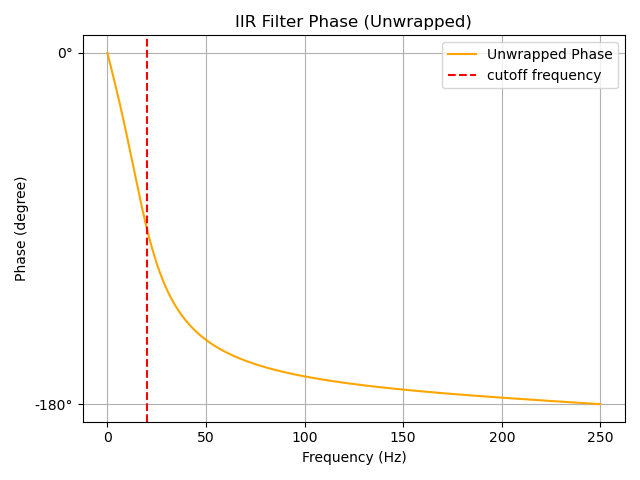
・位相特性(アンラップしています)
FIR/IIRそれぞれの振幅特性を見ると、FIRフィルタの方は50Hzでゲインが0になっているのに対して、IIRフィルタの方は0.17程度のゲインがあります。
すなわち、今回の信号におけるノイズ=50Hzの信号除去能力はたった今設計したフィルタを比較するとFIRフィルタの方が高いと言えます。
続いて群遅延とステップ応答時間についても見ていきましょう。
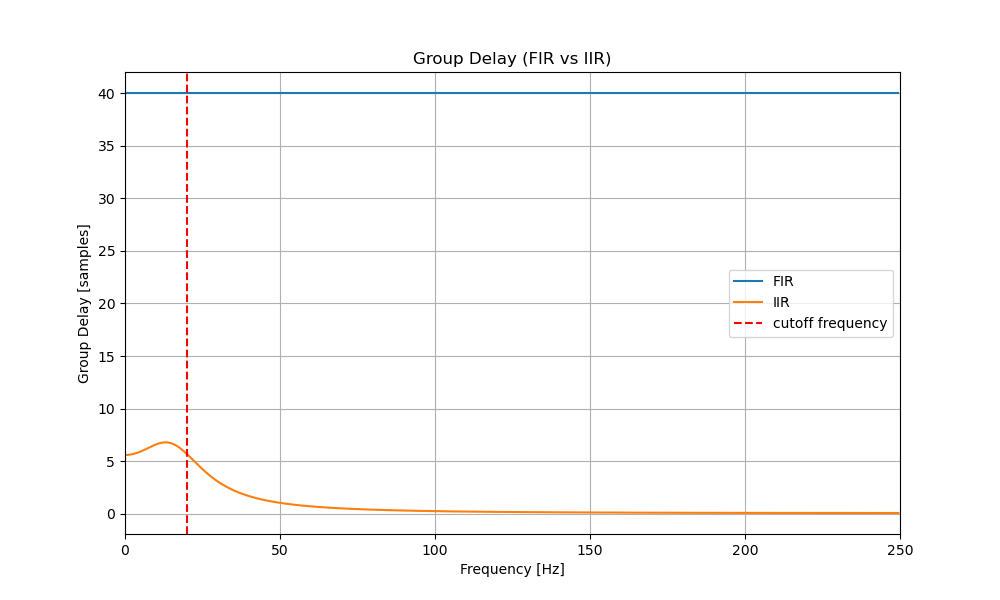
・群遅延
・ステップ応答時間
群遅延は非線形性を持っていますが、IIRフィルタの方が小さいですね。つまり、波形が歪んでも構わないようなアプリケーションではIIRフィルタの方が有利と言えるでしょう。
また、ステップ応答時間は圧倒的にIIRフィルタの方が短いですね。値の収束もIIRフィルタが有利と言えそうです。
それでは、作成した信号に両フィルタを適用した結果を確認してみましょう。
4. 結果確認
ノイズの重畳した元信号を再掲します。
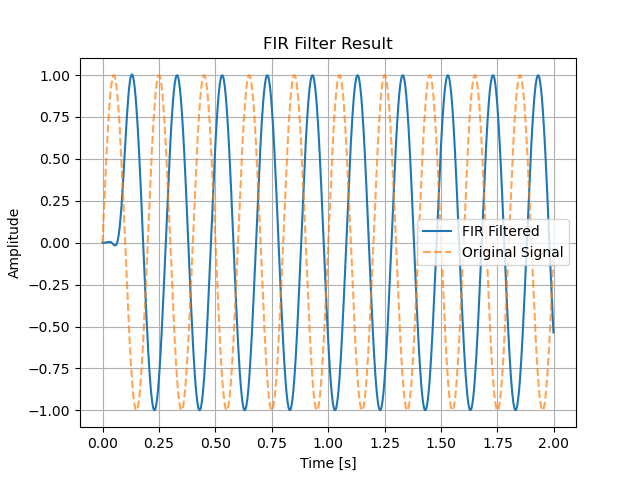
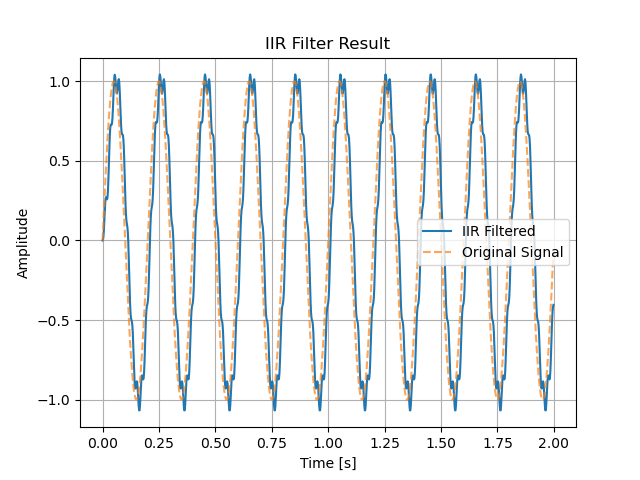
ここにフィルタを適用した結果です。
前節で確認したフィルタの特性を再度下記に示します。
・ノイズ除去性能:FIR > IIR FIRフィルタの方が高い
・群遅延による波形歪み:FIR > IIR FIRフィルタの方が波形歪みがない
・群遅延による遅れ時間:FIR < IIR IIRフィルタの方が遅れ時間が小さい
・ステップ応答時間:FIR < IIR IIRフィルタの方が遅れ時間が小さい
どうでしょうか?フィルタ適用後の信号は上記フィルタ特性の通りになっていますね。
加えて、周波数軸上でもフィルタ適用後の信号を見てみましょう。
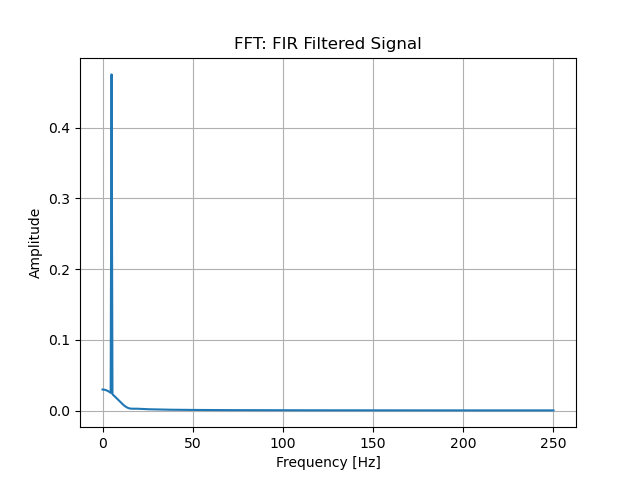
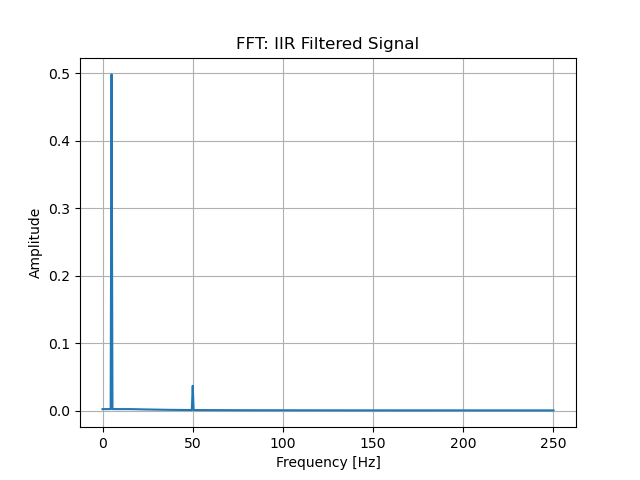
フィルタ適用後の信号をフーリエ変換して。周波数ごとの成分の大きさを調べます。
FIRフィルタ適用後の信号は50Hzの成分がきれいに消えていますが、IIRフィルタを適用した信号は50Hzの成分が残っています。
よって周波数領域で見ても、今回設計したフィルタに関して言えばノイズ除去性能がFIR>IIRであることが分かります。
ここでもうひとつ大事なことですが、周波数領域で見ると群遅延やステップ応答時間のようなフィルタの時間的特性は表現できていませんよね。
何が言いたいかというと、信号の性質は一面で見ると分からないことが多いため、時間軸上と周波数領域の両方できちんと確認することが大切だということです。
まとめ
今回はノイズ除去実践編としてノイズの重畳したシミュレーション用信号を作成し、ノイズ解析とフィルタ設計、結果確認までを行いました。
本シリーズはこれで終了ですが、続編としてアプリケーションごとの具体的なフィルタ設計例を公開予定です。公開したらリンクを貼りますので、また見ていただけると嬉しいです。