はじめに
・キッチンスケールで小麦粉の重さを量る
・Bluetoothイヤホンで音楽を聴く
・GPSで今いる場所を確認する
これら全ての基礎になる技術が信号処理です。
そして信号処理で扱うあらゆる信号には影のようにつきまとってくるものがあります。
そう、ノイズですね。
・電源ラインから入り込んでくるノイズ
・モータの振動によるノイズ
・電子回路のクロストークノイズ
原因は様々ですが通常、信号とノイズは必ずセットで扱わなければなりません。
最も有効なノイズ対策はノイズ源そのものを除去することですが、例えば工場での重量計測において、計測中は周囲で動いてる装置を全部止めて振動を無くしましょう!なんて現実的ではありません。
そこで活躍するのがフィルタ技術、とりわけデジタル(ディジタル)フィルタです。
このシリーズではフィルタ設計法習得に向け、フィルタ設計と信号処理の基礎に関する直感的な理解を目標に解説していきたいと思います。
なるべく数式を排して取っつきやすい説明を行っていくつもりなので、やや不自然な言い回しや誤解を招きかねない表現があるかもしれません。
そういった箇所を見つけられた場合はすみませんが、ご指摘頂けると幸いです。
本記事はその STEP3:周波数領域における伝達関数 です。
他STEPへのリンクは下記です↓
STEP:0 導入編
STEP:1 フィルタ特性の見方
STEP:2 インパルス応答とフィルタ
STEP:4 ノイズ除去実践編
簡単なフィルタ設計&性能評価をやってみたい方は下記もどうぞ↓
FIRローパスフィルタを作ってみよう!
1. 前回のおさらい
前回はインパルス応答と伝達関数について説明しました。
おさらいとして、下記に簡単にまとめてみます。
<インパルス信号>
下記図のように時刻 n=0のときだけ"1"、その他は0になるような信号をインパルス信号と呼びます。
このインパルス信号を何かしらの 「システム」に入力したとき、そのシステムがどんな出力信号を出すか、言い換えるとシステムがどんな応答を返すかをインパルス応答と呼びます。
理想的にはインパルス信号には直流成分から超高周波な成分まで、あらゆる周波数成分が等しい大きさで含まれているので、出力信号もあらゆる周波数成分に対する出力になります。
よって、インパルス応答が分かる = 各周波数における出力特性が分かるということです。
インパルス応答はインパルス信号を入力したシステムのふるまいによって、応答が継続する時間が変化します。
継続する時間が有限であれば、有限インパルス応答、無限であれば無限インパルス応答と呼ばれます。
有限インパルス応答>
この場合はインパルス応答はn=3で0に収束していますね。
<無限インパルス応答>
この場合インパルス応答は小さくなっていくものの0には収束せず、n=20でもまだ続いています。実用上、計算機の扱える桁数には制限があるためいずれは0として扱われることになりますが、理論上は無限に続きます。
<伝達関数>
フィルタへの入力値$X(z)$と出力値$Y(z)$の比を$H(z)$と表すと、$H(z)$は下記になります。
$$
H(z) = \frac{Y(z)}{X(z)}
$$
こういう入出力の比で表される$H(z)$を制御工学や信号処理では伝達関数と呼びます。
<FIRフィルタの伝達関数>
$$
H(z) = \frac{Y(z)}{X(z)} = \sum_{n=0}^{N} b_n z^{-n}
$$
すなわち、FIRフィルタは入力信号のみを使って出力を決定します。
<IIRフィルタの伝達関数>
$$
H(z) = \frac{Y(z)}{X(z)} = \frac{(\sum_{n=0}^{N} b_n z^{-n})}{(1 + \sum_{n=1}^{M} a_n z^{-n})}
$$
IIRフィルタは入力信号に加えて過去の出力をフィードバックして出力を決定します。
インパルス応答と伝達関数は本質的には入出力関係という、同じものを指しています。
フィルタの伝達関数が分かれば、入力に対する出力を求めることができるようになります。
しかし、上記のインパルス応答は時間軸上でのお話で、この後に出てきますが伝達関数はそのz変換です。しかし、これまでの記事ではフィルタの振幅・位相特性はどちらも周波数軸上で見てきたはずです。
よって、インパルス応答や伝達関数を周波数軸上で当てはめるにはどうすれば良いのか?と疑問が生じると思います。
以下、その疑問の答えを含めて解説していきます。
2. 遅延演算子と周波数
前回導入した$z$ですが、これを導入した目的は現時刻から見てn回前の入出力を$z^{-n}$と置くことで、伝達関数やフィルタの入出力関係を代数的に記述しやすくすることでした。
この$z$は実はきちんと名前があって、n時刻前にシフトしていることを$z^{-n}$と書くやり方も、私が勝手に決めたものではありません。
$z$は制御工学や信号処理において、シフト演算子や遅延演算子 と呼ばれるもので、離散信号すなわちデジタルな信号を扱う際に用いられるz変換 というものが元になっています。
細かい説明は省きますが、z変換と離散時間フーリエ変換の定義から、$z$は$z=e^{jω}$と置き換えることができます。 $e^{jω}$には$ω$が含まれていますが、これは角周波数を$ω$と表しています。念のため、$j$は虚数単位です。
ということは、$z$を使った伝達関数も$z=e^{jω}$を代入すれば周波数を含んだ形で取り扱うことができますね。
さっそく、FIRフィルタとIIRフィルタの伝達関数を周波数を含んだ形に書き直してみます。
・FIRフィルタ
$$
zを含む形: H(z) = \sum_{n=0}^{N} b_n z^{-n}
$$
$$
ωを含む形: H(e^{jω}) = \sum_{n=0}^{N} b_n e^{-jωn}
$$
・IIRフィルタ
$$
zを含む形: H(z) = \frac{(\sum_{n=0}^{N} b_n z^{-n})}{(1 + \sum_{n=1}^{M} a_n z^{-n})}
$$
$$
ωを含む形: H(e^{jω}) = \frac{(\sum_{n=0}^{N} b_n e^{-jωn})}{(1 + \sum_{n=1}^{M} a_n e^{-jωn})}
$$
ちなみに角周波数$ω$(単位はrad/secです)と周波数$f$(Hz)の間は$ω=2πf$の関係なので、$e^{jω}=e^{j2πf}$と書くこともできます。
この伝達関数を用いることでようやく、定量的なフィルタの振る舞いを周波数軸上で解析することができます!
3. 伝達関数によるフィルタの解析
それでは前節で導いた周波数を含む形での伝達関数を用いて、改めてフィルタの周波数特性を考えていきましょう。
フィルタの周波数特性は2種類に分けられました。
そう、振幅特性と位相特性ですね。これまではそれぞれの特性をグラフから何となく読み取っていましたが、もうそんなことをする必要はありません。
グラフから読み取らなくても、
![]()
$$
H(e^{jω}) = \sum_{n=0}^{N} b_n e^{-jωn}
$$
伝達関数で全てが分かる!
伝達関数を$H(e^{jω})$としたとき、フィルタの振幅特性と位相特性は下記の通りです。
$$
振幅特性 : |H(e^{jω})|
$$
$$位相特性:\angle H(e^{jω})
$$
どうでしょうか?非常にシンプルに表現できますね。
振幅特性は伝達関数の絶対値、位相特性は伝達関数の偏角ということです。
※ちなみに、もちろんこれはFIRフィルタ/IIRフィルタ関係無く同じ式になります。
しかし、実際に手計算で伝達関数から絶対値や偏角を求めるというのはなかなか面倒です。通常はプログラムを書いて、コンピュータに計算してもらう方が良いですね。
PythonにせよMATLABにせよ、ありがたいことに関数一発で出来ます。
4. 群遅延とステップ応答時間
さて、次にフィルタの遅延時間、または応答遅れはどうやって定量化されるのでしょうか?
長いこと積み残してきましたが、いよいよこの疑問に答えていきましょう。
群遅延
STEP2で線形位相特性を持つフィルタに信号を通しても波形はその形を保つ一方で、非線形位相特性を持つフィルタに信号を通すと位相変化の非線形性により波形が歪む、ということを説明しました。
ここで線形位相/非線形位相に関わらず、各周波数の信号がどれくらい遅れるかを定量化する指標として、群遅延について解説します。
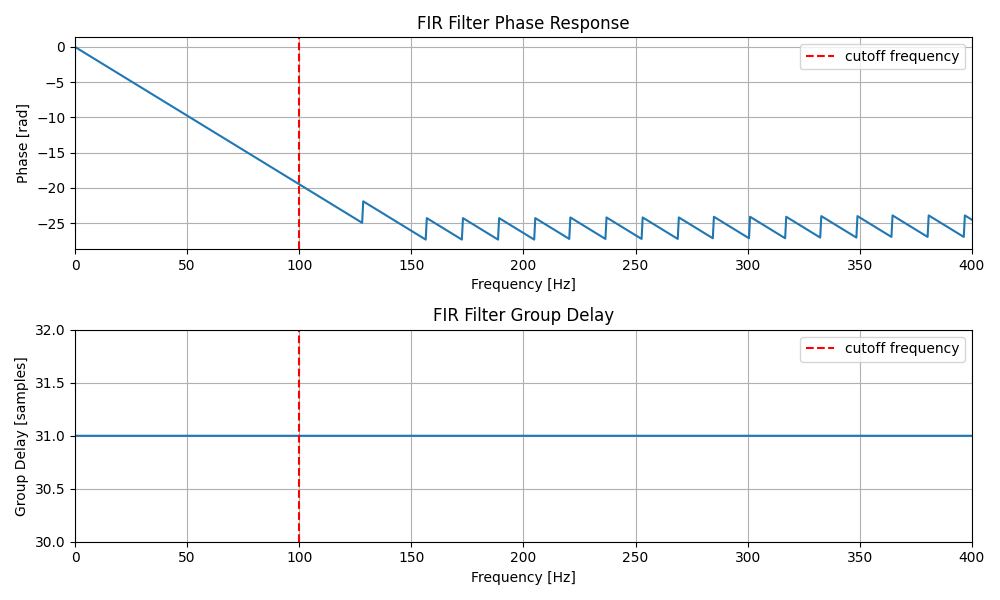
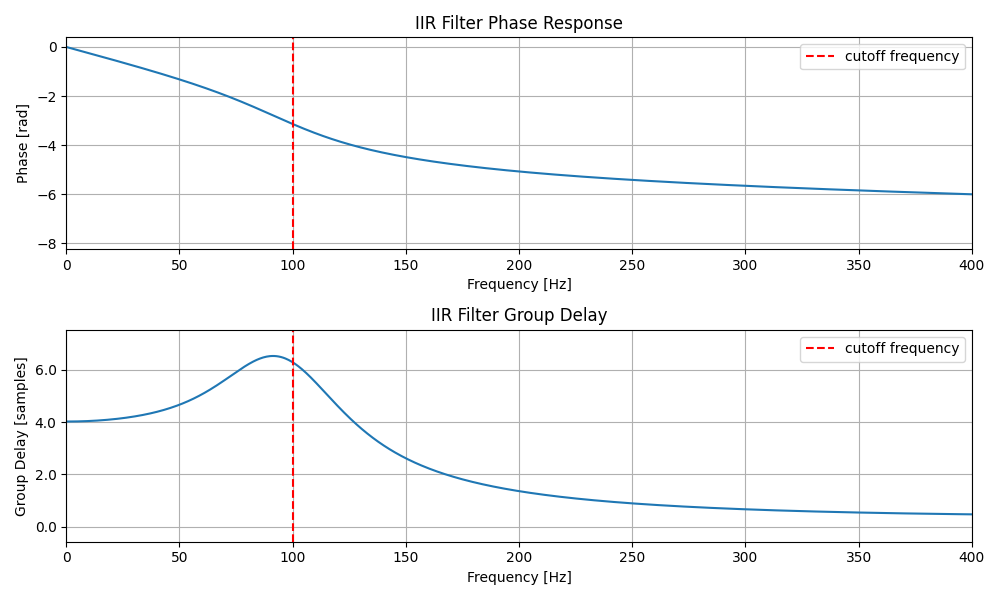
まず下記図を見てください。それぞれ上段に位相特性、下段に群遅延を記載しています。
<FIRフィルタの位相特性と群遅延>
FIRフィルタが線形位相特性、IIRフィルタが非線形位相特性を持つことすでに説明しました。ここで各フィルタの下段に示した群遅延を見ると、FIRフィルタはまっすぐな線ですがIIRフィルタは周波数ごとに大きく変化していることが分かります。
群遅延の定義式を次に示します。
$$
群遅延 = -\frac{d}{dω}\angle H(e^{jω})
$$
式から読み取れるように、群遅延は位相特性を周波数ごとに微分したものです。
言い換えると、各周波数成分に対する位相変化の傾きを表しています。
線形位相特性を持つフィルタであれば位相変化の傾きは当然一定のため、すなわち群遅延も一定です。これがFIRフィルタの群遅延がまっすぐな線になっている理由です。
一方で、非線形位相特性を持つフィルタであれば、位相変化の傾きに応じて群遅延が変化します。よって、IIRフィルタでは群遅延も周波数ごとに変化しています。
群遅延の直感的な意味としてはフィルタを通ることによる時間的な遅れを周波数成分ごとにプロットしたものと考えると、理解しやすいかと思います。
フィルタを通ることによる、信号の時間的な遅れのひとつ目はこの群遅延です。そして先程示した定義式によって、群遅延による時間的な遅れは定量化できますね!
ステップ応答時間
群遅延はフィルタの周波数ごとの時間的な遅れを表現し、フィルタを通ることによる信号の遅延を表していることは間違いないです。
しかし、例えば重量計測のようにフィルタを通して得たい信号が直流成分、すなわち定常的な値である場合は群遅延よりもステップ応答時間を用いて時間的な遅れを表した方が都合が良いことがあります。
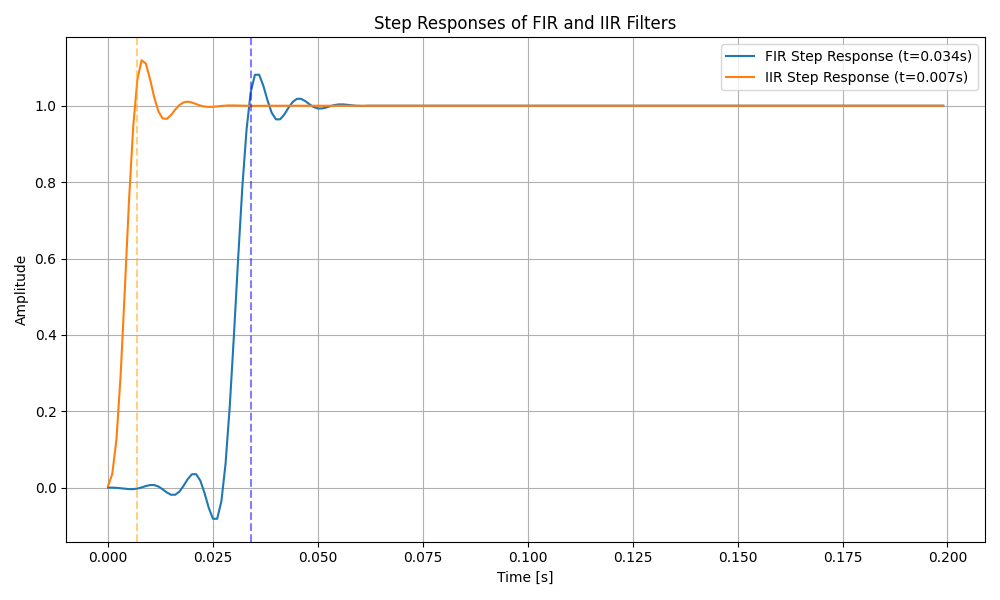
まず図を出します。FIRフィルタとIIRフィルタにステップ入力を与えた場合の出力です。
※ステップ入力は0時刻目から立ち上がって以降、ずっと1が続くような信号です。
<FIRフィルタとIIRフィルタのステップ応答>
ステップ入力を受けて、出力が98%に達するまでの時間をグラフ中に示しています。
この場合はFIRフィルタが0.034(sec)、IIRフィルタが0.007(sec)とIIRフィルタの方が早く出力が収束していますね。
ステップ応答時間の求め方ですが、群遅延とは異なりFIRフィルタとIIRフィルタでちょっと違います。
FIRフィルタの方から考えてみましょう。
伝達関数はこうでしたね。
$$
H(e^{jω}) = \sum_{n=0}^{N} b_n e^{-jωn}
$$
いまさらですがこの式を時間軸上で考えた場合、「出力がn=0からNまでのインパルス応答の累積和で構成されている」、ということを意味します。
裏を返せば、「累積和が取れるまでちゃんとした出力が出てこない」とも言い換えることができます。
通常「n=0からNまで」のnの個数、すなわち「N+1」のことをフィルタ次数とかタップ数、フィルタ長と呼びます。
すなわち、ステップ応答時間=ちゃんとした出力が出てくるまでの時間は累積和が取れるまでの時間によって変化し、その時間はフィルタ次数に依存します。
なので結局、秒としてのFIRフィルタの最大ステップ応答時間は下記によって求められます。
$$
FIRフィルタのステップ応答時間 ≈ フィルタ次数×(サンプリング周期 / 2)
$$
※厳密には完全に一致はしませんが、実用上は上記の式で考えて良いです。
※設計によって、実質的にはもっと速く収束することもあり得ます。
次にIIRフィルタの場合を考えてみましょう。
伝達関数は下記です。
$$
H(e^{jω}) = \frac{(\sum_{n=0}^{N} b_n e^{-jωn})}{(1 + \sum_{n=1}^{M} a_n e^{-jωn})}
$$
この伝達関数を見て無限インパルス応答について思い出してほしいんですが、IIRフィルタの場合は出力のフィードバックがあるために、インパルス応答が(理論上)無限に継続し、収束しないのでした。
つまり、FIRフィルタと同じようにフィルタ次数のみでステップ応答時間を求めることはできません。
しかし同時に、収束しないというのはあくまで理論上の話であって実際のインパルス応答は指数関数的に減衰していくわけです。
よって、IIRフィルタの場合は「ステップ入力を受けて、出力が99%に達するまで」等の閾値を設けて、近似的にステップ応答時間を求めます。
近似する方法として、理論的には伝達関数の極配置から求める方法等ありますが、実用上は実際に信号をIIRフィルタに通して実測するのが手っ取り早いですね。
よって、IIRフィルタのステップ応答時間は書くとしたら下記のようになります。
$$
IIRフィルタのステップ応答時間 ≈ インパルス応答の収束時間(定義や近似方法は様々)
$$
フィルタの遅延時間について
さて、ここまで群遅延とステップ応答時間からフィルタの遅延時間について定量化を行ってきたわけですが、一般的な意味で「フィルタの応答遅れ」というと、ステップ応答時間の方が直感的に理解しやすいと思います。
ですが、例えば通信分野ではデータ誤りを防ぐために波形を歪ませないことが重要なため、群遅延がステップ応答時間より重視されますし、重量のような定常値を計測するアプリケーションでは計測を速く終えるために、ステップ応答時間が群遅延より重視されます。
結局は信号処理をどんなアプリケーションに適用するかによって重視する特性を理解し、使い分けられるようにしておくことが重要ということですね。
まとめ
今回は伝達関数の周波数領域での表現方法と、それを利用したフィルタの振幅特性及び位相特性の求め方について説明しました。
また、フィルタの遅延時間に関して群遅延とステップ応答時間という2種類の時間的な遅れを示し、伝達関数を用いたそれぞれの定量化を行いました。
ここまで理解できればフィルタの入出力関係の周波数領域での解析と、それを時間軸に移して実際にマイコンやPCに実装したフィルタと性能比較/評価を行うことができるようになっているはずです。
このシリーズは次回を最終回とします。
最終回は実践編として、信号のノイズ解析・フィルタ設計・結果確認までを実際に試してみましょう。