はじめに
下記シリーズ記事で信号処理の基礎的な内容とフィルタについて説明しました。
直感的に理解する信号処理とフィルタ
が、やっぱり直接動かして触って遊ばないと面白くないので、PythonでFIRローパスフィルタを設計するコードと、設計したフィルタを時系列信号に適用するコードを用意しました。
GUI上からパラメータを振れるようになっているので、いろいろと触って動かしてもらえたら良いかなと思います。
本文中のコードを上から順にコピペしてもらっても動きますが、
GitHubにもコードその他を置いています。
GitHub FIR_Samples
zennに移動平均フィルタに関する記事をあげました。ご興味あればご覧ください!
どこをカットする?周波数特性から見る移動平均フィルタ
設計アルゴリズムの簡単な解説
一応、解説を入れます。良ければ目を通してください。
本スクリプトで選べる設計アルゴリズムは4種類です。
すなわち、
(1):フーリエ変換法
(2):窓関数法
(3):最小二乗法
(4):Parks-McClellan法(Remezアルゴリズム)
(1)と(2)はインパルス応答からフィルタを設計しようという考え方です。
インパルス応答のフーリエ変換は周波数特性なので、インパルス応答をうまく設計してやれば周波数領域ではフィルタとして機能するだろう、ということです。
しかし、細かい説明は省きますがインパルス応答を設計してフィルタとして用いようとする場合、理想的なインパルス応答は無限に続くため、実際のところはそれを有限で打ち切った形になります。
よって、設計したインパルス応答は理想的な応答の近似になるため誤差が生じます。
(3)と(4)はインパルス応答を周波数領域に持っていくのではなく、初めから周波数領域で理想的な特性を近似しようとするアルゴリズムです。
最小二乗法は理想的な周波数特性を近似するようなインパルス応答を、最小二乗法を用いて周波数領域で求めます。
なので、周波数特性全体で見た時に誤差のエネルギーが最小になるような設計ができます。
つまり、出来る限り最高の特性を持てるケースを実現しようとするアルゴリズムです。
一方で、Parks-McClellan法は同じように周波数領域で理想的な特性を近似しようとしますが、周波数全体をいくつかのブロックに分けて、各ブロックの誤差を比較して最大の誤差を最小化するような設計を行います。
つまり、最悪のケースにおける誤差をできる限り小さくしようとするアルゴリズムです。
高精度な計測用途では誤差のコントロールがしやすい、設計に融通が利きやすい等の利点があることから主に(3)、(4)のアルゴリズムが使用されることが多いです。
とまあ、なんやかんや理屈はあるんですが、とりあえず試して特性を見てもらうのが何より一番分かりやすいと思います!
FIRローパスフィルタの設計用 Pythonコード
環境は以下の通りです。
・Python:3.8~3.12
・numpy:1.20~
・scipy:1.4.0~
・matplotlib:3.0~
import tkinter as tk
from tkinter import ttk, filedialog
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import csv
とりあえずフィルタの設計を行います。
def design_fir_filter():
try:
cutoff = float(entry_cutoff.get())
fs = float(entry_fs.get())
numtaps = int(entry_tap.get())
pass_gain = float(entry_pass_gain.get())
stop_gain = float(entry_stop_gain.get())
method = combo_method.get()
nyq = fs / 2
if cutoff <= 0 or cutoff >= nyq:
raise ValueError("カットオフ周波数は0より大きく、(サンプリング周波数 / 2)未満 にしてください")
if numtaps <= 0 or numtaps >= int(fs*2):
raise ValueError("フィルタ次数はサンプリング周波数 * 2未満にしてください")
if method == "窓関数法":
coeffs = signal.firwin(numtaps, cutoff, window="hamming", fs=fs, pass_zero='lowpass')
elif method == "フーリエ変換法":
freqs = [0, cutoff, cutoff + 0.05 * fs, nyq]
gains = [pass_gain, pass_gain, stop_gain, stop_gain]
coeffs = signal.firwin2(numtaps, freqs, gains, fs=fs)
elif method == "最小二乗法":
bands = [0, cutoff, cutoff + 0.05 * fs, nyq]
desired = [pass_gain, pass_gain, stop_gain, stop_gain]
coeffs = signal.firls(numtaps, bands, desired, fs=fs)
elif method == "Remez":
bands = [0, cutoff, cutoff + 0.05 * fs, nyq]
desired = [pass_gain, stop_gain]
coeffs = signal.remez(numtaps, bands, desired, fs=fs)
else:
raise ValueError("無効なアルゴリズム選択です")
↑の続きで、設計したフィルタの特性表示です。
# 周波数応答プロット
w, h = signal.freqz(coeffs, worN=8000, fs=fs)
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(w, 20 * np.log10(np.abs(h)))
plt.title("Frequency Response")
plt.xlabel("Frequency [Hz]")
plt.ylabel("Amplitude [dB]")
plt.grid(True)
plt.ylim(-100, 5)
# インパルス応答プロット
plt.subplot(1, 2, 2)
plt.stem(coeffs)
plt.title("Impulse Response")
plt.xlabel("Taps")
plt.ylabel("Amplitude")
plt.grid(True)
plt.tight_layout()
# 位相特性とステップ応答時間のグラフ化
fig2, axs2 = plt.subplots(1, 2, figsize=(10, 4))
# 位相特性
phase = np.unwrap(np.angle(h)) # 位相をアンラップ
axs2[0].plot(w, np.degrees(phase))
axs2[0].set_title("Phase Response")
axs2[0].set_xlabel("Frequency [Hz]")
axs2[0].set_ylabel("Phase [degrees]")
axs2[0].grid(True)
# ステップ応答
step = np.cumsum(coeffs) # FIRのステップ応答はインパルス応答の積分
axs2[1].plot(np.arange(len(step)) / fs, step)
axs2[1].set_title("Step Response")
axs2[1].set_xlabel("Time [s]")
axs2[1].set_ylabel("Amplitude")
axs2[1].grid(True)
# 99%到達時間の計算
threshold = 0.99 * step[-1]
idx_99 = np.argmax(step >= threshold)
t_99 = idx_99 / fs
axs2[1].axvline(t_99, color='r', linestyle='--', label=f"99% at {t_99:.4f} s")
axs2[1].legend()
fig2.tight_layout()
plt.show()
# 保存用に係数をグローバルに保存
global last_coeffs
last_coeffs = coeffs
lbl_result["text"] = "フィルタ設計成功!"
except ValueError as e:
lbl_result["text"] = f"エラー: {str(e)}"
設計結果の保存です。
def save_coeffs():
if last_coeffs is None:
lbl_result["text"] = "設計したフィルタがありません"
return
filepath = filedialog.asksaveasfilename(defaultextension=".csv", filetypes=[("CSV files", "*.csv")])
if filepath:
with open(filepath, "w", newline="") as f:
writer = csv.writer(f)
for c in last_coeffs:
writer.writerow([c])
lbl_result["text"] = f"係数を保存しました: {filepath}"
GUIから動かせるようにしています。
# GUIセットアップ
root = tk.Tk()
root.title("FIRローパスフィルタ設計")
tk.Label(root, text="サンプリング周波数 [Hz]:").grid(row=0, column=0, padx=10, pady=5)
entry_fs = tk.Entry(root)
entry_fs.insert(0, "1000")
entry_fs.grid(row=0, column=1, padx=10, pady=5)
tk.Label(root, text="カットオフ周波数 [Hz]:").grid(row=1, column=0, padx=10, pady=5)
entry_cutoff = tk.Entry(root)
entry_cutoff.insert(0, "200")
entry_cutoff.grid(row=1, column=1, padx=10, pady=5)
tk.Label(root, text="フィルタ次数:").grid(row=2, column=0, padx=10, pady=5)
entry_tap = tk.Entry(root)
entry_tap.insert(0, "101")
entry_tap.grid(row=2, column=1, padx=10, pady=5)
tk.Label(root, text="通過帯域ゲイン:").grid(row=3, column=0, padx=10, pady=5)
entry_pass_gain = tk.Entry(root)
entry_pass_gain.insert(0, "1")
entry_pass_gain.grid(row=3, column=1, padx=10, pady=5)
tk.Label(root, text="阻止帯域ゲイン:").grid(row=4, column=0, padx=10, pady=5)
entry_stop_gain = tk.Entry(root)
entry_stop_gain.insert(0, "0")
entry_stop_gain.grid(row=4, column=1, padx=10, pady=5)
tk.Label(root, text="設計アルゴリズム:").grid(row=5, column=0, padx=10, pady=5)
combo_method = ttk.Combobox(root, values=["窓関数法", "フーリエ変換法", "最小二乗法", "Remez"])
combo_method.grid(row=5, column=1, padx=10, pady=5)
combo_method.current(0)
btn_design = tk.Button(root, text="設計して表示", command=design_fir_filter)
btn_design.grid(row=6, column=0, columnspan=2, pady=10)
btn_save = tk.Button(root, text="係数をCSV保存", command=save_coeffs)
btn_save.grid(row=7, column=0, columnspan=2, pady=5)
lbl_result = tk.Label(root, text="")
lbl_result.grid(row=8, column=0, columnspan=2)
last_coeffs = None # 初期化
root.mainloop()
FIRローパスフィルタによるノイズ除去 Pythonコード
せっかく設計したので、csvファイルを読み込んでフィルタリングできるようにしましょう。
環境は同じです。
import tkinter as tk
from tkinter import ttk, filedialog
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import csv
時系列データとフィルタ係数の読み込み用です。
def browse_file(entry_widget):
filepath = filedialog.askopenfilename(filetypes=[("CSV files", "*.csv")])
if filepath:
entry_widget.delete(0, tk.END)
entry_widget.insert(0, filepath)
読み込んだ時系列データにフィルタを適用します。
def apply_filter_to_timeseries():
try:
coeff_path = entry_coeff_path.get()
data_path = entry_data_path.get()
if not coeff_path or not data_path:
raise ValueError("CSVパスが指定されていません")
coeffs = []
with open(coeff_path, newline="") as f:
reader = csv.reader(f)
for row in reader:
coeffs.append(float(row[0]))
time = []
value = []
with open(data_path, newline="") as f:
reader = csv.reader(f)
next(reader) # ヘッダスキップ
for row in reader:
time.append(float(row[0]))
value.append(float(row[1]))
filtered = signal.lfilter(coeffs, [1.0], value)
plt.figure(figsize=(10, 4))
plt.plot(time, value, label="Original")
plt.plot(time, filtered, label="Filtered", linewidth=2)
plt.title("Time Series Filtering Result")
plt.xlabel("Time [s]")
plt.ylabel("Value")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
# 保存
save_path = filedialog.asksaveasfilename(defaultextension=".csv", filetypes=[("CSV files", "*.csv")])
if save_path:
with open(save_path, "w", newline="") as f:
writer = csv.writer(f)
writer.writerow(["time", "value", "filtered_value"])
for t, v, fv in zip(time, value, filtered):
writer.writerow([t, v, fv])
lbl_result["text"] = f"フィルタ結果を保存しました: {save_path}"
except Exception as e:
lbl_result["text"] = f"フィルタ適用エラー: {str(e)}"
こちらもGUIから動作するようにしています。
# GUI setup
root = tk.Tk()
root.title("FIRローパスフィルタ適用")
tk.Label(root, text="係数CSVパス:").grid(row=8, column=0, padx=10, pady=5)
entry_coeff_path = tk.Entry(root, width=40)
entry_coeff_path.grid(row=8, column=1, padx=10, pady=5)
tk.Button(root, text="参照", command=lambda: browse_file(entry_coeff_path)).grid(row=8, column=2)
tk.Label(root, text="時系列CSVパス:").grid(row=9, column=0, padx=10, pady=5)
entry_data_path = tk.Entry(root, width=40)
entry_data_path.grid(row=9, column=1, padx=10, pady=5)
tk.Button(root, text="参照", command=lambda: browse_file(entry_data_path)).grid(row=9, column=2)
btn_apply = tk.Button(root, text="フィルタ適用", command=apply_filter_to_timeseries)
btn_apply.grid(row=10, column=0, columnspan=3, pady=10)
lbl_result = tk.Label(root, text="")
lbl_result.grid(row=11, column=0, columnspan=3)
last_coeffs = None
root.mainloop()
遊び方
<フィルタ設計>
フィルタ設計のスクリプトを動かすと、下記画面になります
基本的にはアルゴリズムを選択して"設計して表示"を押すだけです。
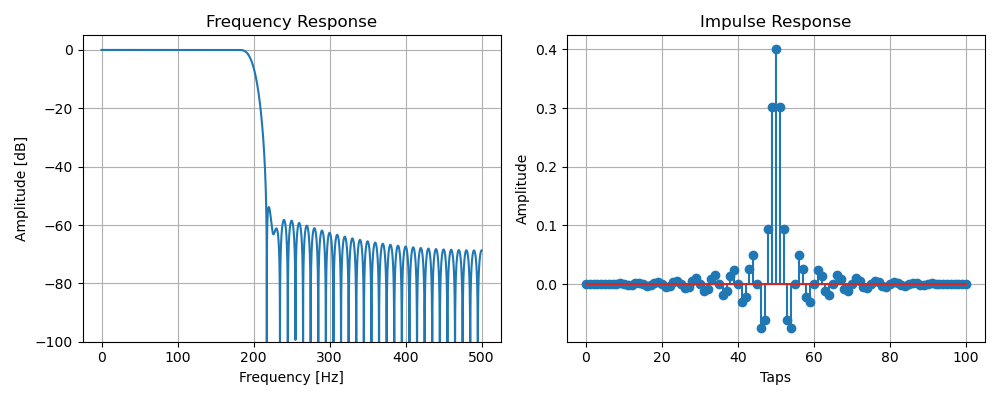
設計できれば振幅特性&インパルス応答と、位相特性&ステップ応答時間が表示されます。
・振幅特性&インパルス応答
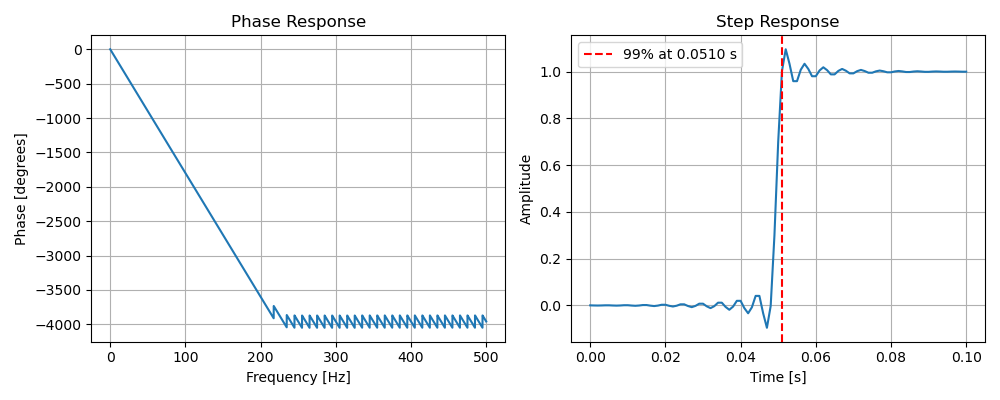
・位相特性&ステップ応答時間 ※位相特性はアンラップしてます
<フィルタ適用>
フィルタ適用のスクリプトを動かすと、下記画面になります。
試しに下記2種類の信号に設計したフィルタを適用してみます。
フィルタのカットオフ周波数:200Hz
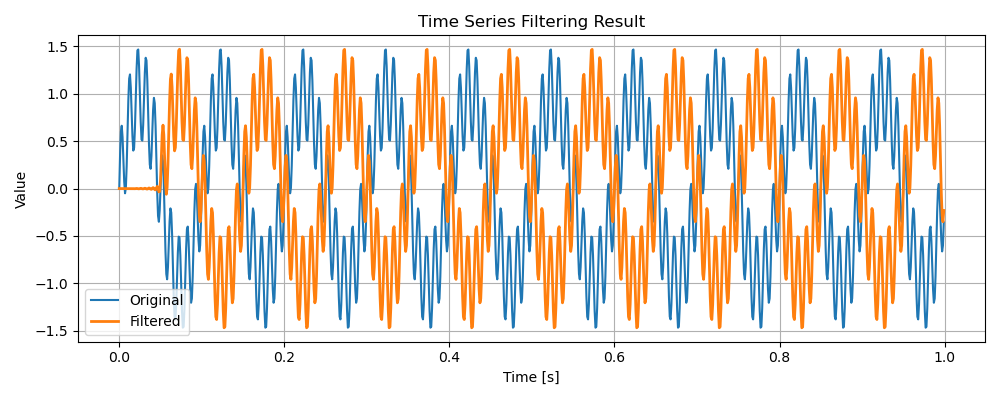
信号(1):元信号10Hzに100Hzのノイズを重畳
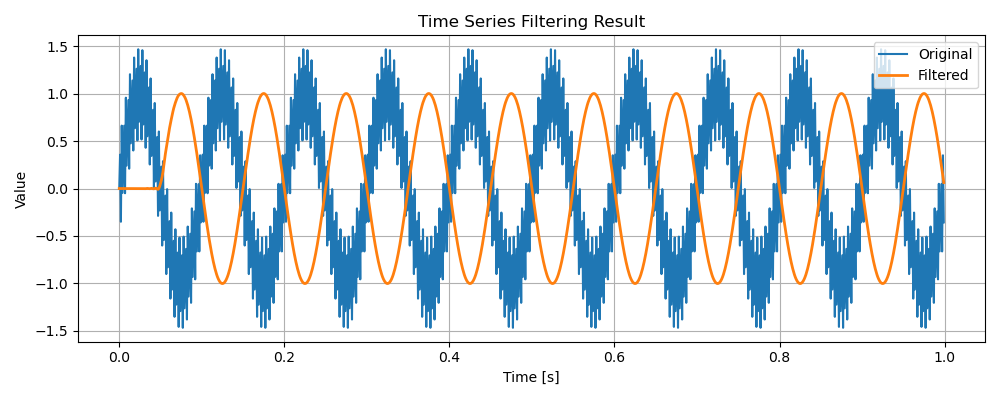
信号(2):元信号10Hzに400Hzのノイズを重畳
・信号(1)
カットオフ周波数よりノイズの周波数が低いので、当然ですがノイズは減っていませんね。
・信号(2)
カットオフ周波数よりノイズの周波数が高いので、きれいにノイズは除去されています。
まとめ
もし自前で取得したセンサの信号とかテスト用信号があれば、是非フィルタ設計&適用して性能評価してみてください。
今回はFIRかつローパスフィルタ限定ですが、別の特性とかIIRの場合も掲載する予定です。
信号処理について興味があれば、下記記事もご覧いただけると嬉しいです!
直感的に理解する信号処理とフィルタ