はじめに
・キッチンスケールで小麦粉の重さを量る
・Bluetoothイヤホンで音楽を聴く
・GPSで今いる場所を確認する
これら全ての基礎になる技術が信号処理です。
そして信号処理で扱うあらゆる信号には影のようにつきまとってくるものがあります。
そう、ノイズですね。
・電源ラインから入り込んでくるノイズ
・モータの振動によるノイズ
・電子回路のクロストークノイズ
原因は様々ですが通常、信号とノイズは必ずセットで扱わなければなりません。
最も有効なノイズ対策はノイズ源そのものを除去することですが、例えば工場での重量計測において、計測中は周囲で動いてる装置を全部止めて振動を無くしましょう!なんて現実的ではありません。
そこで活躍するのがフィルタ技術、とりわけデジタル(ディジタル)フィルタです。
このシリーズではフィルタ設計法習得に向け、フィルタ設計と信号処理の基礎に関する直感的な理解を目標に解説していきたいと思います。
なるべく数式を排して取っつきやすい説明を行っていくつもりなので、やや不自然な言い回しや誤解を招きかねない表現があるかもしれません。
そういった箇所を見つけられた場合はすみませんが、ご指摘頂けると幸いです。
本記事はその STEP1:フィルタ特性の見方 です。
他STEPへのリンクは下記です↓
STEP:0 導入編
STEP:2 インパルス応答とフィルタ
STEP:3 周波数領域における伝達関数
STEP:4 ノイズ除去実践編
簡単なフィルタ設計&性能評価をやってみたい方は下記もどうぞ↓
FIRローパスフィルタを作ってみよう!
1. 前回のおさらい
前回の記事で、デジタルフィルタの精度と応答時間にはトレードオフの関係があることを示しました。

そしてフィルタ設計のポイントは、許容されるノイズの大きさと許容される応答時間の遅れを仕様として把握することだと述べました。
ですが、前回の記事ではフィルタが持つ精度や応答時間の表し方については詳しく触れず、ただ両者に関するトレードオフ関係を示したのみでした。
もちろん実際にフィルタ設計を行う上では、フィルタの精度その他性能を定量的に表して必要な仕様を決める必要があります。
今回はそんなフィルタの性能指標、すなわちフィルタ特性の表し方、そしてその見方について解説したいと思います。
2.振幅と位相
フィルタ特性は2つに分けることができます。すなわち、 振幅特性 と 位相特性 です。
セットで 周波数特性 と呼ばれることもあります。
これら2つの特性について解説する前に、信号の振幅 と 位相 について説明します。
・振幅 = 信号の大きさ
振幅は分かりやすいですね。↓の正弦波を元に考えてみます。
この正弦波の場合、振幅はY軸(Value)の値で最大値と最小値はそれぞれ±1.0になります。
振幅については説明不要なくらい、直感的に理解できると思います。
問題はこの次の位相ですね。
・位相 = 信号の位置
位相の単位は角度です。(deg)または(rad)で表されます。
角度なのに位置を意味するとはどういうことでしょうか?
ここで、単位円を頭に思い浮かべてみます。単位円の円周をぐるっと一周したとき、
角度はどれだけ動いたことになるでしょう?360(deg)または2π(rad)ですね。
位相を信号の位置と書いたのは、 信号が円周上のどの位置にいるか、すなわち原点からどれだけ動いたか、を位相と呼んでいる という意味です。
振幅と同じように正弦波で考えてみましょう。今回は位相の違う2種類の信号を見てみます。
単位円上を動く点と正弦波を並べて動かしてみると、↓のようになります。
この場合単位円上では赤い方の点は青い方の点より先の位置にいます。(単位円上は反時計回りがプラスです)
また、正弦波の方では赤い方の線は青い方の線より先にY軸の値が小さくなっています。
これは意外と勘違いするところだと思うんですが、時間軸上で見た信号がある信号より
「進んでいる」 というのは、比較している信号より先に変化が起きているという意味になるので、形の上では進んでいる信号は比較している信号を左にシフトした形になります。
よって同時刻で見た時、赤い方 = sin(ωt+φ)は 青い方 = sin(ωt)よりφだけ位相が進んでいる、ということが確認できますね。
また、これらの図から正弦波は 「単位円を動く点のY座標を、時間が経つに従ってX軸方向にずらしながらプロットしたもの」 ということがわかります。
繰り返しになりますが、これを踏まえると位相とは、 「ある時刻での単位円上の点がどこにいるか、その位置を表す角度」 と言い換えることができます。
3.フィルタ特性
前節で、信号は振幅と位相という2つのパラメータを持っていると述べました。
これら2つのパラメータは信号の特徴そのものですが、フィルタとはその大事な振幅と位相を都合良く変化させる装置といえます。
それでは続いてフィルタの振幅特性と位相特性について見ていきましょう。
とりあえず、適当なフィルタの振幅特性と位相特性の図を並べてみます。
前節の最初で振幅特性と位相特性をセットにして周波数特性と呼ばれることがある、と書いた通り、どちらの図でも横軸は周波数(Hz)です。
つまり、フィルタ特性はフィルタへの入力信号に対して出力信号がどうなるかを周波数ごとに定義したもの、ということですね。
振幅特性であれば振幅がどう大きくなったり小さくなったりするか、位相特性であれば位相がどう進んだり遅れたりするかを定義しています。
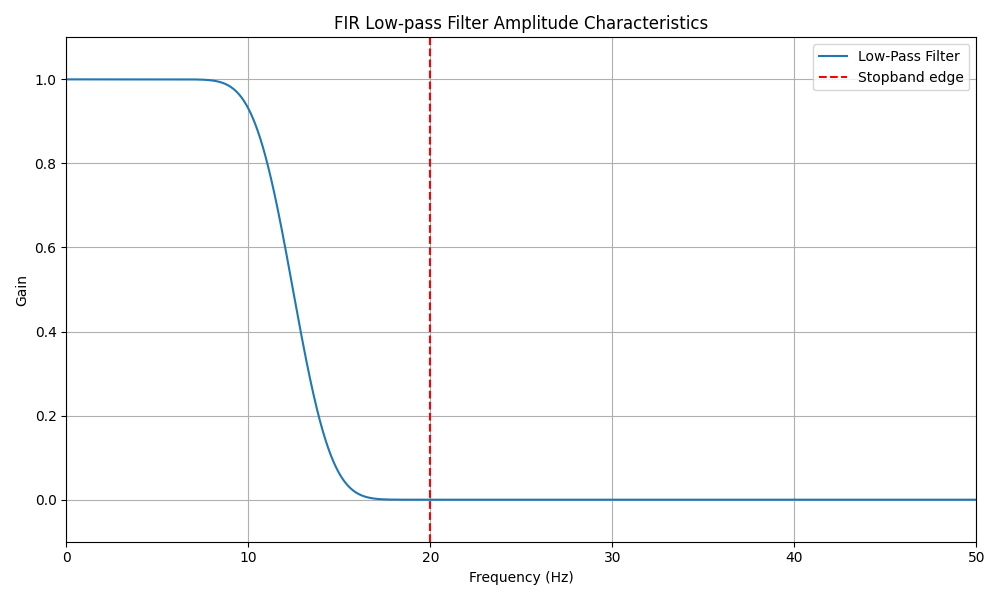
今回の場合、振幅特性と位相特性はそれぞれ下記のようになっています。
<振幅特性>
8Hzぐらいから振幅が下がり始め、20Hz以上でゲインが0、すなわち振幅が0になります。
なのでこのフィルタは振幅特性で見ると ローパスフィルタ のはたらきをします。
<位相特性>
先程の図では位相特性はなんだかギザギザでよく分からないですね。ですが、↓赤枠内の青丸に注目してみてください。-180degから+180degにジャンプしていますよね。
ここでまた単位円を想像してみてほしいんですが、単位円上で-180degと+180degは同じ
位置ですよね?なので、これは180degの符号が反転した結果、グラフ上ではジャンプして
いるように見えている、ということです。
先程の図と全く同じ位相特性を、ジャンプ無しで描画すると↓になります。
振幅特性では20Hz以上は振幅0になるため、ここでも20Hzを境に位相特性が大きく変わっています。しかし、20Hz以上はどうせ消えてしまう信号のため、どんな位相になろうがどうでも良いですよね。
結局大事なのは20Hzまでの位相特性で、それはこのフィルタでは図の通り完全に直線になっています。
このような、周波数と位相変化の関係が完全に直線になる位相特性のことを 線形位相特性 と呼びます。
例えばある線形位相特性のフィルタに10Hzの信号を入力した場合に位相が45deg進んで出力されるとしたら、その倍で20Hzの信号を入力すると、位相も倍の90deg進んで出力される、という性質を持つということです。
※余談ですが、位相特性がジャンプして描かれている場合は「ラップ」、ジャンプせずにつなげて描かれている場合は「アンラップ」されているという呼び方をします。
ここまでまとめると、この節で示したフィルタは下記の性質を持っています。
・振幅特性:20Hz以上が阻止帯域のローパス特性
・位相特性:線形位相特性
それでは、テスト用の信号をフィルタに入力した場合の出力がどうなるか見てみましょう。
4.フィルタの入出力確認
入力信号として周波数の異なる正弦波を複数作成し、ひとつずつフィルタに入力します。
それに対するフィルタの出力信号の振幅と位相をチェックして、前節で見た周波数特性通りになっているかを確認していこうと思います。
(1). 3.75Hzの正弦波
予想:振幅変化なし、位相は+180deg
結果:予想通り振幅変化なし、位相は+方向に180degずれる
(2). 5.625Hzの正弦波 -> (1)3.75Hzの1.5倍の周波数
予想:振幅変化なし、位相は+270deg ※(1)の位相変化なので180*1.5 = +270deg
結果:予想通り振幅変化なし、
位相は-方向に90degずれる、つまり+方向に270degずれているため予想通り
(3). 20Hzの正弦波
予想:振幅は0、位相は変化なし
結果:予想通り振幅はほぼ0、位相は変化なし(青い丸と赤い丸が重なっている)
(4). 24.375Hzの正弦波
予想:振幅は0、位相は+90deg
結果:予想通り振幅はほぼ0、位相は+方向に90degずれる
※すみません、サンプリングの都合上ちょっと元の波形が歪んでます
まとめ
さて、前節で(1)~(4)まで4種類の正弦波をフィルタに入力し、出力信号を見てきましたが、どれもフィルタの周波数特性通りの信号になってくれているようです。
したがって所望の周波数特性を持つフィルタを設計できれば、その通りに入力信号の振幅と位相を変化させて望み通りの出力信号としてくれるはずです。
と、ここまででフィルタ特性の意味と見方についての説明は終わりですが、おや?と思われた方もおられるのではないでしょうか?
元々STEP0においてトレードオフと述べていたのは、フィルタの 精度と応答時間 についてだったはずです。しかし、本記事において出てきたフィルタ特性は 振幅と位相 で、精度は振幅に関係するだろうと予想できますが、応答時間は直接登場していません。
次回記事ではその疑問に答えるため、さらにはフィルタを設計するために必要となる複数の重要な概念について述べようと思います。