【scikit-learn】Pythonで線形回帰 #Python

はじめに

scikit-learnを用いた線形回帰の実装方法について解説いたします。線形回帰の理論ついてはこちらにまとめましたので、理論を学びたい方は参考にして下さい。この投稿を読めば以下のことが分かります。

Pythonで線形回帰を実行する方法
偏回帰係数（Estimated coefficients）の意味と算出方法
切片（intersept）の算出方法
決定係数（R²）の算出方法

※機械学習やプログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。

Pythonでの実装

環境

conda 4.8.3
python 3.8.3
pandas 1.0.5
matplotlib 3.2.2
numpy 1.18.5
scikit-learn 0.23.1

データの前処理

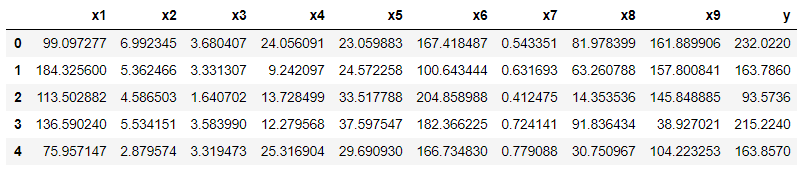
線形回帰するデータを読み込んでいきます。データはGitHubに保存しているdf.csvのデータを用います。このデータはこちらの投稿にて欠損値の除去などの前処理を行ったデータです。

import pandas as pd
df = pd.read_csv("df.csv", encoding="shift_jis")
df.head()

読み込んだデータの大きさを確認しておきます。

df.shape

出力結果

(707, 10)

次に読み込んだデータを正規化しておきます。今回のデータであればx1は100程度の大きさですが、x7は1以下とかなり大きさが違うことが分かります。特に変数間で大きさ（オーダー）が異なる場合、そのままの数字を使うと影響度が上手く評価できなかったり、モデルの精度が下がったりする恐れがあります。詳しくはこちらにまとめていますので、参考にして下さい。

# ライブラリーのインポート
from sklearn.preprocessing import StandardScaler

# 標準化の処理の実行（説明変数に対してのみ実行）
sc = StandardScaler()
sc.fit(df.iloc[:, :-1])
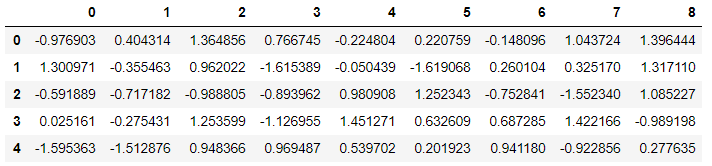
sc_df = pd.DataFrame(sc.transform(df.iloc[:, :-1]))
sc_df.head()

目的変数のデータ列を追加して、データの行ラベルを修正しておきます。（0～8となっているので、元データのようにx1～ラベルをつけます）

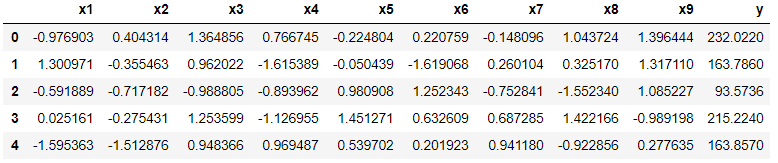
sc_df["y"] = df["y"]
sc_df.columns = df.columns
sc_df.head()

データを訓練データとテストデータに分割していきます。今回は「訓練データ7割：テストデータ3割」とします。

#データの分割
from sklearn.model_selection import train_test_split

sc_X = sc_df.iloc[:, :-1].values
sc_y = sc_df.iloc[:, -1].values
#再現性や後の検討を考えてrandom_stateは指定しておくことがおすすめ 
sc_X_train, sc_X_test, sc_y_train, sc_y_test = train_test_split(sc_X, sc_y, test_size=0.3, random_state=1)

#データの分割を確認
print("分割後のデータ")
print(sc_X.shape)
print(sc_X_train.shape)
print(sc_X_test.shape)

出力結果

分割後のデータ
(707, 9)
(494, 9)
(213, 9)

線形回帰の実行

sklearn.linear_modelのLinearRegressionクラスで線形回帰を実行していきます。詳しい使い方は公式ドキュメントを参照するのがよいと思います。

from sklearn.linear_model import LinearRegression

reg_lr = LinearRegression()
# 訓練データにモデルを適用する
reg_lr.fit(sc_X_train,sc_y_train)

出力結果

LinearRegression()

LinearRegression()の重要なパラメータは"fit_intercept"で切片(intercept)を求めるか否かを選択します。 defaultは"True"（=切片を求める）ですが、"False"にすると切片は計算されずに0になります。

偏回帰係数と切片の算出

どのような線形回帰モデルができたのか確認していきます。（この段階で結果の可視化をしてもよいかもしれませんね）

# 重み（偏回帰係数）を計算
reg_lr.coef_
# 重みをデータフレームとして表示
coef = reg_lr.coef_
df_coef = pd.DataFrame(coef).T
df_coef.columns = df.columns[:-1]
df_coef.index = ["Estimated coefficients"]
df_coef = df_coef.round(2)
df_coef

切片を計算します。

reg_lr.intercept_

出力結果

176.2138417291392

線形回帰モデルは以下の式であることが分かります。
y = (-35.7)x1 + (-4.11)x2 + (-9.41)x3 + (-9.35)x4 + (-9.03)x5 + (-3.24)x6 + (2.31)x7 + (56.26)x8 + (-3.09)x9 + 176.21

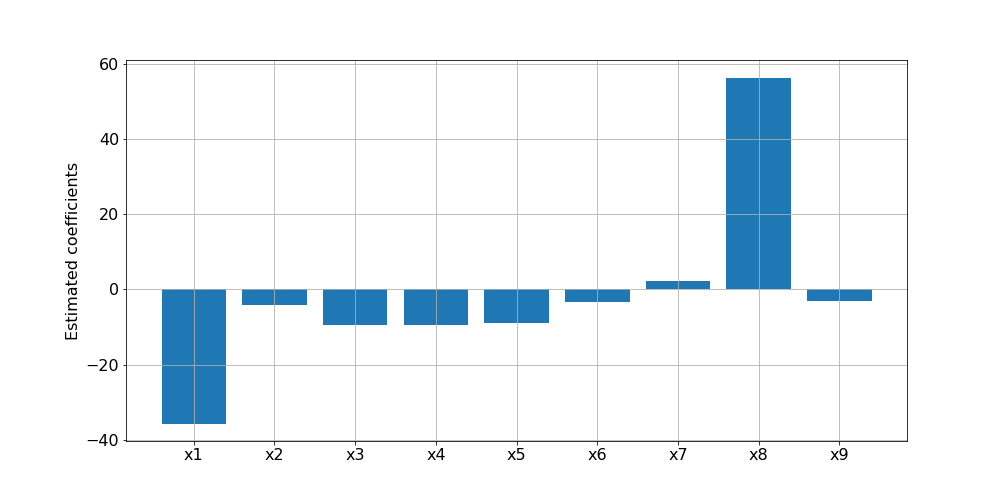
偏回帰係数をグラフ化してみます。

import matplotlib.pyplot as plt
import numpy as np

# パラメータ数を定義しておく
num = len(df_coef.columns)
# グラフの大きさを設定
plt.figure(figsize=(14, 7))
# 文字の大きさを設定
plt.rcParams["font.size"] = 16
# 棒グラフの設定plt.bar(x,height)
plt.bar(df_coef.columns, coef)
#plt.xtickes(分割数,割り当てるラベル)
plt.xticks(np.arange(num),df_coef.columns)
plt.ylabel("Estimated coefficients")
plt.grid()
plt.show()

この結果から、因子としてx1とx8の影響度が大きいことが分かります。また、x8の値が大きくなればyの値は大きく予測される一方で、x1の値が大きくなればyの値は小さく予測されるということも読み取れます。

決定係数の算出

決定係数R²を求めます。

reg_lr.score(sc_X_test,sc_y_test)
print('{:.3f}'.format(reg_lr.score(sc_X_test,sc_y_test)))

出力結果

0.909

それなりに高い精度で予測が行われていることが分かります。MSEとRMSEも算出しておきます。（このあたりの用語はまた勉強してまとめたいと思います）

train_pred = reg_lr.predict(sc_X_train)
train_mse = mean_squared_error(y_true=sc_y_train , y_pred=train_pred)
print("訓練データのMSE：" + '{:.1f}'.format(train_mse))
print("訓練データのRMSE：" + '{:.1f}'.format(np.sqrt(train_mse)))
test_pred = reg_lr.predict(sc_X_test)
test_mse = mean_squared_error(y_true=sc_y_test , y_pred=test_pred)
print("テストデータのMSE：" + '{:.1f}'.format(test_mse))
print("テストデータのRMSE：" + '{:.1f}'.format(np.sqrt(test_mse)))

出力結果

訓練データのMSE：583.9
訓練データのRMSE：24.2
テストデータのMSE：424.0
テストデータのRMSE：20.6

予測結果の可視化

予測結果をグラフ化していきます。

x = np.linspace(0, 450, 900)

plt.rcParams["font.size"] = 14
plt.scatter(x=sc_y_train, y=train_pred, s=15, label='train_data', color="b")
plt.scatter(x=sc_y_test, y=test_pred, s=15, label='test_data',color="r")
plt.plot(x, x, color="gray", linestyle="--")
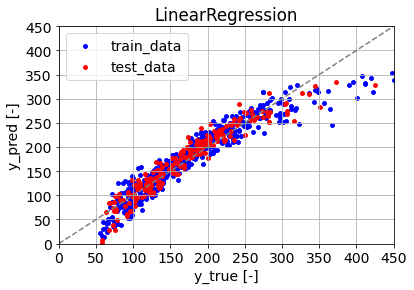
plt.title("LinearRegression")
plt.xlabel("y_true [-]")
plt.ylabel("y_pred [-]")
plt.xlim(0, 450)
plt.ylim(0, 450)
plt.xticks(np.arange(0,500,50))
plt.yticks(np.arange(0,500,50))
plt.grid()
plt.legend()
plt.show()

plt.savefigでグラフを保存したのですが下部が微妙に切れてしまいました。こちらを参考にして、そのような際はbbox_inches='tight'としてplt.savefig("LinearRegression.png", bbox_inches='tight')とすれば上手く保存できました。

訓練データを青色、テストデータを赤色で示しています。全体的にある程度予測できていますが、yが小さい領域（100以下）と大きい領域（300以上）で予測と実測の乖離が大きいことが読み取れます。

モデルの改良の検討

yが大きい領域で特に予測の精度が低いことが読み取れたので、yが250以上のデータで新たに予測モデルを組んでみます。まず、yが250以上のデータを抜き出します。

sc_high_df = sc_df[sc_df["y"]>=250]
sc_high_df.shape

出力結果

(104, 10)

この104個のデータに対して同様に線形回帰モデルを作っていきます。

#ホールドアウト法で訓練データとテストデータを分割、訓練データ7割：テストデータ3割とする
#標準化後のデータに対して実行、sc_yについてはyと同じもの
sc_high_X = sc_high_df.iloc[:, :-1].values
sc_high_y = sc_high_df.iloc[:, -1].values
sc_high_X_train, sc_high_X_test, sc_high_y_train, sc_high_y_test = train_test_split(sc_high_X, sc_high_y, test_size=0.3, random_state=1)

#データの分割を確認
print("分割後のデータ")
print(sc_high_X.shape)
print(sc_high_X_train.shape)
print(sc_high_X_test.shape)

出力結果

(104, 9)
(72, 9)
(32, 9)

作成した線形回帰モデルの偏回帰係数について、①すべてのデータで予測したモデル、②yが250以上のデータのみで予測したモデルで比較してみます。

reg_lr.fit(sc_high_X_train, sc_high_y_train)
#重みの算出し、Dataframeに格納して表示
reg_lr.coef_
high_coef = reg_lr.coef_
df_high_coef = pd.DataFrame(high_coef).T
df_high_coef.columns = df.columns[:-1]
df_high_coef.index = ["Estimated coefficients"]
df_high_coef = df_high_coef.round(2)
#全データでの分析と併せて重みを一覧で表示
df_coef_datas = df_coef.append(df_high_coef)
df_coef_datas.index = ["all_data", "over_250"]
df_coef_datas

この結果をグラフ化してみます。

#縦軸のデータの読み込み 
height1 = coef
height2 = high_coef
#横軸の指定に使用
num = len(df_coef.columns)
left = np.arange(num)
labels = tuple(df_coef.columns)
#グラフの大きさを設定
plt.figure(figsize=(15, 9))
#棒グラフ間の距離の指定に使用
width = 0.3
#plt.bar(x,height,width=0.8)
plt.bar(left, height1, color='b', width=width, align='center',label='all_data')
plt.bar(left+width, height2, color='r', width=width, align='center',label='over_250')
#plt.xtickes(分割数,割り当てるラベル)
plt.xticks(left + width/2, labels)
plt.ylabel("Estimated coefficients")
plt.grid()
plt.legend(fontsize=15)
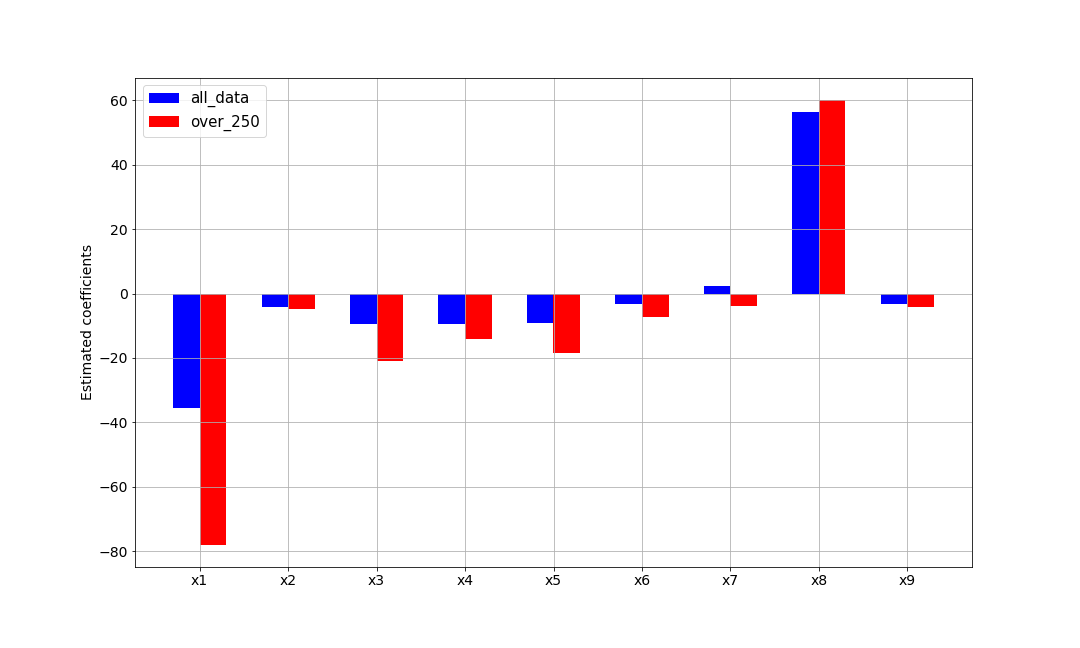
plt.show()

①すべてのデータで予測したモデルを青色、②yが250以上のデータのみで予測したモデルを赤色で示していますが、②のデータではx1の絶対値が大きくなっていることが分かります。

決定係数を算出します。

reg_lr.score(sc_high_X_test,sc_high_y_test)
print("{:.3f}".format(reg_lr.score(sc_high_X_test,sc_high_y_test)))

出力結果

0.783

全データを用いて予測したときに比べてR²は悪化しています。この原因としては、精度高く予測できている領域（yが100～250）のデータが減ったことではないかと推測します。

予測結果をグラフ化します。

x = np.linspace(0, 450, 900)
plt.rcParams["font.size"] = 14
plt.scatter(x=sc_high_y_train, y=high_train_pred, s=15, label='train_data', color="b")
plt.scatter(x=sc_high_y_test, y=high_test_pred, s=15, label='test_data',color="r")
plt.plot(x, x, color="gray", linestyle="--")
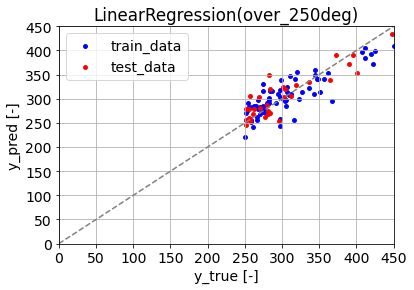
plt.title("LinearRegression(over_250deg)")
plt.xlabel("y_true [-]")
plt.ylabel("y_pred [-]")
plt.xlim(0, 450)
plt.ylim(0, 450)
plt.xticks(np.arange(0,500,50))
plt.yticks(np.arange(0,500,50))
plt.grid()
plt.legend()
plt.show()

視覚的には、全データを用いて予測したときに比べて、yが250以上の領域でも予測と実測の乖離が小さいように見えます。

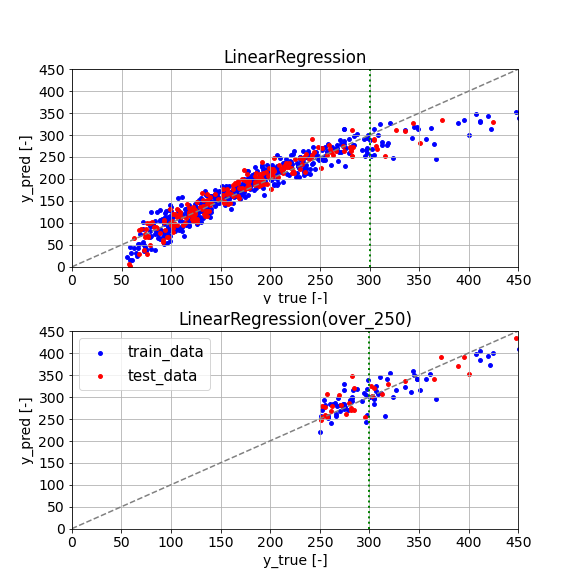
以下で、①すべてのデータで予測したモデル、②yが250以上のデータのみで予測したモデルの予測結果を並べて表示してみます。

x = np.linspace(0, 450, 900)
x_300 = np.linspace(300, 300, 900)

plt.figure(figsize=(8, 8))
plt.subplot(2,1,1)
plt.scatter(x=sc_y_train, y=train_pred, s=15, label='train_data', color="b")
plt.scatter(x=sc_y_test, y=test_pred, s=15, label='test_data',color="r")
plt.plot(x, x, color="gray", linestyle="--")
plt.plot(x_300, x, color="green", linestyle=":", linewidth = 2.0)
plt.title("LinearRegression")
plt.xlabel("y_true [-]")
plt.ylabel("y_pred [-]")
plt.xlim(0, 450)
plt.ylim(0, 450)
plt.xticks(np.arange(0,500,50))
plt.yticks(np.arange(0,500,50))
plt.grid()
plt.legend(fontsize=15)

plt.figure(figsize=(8, 8))
plt.subplot(2,1,2)
plt.scatter(x=sc_high_y_train, y=high_train_pred, s=15, label='train_data', color="b")
plt.scatter(x=sc_high_y_test, y=high_test_pred, s=15, label='test_data',color="r")
plt.plot(x, x, color="gray", linestyle="--")
plt.plot(x_300, x, color="green", linestyle=":", linewidth = 2.0)
plt.title("LinearRegression(over_250)")
plt.xlabel("y_true [-]")
plt.ylabel("y_pred [-]")
plt.xlim(0, 450)
plt.ylim(0, 450)
plt.xticks(np.arange(0,500,50))
plt.yticks(np.arange(0,500,50))
plt.grid()
plt.legend(fontsize=15)
plt.show()

この結果を見ると、yが300以下の予測の際は①すべてのデータで予測したモデルを活用し、yが300より大きい予測の際は②yが250以上のデータのみで予測したモデルを活用することで全体としての精度が上がるのではないかと考えられます。（余談ですが、matplotを最近少し勉強しているのでが、このグラフの可視化方法はあまり良くない気がしています…また勉強します）

まとめ

scikit-learnを用いた線形回帰の実装方法について、以下の項目を中心に解説いたしました。

Pythonで線形回帰を実行する方法
偏回帰係数（Estimated coefficients）の意味と算出方法
切片（intersept）の算出方法
決定係数（R²）の算出方法