はじめに
特徴量スケーリングの手法である**「標準化」と「正規化」について、原理や使い分けなどを解説いたします**。
※プログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。
標準化と正規化
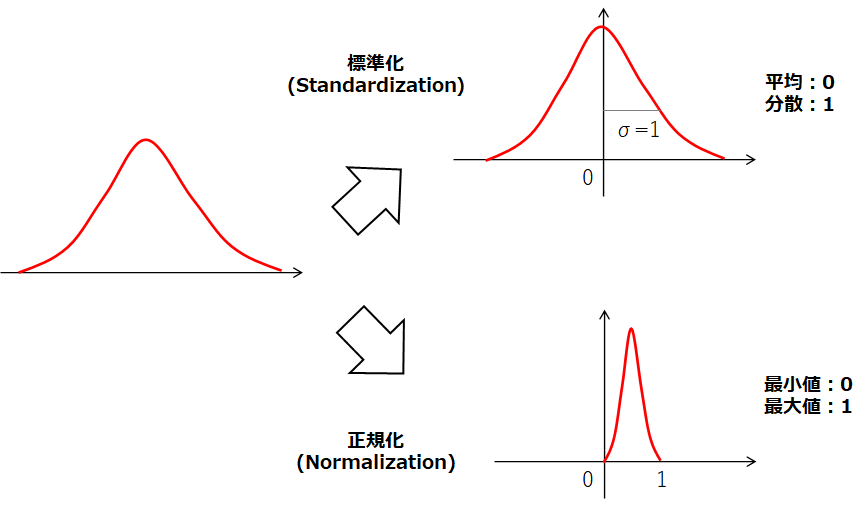
- 標準化(Standardization)は「平均を0、分散を1とするスケーリング手法」
- 正規化(Normalization)は「最小値を0、最大値を1とするスケーリング手法」
ただ、分野によっては標準化や正規化の定義も異なるようなので上記の内容がいつでもどこでも正しいというわけではないので注意が必要です。ややこしいですね…そのあたりに関しては、こちらやこちらを参照ください。
図で表すと以下のようなイメージです。(こんなにきれいに分布しているデータはないですが…)
標準化
「平均を0、分散を1」にするので、あるデータXは以下のように標準化されます。ただし、X全体の平均をμ、標準偏差をσとします。
\frac{X-μ}{σ}
ちなみに(標準偏差)2が分散なので、分散が1のとき標準偏差も1となります。こちらを参照すると、pythonのライブラリによって分散の定義が異なる(標本分散or不偏分散)ようなのでその点は注意が必要です。なお、標本分散は各データと平均との差の二乗和をnで割るのに対して、不偏分散はn-1で割ります。
正規化
「最小値を0、最大値を1」のするので、(それ以外の正規化もあるようです)あるデータXは以下のように正規化されます。ただし、X全体の最大値をXmax、最小値をXminとします。
\frac{X-X_{min}}{X_{max}-X_{min}}
標準化と正規化の使い分け
標準化を用いる場合
- 最大値及び最小値が決まっていない場合
- 外れ値が存在する場合(外れ値が存在するデータに対して正規化を行うとスケーリングが外れ値に大きく影響されてしまいます)
- 機械学習で回帰モデルを構築する際は一般的に用いられる
正規化を用いる場合
- 最大値及び最小値が決まっている場合
- 画像処理におけるRGBの強さを扱う場合(学習コストを下げる事ができるため)
そもそもなぜ特徴量スケーリングをするのか?
例えば線形回帰では、各説明変数の値に基づいて重みづけを行います。**各説明変数間で値が大きく異なる場合、重みづけが不均衡に働き、影響度が上手く評価できなかったりモデルの精度が下がったりする恐れがあります。**そのような悪影響を回避するために「標準化」と「正規化」といったスケーリングを行います。こちらのサイトには例を示して説明がされていました。**ただ、決定木やランダムフォレストなどのtree系の回帰や分類は特徴量のスケーリングは不要とされています。**その理由としては、それらの手法は各説明変数の値の大小を分岐条件としているのでスケールに依存しないからです。
まとめ
特徴量スケーリングの手法である「標準化」と「正規化」について、原理や使い分けなどを解説いたしました。
- 標準化(Standardization)は「平均を0、分散を1とするスケーリング手法」
- 正規化(Normalization)は「最小値を0、最大値を1とするスケーリング手法」