Feature Scalingとは
特徴量の取りうる値の範囲(スケール)を変えることです。
データセットの特徴量間でスケールが異なることは多々あります。例えば、体重と身長、家の価格と部屋数では、その単位と値の範囲が異なります。
そのような特徴量間で異なるスケールのデータセットをモデルで学習させた場合、うまく学習できないということがおこるのです。
そのため、学習前の前処理で、特徴量間のスケールを揃える必要があります。
Feature Scalingの種類
主なFeature Scalingの種類として、以下の2つがあります。
- 正規化(normalization)
- 標準化(standardization)
正規化(normalization)とは
正規化とは、特徴量の値の範囲を一定の範囲におさめる変換になります。主に[0, 1]か、[-1, 1]の範囲内におさめることが多いです。
例えば、[0, 1]におさめるとすると、特徴量$x$の$i$番目の値の変換の式は以下になります。
$x_{norm, i} = \frac{x_i-x_{min}}{x_{max}-x_{min}} $
$x_{norm}$が正規化された$x$になります。
$x_{min}$は$x$の最小値、 $x_{max}$は$x$の最大値です。
これを計算することで、正規化する前の特徴量の最小値は正規化されて0に、最大値は1となり、新しい特徴量は[0,1]におさまります。
標準化(standardization)とは
標準化とは、特徴量の平均を0、分散を1にする変換になります。変換の式は以下になります。
$x_{std} = \frac{x-m_{x}}{s_{x}}$
$x_{std}$が標準化された$x$になります。
$m_{x}$が$x$の標本平均、 $s_{x}$が$x$の標本標準偏差になります。標準化した後に平均が0になっていることは値を見ればすぐにわかります。
分散が1になることは実際に計算して確かめてもいいですが、直感的に理解してみましょう。
本来、標準偏差は、データのちらばり=各データが平均からどれくらい離れているか、を表していました。
ですので、標準偏差で、データ全体を割るということは散らばりを1にするということだとわかります。
分散を求める公式は、
${\frac {1}{n}}\sum_{{n=1}}^{n}(x-m_{x})^{2}$
になります。標準偏差$x_{std}$は分散の平方根の値になります。
なぜ、Feature Scalingをするのか
まず、勾配降下法などの距離を用いて学習させるモデルの場合を考えます。
特徴量間でスケールが揃っていないデータセットで学習させる場合を考え、どのような問題が生じるか考えます。
今、学習させるモデルを2つの特徴量$x,y$をもつ線形モデル$f(x,y)$を考えます。
特徴量$x,y$にかかるパラメータを、各々 $w_x,w_y$とします。
コスト関数$E(\boldsymbol w)$は平均二乗誤差(Mean Squared Error)と定義し、基底関数は恒等関数とします。
すると、勾配降下法でのパラメータの更新幅は、
\Delta \boldsymbol w = (\Delta w_x, \Delta w_y)
= - \eta \left(\frac{\partial E(\boldsymbol w)}{\partial w_x}, \frac{\partial E(\boldsymbol w)}{\partial w_y} \right)\\
= - \eta \left( \sum_{i}^N \{f(x_i,y_i)-t_i\}x_i, \sum_{i}^N \{f(x_i,y_i)-t_i\}y_i \right) \\
= - \eta \sum_{i}^N \{f(x_i,y_i)-t_i\} \left( x_i, y_i \right)
tは正解ラベルです。$\Delta w_x$は$x$の大きさに、$\Delta w_y$は$y$の大きさにそれぞれ依存していることがわかります。
もし、$x$のスケールが大きく、反対に$y$のスケールが小さい場合は、 $w_y$の更新幅は小さく、学習が$w_x$に比べて遅くなってしまいます。その結果、パラメータ間で更新幅に偏りが生じます。
そこで、特徴量にFeature scalingを行うことによって、最適な解決法を見つけるまでのステップがすくなくなるというメリットがあります。
一方、分類問題おいても同様に、データの特徴量にスケーリングを施し、学習を行えば、スケーリングを行わない場合よりも分類の精度がよくなる結果をもらたします。
以下で実例をあげて説明します。
正規化と標準化の使い分け
基本は標準化を用います。理由は、正規化の場合、外れ値が大きく影響してしまうためです。
ただし、画像データの場合は学習コストを下げるため、[0,1]の範囲に収まるよう255.0で割ることで正規化するのが一般的です。
正規化
使うとき:
- 画像処理におけるRGBの強さ[0,255]
- sigmoid, tanhなどの活性化関数を用いる、NNのいくつかのモデル
標準化
使うとき:
- ロジスティック回帰、SVM、NNなど勾配法を用いたモデル
- kNN, k-meansなどの距離を用いるモデル
- PCA, LDA(潜在的ディリクレ配分法), kernel PCA などのfeature extractionの手法
使わないとき:
決定木、ランダムフォレスト
irisデータで標準化、正規化の効果を確認
sklearnでの実装
irisのデータを用いて標準化、正規化の効果を確認します。
irisは4つの説明変数と、1つの目的変数(アヤメの品種)からなります。そのうち、'petal length'、'petal width'の2説明変数を用いて、品種を予測する分類問題を、ロジスティック回帰で行います。
元のデータと、標準化したデータとで、学習結果に違いがどう出るか確認してみましょう。
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
# datasetの読み込み
iris = load_iris()
data = np.concatenate((iris.data, iris.target.reshape(-1,1)), axis=1)
df = pd.DataFrame(data)
cols = iris.feature_names
cols.append('type')
df.columns = cols
df.head()

特徴量を2つ選択し、その2つによってどう分類ができそうかを、labelとともにデータをplotすることで確認しましょう。
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
x1 = iris.data[:,2].reshape(-1,1)
x2 = iris.data[:,3].reshape(-1,1)
# 目的変数を作成
y = iris.target
# 配列を軸指定して結合する
x=np.concatenate((x1,x2), axis=1)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=3)
plt.scatter(x1[y==0],x2[y==0],marker="x")
plt.scatter(x1[y==1],x2[y==1],marker="x")
plt.scatter(x1[y==2],x2[y==2],marker="x")
pl.grid()
plt.show()

横軸がx1, 縦軸がx2, 色が正解ラベルの品種を表します。
sklearnライブラリの、
正規化: preprocessing.MinMaxScaler
標準化: preprocessing.StandardScaler
を用いて、簡単に正規化、標準化を行うことができます。
# 正規化
from sklearn.preprocessing import MinMaxScaler
mmsc = MinMaxScaler()
# 訓練用のデータを正規化する
x_train_norm = mmsc.fit_transform(x_train)
# 訓練用データを基準にテストデータも正規化
x_test_norm = mmsc.transform(x_test)
print(x_train_norm.max()) #1.0
print(x_train_norm.min()) #0.0
# test用はtrainを基準に標準化してるので、多少0,1からずれる
print(x_test_norm.max()) #1.0357142857142858
print(x_test_norm.min()) #-0.017857142857142877
# 標準化
from sklearn.preprocessing import StandardScaler
stdsc = StandardScaler()
# 注意
# 訓練用のデータを標準化
x_train_std = stdsc.fit_transform(x_train)
# 訓練用データを基準にテストデータも標準化
x_test_std = stdsc.transform(x_test)
print(x_train_std.mean()) # 1.9032394707859825e-16
print(x_train_std.std()) #1.0
# test用はtrainを基準に標準化してるので、多少0,1からずれる
print(x_test_std.mean()) #-0.11061956642887648
print(x_test_std.std()) #1.0400750810723733
plotの変化を確認する
変換前と変換後のデータをplotしてみて、幾何的にどう変化させているのか確認しましょう。
plt.axis('equal')
plt.scatter(x[:,0],x[:,1], marker="x", label="org")
x_norm = mmsc.transform(x)
x_std = stdsc.transform(x)
plt.scatter(x_std[:,0],x_std[:,1], c='red',marker="x", label="std")
plt.scatter(x_norm[:,0],x_norm[:,1], c='green',marker="x", label="norm")
plt.legend()
plt.grid()
plt.show()

- 青: 元データ
- 赤: 標準化
- 緑: 正規化
です。青の元データは横軸x1の方の分散が大きいです。また、緑の正規化されたデータは[0,1]内におさまっています。
ただ、訓練データを用いているため、いくつかその範囲を超えているtestデータも確認できます。
標準化による学習結果の違い
logistic回帰を用いてfittingします。
logistic回帰では標準化を使うので、標準化と元のデータのみで学習結果の違いを比べます。
つまり上の図の緑と青のデータで学習させるということです。
from sklearn.linear_model import LogisticRegression
from matplotlib.colors import ListedColormap
lr=LogisticRegression()
lr_std = LogisticRegression()
lr.fit(X_train,y_train)
print('元データのスコア :',lr.score(X_train,y_train)) #元データのモデルの予測精度(約86.7%)
lr_std.fit(X_train_std,y_train)
print('標準化したデータのスコア :',lr_std.score(X_train_std,y_train)) #標準化したデータのモデルの予測精度(約94.3%)
結果は以下の通りになります。
元データのスコア : 0.8666666666666667
標準化したデータのスコア : 0.9428571428571428
データを標準化した場合の方が、精度が上がっていることがわかります。
最後に、それぞれのfittingの結果の違いを確認するため、以下の決定境界をplotする関数を定義します。
def decision(X, y, model, scale):
colors = 'red,blue,lightgreen'.split(',')
cmap = ListedColormap(colors[:len(np.unique(y))])
x1_min, x1_max = X[:, 0].min(), X[:,0].max()
x2_min, x2_max = X[:, 1].min(), X[:,1].max()
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02*scale),
np.arange(x2_min, x2_max, 0.02*scale))
z = model.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
z = z.reshape(xx1.shape)
plt.contourf(xx1, xx2, z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y==cl, 0], y=X[y==cl, 1],
alpha=0.8, c=cmap(idx),
label=cl)
元データと標準化したデータで学習して決定境界で分類します。
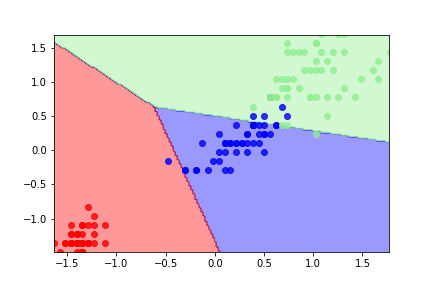
①元データで学習した結果の分類
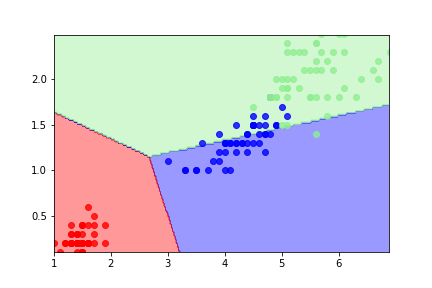
②標準化したデータで学習した結果の分類
①よりも②の方が、よく分類できていることがわかります。