Pythonで基礎から機械学習 「重回帰分析」

はじめに

　この「Pythonで基礎から機械学習」シリーズの目的や、環境構築方法、シリーズの他の記事などは以下まとめページを最初にご覧下さい。

　今回は、前回のPythonで基礎から機械学習 「単回帰分析」を読んだことが前提の内容となっております。

　また、本記事は、初学者が自分の勉強のために個人的なまとめを公開している記事になります。そのため、記事中に誤記・間違いがある可能性が大いにあります。あらかじめご了承下さい。

　より良いものにしていきたいので、もし間違いに気づいた方は、編集リクエストやコメントをいただけましたら幸いです。

　本記事のコードは、Google Colaboratory上での実行を想定しています。本記事で使用したGoogle ColabのNotebookは以下となります。

02_multiple_regression.ipynb

重回帰分析

　重回帰分析は、簡単に言うと前回学習した単回帰分析の入力変数を1つから複数（N個）に増やしたものです。それにより、単回帰から、以下のような変化があります。

• 行列を使った計算が増える（複雑になる）
• 複数の入力変数の粒度を揃えるために正規化が必要
• 単回帰と同様の計算に対して、入力変数の数に応じた補正が必要になる場合がある
• 入力変数同士の相関が強い（線形従属）の場合は、うまくモデル化できないので、正則化・次元削減といった対策が必要

　これらに注意して、実際に手を動かしながら確認していきましょう。

　前回同様、scikit-learnを使うだけでなく、Numpyを使って実際に値を導出しながら、その値が持つ意味を確認していきます。

　重回帰分析に関して、参考にしたサイトは以下です。書籍に関しては、冒頭のまとめページを参照下さい。

7. 単回帰分析と重回帰分析(Chainer Tutorial)

　その他、コードの実装で参考にしたサイトは、本記事の最後に列挙します。

データの読み込みと可視化

　単回帰のときと同様、データの読み込みと可視化を行います。

　今回は、前回の最後で紹介したUC バークレー大学の UCI Machine Leaning Repository にて公開されている、「Wine Quality Data Set (ワインの品質)」の赤ワインのデータセットを利用します。
まずは、以下コマンドで、今回解析する対象となるデータをダウンロードします。

!wget http://pythondatascience.plavox.info/wp-content/uploads/2016/07/winequality-red.csv

　次に、pandasで分析するcsvファイルを読み込み、ファイルの中身の冒頭部分を確認します。

　pandas, matplotlibなどのライブラリの使い方に関しては、以下ブログ記事を参照下さい。
Python/pandas/matplotlibを使ってcsvファイルを読み込んで素敵なグラフを描く方法（Mac/Raspberry Pi）

import pandas as pd

df = pd.read_csv('winequality-red.csv', sep=';')
df.head()

　xに説明変数全体、x1に説明変数として密度(density)、x2に説明変数として揮発酸（volatile acidity）、yに目的変数としてアルコール度数(alcohol)を入力します。

x = df[['density', 'volatile acidity']]
y = df[['alcohol']]
x1 = df[['density']]
x2 = df[['volatile acidity']]

print(x.shape)
print(y.shape)

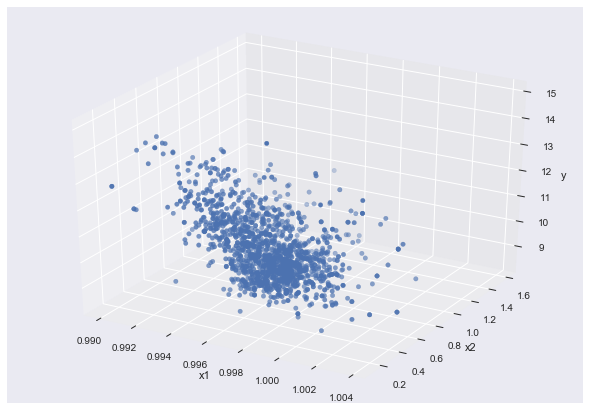
まずは、x1, x2, yをグラフで可視化します。matplotlibというライブラリを使います。

from mpl_toolkits.mplot3d import Axes3D  #3Dplot
import matplotlib.pyplot as plt
import seaborn as sns

fig=plt.figure()
ax=Axes3D(fig)
 
ax.scatter3D(x1, x2, y)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
 
plt.show()

　パラメータがx1,x2,yと3つあるので、3次元プロットして可視化しています。

　重回帰の場合、更にパラメータの次元数が増える場合があります。その場合は、3次元にプロットすることは困難になります。

　ここでは紹介しませんが、3次元以上のパラメータを可視化するとき、テクニックとしては、主成分分析を行って次元数を圧縮して可視化するなどの方法があります。

正規化

　重回帰分析で、入力変数が複数になったことで重要なこととして、正規化の必要性が挙げられます。

　何故正規化が必要かというと、入力変数の単位（m, mm）や比べる対象（温度、密度）が異なり、そのままの数字を使うと、影響度合いをうまく評価できないからです。1mの変化と1mmの変化を同じ尺度で考えてはいけないのは、直感的にも分かりますよね。

　これらの変数ごとの粒度を揃えるためのデータに対して行われる前処理が正規化(normalization)です。正規化の代表的な手法は以下2つです。

• 標準化 (standardization)：平均、分散（標準偏差）を使ったもの（平均を0、分散を1にする）
• Min-Maxスケーリング(min-max scaling)：最小値(min)、最大値(max)を使ったもの（全体を 0〜1にする）

　分野によっては「正規化=標準化」だったと定義が異なり紛らわしいですが、データを一定のルールに基づいて変形して、利用しやすくすることは全て正規化と呼ぶのが一般的なようです。

　数式に関しては、以下サイトを参照ください。

　それぞれ説明していきます。

標準化

　平均と分散を使って、平均値が0、分散が1になるようにするのが標準化です。なお、標準偏差の二乗が分散なので、これ以降では分散=標準偏差として記載していきます、ご了承下さい。

　平均、分散（標準偏差）を使った標準化で紛らわしいのが、分散と不偏分散（不偏標準偏差）の違いです。

統計が専門の人は分散といえば不偏分散を当たり前のように使うので、結構食い違うことがあります。

不偏分散を使う理由は、統計的に扱うときに色々便利だかららしいのですが、この辺りは、私自身説明できるほど理解できていませんので、詳しい説明は以下リンク先など参照下さい（理解できるようになったら、このページにも追記します）。

• https://mathtrain.jp/huhenbunsan
• https://manareki.com/unbiased_std_v
• https://to-kei.net/basic/glossary/variance/
• http://cyclo-commuter.hatenablog.jp/entry/2019/03/13/105514

　また、更にややこしいのが、Pythonのライブラリのscikit-learn, pandas, numpy 機械学習でよく使われるR言語で、分散（標準偏差）をもとめるとき、デフォルトでの計算結果が、分散(population standard deviation)だったり不偏分散(sample standard deviation)だったりする点です。なので、初心者は値が合わずにパニックに陥ります（私はパニックでした）。

ちなみにデフォルトは以下のようです。ややこし過ぎですね。

• scikit-learn: 分散
• pandas: 不偏分散
• numpy: 分散
• R言語: 不偏分散

　ここから、具体的に計算して確認していきます。

scikit-learnのStandardScalerを使う方法

　scikit-learnのStandardScalerメソッドでは、コマンド一発でいわゆる普通の分散を用いて標準化を行います。

from sklearn import preprocessing

sscaler = preprocessing.StandardScaler()
sscaler.fit(x)
xss_sk = sscaler.transform(x) 
sscaler.fit(y)
yss_sk = sscaler.transform(y)

print(xss_sk)
print(yss_sk)

結果は以下となります。

[[ 0.55827446  0.96187667]
 [ 0.02826077  1.96744245]
 [ 0.13426351  1.29706527]
 ...

pandasを使う方法

　pandasで正規化する場合は、デフォルトのstdメソッドは不偏分散を使って求めます。確認してみましょう。scikit-learnの求める値と異なる値になることがわかります。

xss_pd = (x - x.mean()) / x.std()
yss_pd = (y - y.mean()) / y.std()

print(xss_pd.head())
print(yss_pd.head())

　結果は以下となります。先ほど求めた値と異なることが分かります。

    density  volatile acidity
0  0.558100          0.961576
1  0.028252          1.966827
2  0.134222          1.296660
3  0.664069         -1.384011
4  0.558100          0.961576

　不偏分散でなく、いわゆる普通の分散を用いたい場合は、stdメソッドのddofオプションを使います。

　pandasのstdメソッドのddofオプションのデフォルト値は不偏分散を求めるddof=1です。ddof=0を設定（いわゆる普通の）分散を使うと、scikit-learnの求める値と同じになります。確認してみます。

xss_pd = (x - x.mean()) / x.std(ddof=0)
yss_pd = (y - y.mean()) / y.std(ddof=0)

print(xss_pd.head())
print(yss_pd.head())

　結果は以下となります。scikit-learnのStandardScalerメソッドで求めた値と同じになりました。

    density  volatile acidity
0  0.558274          0.961877
1  0.028261          1.967442
2  0.134264          1.297065
3  0.664277         -1.384443
4  0.558274          0.961877

Numpyを使う方法

　続いてNumpyで計算します。Numpyでは、デフォルトは普通の分散です。scikit-learnのStandardScalerメソッドの計算値と同じになることを確認して下さい。

import numpy as np

x_np = x.apply(lambda x: (x - np.mean(x)) / np.std(x))
y_np = y.apply(lambda x: (x - np.mean(x)) / np.std(x))

print(x_np.head())
print(y_np.head())

　以下が計算結果です。

    density  volatile acidity
0  0.558274          0.961877
1  0.028261          1.967442
2  0.134264          1.297065
3  0.664277         -1.384443
4  0.558274          0.961877

　pandasと同様にddofオプションを使うと、不偏分散も求められます。Numpyの場合はddof=1とします。

x_np = x.apply(lambda x: (x - np.mean(x)) / np.std(x, ddof=1))
y_np = y.apply(lambda x: (x - np.mean(x)) / np.std(x, ddof=1))

print(x_np.head())
print(y_np.head())

　以下が計算結果です。

    density  volatile acidity
0  0.558100          0.961576
1  0.028252          1.966827
2  0.134222          1.296660
3  0.664069         -1.384011
4  0.558100          0.961576

標準化のまとめ

　分散か不偏分散かを意識して標準化を行うことが重要です。少なくとも、どちらで正規化をしているのかを把握するようにしておきましょう。そうしないと、思わぬ計算違いをしていまうことになります。

　最後に、平均、分散を使って正規化した変数の平均が0、分散が1になることを確認しましょう。分散のときは、分散か不偏分散かを意識します。

x_np.mean()

density             3.772732e-13
volatile acidity   -1.590973e-15
dtype: float64

y_np.mean()

alcohol    2.580411e-14
dtype: float64

x_np.std()

density             1.0
volatile acidity    1.0
dtype: float64

y_np.std()

alcohol    1.0
dtype: float64

　例えば、ここで不偏分散を用いて計算するところで、普通の分散を用いて計算すると、間違った答えが出てきてしまいます。以下で、分散が1にならないことを確認しましょう。

x_np.std(ddof=0)

density             0.999687
volatile acidity    0.999687
dtype: float64

y_np.std(ddof=0)

alcohol    0.999687
dtype: float64

min-maxスケーリング

　最小値と最大値を使って、最大値が1, 最小値が0になるように正規化をします。

　この計算は、それほど複雑ではないのでscikit-learnを使って計算した例と、Numpyを使って計算した例を紹介します。

mscaler = preprocessing.MinMaxScaler()
mscaler.fit(x)
xms = mscaler.transform(x)
mscaler.fit(y)
yms = mscaler.transform(y)

print(xms)
print(yms)

[[0.56754772 0.39726027]
 [0.49412628 0.52054795]
 [0.50881057 0.43835616]
 ...

x_ms = x.apply(lambda x: (x - np.min(x)) / (np.max(x) - np.min(x)))
y_ms = y.apply(lambda x: (x - np.min(x)) / (np.max(x) - np.min(x)))

print(x_ms.head())
print(y_ms.head())

    density  volatile acidity
0  0.567548          0.397260
1  0.494126          0.520548
2  0.508811          0.438356
3  0.582232          0.109589
4  0.567548          0.397260

scikit-learnを使った重回帰分析

正規化無し

まずは正規化なしで行います

from sklearn.linear_model import LinearRegression
import numpy as np

model_lr = LinearRegression()
model_lr.fit(x, y)

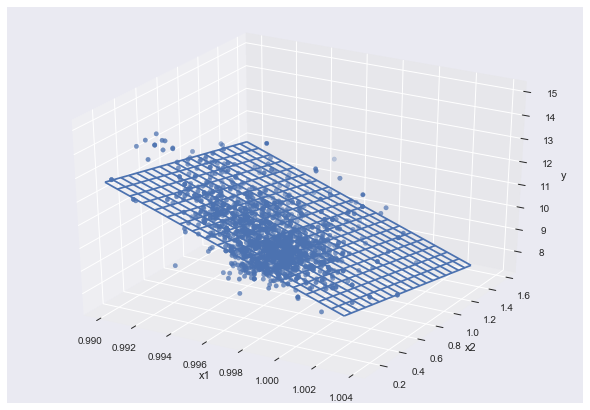
　これで完了です。一瞬ですね。早速結果を可視化します

fig=plt.figure()
ax=Axes3D(fig)

ax.scatter3D(x1, x2, y)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")

mesh_x1 = np.arange(x1.min()[0], x1.max()[0], (x1.max()[0]-x1.min()[0])/20)
mesh_x2 = np.arange(x2.min()[0], x2.max()[0], (x2.max()[0]-x2.min()[0])/20)
mesh_x1, mesh_x2 = np.meshgrid(mesh_x1, mesh_x2)
mesh_y = model_lr.coef_[0][0] * mesh_x1 + model_lr.coef_[0][1] * mesh_x2 + model_lr.intercept_[0]
ax.plot_wireframe(mesh_x1, mesh_x2, mesh_y)
plt.show()

print(model_lr.coef_)
print(model_lr.intercept_)
print(model_lr.score(x, y))

[[-277.78274856   -1.13941954]]
[287.90342428]
0.28283042699952976

　上記の数字は、それぞれ編回帰係数、切片、決定係数です。正規化をしていないため、回帰変数の値が -277.78274856と-1.13941954と差が200倍以上と非常に大きいことが分かります。

正規化（標準化）

　次は、先ほど行った標準化した値でScikit-learnを使った重回帰分析を行います。

　StandardScalerを使用して正規化したxss_sk, yss_sk を用います。

model_lr_std = LinearRegression()
model_lr_std.fit(xss_sk, yss_sk)

print(model_lr_std.coef_)
print(model_lr_std.intercept_)
print(model_lr_std.score(xss_sk, yss_sk))

[[-0.49196281 -0.19145194]]
[1.1769986e-14]
0.28283042699952876

　偏回帰係数の差が、2.5倍程度と正規化無しのときと比べて小さくなっています。正規化してから求めた偏回帰係数のことを、標準化偏回帰係数と呼び回帰係数と区別します。また入力が正規化されているので切片model_lr.intercept_は（ほぼ）0となっています。1.1769986e-14と完全に0になっていないのはScikit-learnの計算上の都合です。ほとんど問題にならないですが、気になる場合はLinearRegression()にfit_intercept=Falseのオプションをつけて計算すると完全に0になります。一方、scoreに関しては、正規化しても変わりません。

　ここで、標準化偏回帰係数を用いて単純にxss_skを使ってyを計算（予測）すると、普通の回帰係数を用いて計算した結果と異なってしまい問題になります。

　実際に確認してみましょう。まず正規化無しで作成したモデルを使って予想します。これが本来求めたい値です。

model_lr.predict(x)

array([[ 9.93420409],
       [10.00689132],
       [10.08806511],
       ...,

　次に、正規化した後に作成したモデルを使って予測します。

model_lr_std.predict(xss_sk)

array([[-0.45880343],
       [-0.39057392],
       [-0.31437831],
       ...,

　本来求めたい値と大きく異なります。これだと実際に予測したいときに困ってしまいますね。

　この場合、正規化する前のモデルで逆変換して戻してあげる必要があります。scikit-learnには逆変換を行うinverse_transformがあるので、これを用いると簡単に変換できます。

sscaler.inverse_transform(model_lr_std.predict(xss_sk))

　結果は以下です。

array([[ 9.93420409],
       [10.00689132],
       [10.08806511],
       ...,

　本来求めたい値と一致しました。

　理解を深めるために、Numpyでも計算してみましょう。正規化するときと逆の計算をすればOKです。

model_lr_std.predict(xss_sk) * np.std(y.values) + np.mean(y.values)

array([[ 9.93420409],
       [10.00689132],
       [10.08806511],
       ...,

　こちらも、本来求めたい値と一致しました。

　今回は学習の理解を深めるために、入力変数を正規化してから計算しましたが、実は標準化偏回帰係数と偏回帰係数は、以下の簡単な式で変換できます。

\boldsymbol b_i^{\prime} = \boldsymbol b_i \sqrt \frac{S_{ii}}{S_{yy}}

$\boldsymbol b^{\prime}$ : i番目の標準化偏差回帰係数、 $\boldsymbol b$ : i番目の偏差回帰係数、 $S_{ii}$ : $x$のi番目の分散、 $S_{yy}$ : $y$の分散

参考： https://www.weblio.jp/content/標準化偏回帰係数

　偏差回帰係数から標準化偏差回帰係数にNumpyで計算して変換する場合は、以下の通りです。

b = model_lr.coef_ * ((x.apply(lambda x: x.var() / y.values.var()))**(0.5)).values

　結果は以下の通りです。

array([[-0.49211671, -0.19151183]])

　偏差回帰係数と計算した標準化偏差回帰係数と比較しましょう。

print(model_lr_std.coef_)
print(b)

　結果は以下の通りです。ほぼ一致しますね。細かい差は計算誤差だと思います。

[[-0.49196281 -0.19145194]]
[[-0.49211671 -0.19151183]]

　このように、偏差回帰係数と標準化偏差回帰係数は簡単に変換できるので、正規化しないで重回帰分析をして偏回帰係数を求め、後から必要に応じて標準化偏回帰係数を求める方が計算上は楽です。

正規化あり（min-maxスケーリング）

　次は、min-maxスケーリングした値で重回帰分析を行います。

model_lr_norm = LinearRegression()
model_lr_norm.fit(xms, yms)

print(model_lr_norm.coef_)
print(model_lr_norm.intercept_)
print(model_lr_norm.score(xms, yms))

[[-0.5820617  -0.25593116]]
[0.66805047]
0.28283042699952876

　同様に、yの値を予測するときには、逆変換をしてやる必要があります。

　min-maxスケーリングでも、標準化のときと同様inverse_transformを使って変換できます。

mscaler.inverse_transform(model_lr_norm.predict(xms))

　結果は以下です。

array([[ 9.93420409],
       [10.00689132],
       [10.08806511],
       ...,

　本来求めたい値と一致しました。Numpyでも計算してみましょう

model_lr_norm.predict(xms) * (np.max(y.values) - np.min(y.values)) + np.min(y.values)

array([[ 9.93420409],
       [10.00689132],
       [10.08806511],
       ...,

　こちらも、本来求めたい値と一致しました。

Numpyを使った重回帰分析

　次にscikit-learnを使わず、Numpyで重回帰分析を行います。単回帰分析の場合は、回帰係数は共分散と分散から計算できましたが、重回帰分析の場合は、偏回帰係数を以下の行列演算で計算します（以下の式では ${\boldsymbol b}$ が偏回帰係数です）。

\boldsymbol b = ({\boldsymbol X}^{\mathrm{T}} {\boldsymbol X})^{-1} {\boldsymbol X}^{\mathrm{T}} {\boldsymbol y}

　式の導出や説明などは、以下サイトを参照下さい。

　最初に、再度scikit-learnを使った重回帰での偏回帰係数の値を確認しましょう（x, yは標準化した値です）

model_lr_std.fit(xss_sk, yss_sk)

print(model_lr_std.coef_)

　以下は実行結果です。

[[-0.49196281 -0.19145194]]

　次に、Numpyで行列演算を行い計算します。@は行列の積です。逆行列を求めるlinalgモジュールはLAとしてimportするのが通例のようなので、ここではそれに倣います

from numpy import linalg as LA

LA.inv(xss_sk.T @ xss_sk) @ xss_sk.T @ yss_sk

　以下は実行結果です。

array([[-0.49196281],
       [-0.19145194]])

scikit-learnの値と一致しました。

なお、Numpyで逆行列が計算できないときは、LinAlgError: Singular matrix というエラーが発生します。

　無理やり計算したい場合は、微小な値を加えるといったテクニックが必要になります。Numpyで手軽に求める場合は以下のようにpinvを使えば計算は可能です。

np.linalg.pinv(xss_sk.T @ xss_sk) @ xss_sk.T @ yss_sk

　なお、今回は教科書的な式を計算しましたが、重回帰分析の計算は正規方程式 (normal equation) と呼ばれる以下の方程式を解くのが一般的です。詳細は、本記事コメント欄を参照下さい。

{\boldsymbol X}^{\mathrm{T}}{\boldsymbol X}{\boldsymbol b} = {\boldsymbol X}^{\mathrm{T}}{\boldsymbol y}

決定係数

　続いて決定係数$R$ を求めます。$R$が1に近いほど、xがyを説明できていることになります。

　決定係数は、単回帰のときと同様、全変動($S_{all}$)、回帰変動($S_{reg}$), 残差変動($S_{res}$)から計算できますが、入力変数が多くなるほど1に近づくので、入力変数が複数あるときは入力変数の数($p$)で補正する「自由度調整済み決定係数」$R_f$を用います。$S_{all}$, $S_{reg}$, $S_{res}$, $R_f$には以下のような関係があります。

\begin{eqnarray}
S_{all} &=& S_{reg} + S_{res}\\
R_f &=& 1 - \frac{S_{res}/(n-p-1)}{S_{all}/(n-1)}
\end{eqnarray}

　詳細は、以下サイトを参照下さい。

• https://bellcurve.jp/statistics/course/9706.html
• https://ja.wikipedia.org/wiki/%E6%B1%BA%E5%AE%9A%E4%BF%82%E6%95%B0

　ここから、Numpyで計算していきます。

　$S_{all}$の計算

s_all = ((yss_sk - yss_sk.mean())**2).sum()
print(s_all)

1599.0

　$S_{reg}$の計算

s_reg = ((model_lr_std.predict(xss_sk) - yss_sk.mean())**2).sum()
print(s_reg)

452.2458527722471

$S_{res}$の計算

s_res = ((yss_sk - model_lr_std.predict(xss_sk))**2).sum()
print(s_res)

　以下で計算した$S_{all}$と$S_{reg} + S_{res}$が等しいことを確認します。

print('Sall: %.3f' %s_all)
print('Sreg + Sres: %.3f' %(s_reg + s_res))

　以下は実行結果です。

Sall: 1599.000
Sreg + Sres: 1599.000

　以下の式より$R_f$を計算します。今回入力変数の数は2なので $p=2$となります。

R_f = 1 - \frac{S_{res}/(n-p-1)}{S_{all}/(n-1)}

1 - (s_res / (yss_sk.size - 2 - 1)) / (s_all / (yss_sk.size -1))

　以下は実行結果です。

0.28193171826143293

　単回帰の要領で、補正を行わずに決定係数を求めると、上記の値より少し値が大きくなっているのがわかります。

s_reg / s_all

0.2828304269995288

　今回は、入力変数の数が2なので、それほど差がないですが、入力変数が増えるほどこの差が広がっていきます。

相関行列

　次に入力変数の相関関係を確認するために、相関行列を求めます。

　詳細は以下サイト参照下さい。
https://algorithm.joho.info/programming/python/scikit-learn-datasets-load_diabetes/
http://zellij.hatenablog.com/entry/20130510/p1

　scikit-learnでは、以下のように相関行列を求めます。

import seaborn as sns

# 相関係数を計算
corr = np.corrcoef(xss_sk.T)

# 相関係数をヒートマップで可視化
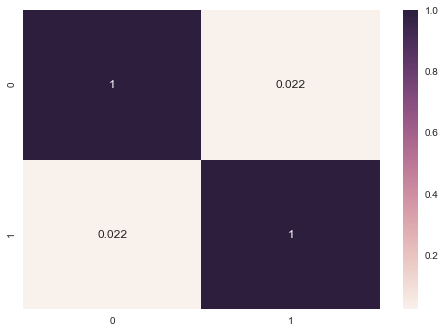
sns.heatmap(corr, annot=True)
plt.show()

　Numpyでは、入力変数の転置行列と入力の行列の積を計算して、対角行列が1になるようにスケーリングすると求められます

corr_np = (xss_sk.T) @ (xss_sk) / yss_sk.size

sns.heatmap(corr_np, annot=True)
plt.show()

　結果はscikit-learnで求めた値と同じになります。

　相関行列の対角以外の要素を相関係数と呼びます。相関係数が大きいと、変数間の相関が強く、変数間が独立ではない（線形従属）ことになります。この現象を「多重共線性」といいます。定量的には、行列の固有値を計算して確認できます。

w, v = LA.eig(corr)
print(w)

[1.02202623 0.97797377]

　このとき、相関行列の固有値の1部がほぼ0になると「多重共線性」となります。今回は、問題無いようです。
多重共線性になると、解が計算できなかったり、信頼性が低下してしまいます。そのため、高い相関値をもつ説明変数を取り除くなどの対策を取る必要があります。

多重共線性の対策

具体的には「正則化」と「次元削減」の2種類があり、それぞれ様々な手法があります。一部を紹介すると以下のようになります。

具体的な対策方法の紹介に関しては、またいずれ…

正則化

回帰係数が大きくなりすぎないように小さく抑える方法です。

具体的には、以下手法があります。

• リッジ回帰(Ridge Regression)
• L2正則化最小二乗法（q=2）

次元削減

　大きく、特徴を選択する方法（1部の入力変数のみを使用する、不要な入力変数を削除する）と特徴を抽出する方法（複数の変数を1つにまとめる、変換する）の2つがあります。それぞれの手法を紹介します。

特徴選択

• LASSO

特徴を抽出する

• 主成分分析

統計的な解釈

　最後に、単回帰のときと同様に統計的な解釈を行います。ここは、statsmodelというライブラリを使って一気にやってしまいます。

import statsmodels.api as sm

x_add_const = sm.add_constant(xss_sk)
model_sm = sm.OLS(yss_sk, x_add_const).fit()
print(model_sm.summary())

　以下が実行結果です。

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.283
Model:                            OLS   Adj. R-squared:                  0.282
Method:                 Least Squares   F-statistic:                     314.7
Date:                Wed, 11 Sep 2019   Prob (F-statistic):          6.11e-116
Time:                        17:03:00   Log-Likelihood:                -2003.1
No. Observations:                1599   AIC:                             4012.
Df Residuals:                    1596   BIC:                             4028.
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const       1.191e-14      0.021   5.62e-13      1.000      -0.042       0.042
x1            -0.4920      0.021    -23.202      0.000      -0.534      -0.450
x2            -0.1915      0.021     -9.029      0.000      -0.233      -0.150
==============================================================================
Omnibus:                      157.571   Durbin-Watson:                   1.494
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              216.102
Skew:                           0.778   Prob(JB):                     1.19e-47
Kurtosis:                       3.908   Cond. No.                         1.02
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

　今まで求めた、モデル関数の回帰変数、切片、決定係数等、今まで求めた値がずらっと表示されています。

　その他の値の意味は今回は省略します（力尽きました）

まとめ

　重回帰分析に関して学びました。

　文章への編集リクエスト、コードへのPull Requestお待ちしております。

　次回は、「ロジスティック回帰分析」の予定です。

次回：Pythonで基礎から機械学習 「ロジスティック回帰分析」

参考

• https://alexandco-python.tokyo/archives/240
• https://openbook4.me/projects/183/sections/1366
• https://www.enisias.cloud/machine-learning/526/
• https://qiita.com/yossyyossy/items/ac6961ca5a0e765f56be
• https://qiita.com/avengers_/items/faa735ae0db9655b2ea9
• http://www.snap-tck.com/room04/c01/stat/stat07/stat0701.html
• http://short4010.hatenablog.com/entry/2018/03/01/222721
• https://qiita.com/seno/items/14fad1ef792e48f4d4d6
• https://qiita.com/ynakayama/items/36b7c1640e6a02ce2e00
• https://omedstu.jimdo.com/2018/04/21/重回帰分析①/
• http://tekenuko.hatenablog.com/entry/2019/08/27/003505