ブログの目的
- 線形回帰モデルの理論的背景がクリアになってきたので、手始めに重回帰分析の導入を備忘録として投稿します
- 最終的にPython の Numpy でアルゴリズムを記述し、結果をscikit-learnと比較してみます
- 重回帰分析のアルゴリズムに関しては下記の書籍で学習しました
- 機械学習のエッセンス- (Machine Learning) 単行本 著者; 加藤公一 出版社; SBクリエイティブ
- ベクトルの微分公式についてはQiitaの以下の記事に分かりやすくまとめられていました
- 参考 「ベクトルで微分・行列で微分」公式まとめ
アルゴリズムの導入
準備
まず、以下のおなじみ3つについて定義をします
- 説明変数$x_1, x_2, x_3, \cdots, x_m$を$\boldsymbol{x}$($x$のベクトル)とする
- 予測値を$\hat{y}$とする($\hat{y}$はスカラー)
- 回帰係数を$w_1, w_2, w_3, \cdots, w_m$を$\boldsymbol{w}$($w$のベクトル)をする
この時、目的変数は以下の式で表すことができます
$$\hat{y}=w_1x_1 + w_2x_2 + \cdots + w_mx_m$$
一般に重回帰分析には切片もあるので、ここでは便宜的に以下の通りに表します。(単独に足すこともできますが、下記の方が計算が楽になります)
$$\hat{y}= w_0x_0 + w_1x_1 + w_2x_2 + \cdots + w_mx_m$$
$$(w_0 ,切片 : x_0=1)$$
ベクトルで表すと以下の通りになります。$x$は横ベクトルなので、転置の記号で表しています
\hat{y} = (\begin{array} xx_0&x_1&\cdots&x_m \end{array})
\begin{pmatrix}
w_0 \\
w_1 \\
\vdots \\
w_m \\
\end{pmatrix}
$$\boldsymbol{\hat{y}} = \boldsymbol{x}^T \boldsymbol{w}$$
重回帰分析では、$x$ベクトルは一つではありません。多数の教師データから、回帰係数を予測します。よって、$x$横ベクトルをサンプル数だけ縦方向に並べた行列を$X$とします。また、教師データの数だけ予測値も出てくるので、その値を並べたベクトルを$y$ベクトルと定義します。式で表した方が分かりやすいと思います。サンプル数を$n$として式に表してみます。
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix} = \begin{pmatrix}
x_{01} & x_{11} & x_{21} & \cdots & x_{m1} \\
x_{02} & x_{12} & x_{22} & \cdots & x_{m2} \\
\vdots & \vdots & \ddots & \ddots & \vdots \\
x_{0n} & \cdots & \cdots & \cdots & x_{mn}
\end{pmatrix}
\begin{pmatrix}
w_0 \\
w_1 \\
w_2 \\
\vdots \\
w_m
\end{pmatrix}
$$\boldsymbol{\hat{y}} = X\boldsymbol{w}\cdots ⑴$$
すごくスッキリした形になりました。線形代数おそるべしです
損失関数の導入
予測値$\hat{y}$と実際の$y$に隔離が無いように、重み$w$を求めて行きますが、重回帰分析では最小二乗法を使います。ここでは最小二乗法については触れません。
最小二乗法では以下の通りに表される損失関数$L$を最小化させる様に重みを決定します。
$$L=\sum_{i=1}^{n}(y_i - \hat{y_i})^2$$
$y_i - \hat{y_i}$ について $\hat{y}$ベクトルと $y$ベクトルの成分同士の引き算と見ることができると思います。
上式をベクトルの積の形で表すと以下の様になります。
(\begin{array} yy_1 - \hat{y_1}&y_2 - \hat{y_2} &\cdots&y_n - \hat{y_n} \end{array})
\begin{pmatrix}
y_1 - \hat{y_1} \\
y_2 - \hat{y_2} \\
\vdots \\
y_n - \hat{y_n}
\end{pmatrix}
$$ (\boldsymbol{y} - \boldsymbol{\hat{y}})^T(\boldsymbol{y} - \boldsymbol{\hat{y}})$$
尚、上の式を別の表現で表すと$(\boldsymbol{y} - \hat{y})$ベクトルのL2ノルムの2乗と言います。式で表すと下記の通りになります。L2ノルムは高校生の頃にベクトルの長さを求める時に習ったあれです。
$$ ||\boldsymbol{y} - \boldsymbol{\hat{y}}||^2 $$
式変形とベクトルの偏微分
上記の式と先ほどの⑴式から以下の通りに損失関数を導くことができます
$$ L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
$$ L = (\boldsymbol{y}^T - \boldsymbol{w}^T X^T)(\boldsymbol{y} - X\boldsymbol{w})$$
$$ L = \boldsymbol{w} ^T X^T X \boldsymbol{w} - \boldsymbol{w} ^T X^T \boldsymbol{y} - \boldsymbol{y}^T X \boldsymbol{w} + \boldsymbol{y}^T \boldsymbol{y} $$
ここで第2項は第3項を転置して更に転置している第2項と第3項は転置の関係にある。また横ベクトル×行列×縦ベクトルの形からスカラーであることが分かる。よって(スカラー)^T=スカラーであることから同値(詳細はこちら→高校数学の美しい物語、自分で手を動かして確かめてみると納得するかと思います)
$$ L = \boldsymbol{w} ^T X^T X \boldsymbol{w} - 2\boldsymbol{y}^T X \boldsymbol{w} + \boldsymbol{y}^T \boldsymbol{y} $$
この式を$\boldsymbol{w}$の各成分で偏微分した、一次導関数が0となる$w$を求めます。つまり損失関数$L$をベクトル$w$で微分します。ベクトルの微分公式は冒頭であげたリンクを参考にしてください。第1項が行列をベクトルで微分、第2項がベクトルをベクトルで微分、第3項がスカラーをベクトルで微分しています。
$$ \frac{\partial L}{\partial \boldsymbol{w}} = 2X^T X \boldsymbol{w} - 2X^T \boldsymbol{y} + O $$
$\frac{\partial L}{\partial \boldsymbol{w}} = 0$とすると
$$ 2X^T X \boldsymbol{w} = 2X^T \boldsymbol{y}$$
今、$X^T X$は正方行列であり逆行列が存在するため
$$ \boldsymbol{w} = (X^T X)^{-1} X^T \boldsymbol{y} $$
ようやく求めるべき$\boldsymbol{w}$が分かりました。
Pythonでの実装
まずは普通にscikit-learnでモデルを作ってみます。環境はJupyter Notebookです
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
boston = load_boston()
X, y = boston.data, boston.target
clf1 = LinearRegression().fit(X, y)
coef_df = pd.DataFrame(clf1.coef_,
index=boston.feature_names,
columns=['clf1'])
coef_df

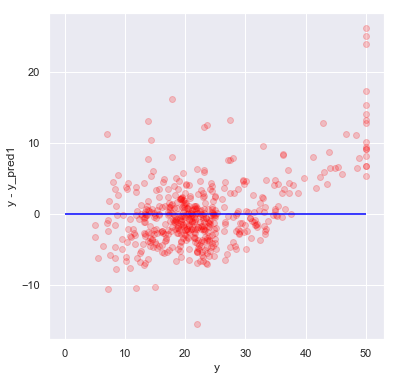
# 横軸がy(実際値)、縦軸がy-y_pred(誤差)
y_pred1 = clf1.predict(X)
plt.figure(figsize=(6, 6))
plt.hlines([0], min(y)-5, max(y) , color='blue')
plt.scatter(y, y - y_pred1, color='red', marker='o', alpha=0.2)
plt.xlabel('y')
plt.ylabel('y - y_pred1');
次は、先ほど導いた式を使って、重回帰分析のクラスを実装してみます
class LinearReg2:
def __init__(self):
self.w_ = None
def fit(self, X, t):
# 先頭列に1を追加
# 追加の理由は先ほどの説明を参照(切片の計算のため)
X = np.insert(X, 0, 1, axis=1)
self.w_ = np.linalg.inv(X.T @ X) @ X.T @ y
def predict(self, X):
X = np.insert(X, 0, 1, axis=1)
return X @ self.w_
先ほどのモデルと回帰係数を比較してみます
clf2 = LinearReg2()
clf2.fit(X, y)
coef_df['clf2'] = clf2.w_[1:]
coef_df

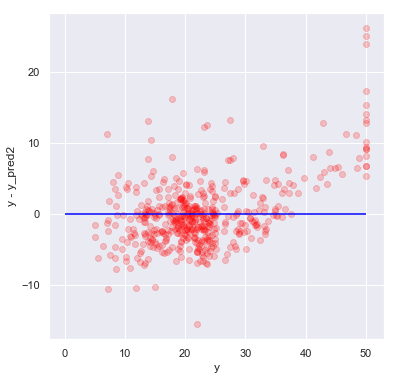
一致していることが分かりました。もちろん予測値もあっていることが確認できます
# 横軸がy(実際値)、縦軸がy-y_pred(誤差)
y_pred2 = clf2.predict(X)
plt.figure(figsize=(6, 6))
plt.hlines([0], min(y)-5, max(y) , color='blue')
plt.scatter(y, y - y_pred2, color='red', marker='o', alpha=0.2)
plt.xlabel('y')
plt.ylabel('y - y_pred2');
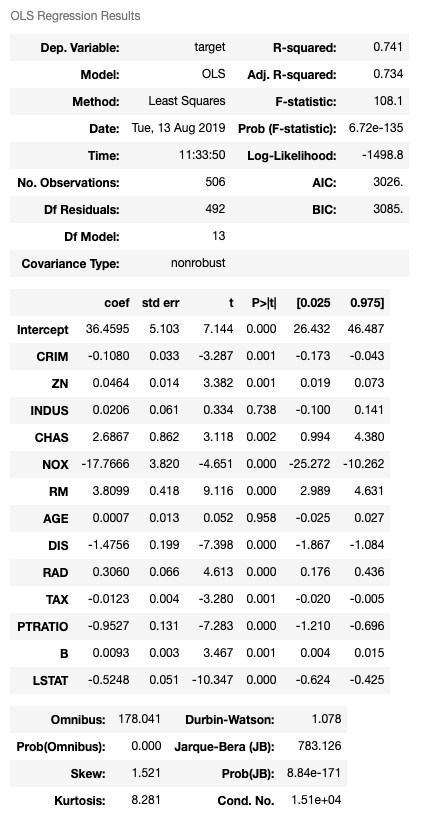
尚、statsmodelsの結果でも一致している事が分かります。(coefの部分)
import statsmodels.api as sm
df = pd.DataFrame(boston.data, columns=boston.feature_names)
clf3 = sm.OLS(boston.target, sm.add_constant(df)).fit()
clf3.summary()