目的
学習用データとしてsklearnのデータセットをつかって、重回帰分析をしてみようと思います!
ざっくり説明しますと、「いろいろなデータを使って住宅価格予測しちゃおう!」というものです。
準備するもの
・anacondaの中身(python3系、scikit-learn、matplotlib、numpy)
・パソコン(僕はmac 2016 lateですが、重い処理はしないので動けば大丈夫です)
・後で下にある覚えておくとわかりやすい用語集をちょっと見てみてください。
anacondaのセットアップは割愛します!
インストールして動かない場合は「anacondaのpathの通し方」を参照してみてくださいね。
覚えておくとわかりやすい用語集!
そもそも機械学習
・説明変数を元に、目的変数を当てるモデルを作成することを機械学習といいます。
機械学習のモデルは大きく分けて「教師あり学習」と「教師なし学習」があります。
「教師あり学習」はお手本となる「教師データ」を用意し,
そのデータに沿って,将来起こりそうな事象を予測します。
参考: @m-hayashi さん:【【機械学習】シンプルな回帰分析の例】
今回の場合はデータを使って住宅価格を予測します!
説明変数と目的変数
m-hayashiさんのおっしゃるように、将来の予測出来るのが機械学習です。
そのときに、予測する対象(今回の場合は住宅価格)を目的変数と呼びます!
それに対して説明変数は、目的を予測するためのデータ(後で説明しますが、今回の場合は犯罪率や部屋の数などになります)です。
教師有り、教師なし学習
機械学習のサービスの大半は、この「教師あり学習」のモデルです。
「教師なし学習」は判断するための教師データはありません。
解析対象のデータに存在する特徴を探し出し、データの似た者同士を
グループ分けする用途で使用されます。
参考: @m-hayashi さん:【【機械学習】シンプルな回帰分析の例】
早速分析していきます!🏃
必要なライブラリとデータセットを呼びます
# 必要なライブラリを呼びます
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import matplotlib.pyplot as plt
%matplotlib inline
sklearn.datasetsからデータセット(boston)を呼びます
from sklearn.datasets import load_boston
変数に入れて、printしてみます
boston = load_boston()
print(boston)
"""
{'feature_names': array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'],
dtype='<U7'), 'data': array([[ 6.32000000e-03, 1.80000000e+01, 2.31000000e+00, ...,
1.53000000e+01, 3.96900000e+02, 4.98000000e+00],
[ 2.73100000e-02, 0.00000000e+00, 7.07000000e+00, ...,
1.78000000e+01, 3.96900000e+02, 9.14000000e+00],
[ 2.72900000e-02, 0.00000000e+00, 7.07000000e+00, ...,
1.78000000e+01, 3.92830000e+02, 4.03000000e+00],
...,
[ 6.07600000e-02, 0.00000000e+00, 1.19300000e+01, ...,
2.10000000e+01, 3.96900000e+02, 5.64000000e+00],
[ 1.09590000e-01, 0.00000000e+00, 1.19300000e+01, ...,
2.10000000e+01, 3.93450000e+02, 6.48000000e+00],
[ 4.74100000e-02, 0.00000000e+00, 1.19300000e+01, ...,
2.10000000e+01, 3.96900000e+02, 7.88000000e+00]]), 'DESCR': "Boston House Prices dataset\n===========================\n\nNotes\n------\nData Set Characteristics: \n\n :Number of Instances: 506 \n\n :Number of Attributes: 13 numeric/categorical predictive\n \n :Median Value (attribute 14) is usually the target\n\n :Attribute Information (in order):\n - CRIM per capita crime rate
・
・
・
ながいのでココらへんまで!
"""
よくわからないとおもうんですが、これからわかりやすいようにCSVにしていきます。
データセットの説明を読む
print(boston.DESCR)
"""
Boston House Prices dataset
===========================
Notes
------
Data Set Characteristics:
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive
:Median Value (attribute 14) is usually the target
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
-
・
・
・
"""
DESCRはdescription(説明)の略ですね!
※他にもsklearnにはたくさんのデータセットがあるんですが、この文法が使えるデータセットと使えないのがあるみたいです。
CSVにします
print(boston.data)
"""
[[ 6.32000000e-03 1.80000000e+01 2.31000000e+00 ..., 1.53000000e+01
3.96900000e+02 4.98000000e+00]
[ 2.73100000e-02 0.00000000e+00 7.07000000e+00 ..., 1.78000000e+01
3.96900000e+02 9.14000000e+00]
[ 2.72900000e-02 0.00000000e+00 7.07000000e+00 ..., 1.78000000e+01
3.92830000e+02 4.03000000e+00]
...,
[ 6.07600000e-02 0.00000000e+00 1.19300000e+01 ..., 2.10000000e+01
3.96900000e+02 5.64000000e+00]
[ 1.09590000e-01 0.00000000e+00 1.19300000e+01 ..., 2.10000000e+01
3.93450000e+02 6.48000000e+00]
[ 4.74100000e-02 0.00000000e+00 1.19300000e+01 ..., 2.10000000e+01
3.96900000e+02 7.88000000e+00]]
"""
print(boston.feature_names)
# DESCRで見た時に表示されたカラム名です。
"""
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
"""
# データフレームの引数にboston.dataを入れます
# 詳しい使い方を見たい方は以前の投稿を見てください!
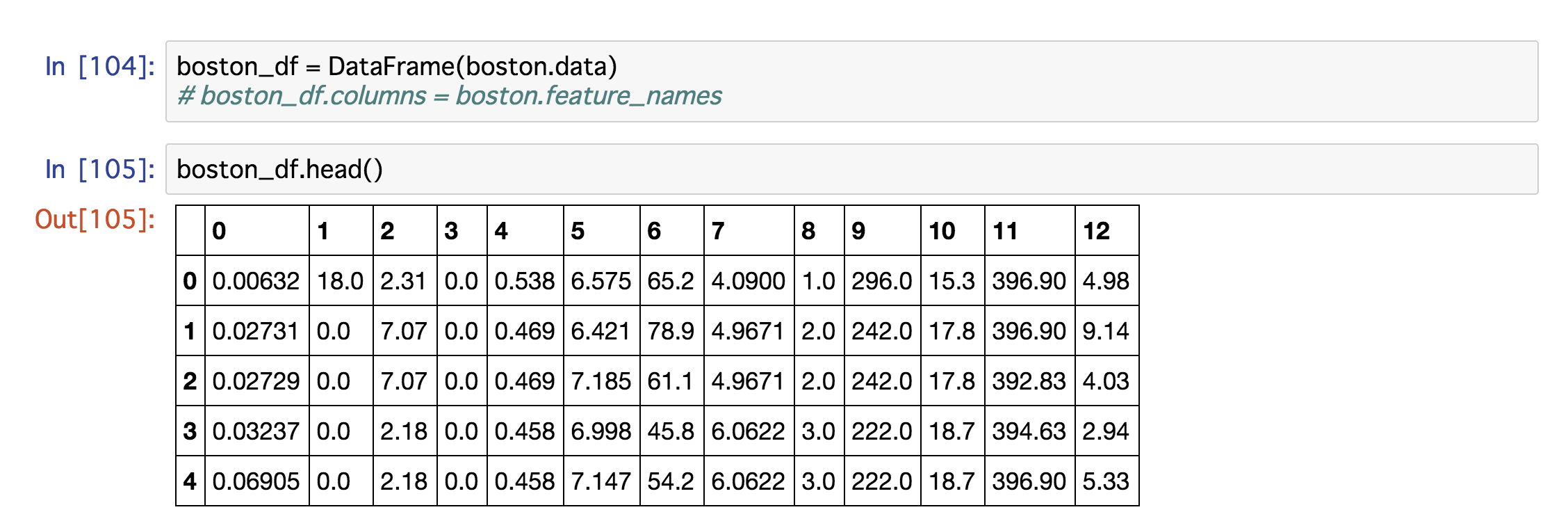
boston_df = DataFrame(boston.data)
# カラムに先程のboston.feature_namesを指定します。
boston_df.columns = boston.feature_names
大きく分けると、boston.dataに値が入っていて、boston.feature_namesにカラム名が入っています!
これだけだとなんの数字かわかりませんね。。。
このように、厳密にはCSVではないのですが、DataFrameに要素と値を入れるとCSVっぽく扱えます!
※CSVにするには、このように書きます!
boston_df.to_csv("csvにしたいなまえ.csv")
拡張子をcsvにすることをお忘れなく!
headでcsvを見てみましょう!
boston_df.head()
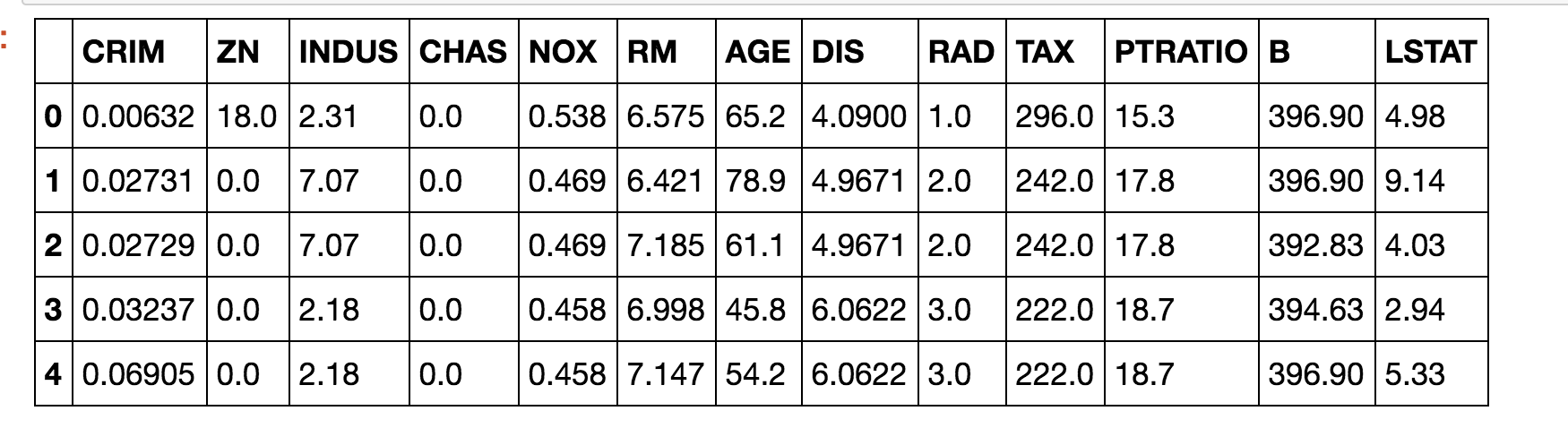
ちなみにカラムを指定しないと、なんのデータ見ているのかさっぱりわからないです
カラムを指定しない場合
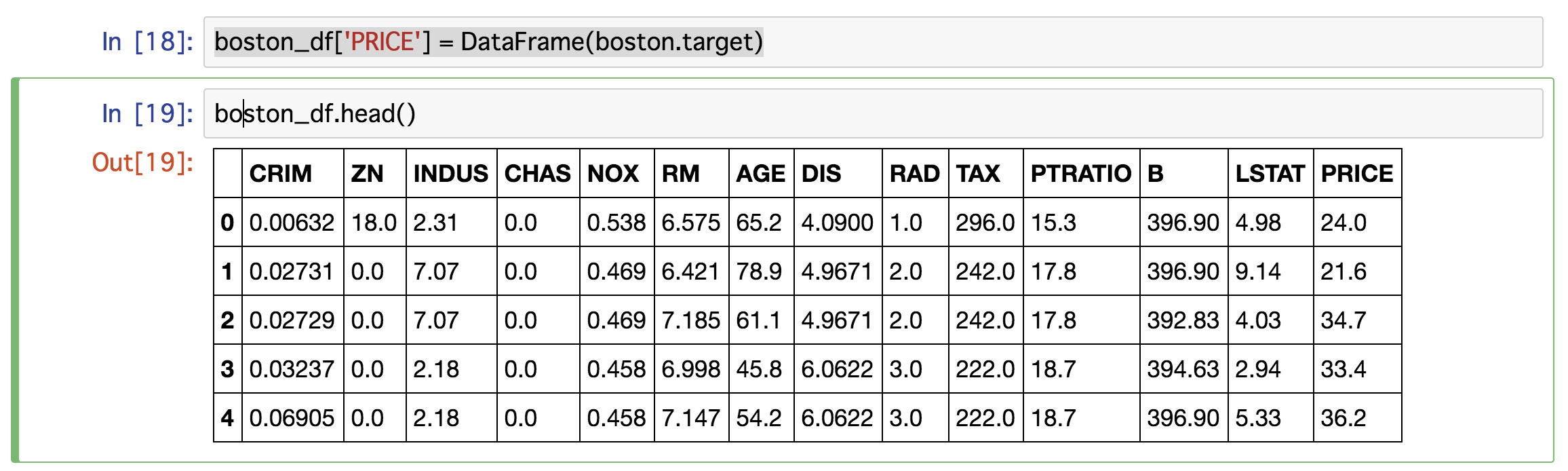
最後に、説明変数となる住宅価格を追加
boston_df['PRICE'] = DataFrame(boston.target)
これでデータの下準備はおわりましたー!
👼👼👼ここから重回帰!👼👼👼
主に使うのはsklearn(エスケーラーン、サイキットラーン)というオープンソースライブラリです。
機械学習にもつかいます!
今からやることは
①まずは、boston_df全体を使って、目的変数(Yとします)、説明変数(Xとします)をつかい重回帰分析をします!その後、係数を見ることで、どのカラム(データの要素)が重要なのか調べます。
②目的変数(Yとします)、説明変数(Xとします)ともにboston_dfからデータをランダムに分けて、テスト用データをどれくらいの精度(寄与率)で予測できるモデルを作れたか知りたいと思います!
その前に、基本的な文法!
# インスタンス(モデルの元)を作成します!
変数 = LinearRegression()
# fitで説明変数、目的変数を元にモデルを作成します
# 第一引数に説明変数、第二引数に目的変数を入れます!
さっき作った変数(モデル).fit(X,Y)
# scoreを使って、精度を求める
# ②で作成する、予想用データ等を引数に入れます。
さっき作った変数(モデル).score(X,Y)
①をやってみよう!
boston_dfには目的変数も入っているので、XとYという名前で別々なDFを作ります!
# インスタンス
linear_regression = LinearRegression()
# 説明変数を縦(1)の列と指定して削除します!
X = boston_df.drop("PRICE", 1)
# Yに目的変数を入れます!
Y = boston_df.PRICE
# こんな書き方でも大丈夫!
# Y = boston_df["PRICE"]
それぞれ中身を確認!
X.head()
Y.head()
"""
0 24.0
1 21.6
2 34.7
3 33.4
4 36.2
5 28.7
6 22.9
7 27.1
8 16.5
9 18.9
10 15.0
11 18.9
12 21.7
13 20.4
14 18.2
15 19.9
16 23.1
17 17.5
18 20.2
19 18.2
20 13.6
21 19.6
22 15.2
23 14.5
24 15.6
25 13.9
26 16.6
27 14.8
28 18.4
29 21.0
...
"""
無事予想通りのデータを作成できましたでしょうか!
早速重回帰
# 通常であれば行列の計算などが必要ですが、簡単にやってくれます。
linear_regression.fit(X,Y)
次に、どのカラムが説明変数に大きい影響を与えたか、係数を元に調べましょう
print(linear_regression.coef_)
"""
[-1.07170557e-01 4.63952195e-02 2.08602395e-02 2.68856140e+00
-1.77957587e+01 3.80475246e+00 7.51061703e-04 -1.47575880e+00
3.05655038e-01 -1.23293463e-02 -9.53463555e-01 9.39251272e-03
-5.25466633e-01]
"""
わかりずらいので、データフレームにします。
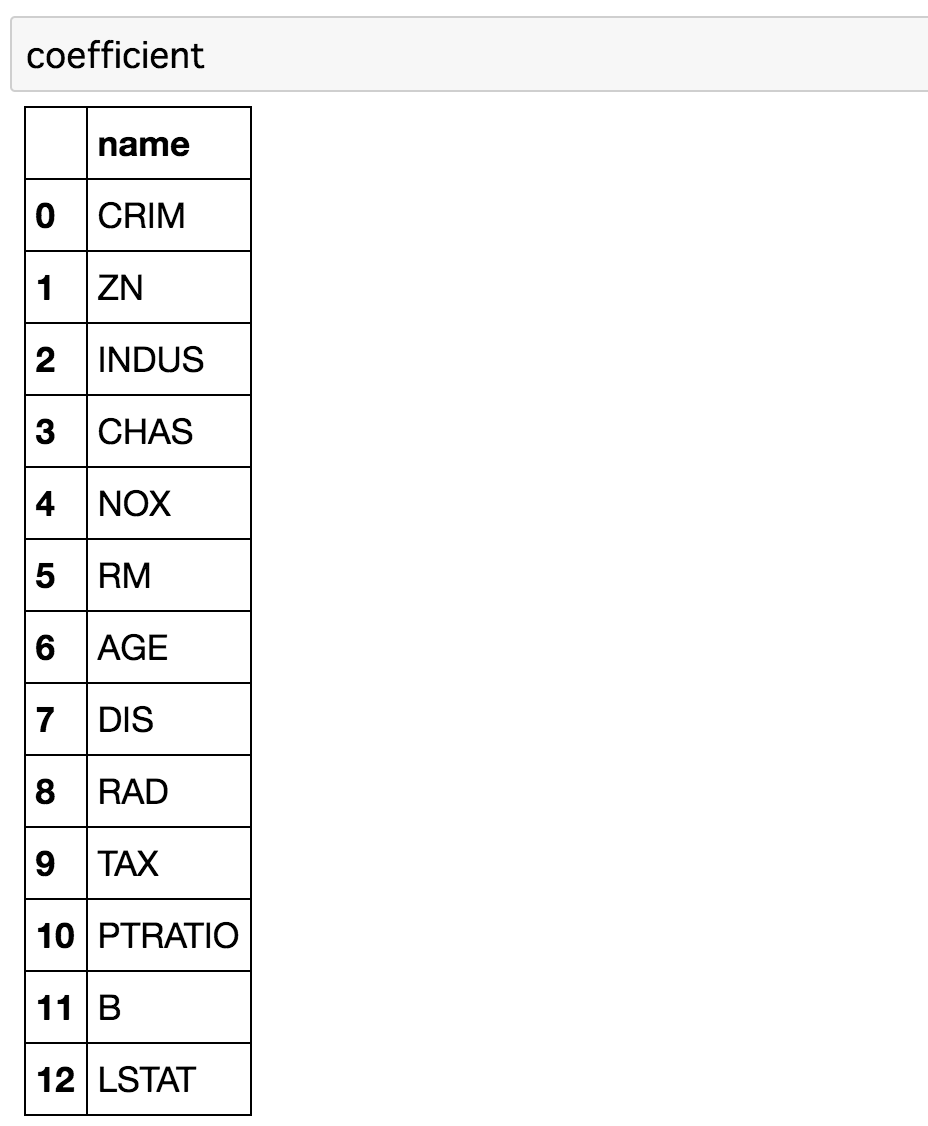
# 先程のfeature_namesをデータフレームに入れます。
coefficient['f_names'] = DataFrame(boston.feature_names)
coefficient
# 次に、係数(coefficient)を入れます
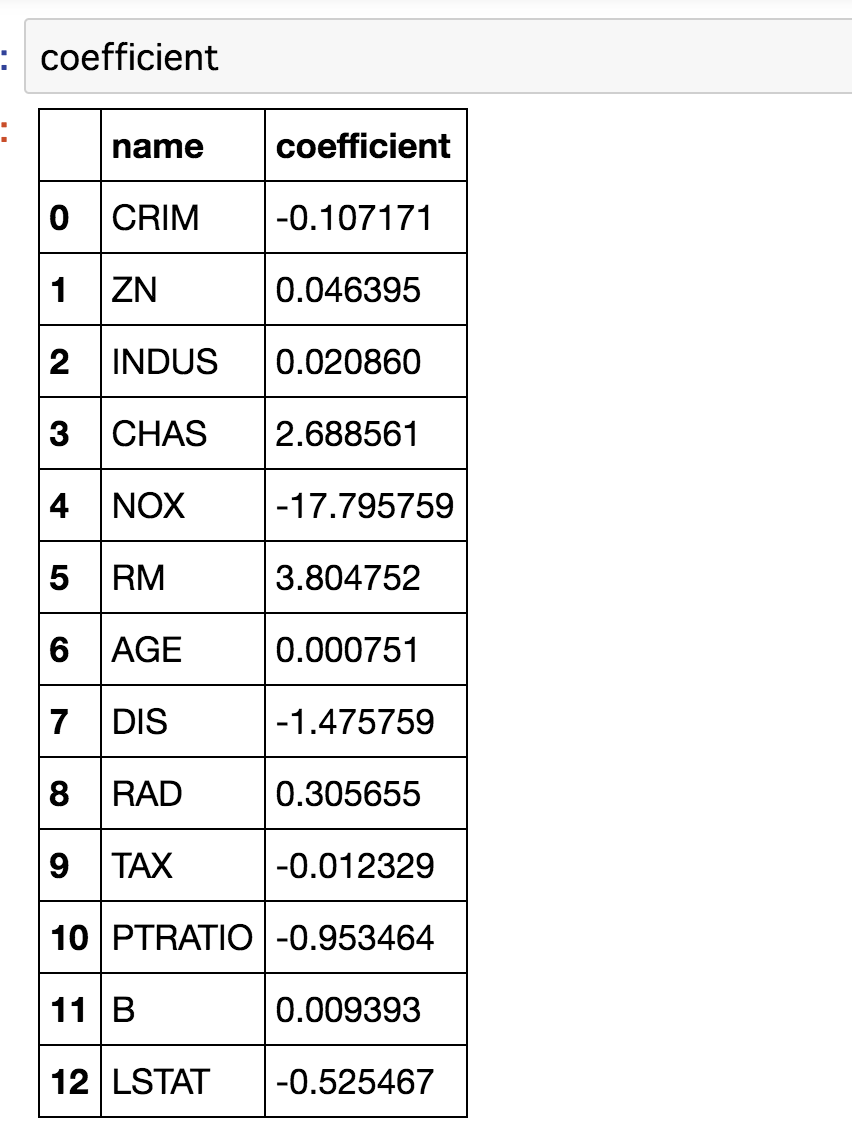
coefficient['coefficient'] = DataFrame(linear_regression.coef_)
coefficient
切片より、CHAS(チャールズリバー川に面しているかどうかのダミー変数です)とRM(room(部屋の数))が住宅価格に
大きな影響をあたえることがわかりました!!!!
ちなみに、切片(intercept)はこのようにして求めることが出来ます。
linear_regression.intercept_
"""
36.491103280363404
"""
※y = ax + ax ... ax + bのうちのbになります。
ちなみに、この重回帰が自由度調整済みなのかは不明です。。。。
②をやってみる.
ランダムにサンプルを分けるために、sklearn.cross_validation(または、model_selection)をimportします。
エラーが出て気になる方は、model_selectionを使いましょう!
# サンプルをランダムに分けるcross_validation
# import sklearn.cross_validation
import sklearn.model_selection
# 左辺にモデル構築用のXY,テスト用のX,Yを用意します。
# 先ほど作成した、説明変数を第一引数に、目的変数を第二引数に置きます。
# train_test_splitを足すことを忘れないでください!!
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X,Y)
# cross_validation
# X_train, X_test, Y_train, Y_test = sklearn.cross_validation.train_test_split(X,Y)
先程までのXとtrain,testのXのデータの長さを比べてみましょう!
X_test.shapne
X_train.shape
X.shape
先程と同様に、インスタンスを作成してfitを使い学習させます。
# 線形回帰モデルを作成
multi_lreg = LinearRegression()
# X,Y双方がtrain用のデータである点にご注意ください。
multi_lreg.fit(X_train, Y_train)
寄与率(決定係数)を算出して、モデルの正確性を数字で調べよう!
scoreを使い、結果を評価してみます。
# トレーニングに使用したデータセットでの精度
print(multi_lreg.score(X_train,Y_train))
"""
0.73734258077086
"""
# テストに使用したデータセットでの精度
print(multi_lreg.score(X_test,Y_test))
"""
0.7425657307269696
"""
1に近いほど、精度が高いということになります!
重回帰の場合、50%が精度の目安だと言われているので、まずまずの結果なのではないでしょうか!
最後に
私事ですが、転職してB to Cプラットフォームを提供するECベンチャーへ転職しました!
まだまだ努力が足りませんが、少しづつ進んでいるのでそれで良いんじゃないかなと思います。
人生積み木だなーとつくづく思います。