More than 1 year has passed since last update.

Pythonで基礎から機械学習「単回帰分析」

Last updated at 2023-08-14Posted at 2019-09-04

はじめに

　この「Pythonで基礎から機械学習」シリーズの目的や、環境構築方法、シリーズの他の記事などは以下まとめページを最初にご覧下さい。

　本記事は、初学者が自分の勉強のために個人的なまとめを公開している記事になります。そのため、記事中に誤記・間違いがある可能性が大いにあります。あらかじめご了承下さい。

　より良いものにしていきたいので、もし間違いに気づいた方は、編集リクエストやコメントをいただけましたら幸いです。

　本記事のコードは、Google Colaboratory上での実行を想定しています。本記事で使用したGoogle ColabのNotebookは以下となります。

01_linear_regression.ipynb

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}

単回帰分析

　初回は、データ分析の基礎中の基礎の単回帰分析をPythonを使って手を動かしながら実行していきます。
単回帰はExcelを使えば簡単にできてしまうのですが、もっと複雑な機械学習手法の基礎となるので、Pythonを使ったデータ分析の練習としてあえてPythonを使います。
　scikit-learnを使えば一発で式は求まるのですが、今回はそれだけでなく、Numpyを使って実際に値を導出しながら、その値が持つ意味を確認していきます。

　単回帰分析に関して、参考にしたサイトは本記事の最後に列挙しました。書籍に関しては、冒頭のまとめページを参照下さい。

データの読み込みと可視化

　ここでは、pandasというデータ処理を行うライブラリとmatplotlibというデータを可視化するライブラリを使って、分析するデータがどんなデータかを確認します。

　まずは、以下コマンドで、今回解析する対象となるデータをダウンロードします。

!wget https://raw.githubusercontent.com/karaage0703/machine-learning-study/master/data/karaage_data.csv

　次に、pandasで分析するcsvファイルを読み込み、ファイルの中身の冒頭部分を確認します。

　pandas, matplotlibなどのライブラリの使い方に関しては、以下ブログ記事を参照下さい。
Python/pandas/matplotlibを使ってcsvファイルを読み込んで素敵なグラフを描く方法（Mac/Raspberry Pi）

import pandas as pd

df = pd.read_csv('karaage_data.csv')
df.head()

　このデータは、お祭りの来場者に対する、からあげ屋さんの出店の数という架空のデータです。

　xが来場者[万人] yがからあげ屋さんの出店の数を表しています。例えば、1万人のお祭りだとからあげ屋さんは2つ。10万人のお祭りだとからあげ屋さんは3つという感じです。

　x列、y列にある値を x, y に格納します。今後この、x, y の値を分析していきます。

x = df[['x']]
y = df[['y']]

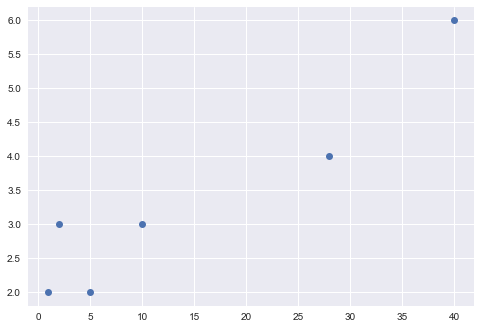
まずは、x, yをグラフで可視化します。matplotlibというライブラリを使います。

import matplotlib.pyplot as plt
import seaborn as sns

plt.plot(x, y, 'o')
plt.show()

お祭りの来場者(x)が増えるほど、からあげの出店数が増えているのがなんとなく見えますね。

scikit-learnを使った単回帰分析

　早速、単回帰分析をしていきます。まずは、scikit-learnというライブラリでPythonの実力を体感します。

from sklearn.linear_model import LinearRegression

model_lr = LinearRegression()
model_lr.fit(x, y)

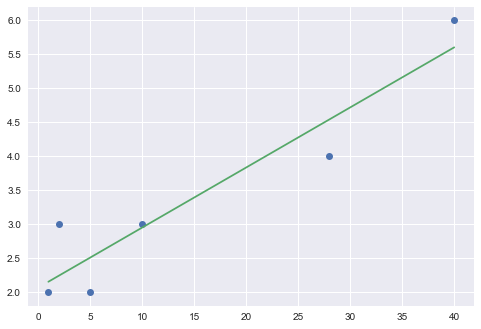
　これで、完了です。一瞬ですね。早速結果を可視化します

import matplotlib.pyplot as plt
import seaborn

plt.plot(x, y, 'o')
plt.plot(x, model_lr.predict(x), linestyle="solid")
plt.show()

print('モデル関数の回帰変数 w1: %.3f' %model_lr.coef_)
print('モデル関数の切片 w2: %.3f' %model_lr.intercept_)
print('y= %.3fx + %.3f' % (model_lr.coef_ , model_lr.intercept_))
print('決定係数 R^2： ', model_lr.score(x, y))

また、以下がそれぞれ、回帰係数、切片、決定係数です

モデル関数の回帰変数 w1: 0.088
モデル関数の切片 w2: 2.066
y= 0.088x + 2.066
決定係数 R^2：  0.8844953173777316

　単回帰ができてしまいました。

　これで完了！でも良いのですが、それぞれの数字の意味や求め方をNumpyを使って計算していきましょう。

Numpyを使った単回帰分析

　ここから、Scikit-learnを使わず、Numpyを使った単純な計算で単回帰分析を行い、その意味を解きほぐしていきましょう。

　単回帰分析の解の導出には、最小二乗法を用います。具体的には、モデルから予測した値と実際の値との二乗和誤差を最小にするような解を求めます。数式としては以下となります。

\hat{w_0}, \hat{w_1} = \argmin_{w_0, w_1} \sum_{i=1}^{n} (y_i - w_0 - w_1 x_i)^2

　数式の記号（$\argmin$ , $\hat{w_0}$等）の意味がよく分からないという人は、以下記事参照下さい。

機械学習関係の論文を読み書きするための数式・記号まとめ

　ここから、最小二乗解を導出していきます。まずは、最小二乗和を以下のように定義します。

S = \sum_{i=1}^{n} (y_i - w_0 - w_1 x_i)^2

　この値が最小化になる解は、すなわち偏微分したら0になる点なので、以下の連立方程式を解けばOKです。

\begin{align}
\frac{\partial S}{\partial \hat{w_1}} &= \sum_{i=1}^{n} (-2 x_i)(y_i - \hat{w_0} - \hat{w_1} x_i) = 0 \\
\frac{\partial S}{\partial \hat{w_0}} &= \sum_{i=1}^{n} (-2)(y_i - \hat{w_0} - \hat{w_1} x_i) = 0
\end{align}

　計算していきます。下の式を(-2)で割ります。

\sum_{i=1}^{n} y_i - \sum_{i=1}^{n} \hat{w_0} - \sum_{i=1}^{n} \hat{w_1} x_i  = 0

　ここで $\sum_{i=1}^{n} x_i$ は $x$の平均$\bar{x}$を使って以下のように表せます。

\sum_{i=1}^{n} x_i = n \bar{x}

n \bar{y} - n \hat{w_0} - \hat{w_1} n \bar{x} = 0 \\
\hat{w_0} = \bar{y} - \hat{w_1} \bar{x}

　これを連立方程式の上の式に代入して(-2）で割ります。

\sum_{i=1}^{n} x_i y_i - (\bar{y} - \hat{w_1} \bar{x}) \sum_{i=1}^{n} x_i -  \hat{w_1} \sum_{i=1}^{n} x_i^2 = 0 \\
\sum_{i=1}^{n} x_i y_i - \bar{y} \sum_{i=1}^{n} x_i - \hat{w_1}( \sum_{i=1}^{n} x_i^2 - \bar{x} \sum_{i=1}^{n} x_i) = 0 \\
(\sum_{i=1}^{n} x_i y_i - n \bar{x} \bar{y}) - \hat{w_1}( \sum_{i=1}^{n} x_i^2 - n \bar{x}^2) = 0 \\
\hat{w_1} = \frac{\sum_{i=1}^{n} x_i y_i - n \bar{x} \bar{y}}{\sum_{i=1}^{n} x_i^2 - n \bar{x}^2} \\
\hat{w_1} = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}( x_i - \bar{x})^2}

　ここで$x$,$y$の共分散($S_{xy}$) と$x$の分散($S_{xx}$)を用いて、$\hat{w_1}$は以下のように表せます。

\begin{align}
\hat{w_1} &= \frac{S_{xy}}{S_{xx}} \\
S_{xx} &= \sum_{i=1}^{n}( x_i - \bar{x})^2 \\
S_{xy} &= \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})
\end{align}

　式が導出できました。数字ばかりでよく分からないという人は、以下記事でイメージを理解できると思います。

Pythonを使った回帰分析の概念の解説その１

　ここまできたら、あとは$x$,$y$の共分散($S_{xy}$) と$x$の分散($S_{xx}$)を計算するだけです。

　pandasで読み込んだデータをNumpyのデータ形式に変換します。

　x, y と x, yを結合した行列を、それぞれ np_x, np_y, np_xy という Numpy の配列として読み込みます。

import numpy as np
np_x = x.values
np_x = np_x.T[0]
np_y = y.values
np_y = np_y.T[0]
np_xy = np.stack([np_x, np_y])

print('np_x:', np_x)
print('np_y:', np_y)
print('np_xy:')
print(np_xy)

　以下は実行結果です。

np_x: [ 1  2  5 10 28 40]
np_y: [ 1  2  5 10 28 40]
np_xy:
[[ 1  2  5 10 28 40]
 [ 2  3  2  3  4  6]]

　モデル関数の回帰係数 $w_1$は、先ほど求めたように以下となります。

\hat{w_1} = \frac{S_{xy}}{S_{xx}}

　まずは $x$の分散($S_{xx}$)と$x$,$y$の共分散($S_{xy}$)を求めていきます。

　Numpyのconvメソッドに$x$,$y$を結合した行列を引数で渡して返ってくる行列の[0][0]が$x$の分散、[0][1], [1][0]の要素が$x$,$y$の共分散, [1][1]の要素が$y$の分散になります。

s_xy = np.cov(np_xy, rowvar=1, bias=1)

print(s_xy)

　以下は実行結果です。

[[213.55555556  18.88888889]
 [ 18.88888889   1.88888889]]

　x,yの分散は np.var(np_x), np.var(np.y)でも求められます。同じ値になることを確認します。

s_xx = np.var(np_x)
s_yy = np.var(np_y)

print('S_xx : %.3f' %s_xx)
print('S_yy : %.3f' %s_yy)

以下は実行結果です。

S_xx : 213.556
S_yy : 1.889

　同じ値になっていますね。

　$S_{xx}$ $S_{yy}$が求まったので、回帰係数$\hat{w_1}$を計算します。ここでは、scikit-learnで計算した値と同じになることを確認します。

w_1 = s_xy[0][1] / s_xx
print('w1 : %.3f' %w_1)

以下は実行結果です。

w1 : 0.088

　$\hat{w_0}$を計算します。$\hat{w_0}$は先ほど求めた$\hat{w_1}$と$x$と$y$の平均値を使って求めることができます。

np_x_mean = np_x.mean()
np_y_mean = np_y.mean()

w_0 = np_y_mean - w_1 * np_x_mean
print('w0 : %.3f' %w_0)

以下は実行結果です。

w0 : 2.066

決定係数と相関係数

　単回帰モデルの決定係数$R$ を求めます。$R$が1に近いほど、$x$が$y$を説明できているということになるそうです。

　決定変数は、全変動($S_{all}$)、回帰変動($S_{reg}$), 残差変動($S_{res}$)から計算できます。$S_{all}$, $S_{reg}$, $S_{res}$, $R$には以下のような関係があります。

\begin{eqnarray}
S_{all} &=& S_{reg} + S_{res}\\
R &=& \frac{S_{reg}}{S_{all}}\\
\end{eqnarray}

　詳細は、以下サイトを参照下さい。ここでは、それぞれをNumpyで計算していきます。

　$S_{all}$の計算

s_all = ((y.values - y.values.mean())**2).sum()
print(s_all)

　計算結果は以下です。

11.333333333333334

$S_{reg}$の計算

s_reg = ((model_lr.predict(x.values) - y.values.mean())**2).sum()

print(s_reg)

　計算結果は以下です。

10.024280263614292

$S_{res}$の計算

s_res = ((y.values - model_lr.predict(x.values))**2).sum()
print(s_res)

　計算結果は以下です。

1.3090530697190428

　以下で、計算した$S_{all}$と$S_{reg}+S_{res}$が等しいことを確認します。

print('Sall: %.3f' %s_all)
print('Sreg + Sres: %.3f' %(s_reg + s_res))

　以下は実行結果です。

Sall: 11.333
Sreg + Sres: 11.333

　$R^2 = S_{reg}/S_{all}$ より $R^2$を計算

R2 = s_reg / s_all
print('R^2: %.3f' %R2)

　以下は実行結果です。

R^2: 0.884

　$S_{xx}$, $S_{yy}$, $S_{xy}$ から求められる相関係数$r$という値があるのですが、決定係数と相関係数の間には以下のような関係があります。

R^2 = r^2

詳細は以下リンク先参照下さい。

　ここではNumpyで$r$を求め、$R^2 = r^2$ となることを確認します。

r = s_xy[0][1] / (s_xx * s_yy)**(0.5)
r2 = r**2
print('r2: %.3f' %r2)
print('R^2: %.3f' %R2)

　以下は実行結果です。

r2: 0.884
R^2: 0.884

　相関係数は、Numpyのcorrcoefというメソッドを使っても計算できます。

np.corrcoef(np_xy)

　以下は実行結果です。

array([[1.        , 0.94047611],
       [0.94047611, 1.        ]])

[0][1]と[1][0]の要素が相関係数です。2乗して$R^2$と等しくなることを確認します。

np.corrcoef(np_xy)[0][1]**2

　以下は実行結果です。

0.8844953173777311

Scikit-learnで求めた値と同じになりましたね。

統計的な解釈

　次に、統計的な解釈を行います。ここは、statsmodelというライブラリを使って一気にやってしまいます。

import statsmodels.api as sm

x_add_const = sm.add_constant(x)
model_sm = sm.OLS(y, x_add_const).fit()
print(model_sm.summary())

　以下が実行結果です。

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.884
Model:                            OLS   Adj. R-squared:                  0.856
Method:                 Least Squares   F-statistic:                     30.63
Date:                Mon, 02 Sep 2019   Prob (F-statistic):            0.00521
Time:                        09:53:19   Log-Likelihood:                -3.9463
No. Observations:                   6   AIC:                             11.89
Df Residuals:                       4   BIC:                             11.48
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.0656      0.327      6.314      0.003       1.157       2.974
x              0.0884      0.016      5.534      0.005       0.044       0.133
==============================================================================
Omnibus:                          nan   Durbin-Watson:                   3.036
Prob(Omnibus):                    nan   Jarque-Bera (JB):                0.484
Skew:                           0.332   Prob(JB):                        0.785
Kurtosis:                       1.777   Cond. No.                         28.7
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

　今まで求めた、モデル関数の回帰係数 $w_1 = 0.088$, モデル関数の切片 $w_0 = 2.066$, 決定係数 $R^2 = 0.0884$に加え、今回生成した線形モデルに対する、様々な統計的な評価値が算出されています。

　検定とか、信頼区間と言われるようなものです。そうです、よく分かっていません。ごめんなさい。

　ざっくりとした見方としては、ここでは const が切片($w_0$)、 xが回帰係数($w_1$)を意味しています。

　それぞれの P>|t| は 0 に近いほど妥当性があるということになります。一般的には0.05 以下なら妥当性があるとするらしいです。今回は、0.003と0.005なので十分小さい値です。

　また、信頼区間は constが 1.157〜2.974、 xが0.044〜0.133となっていますが、これは推定値（yの値）がだいたい（95%以上）この範囲の中にデータが収まっているよという入力値（xの値）の範囲です。

他のデータセットでの確認

　今回は、私が独自に作ったデータを使って分析をしてみましたが、他のデータセットでの分析にも挑戦してみましょう。

　データ分析の例としてよく使われる、UC バークレー大学の UCI Machine Leaning Repository にて公開されている、「Wine Quality Data Set (ワインの品質)」の赤ワインのデータセットを使ってみましょう。

　データセットは、以下のコマンドでダウンロードできます。

!wget http://pythondatascience.plavox.info/wp-content/uploads/2016/07/winequality-red.csv

あとは、以下の通りにpandasでデータを読み込んで、x, yに入力すれば、この記事でやったことと同じ分析をすることが可能です。

import pandas as pd

df = pd.read_csv('winequality-red.csv', sep=';')
df.head()

x = df[['density']]
y = df[['alcohol']]

まとめ

　単回帰分析に関して学びました。次回は重回帰分析の予定です。

　文章への編集リクエスト、コードへのPull Requestお待ちしております。

次回：Pythonで基礎から機械学習「重回帰分析」

参考リンク

最小二乗法の導出

279

314

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで基礎から機械学習 「単回帰分析」

はじめに

単回帰分析

データの読み込みと可視化

scikit-learnを使った単回帰分析

Numpyを使った単回帰分析

決定係数と相関係数

統計的な解釈

他のデータセットでの確認

まとめ

参考リンク

最小二乗法の導出

Pythonで基礎から機械学習「単回帰分析」