【機械学習】最小二乗法について メモ

機械学習で使用することを前提として、最小二乗法についてまとめます。 ど文系のメモなので、誤りなどあったら指摘していただければ嬉しいです。

最小二乗法とは

最小二乗法(さいしょうにじょうほう、さいしょうじじょうほう；最小自乗法とも書く、英: least squares method)は、測定で得られた数値の組を、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差の二乗和を最小とするような係数を決定する方法、あるいはそのような方法によって近似を行うことである。(Wikipedia)

あるデータの分散について回帰を行いたいときなどに用いる考え方。
回帰直線をはじめとし、ロッソ回帰やリッジ回帰などの根底となる概念。

数式について

数式

モデル関数を f(x) とするとき

\sum_{i=1}^{n}{{(y_i-f(x))^2}} 

が最小となるように f(x) を求めることである

数式の意味

文字の意味	説明
f(x)	暫定的に分散空間上に引いた関数のこと。モデル関数
y	分散しているそれぞれのデータのこと。
yi-f(x)	分散しているそれぞれのデータと、分散空間上に引いた差のこと。
(yi-f(x))^2	上の式で求めた結果に絶対値による違いを取り除く処理を加えたもの。

分散空間上に関数の存在を仮定し、分散したデータそれぞれとの差を測定する。
その差が最も小さくなるように f(x) を設定できたならば、すなわちその関数は分散に対して最も相関性のある関数と言える。

プログラムによる実践

最小二乗法に基づいている直線回帰モデルを使用して、作成される関数のイメージを掴む。

直線回帰モデルによる最小二乗関数の可視化

import pandas as pd
import matplotlib.pyplot as pyp
from numpy.random import *
from sklearn.linear_model import LinearRegression

# x軸
data_x = pd.DataFrame([0,1,2,3,4,5,6,7,8,9])
# y軸　データはランダムに生成
data_y = pd.DataFrame(randn(10))

# 回帰直線モデルを生成
model_lr = LinearRegression()
# 最小二乗法に基づいて、モデル関数を作成
model_lr.fit(data_x, data_y)

pyp.plot(data_x, data_y, 'o')
pyp.plot(model_lr.predict(data_x), linestyle="solid")
pyp.show()

print('モデル関数の回帰変数 : %.3f' %model_lr.coef_)
print('モデル関数の切片 : %.3f' %model_lr.intercept_)

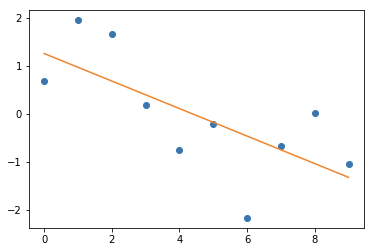
グラフ上の分散に対して最小二乗法を実行し、発見されたモデル関数を直線で表したのが上記の図。
ここでも求められた直線は
y = -0.287 * x + 1.261
となる。

以上。