はじめに
**回帰モデルの基本である線形回帰の理論について解説していきます。**特に以下の内容について説明します。サンプルデータを用いたPythonでの実装方法についてはこちらで解説の記事を書きました。
- 線形とは?(非線形との違い)
- 線形回帰モデルの概念(最小二乗法による係数の決め方やイメージ)
※機械学習やプログラミング関係の内容を他にも投稿していますので、よろしければこちらの一覧から他の投稿も見て頂けますと幸いです。
線形とは?
関数の線形・非線形を簡単にまとめますと以下の通りです。
- 線形関数:グラフが直線になる関数 (例)y=x, y=-3x
- 非線形関数:グラフが直線にならない関数 (例)y=x2, y=sinx
単回帰分析と重回帰分析とは?
少し脱線しますが、たまに聞く単回帰分析・重回帰分析について以下にまとめます。
- 単回帰分析は説明変数(x)が1つ、目的変数(y)が1つの回帰分析
→式で表すとy=ax+b
- 重回帰分析は説明変数(x)が2つ以上、目的変数(y)が1つの回帰分析
→式で表すとy=b0+b1x1+b2x2+…
xの前についている定数b1, b2…を「偏回帰係数」といいます
線形回帰とは?
説明変数をx、目的変数をyとした際に線形回帰モデルは以下のように表されます。εはノイズ(擾乱項)を表しますが、係数wを決定していく際には0と仮定して扱われます。
y = w_0+w_1x_1+w_2x_2+…+w_dx_d+ε
ここから係数wを決定して線形回帰モデルを決定します。以下にn個のデータがある際にwを決定する方法について簡単に説明していきます。
\boldsymbol{X}=
\begin{pmatrix}
1&x_{11}&x_{12}&\cdots&x_{1d} \\
1&x_{21}&x_{22}&\cdots&x_{2d} \\
\vdots & \vdots& \vdots&&\vdots& \\
1&x_{n1}&x_{n2}&\cdots&x_{nd} \\
\end{pmatrix}
\boldsymbol{w}=
\begin{pmatrix}
w_0 \\
w_1 \\
w_2 \\
\vdots \\
w_d
\end{pmatrix}
とすると、線形回帰モデルによる予測値は以下のように表すことができます。
\boldsymbol{\overline{y}}=\boldsymbol{Xw}
実際の目的変数(ターゲット)を**y**とすると、モデルの誤差の二乗和Eは以下のように表すことができます。
E=||\boldsymbol{y-Xw}||^2
Eを最小にするために勾配を計算して、その値を0とすると以下の式が得られます。
\boldsymbol{w}=\boldsymbol{(X^TX)^{-1}}X^Ty
ここからの解法は割愛させていただきますが、 こちらなどを参考にしていただければと思います。このように線形回帰モデルを決定していく手法を**「最小二乗法」**といい、係数決定の一般的な手法です。
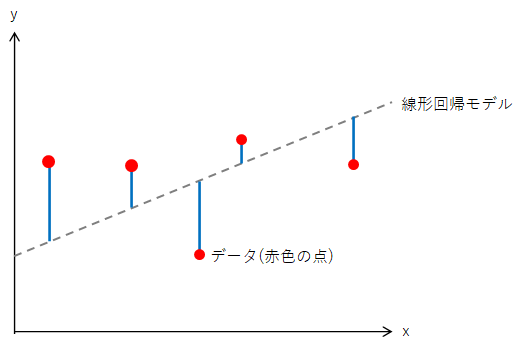
最小二乗法が何をしているか、以下の図を用いて説明します。青色の線の長さは線形回帰モデルと実際のデータ(赤色のプロット)との誤差を表しています。この誤差の二乗和が最小となるとき、線形回帰モデルはデータを最も精度よく予測できている状態になります。つまり、最小二乗法は青色の線の長さの総和を最小にして(最も精度の高い回帰モデルを作っている)のです。
まとめ
線形回帰の理論について解説いたしました。
- 線形回帰は説明変数と目的変数を線形関係(直線的な関係)で結びつけた回帰モデルである
- 線形回帰モデルの式は最小二乗法により決定される
pythonでの線形回帰の実装方法についてはこちらに投稿しています。