【RからPythonへ】ガウス平面上の単位円(Unit Circle)/単位円筒(Unit Cylinder)表示からの再出発

数年前、つまり2010年代後半「まだR**なんて使ってるの？　**Rが許されるのは2010年代前半までだよね。今はもうPythonの時代だよ!!」と煽られた事がありました。
キモーイガールズ (きもーいがーるず)とは【ピクシブ百科事典】

その時はティンダロスの猟犬(The Hounds of Tindalos)問題ことオイラーの公式（Eulerian Formula）e^Θi=cos(Θ)+sin(Θ)iの自明的な拡張であるCos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)を示して「大事なのは扱ってる中身だ」と宣言して何とか乗り切ったのですが…
【無限遠点を巡る数理】「ティンダロスの猟犬(The Hounds of Tindalos)問題」を世に解き放つ。

流石に2020年代ともなるとねぇ…コンピューターの世界における進歩はまさに非常なまでに日進月歩な訳です。ついていけなくなるとたちまち老害扱いという…

#Pythonにおける等差数列表現(Arithmetic Sequence Explession)
Pythonで等差数列を作る方法【初心者向け】
Pythonにおけるrepeat()の利用方法を現役エンジニアが解説【初心者向け】

import math as m
import numpy as np
a=range(0,10,1)
print(a)
b=np.arange(0,10,1)
print(b)
print(m.pi)
c=np.linspace(-m.pi,m.pi,61,endpoint = True)
print(c)
d=np.linspace(-m.pi,m.pi,61,endpoint = False)
print(d)
e=np.repeat(1,61)
print(e)

range(0, 10)
[0 1 2 3 4 5 6 7 8 9]
3.141592653589793
[-3.14159265 -3.0368729  -2.93215314 -2.82743339 -2.72271363 -2.61799388
 -2.51327412 -2.40855437 -2.30383461 -2.19911486 -2.0943951  -1.98967535
 -1.88495559 -1.78023584 -1.67551608 -1.57079633 -1.46607657 -1.36135682
 -1.25663706 -1.15191731 -1.04719755 -0.9424778  -0.83775804 -0.73303829
 -0.62831853 -0.52359878 -0.41887902 -0.31415927 -0.20943951 -0.10471976
  0.          0.10471976  0.20943951  0.31415927  0.41887902  0.52359878
  0.62831853  0.73303829  0.83775804  0.9424778   1.04719755  1.15191731
  1.25663706  1.36135682  1.46607657  1.57079633  1.67551608  1.78023584
  1.88495559  1.98967535  2.0943951   2.19911486  2.30383461  2.40855437
  2.51327412  2.61799388  2.72271363  2.82743339  2.93215314  3.0368729
  3.14159265]
[-3.14159265 -3.03858962 -2.93558658 -2.83258354 -2.7295805  -2.62657746
 -2.52357443 -2.42057139 -2.31756835 -2.21456531 -2.11156228 -2.00855924
 -1.9055562  -1.80255316 -1.69955012 -1.59654709 -1.49354405 -1.39054101
 -1.28753797 -1.18453493 -1.0815319  -0.97852886 -0.87552582 -0.77252278
 -0.66951975 -0.56651671 -0.46351367 -0.36051063 -0.25750759 -0.15450456
 -0.05150152  0.05150152  0.15450456  0.25750759  0.36051063  0.46351367
  0.56651671  0.66951975  0.77252278  0.87552582  0.97852886  1.0815319
  1.18453493  1.28753797  1.39054101  1.49354405  1.59654709  1.69955012
  1.80255316  1.9055562   2.00855924  2.11156228  2.21456531  2.31756835
  2.42057139  2.52357443  2.62657746  2.7295805   2.83258354  2.93558658
  3.03858962]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]

#Pythonにおける複素数表現(Complex Explession)
Python, complex型で複素数を扱う（絶対値、偏角、極座標変換など）
cmath --- 複素数のための数学関数

import math as m
import cmath as c
print(m.e)
print(m.log(2))
print(c.exp(1))
print(c.log(2))

2.718281828459045
0.6931471805599453
(2.718281828459045+0j)
(0.6931471805599453+0j)

ガウス平面(Gaussian Plane)=複素平面(Complex Plane)上の単位円(Unit circle)
Pythonで複素数扱うときに役立ちそうなことをまとめてみる

Rと異なり、ここからfor構文導入が必須となる？
Pythonのfor文によるループ処理（range, enumerate, zipなど）
Pythonの配列の基礎をご紹介！
数値の配列(リスト)を要素ごとに加算/減算/乗算/除算するには(ベクトル演算)

検証の為に比較演算子にも手を出しました。
比較演算子の使い方

import math as m
import cmath as c
import numpy as np

#絶対値と偏角リストから単位円を生成する。
#以下はエラーとなる。(まさかの1個ずつしか処理出来ないだと？)
a=np.linspace(-m.pi,m.pi,61,endpoint = True)
b=np.repeat(1,61)
print(c.rect(a,b))

TypeError: only size-1 arrays can be converted to Python scalars

#一応試してみた(当然そんな関数はない)。
print(np.rect(a,b))

AttributeError: module 'numpy' has no attribute 'rect'

#こうしないといけないって事?
ab=[]
for num in range(len(a)):
    ab.append(c.rect(a[num],b[num]))

print(len(ab))
print(ab)

61
[(-1.6974097548329732-2.643559064081456j), (-1.6408294296718742-2.555440428612074j), (-1.5842491045107752-2.4673217931426925j), (-1.527668779349676-2.3792031576733104j), (-1.4710884541885767-2.2910845222039287j), (-1.4145081290274777-2.202965886734547j), (-1.3579278038663787-2.114847251265165j), (-1.3013474787052797-2.026728615795783j), (-1.2447671535441804-1.9386099803264012j), (-1.1881868283830812-1.8504913448570193j), (-1.1316065032219824-1.7623727093876376j), (-1.0750261780608832-1.6742540739182556j), (-1.018445852899784-1.5861354384488737j), (-0.9618655277386848-1.4980168029794918j), (-0.9052852025775858-1.40989816751011j), (-0.8487048774164866-1.321779532040728j), (-0.7921245522553876-1.2336608965713463j), (-0.7355442270942885-1.1455422611019643j), (-0.6789639019331893-1.0574236256325824j), (-0.6223835767720902-0.9693049901632006j), (-0.5658032516109912-0.8811863546938188j), (-0.509222926449892-0.7930677192244369j), (-0.452642601288793-0.7049490837550552j), (-0.39606227612769385-0.6168304482856732j), (-0.33948195096659467-0.5287118128162912j), (-0.2829016258054957-0.4405931773469096j), (-0.2263213006443965-0.3524745418775276j), (-0.16974097548329733-0.2643559064081456j), (-0.11316065032219838-0.17623727093876398j), (-0.05658032516109919-0.08811863546938199j), 0j, (0.05658032516109895+0.08811863546938162j), (0.11316065032219813+0.17623727093876362j), (0.16974097548329733+0.2643559064081456j), (0.22632130064439626+0.35247454187752725j), (0.28290162580549544+0.4405931773469092j), (0.33948195096659467+0.5287118128162912j), (0.3960622761276936+0.6168304482856728j), (0.4526426012887928+0.7049490837550548j), (0.509222926449892+0.7930677192244369j), (0.5658032516109909+0.8811863546938185j), (0.6223835767720899+0.9693049901632j), (0.6789639019331893+1.0574236256325824j), (0.7355442270942882+1.145542261101964j), (0.7921245522553872+1.2336608965713456j), (0.8487048774164866+1.321779532040728j), (0.9052852025775856+1.4098981675101097j), (0.9618655277386845+1.4980168029794914j), (1.018445852899784+1.5861354384488737j), (1.075026178060883+1.6742540739182552j), (1.1316065032219818+1.762372709387637j), (1.1881868283830812+1.8504913448570193j), (1.2447671535441802+1.938609980326401j), (1.3013474787052792+2.0267286157957827j), (1.3579278038663787+2.114847251265165j), (1.4145081290274775+2.2029658867345465j), (1.4710884541885765+2.291084522203928j), (1.527668779349676+2.3792031576733104j), (1.584249104510775+2.467321793142692j), (1.6408294296718737+2.5554404286120738j), (1.6974097548329732+2.643559064081456j)]

#今度はオイラーの公式Cos(θ)+Sin(θ)i式で合成
#やはり同じエラーが出る。
complex(m.cos(a),m.sin(a))

TypeError: only length-1 arrays can be converted to Python scalars

#これもこうしないといけないって事？
ao=[]
for num in range(len(a)):
    ao.append(complex(m.cos(a[num]),m.sin(a[num])))

print(len(ao))
print(ao)

61
[(-1-1.2246467991473532e-16j), (-0.9945218953682733-0.10452846326765373j), (-0.9781476007338057-0.2079116908177593j), (-0.9510565162951535-0.3090169943749475j), (-0.9135454576426008-0.40673664307580043j), (-0.8660254037844387-0.49999999999999994j), (-0.8090169943749473-0.5877852522924732j), (-0.7431448254773944-0.669130606358858j), (-0.6691306063588582-0.7431448254773942j), (-0.587785252292473-0.8090169943749475j), (-0.5000000000000001-0.8660254037844386j), (-0.40673664307580026-0.9135454576426009j), (-0.30901699437494734-0.9510565162951536j), (-0.20791169081775934-0.9781476007338057j), (-0.10452846326765355-0.9945218953682733j), (6.123233995736766e-17-1j), (0.10452846326765344-0.9945218953682733j), (0.20791169081775923-0.9781476007338057j), (0.30901699437494745-0.9510565162951535j), (0.40673664307580015-0.9135454576426009j), (0.49999999999999994-0.8660254037844387j), (0.5877852522924732-0.8090169943749473j), (0.669130606358858-0.7431448254773944j), (0.7431448254773941-0.6691306063588583j), (0.8090169943749475-0.5877852522924731j), (0.8660254037844385-0.5000000000000002j), (0.9135454576426009-0.4067366430758003j), (0.9510565162951535-0.3090169943749474j), (0.9781476007338056-0.20791169081775962j), (0.9945218953682733-0.10452846326765361j), (1+0j), (0.9945218953682734+0.10452846326765318j), (0.9781476007338057+0.20791169081775918j), (0.9510565162951535+0.3090169943749474j), (0.913545457642601+0.40673664307579993j), (0.8660254037844387+0.49999999999999983j), (0.8090169943749475+0.5877852522924731j), (0.7431448254773945+0.669130606358858j), (0.6691306063588583+0.743144825477394j), (0.5877852522924732+0.8090169943749473j), (0.5000000000000003+0.8660254037844385j), (0.40673664307580076+0.9135454576426006j), (0.30901699437494745+0.9510565162951535j), (0.20791169081775968+0.9781476007338056j), (0.10452846326765411+0.9945218953682733j), (6.123233995736766e-17+1j), (-0.10452846326765312+0.9945218953682734j), (-0.2079116908177587+0.9781476007338058j), (-0.30901699437494734+0.9510565162951536j), (-0.4067366430757999+0.9135454576426011j), (-0.4999999999999994+0.866025403784439j), (-0.587785252292473+0.8090169943749475j), (-0.6691306063588579+0.7431448254773945j), (-0.7431448254773938+0.6691306063588587j), (-0.8090169943749473+0.5877852522924732j), (-0.8660254037844385+0.5000000000000003j), (-0.9135454576426006+0.4067366430758008j), (-0.9510565162951535+0.3090169943749475j), (-0.9781476007338056+0.20791169081775973j), (-0.9945218953682733+0.10452846326765418j), (-1+1.2246467991473532e-16j)]
#表示だけでなく内容も違う？
print(bool(ab==ao))

False
#ちなみにRみたいにベクトルの四則演算を実現したければnumpy.array()一択。
#しかし上掲のリスト処理がnumpy.array()には出来ない。
#つまり「変数の切り替え」が必要？

c=np.array(ab)
d=np.array(ao)

print(c+d)
print(c-d)
print(c*d)
print(c/d)

#計算結果省略。組み込みのリスト形式では+しか通らない。

これが全部最初からベクトル処理のRとライブラリ追加で追い上げたPythonの違い？…つまり偉いのはPythonというよりNumpyで、しかもその追いあげ方も演算効率優先(リスト操作の柔軟性が高く付くのはLISP時代からの問題点)という…
NumPy - Wikipedia
NumPyの歴史とPythonの並行処理(PyDataTokyo Conference)

1994年にPython1.0
1990年代にPILやNumPyの前身(Numeric) ←GitHubなどない暗黒時代

2001年くらいにEnthought（Anacondaと同種のプロダクト）：数値計算のコミュニティで盛り上がり

現在使われているものは2010年までには出揃っている（pandas, scikit-learn）

2010年代前半にAnaconda

なぜPythonが使われるようになったのか？
①NumPyが早い時期に誕生しエコシステムを形成
②PythonもNumPyを呼び出す前提で開発
③C拡張ライブラリの作りやすさ

2010年以降の機械学習ブームもあってPythonの人気が上昇
StackOverflowの記事数10%を占めるように（JSを抜いた）
python.jpもアクセス数3倍

「現実は常に正解である(by 立川談志)」?　まぁネイピアが「常用対数表(Common Log Table)」作成を思い立ってからこのかた、コンピューター言語は何よりもまず演算の為にあり続けてきた訳で「開発効率も演算効率も高いのは絶対正義」なのは否定出来ないんですよね。
「よく覚えとけ。現実は正解なんだ。」立川談志49歳のことばが身にしみる
【数理考古学】常用対数表(Table of Common Logarithms)を使った計算

#Pythonにおけるグラフ表現

Pythonでデータをプロットしてグラフを描く方法【初心者向け】

Rの場合と異なり、そのまま複素数リストを渡しても虚数部が切り捨てられてしまいます。

import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt

c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
ao=[]
for num in range(len(c0)):
    ao.append(complex(m.cos(c0[num]),m.sin(c0[num])))
plt.plot(ao);

#エラー表示
ComplexWarning: Casting complex values to real discards the imaginary part
return array(a, dtype, copy=False, order=order)

実数部と虚数部を切り離してx値/y値として渡してやると…今度はアスペクト比の調整段階で問題が生じました。しかしまぁこれまでの投稿で散々使い倒してきたRのplot関数の利用範囲に大分追いついてきた感じがします。
set_aspect() を用いて等軸の正方形のプロットを作成する
matplotlibのstyleを変える
Fill 塗りつぶし
matplotlib で指定可能な色の名前と一覧
Matplotlib で水平線と垂直線をプロットする方法
【Python@matplotlib】matplotlib にて横、縦の補助線を描く方法について

import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt

#単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)

#グラフ表示
plt.style.use('default')

fig = plt.figure()

plt.plot(s1.real,s1.imag,color="blue", label="Unit Circle")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Unit Circle")
plt.xlabel("Real")
plt.ylabel("Imaginal")
plt.fill(s1.real, s1.imag,color="gainsboro")

ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
ax.legend(loc='upper right')

#補助線
plt.axvline(0, 0, 1,color="red")
plt.axhline(0, 0, 1,color="red")

plt.show()

#エラー表示
MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance.  In a future version, a new instance will always be created and returned.  Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.
  ax = fig.add_subplot(111)

それでは今度は単位円(Unit Circle)の概念を単位円筒(Unit Cylinder)のに拡張してみましょう。そう、実は以前からこの処理内容がシームレスに連続していく感じは羨ましかった!!
Pythonで3D散布図を作成する方法を現役エンジニアが解説【初心者向け】

import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
z0=np.linspace(-1,1,61,endpoint = True)

#グラフ表示
plt.style.use('default')

fig = plt.figure()
ax = Axes3D(fig)

ax.plot(s1.real,s1.imag,z0,color="blue")
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Circle")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")

これもどうやらPythonが偉いというよりmatplotlibが偉いという話になってくる様です。しかし、とにかく常に現実は正解という…
matplotlib - Wikipedia

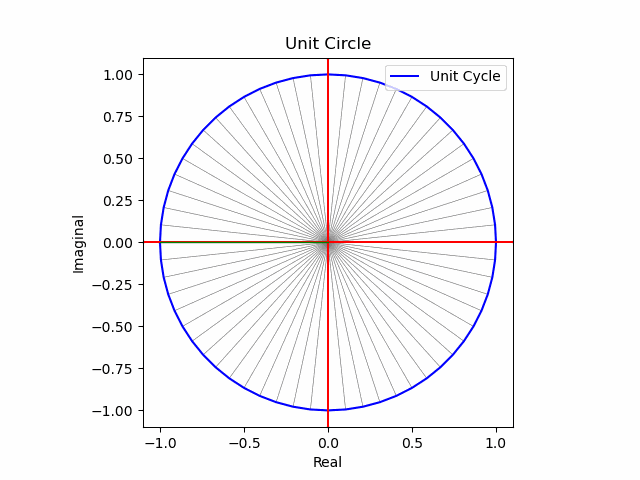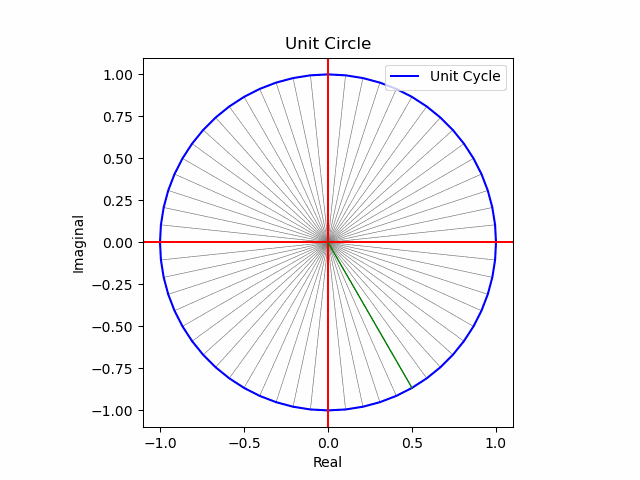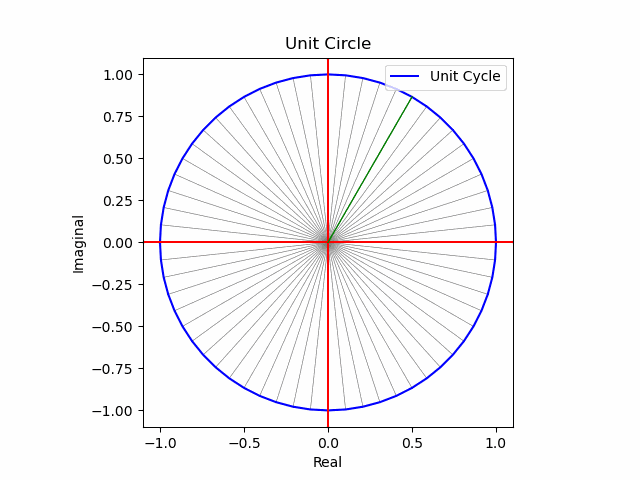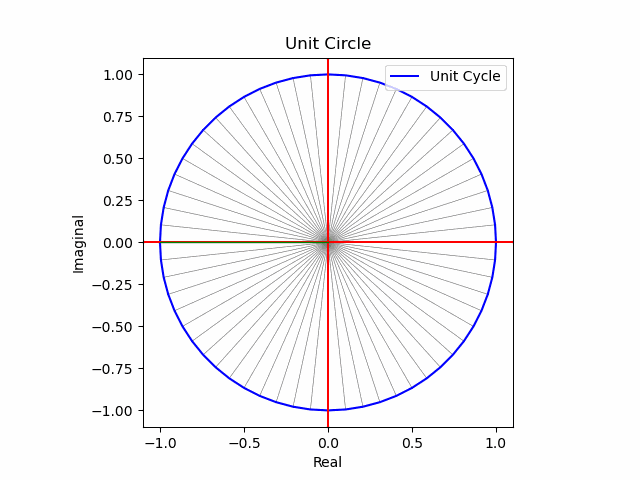
ついでに上掲のティンダロスの猟犬で用いた「スポーク表示」。どうやらRのplot関数とは異なりmatplotlibにはsegments関数の概念がなく「2点間plt.plot(ax.plot)」で間に合わせる模様。
Python: matplotlibで"任意の線"を引く
Adding an arbitrary line to a matplotlib plot in ipython notebook

2次元

import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt

#単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)

#グラフ表示
plt.style.use('default')
fig = plt.figure()

for num in range(len(s1)):
    plt.plot([0,s1[num].real],[0,s1[num].imag],color="gray",lw=0.5);

plt.plot(s1.real,s1.imag,color="blue", label="Unit Cylinder")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Unit Circle")
plt.xlabel("Real")
plt.ylabel("Imaginal")

ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
ax.legend(loc='upper right')

#補助線
plt.axvline(0, 0, 1,color="red")
plt.axhline(0, 0, 1,color="red")

plt.show()

3次元

import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
z0=np.linspace(-1,1,61,endpoint = True)

#グラフ表示
plt.style.use('default')

fig = plt.figure()
ax = Axes3D(fig)

#スポーク描画
ax.plot([0,0],[0,0],[-1,1],color="red",lw=1)
ax.plot([0,-1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,-1],[0,0],[1,1],color="red",lw=1)
for num in range(len(s1)):
    ax.plot([0,s1[num].real],[0,s1[num].imag],[z0[num],z0[num]],color="gray",lw=0.5);

ax.plot(s1.real,s1.imag,z0,color="blue")
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")

単位円筒(Unit Cylinder)とは要するに複素関数における分枝切断(Branch Cut)の構成単位だった訳ですね。これを連続させると、いわゆるリーマン面(Riemann Surface)になる訳です。
【無限遠点を巡る数理】等差数列と等比数列②基底関数概念の導入
複素解析での分岐点とは

複素解析の歴史の中で日本が関わってくるのは20世紀に入ってからである．
例えば日本語で書かれた最初の複素関数論のテキストは吉川實夫による『函数論』で，
1913年(大正二年)のことである．テキストでは複素関数は複函数と訳されていた．

このように訳語の問題が表れる．訳語は単純な思い違いが末代まで残ったり，細かな違いを反映させた語が選ばれても，時代の流れでより簡便な言い回しに喰われることもある．度が過ぎるとカタカナ表記という万能な手段が講じられてしまう．

複素解析で一二を争う特殊な訳語は「截線」という訳語ではないだろうか．

分岐や葉はbranchやleafなので，すんなり翻訳された感があるが，branch cutは分岐截線となった．今では単に切断とよぶことも多い．もしくはブランチカットと表記することもある．どちらにしても「截線」と訳すのはちょっと凝っているわけである．

「截(セツ)」という漢字は難しい漢字である．「載」「裁」と似ているし，「截線」を「せっせん」として漢字変換してくれなくても仕方がないほどである．この漢字の訓読みは「截る(きる)」「截つ(たつ)」で刃物で重なりのあるものや長いものをずばりと切る様をいうものである．斬釘截鉄 (ざんていせってつ) という四字熟語もあるが，これからとにかく切ればいいというわけではなく，重要な箇所を切るという意味もあり，遮るといった意味も持っている．

多価関数はまるで複素平面が何枚も折り重なったようなところを定義域とするようなものになっている．これら複素平面 (葉) が共有する部分で切るという様が截ち切るようになっているので，截線というわけである．
また複素平面のどこを切ってもよいわけでもなく，分岐点を端点に持つように切らねばならず，その意味でも截線という訳語の意図が込められているのではとも感じられる．

ところで「截線」は今の分岐截線の他に，曲線の二点以上と交点を持つ直線である割線(secant)の訳語としても用いられることがある．何れにしても今ではもう多くの人々が忘れた用語なのかもしれない．

次いで塗り潰しに挑戦したものの、とりあえず挫折。どうやらPoly3DCollection(四角ポリゴン (patch) の集合)の概念習得が必要な模様。
mplot3d.Axes3D – 3次元グラフの概要
matplotlib - plot_surface で 3D グラフを描画する方法
[matplotlib 3D] 11. 3Dグラフ上に円、線、面などの図形を表示(pathpatch3d)

ついでに条件文の構文についても触れる展開に。
Pythonのif文による条件分岐の書き方
Pythonの三項演算子（条件演算子）でif文を一行で書く

#Pythonにおけるアニメーション表現
何と最終的にはRでは実現困難な3Dアニメーションにまで到達してしまいました。そう、以前の投稿を見れば分かりますがR+OpenGLの組み合わせだと3次元立体は回転させる事しか出来なかったのですね(方法はあったのかもしれないが、そこまで到達出来なかった)。

matplotlib でアニメーションを作る
とほほのPython入門 - 関数
matplotlibでアニメーション
matplotlib.animationで動くグラフに挑戦！
matplotlibでimagemagickを使わずにアニメGIFを保存する

二次元

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
plt.style.use('default')
fig = plt.figure()

#関数定義
def unit_circle(n):
    plt.cla()
    #スポーク線描画
    for num in range(len(s1)):
        plt.plot([0,s1[num].real],[0,s1[num].imag],color="gray",lw=0.5);    
    #円周描画
    plt.plot(s1.real,s1.imag,color="blue", label="Unit Cylinder")
    plt.ylim([-1.1,1.1])
    plt.xlim([-1.1,1.1])
    plt.title("Unit Circle")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot(111)
    ax.set_aspect('equal', adjustable='box')
    ax.legend(loc='upper right')
    #補助線描画
    plt.axvline(0, 0, 1,color="red")
    plt.axhline(0, 0, 1,color="red")
    #移動線描画
    plt.plot([0,s1[n].real],[0,s1[n].imag],color="green",lw=1)

ani = animation.FuncAnimation(fig, unit_circle, interval=50,frames=len(s1))
ani.save("desktop/output02.gif", writer="pillow")

三次元

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
z0=np.linspace(-1,1,61,endpoint = True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #スポーク線描画
    ax.plot([0,0],[0,0],[-1,1],color="red",lw=1)
    ax.plot([0,-1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,-1],[0,0],[1,1],color="red",lw=1)
    for num in range(len(s1)):
        ax.plot([0,s1[num].real],[0,s1[num].imag],[z0[num],z0[num]],color="gray",lw=0.5);    
    ax.plot(s1.real,s1.imag,z0,color="blue")
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    #動線描画
    ax.plot([0,s1[n].real],[0,s1[n].imag],[z0[n],z0[n]],color="green",lw=1);

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(s1))
ani.save("desktop/output06.gif", writer="pillow")

こうして、これまでの投稿内容のPythonへの移植の目処が立ち始めた辺りで、以下続報…