我々の自然な時空間認識(Natural Space-Time Recognition)を、数理(Mathematical Things)が前提(Assumption)とする「直交座標系(Orthogonal System)=観察(Observation)とその評価結果(Evaluation)を互いに直交(Orthogonal)するN次元評価軸(N-Dimensional Evaluation Axis)上に配置(Layout)可能な機構(System)」に拡張するには、無限遠点(Inf(inity))の概念(Concept)からの再出発を必要とします。
脳と時空間のつながり vol.1 理化学研究所 脳神経科学研究センター(理研CBS)
assumptionの意味・使い方・読み方 | Weblio英和辞書
最も原始的な観測環境(Most Primitive Observation Environment)と、それへの単位元(Identity Element)概念の導入
まずは最も原始的な観測環境(Most Primitive Observation Environment)としてN次元評価軸(N-Dimensional Evaluation Axis)を有する観測原点(Observation Origin)Xn(n=1→Inf){0,0,0,…,0}と観測対象(Observation Target)の極限(Limit)たる無限遠点(Inf(inity))Yn(n=1→Inf){Inf,Inf,Inf,…,Inf}の2点を置き、両者を最短距離で結ぶ観測線(Observation Line)を設定します。
-
観測線とはいえ、実際の見え方としてはある種の極座標系(Polar Coordinate System)、すなわち一端がを観測原点に固定され、もう一端が無限長(Unlimited Length)の無限次元(Unlimited Dimensions)に発散(Convergence)/収束(Divergence)する同心円(Concentric Circles)/同心球面(Concentric Sphere)と映る。ただしこの段階ではあくまで単層。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
- そう、この距離が{0,Inf}間しか存在せず、半径(Radius)が観測距離無限(Unlimited Observation Length)/観測次元数無限(Unlimited Observation Dimensions)の無限円(Infinity Circle)/無限球面(Infinity Sphere)のみが存在する空虚な状態こそが、あらゆる観測環境(Observation Environment)の原風景といえよう。要するに「視野内に何もない宇宙空間を漂流する宇宙飛行士の視界」である。
【無限遠点を巡る数理】「無限遠点への発散」=「無限遠点への収束」? - 我々はこの状態より先に進む為、2次元空間と3次元空間を扱う事に特化したある種の「(カンブリア爆発期以降、一部の生物が視覚とそれに呼応する脊髄と運動機関のフィードバック体系を獲得する過程で依存する様になった)原始デカルト座標系 (Primitive Cartesian Coordinate System)」を利用してきた。実際、人類が純粋に数理上の演繹だけで「過去・現在・未来を有する前後左右上下のある空間」を相応の範囲で規定可能となったのはごく最近の出来事に過ぎない。
【無限遠点を巡る数理】「ピタゴラスの定理」と「デカルト座標系」の狭間
そしてここでいう原始デカルト座標系 (Primitive Cartesian Coordinate System)から離れる為の最初の一歩が、単位元(Identity Element)の概念(Concept)の導入(Introduction)となる訳です。
単位元 - Wikipedia
「距離1と次元数1の抽出→再帰演算処理による2以降/0以下の数字の補完と数直線の構成」によって到達する自然数、整数、有理数の定義。そして観測値分断問題(The Probrem of Division of Observation Line)の始まり。
単位元(Identity Element)の概念から出発すれば、新たな観測尺度(Observation Scale)として等差数列(Arithmetic Sequence=算術数列)Xn(n=-Inf→-1→0→1→Inf){-Inf,…,-1,0,1,…,Inf}や等比数列(Geometric Sequence=幾何数列)Xn(n=-Inf→0→→Inf){1/Inf,…,Inf/Inf,…,Inf/1}の概念を得る事が出来ます。
- 特定の次元について無限遠点(Infinity)/無限遠点(Infinity)=1を乗法単位元(Multiplicative Identity)と置くと、加法単位元(Additive Identity)0=1/無限遠点(Infinity)と無限遠点そのもの(Infinity Itself)=無限遠点(Infinity)/1は互いに逆数(Reciprocal)の関係にあると定義される。
- この様にある数xに逆数(Reciprocal)1/xを掛けた数が乗法単位元(Multiplicative Identity)1である様に、ある数に足すと加法単位元(Additive Identity)0となる数が反数(Opposite)であり、乗法単位元(Multiplicative Identity)1の場合それは符号を逆転させた-1となる。
群論(Group Theory)でいうところの加法群(Additive Group)と乗法群(Multiplicative Group)の関係性の大源流?
これから群論を学ぶ方のための入門講座
[群について基本的なこと:物理のかぎしっぽ]
(http://hooktail.sub.jp/algebra/GroupBasic/)
「加法群・乗法群」って? - Togetter
- 形而上学者(Metaphysicist)は1なる数字を神聖視していたが、実際「距離1と次元数1の抽出→再帰演算処理による2以降/0以下の数字の補完と数直線の構成」こそが最も原始的な観測環境(Most Primitive Observation Environment)から脱却する為の第一歩たる数直線(Number Line)構築の前提なので、その考え方自体は当たらずとも遠からずだったといえる。ただし、そうやって原始デカルト座標系 (Primitive Cartesian Coordinate System)の祝福/呪縛から解放された数理(Mathematical Things)の世界は、以降次第に(彼らが想像だに出来なかった)真の姿を取り戻していく展開を迎える。
とにかく、これでやっと自然数(Natural Number)Nと整数(Integer Number)Zなどの定義が導入(Introduction)可能となりました。
【初心者向け】集合論②「数直線の連続性」を巡る自然数/整数と有理数の定義上の断絶について
- 自然数(Natural Number)Nの定義…等差数列(Arithmetic Sequence)Nn(n=1→Inf(inity)){1=1,2=1+1,3=1+(1+1),4=1+(1+(1+1))…,Inf}の形で表される。加法単位元(Additive Identity)0と乗法単位元(Multiplicative Identity)1の距離(Distance)1から出発。
- 加法群(Additive Group)でもある整数(Integer Number)Zの定義…等差数列(Arithmetic Sequence)Zn(n=Inf→-1→0→1→-Inf){1=1,0=1-1,-1=1-(1+1),-2=1-((1+1)+1),…,Inf}の形で表される。上掲の自然数列に加法単位元(Additive Identity)0を中心として反数(Opposite)-1を掛けた等差数列(Arithmetic Sequence)Zn(n=1→-Inf){1=1,0=1-1,-1=1-(1+1),-2=1-((1+1)+1),…,Inf}を合成した結果。
-
乗法群(Multiplicative Group)でもある、単一元のみで構成される(要するにabやa/bといった形でない)有理数(Rational number)の定義…Qn(n=-Inf,…,-3,-2,-1,0,1,2,3,…,Inf){1/Inf=0,…,1/x^3,1/x^2,1/x,1,x,x^2,x^3,…,Inf}の形で表される。乗法単位元(Multiplicative Identity)1を中心に正の整数を添字とする等比数列(Geometric Sequence)Qn(n=0,1,2,3,…,Inf){1,x^1=x,x^2=xx,x^3=xxx,…,x^Inf=Inf}と負の整数を添字とする等比数列(Geometric Sequence)Qn(n=0,-1,-2,-3,…,-Inf){1,1/x^1=1/x,1/x^2,1/x^3,…,1/x^Inf=1/Inf=0}を合成したもの。その公比(Common Ratio)次第で複雑な収束の仕方をする事でも知られる。
等比数列(幾何数列)①その基本的性質について。
等比数列(幾何数列)②同心円集合に射影する準備
等比数列(幾何数列)③振動関数を巡る収束と拡散。
等比数列(幾何数列)④公比Dが正の場合の収束と拡散, そして対数尺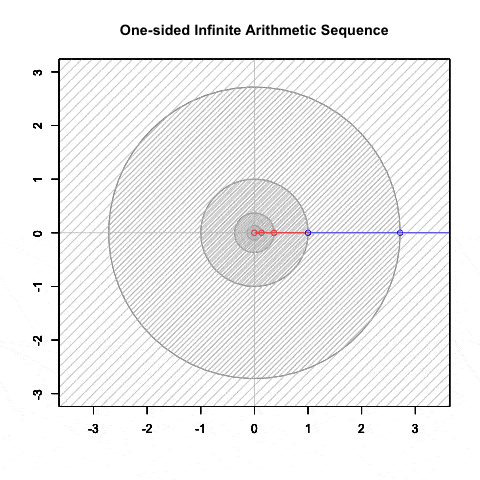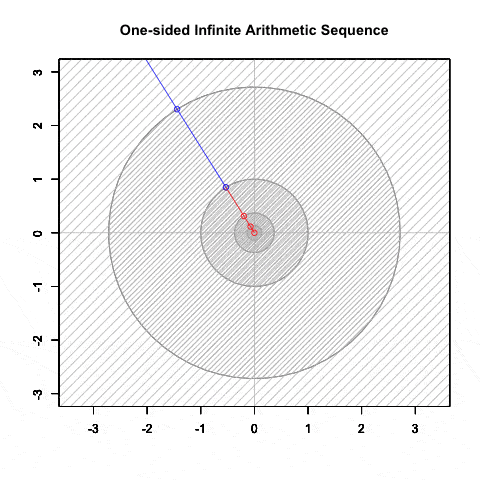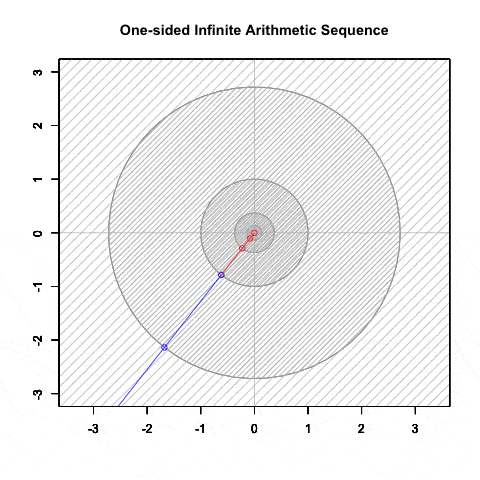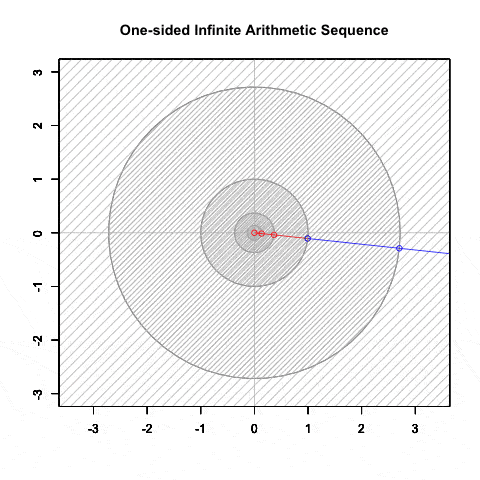
こうした純粋に数理(Mathematical Things)、すなわち「距離1と次元数1の抽出→再帰演算処理による2以降/0以下の数字の補完と数直線の構成」から出発する定義の成立が、同時に無限遠点(Inf(inity))に到達不可能となる「観測値分断問題(The Probrem of Division of Observation Line)」の始まりを意味したりするからややこしいのです。
【無限遠点を巡る数理】観測距離無限状態と観測次元数無限状態がもたらす「観測値分断問題」について。
そして改めて浮上してくる「半径の2倍は直径でOK?」問題。
ところでここでいう(自然数や整数の構成する)等差数列と(有理数が構成する)等比数列の境界線はそれほどはっきりしたものもありません。何しろ以下の様にも表記出来てしまうのです。
- 1=1^n(乗法単位元でもあるので何乗しても1は1のまま)
- 1+1=1*2=2^1=2
- (1+1)+(1+1)=2*2=2^2=4
- ((1+1)+(1+1))+((1+1)+(1+1))=222=2^3=8
その一方で(演算上、その出現順序に大きな意味がある)反数を用いた減算や、逆数を用いた除算により複数の「距離1と次元数1の抽出→再帰演算処理による2以降/0以下の数字の補完と数直線の構成」を合成すると、それだけでもう結合則(Associative law)(a○b)○c=a○(b○c)や交換則(Commutative Law)a○b=b○aや分配法則(Distributive property)a×(b○c)=(a×b)○(a×c),a/(b○c)=(a/b)○(a/c),(a○b)×c=(a×c)○(b×c),(a○b)/c=(a/c)○(b/c)に綻びが生じてしまう問題も浮上してきます。
交換法則、結合法則、分配法則
交換法則 - Wikipedia
結合法則 - Wikipedia
分配法則 - Wikipedia
ここで興味深いのが無限遠点(Inf(inity))と交換則(Commutative Law)の関係。
- Inf+a=a+Inf=Inf(交換則が成立)
- Inf-a=Inf, a-Inf=-Inf(交換則が成立しない)
- Infa=aInf=Inf(交換則が成立)
- Inf/a=Inf, a/Inf=0(交換則が成立しない)
ちなみに応用でこうも考えられます。
- Inf-Inf=0(加法単位元)
- Inf/Inf=1(乗法単位元)
あれ、もしかして、この話とも重なってくる部分が?
【無限遠点を巡る数理】「ピタゴラスの定理」と「デカルト座標系」の狭間
半径(Raduus)が構成するのは片側無限算術数列(One-Sided Infinite Sequence)
「自然数の世界」に該当

直径(Diameter)が構成するのは両側無限算術数列(both-Sided Infinite Sequence)。
「整数の世界」に該当
直線x=0を軸線に選んだ場合
(xの値の推移は-1から+1に及ぶが、Yの値は0以下/0以上に留まる)。
直線y=0を軸線に選んだ場合
(yの値の推移は-1から+1に及ぶが、xの値は0以下/0以上に留まる)。
そうは言っても「距離1と次元数1の抽出→再帰演算処理による2以降/0以下の数字の補完と数直線の構成」の最初の成果たる「片側数列」自然数から出発して「群としての体裁を整える=両側数列に拡張する」為にはこれらの演算を駆使せざるを得ず、まさにそのプロセスこそが以下の様な「直径の検出=円弧/球表面上の対蹠間を結ぶ立体幾何学の開始」と結びついているのです。
…
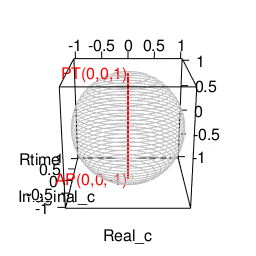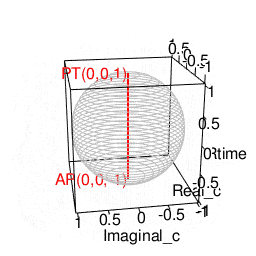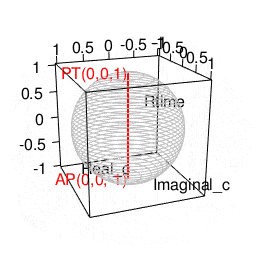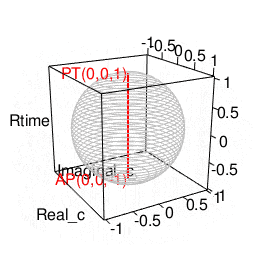
- 「円上において対蹠と任意の1点を1回だけ直角に曲がって結ぶ経路」や「球表面上において任意の2点を2回だけ直角に曲がって結ぶ経路」に注目する「ハミルトンの四元数(Hamilton's Quaternion)」の世界
ハミルトンの四元数(Hamilton's Quaternion)は何を表しているのか?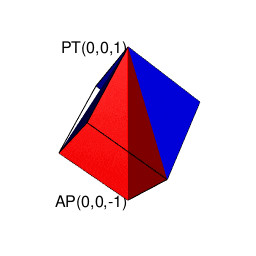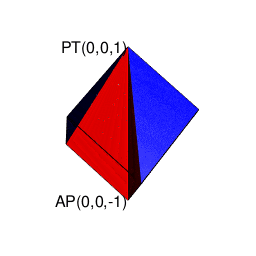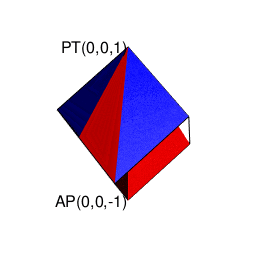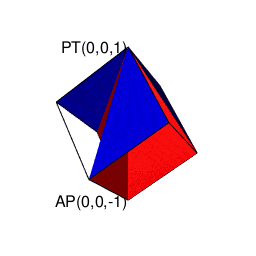
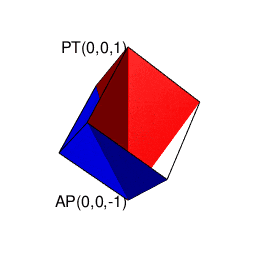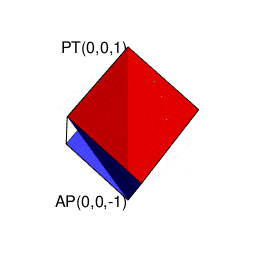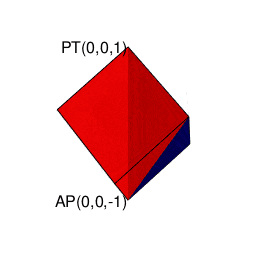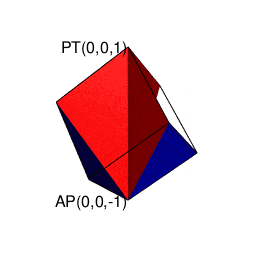
-
オイラーの多面体定理(Euler's Polyhedral Theorem)V(Vertexes=頂点数)-E(Edges=辺数)+F(Faces=面数)=2(Antipodes=対蹠数)に従って対蹠間を結ぶさらに複雑な経路を求める多面体幾何学の世界。ただしこれに含まれる「超八面体(Super Octahedron)=立方体を対角線に沿って直角に交差させ正八面体(Regular Octahedron)を生じさせる操作を無限に再帰的に繰り返す結果生まれる図形」といった諸概念は上掲の演算の延長線上に現れる(距離{0,1,Inf}の0から1にかけて成立)。
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…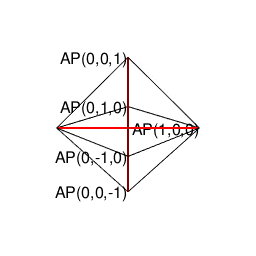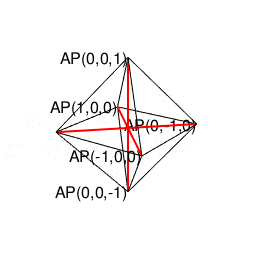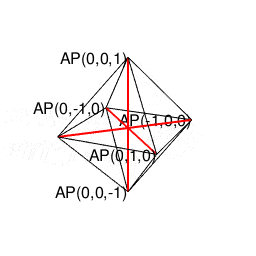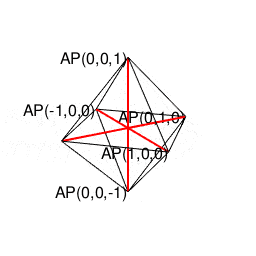
こうして全体像の俯瞰がやっと可能になった辺りで、以下続報…