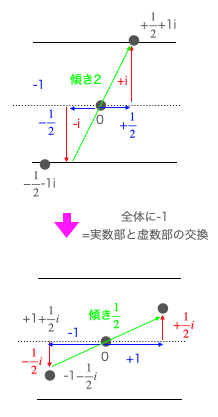
以前の投稿では、与えられた2点の相加平均(Arithmetic Mean)$\frac{a+b}{2}$と相乗平均(Geometric mean)$\sqrt{ab}$を求め複素円筒座標系を始める方法を試みました。
【Token】物理学と数学の接点について。
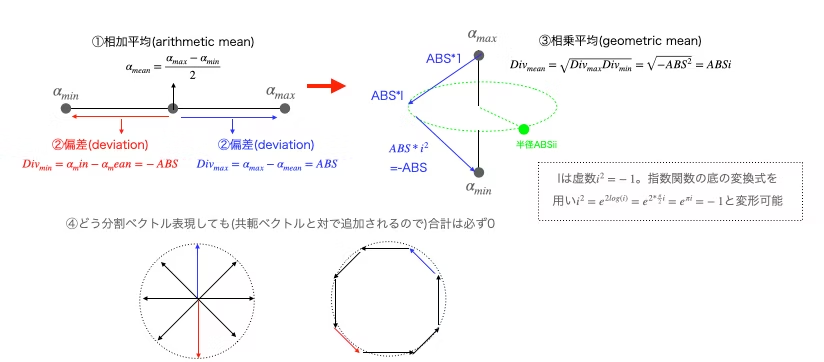

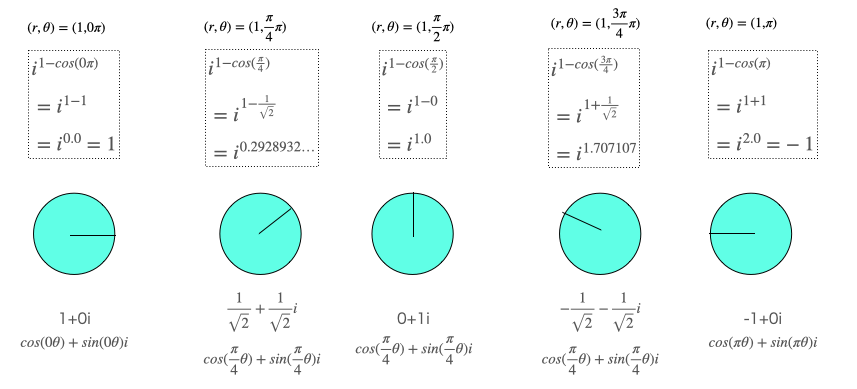
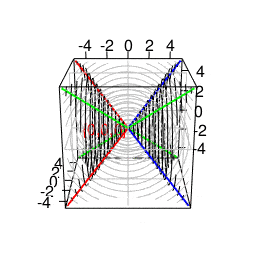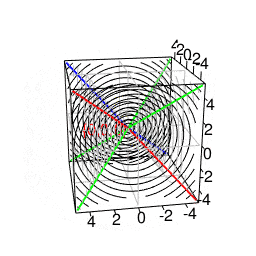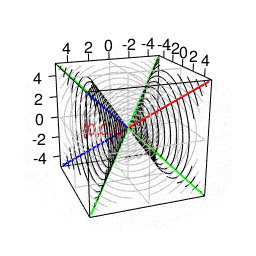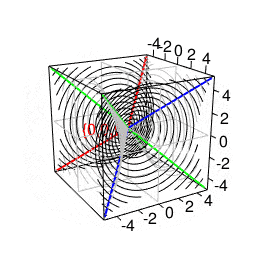
この複素円筒座標系$±i^{1-cos(θ)}(0≦θ≦π)$は、以下の様な考え方を導入する事により角度の概念も扱う事が出来ます。
複素円筒座標系における相関係数と線形回帰
ここで得られた偏差(-1+1i,+1+1i)にまつわる統計データをさらに集めてみましょう。
行列演算の基本④大源流における記述統計学との密接な関連性?
実数部平均$\bar{R}$も虚数部平均$\bar{I}$も0として、標本分散(Sample Variance)$S_R^2,S_I^2$と標本共分散(Sample Covariance)$S_{RI}$について…
S_R^2=\frac{\sum_{n=1}^{2}(Ri-\bar{R})^2}{n}=\frac{(-1)^2+(+1)^2}{2}=\frac{2}{2}=1
S_I^2=\frac{\sum_{n=1}^{2}(Ii-\bar{I})^2}{n}=\frac{(-1)^2+(+1)^2}{2}=\frac{2}{2}=1
S_{RI}=\frac{\sum_{n=1}^{2}(Ii-\bar{I})(Ri-\bar{R})}{n}=\frac{(-1)(-1)+(+1)(+1)}{2}=\frac{2}{2}=1
不偏分散(Unbiased Dispersion)$s_R^2,s_I^2$おと不偏共分散(Unbiased
Covariance)$s_{RI}$は…
s_R^2=\frac{\sum_{n=1}^{2}(Ri-\bar{R})^2}{n-1}=\frac{(-1)^2+(+1)^2}{2-1}=\frac{2}{1}=2
s_I^2=\frac{\sum_{n=1}^{2}(Ii-\bar{I})^2}{n-1}=\frac{(-1)^2+(+1)^2}{2-1}=\frac{2}{1}=2
s_{RI}=\frac{\sum_{n=1}^{2}(Ii-\bar{I})(Ri-\bar{R})}{n-1}=\frac{(-1)(-1)+(+1)(+1)}{2-1}=\frac{2}{1}=2
概ねサンプル数3000以上でその差を意識する必要がなくなるとされている標本分散と不偏分散ですが、データ数2の時にはこんな風に「単位円の半径1と直径2」くらい激烈な現れ方をするのですね。
【初心者向け】標本分散と不偏分散
それでは相関係数(Correlation Coefficient)rを求めてみましょう。
どうして相関係数の記号はrなのか?
まずは標本分散で計算した場合…
r=\frac{S_{IR}}{\sqrt{S_R^2}\sqrt{S_I^2}}=\frac{1}{\sqrt{1}\sqrt{1}}=\frac{1}{1}=1
次いで不偏分散で計算した場合…
r=\frac{s_{RI}}{\sqrt{s_R^2}\sqrt{s_I^2}}=\frac{2}{\sqrt{2}\sqrt{2}}=\frac{2}{2}=1
今度は線型方程式$y=a_Rx+b_R,x=a_Iy+b_I$の、切片$b_R,b_I$は共に0として傾き$a_R,a_I$を求めてみます。標本共分散で計算した場合…
a_R=\frac{S_{RI}}{S_R^2}=\frac{1}{1}=1
a_I=\frac{S_{RI}}{S_I^2}=\frac{1}{1}=1
不偏共分散で計算した場合…
a_R=\frac{s_{RI}}{s_R^2}=\frac{2}{2}=1
a_I=\frac{s_{RI}}{s_I^2}=\frac{2}{2}=1
どちらの計算でも分子と分母で打ち消し合うので特に違いは現れません。これくらいデータが単純だと「相関係数1,線型方程式y=ax+bのa=1,b=0」は計算するまでもなく丸わかりですが、あえて計算するとこういう感じになるという話…
複素円錐座標系における相関係数と線形回帰
今度は二項の実数部と虚数部の符号を互い違いにしてみましょう。
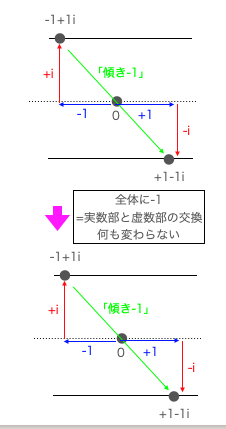
これは円錐座標系上における半回転に該当します。
【Token】反比例関数と指数対数関数の回転



- なお相関係数は「二つの円筒座標系を直交させ(仮にx軸,y軸と呼ぶ)、そこに現れる楕円断面の回転を第三の直交軸から観察する場合の射影」とも規定出来たりする。この場合、z軸とy軸の直交を前提に回転するX軸は①断面が線型に観察される時はz軸と直交。②真円状に観察される時はz軸とぴったり重なり合っている。

- その一方で、かかる楕円と円錐の接線から垂直に伸ばされた軌跡は「円錐曲線の数理」に従って放物線を描く。
【Token】円錐座標系
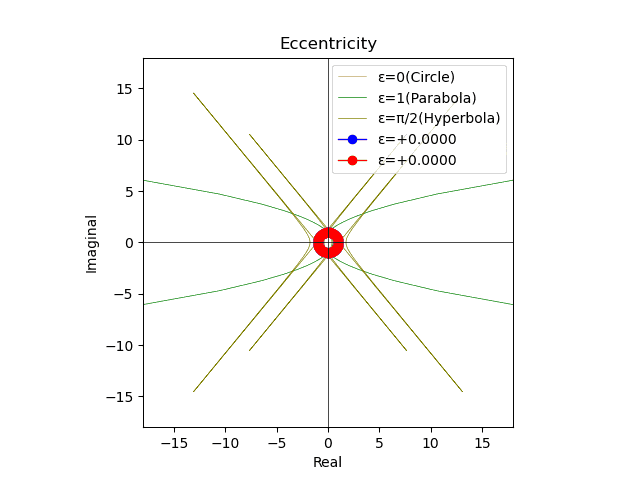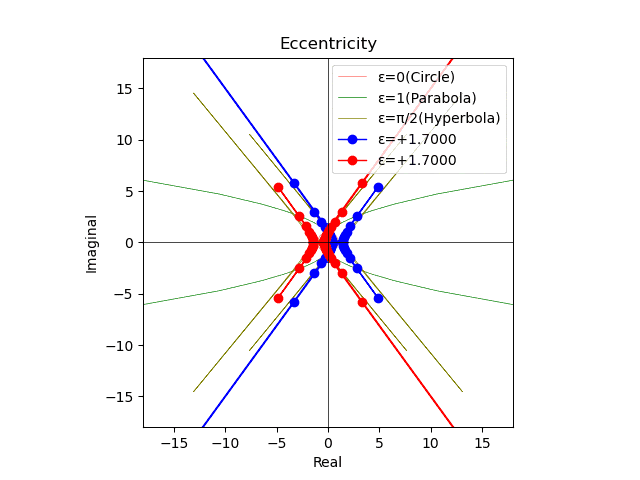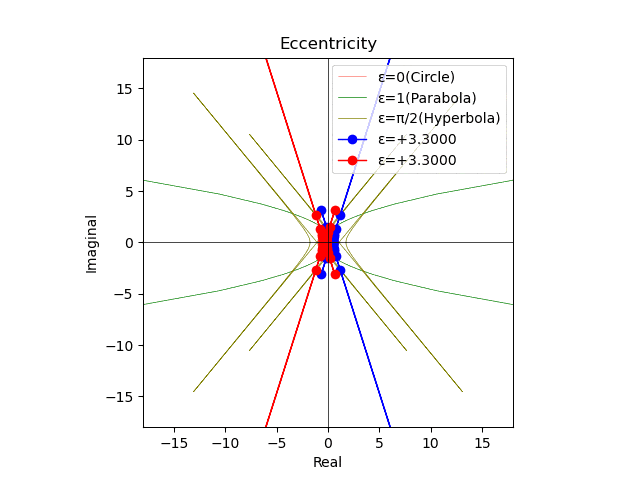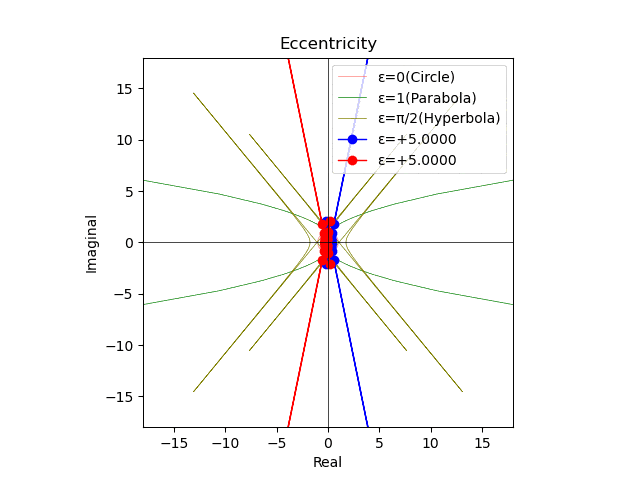
それでは実際の計算に入りましょう。
こちらも実数部平均$\bar{R}$も虚数部平均$\bar{I}$も0として、標本分散$S_R^2,S_I^2$と標本共分散$S_{RI}$は…
S_R^2=\frac{\sum_{n=1}^{2}(Ri-\bar{R})^2}{n}=\frac{(-1)^2+(+1)^2}{2}=\frac{2}{2}=1
S_I^2=\frac{\sum_{n=1}^{2}(Ii-\bar{I})^2}{n}=\frac{(+1)^2+(-1)^2}{2}=\frac{2}{2}=1
S_{RI}=\frac{\sum_{n=1}^{2}(Ii-\bar{I})(Ri-\bar{R})}{n}=\frac{(-1)(+1)+(+1)(-1)}{2}=\frac{-2}{2}=-1
不偏分散$s_R^2,s_I^2$と不偏共分散$s_{RI}$は…
s_R^2=\frac{\sum_{n=1}^{2}(Ri-\bar{R})^2}{n-1}=\frac{(-1)^2+(+1)^2}{2-1}=\frac{2}{1}=2
s_I^2=\frac{\sum_{n=1}^{2}(Ii-\bar{I})^2}{n-1}=\frac{(+1)^2+(-1)^2}{2-1}=\frac{2}{1}=2
s_{RI}=\frac{\sum_{n=1}^{2}(Ii-\bar{I})(Ri-\bar{R})}{n-1}=\frac{(-1)(+1)+(+1)(-1)}{2-1}=\frac{-2}{1}=-2
相関係数rを標本共分散で計算した場合…
r=\frac{S_{IR}}{\sqrt{S_R^2}\sqrt{S_I^2}}=\frac{1}{\sqrt{1}\sqrt{1}}=\frac{-1}{1}=-1
不偏共分散で計算した場合…
r=\frac{s_{RI}}{\sqrt{s_R^2}\sqrt{s_I^2}}=\frac{2}{\sqrt{2}\sqrt{2}}=\frac{-2}{2}=-1
線型方程式$y=a_Rx+b_R,x=a_Iy+b_I$について、切片$b_R,b_I$は共に0としてその傾き$a_R,a_I$を標本共分散で計算した場合…
a_R=\frac{S_{RI}}{S_R^2}=\frac{-1}{1}=-1
a_I=\frac{S_{RI}}{S_I^2}=\frac{-1}{1}=-1
不偏共分散で計算した場合…
a_R=\frac{s_{RI}}{s_R^2}=\frac{-2}{2}=-1
a_I=\frac{s_{RI}}{s_I^2}=\frac{-2}{2}=-1
そもそも相関係数rや線型方程式$y=a_xx+b_x,x=a_yy+b_y$の傾き$a_x,a_y$の値が負となる時には、共分散の値が負となっているのですね。
「傾き」概念の導入
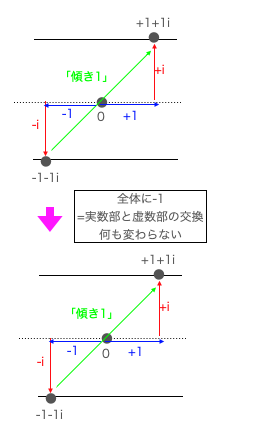
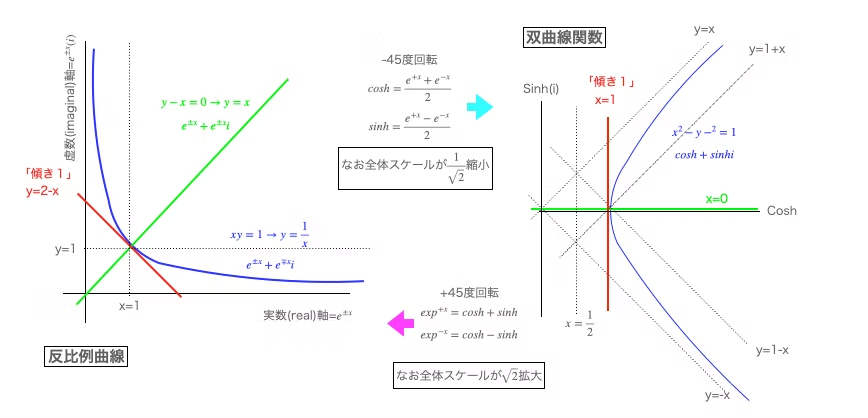
これまでのデータが-1を掛けても(xとyを入れ替えても)結果が変わらなかったのは「傾き1」だったからです(実は見た目に現れないだけで立拠する円筒座標系も直交するそれに推移)。
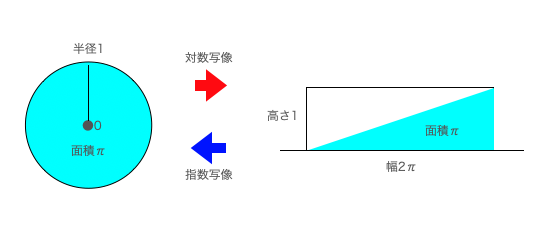
【Token】線形関数と反比例関数の連続性
この辺りの話は「底がネイピア数e(2.718282…)の指数関数は微積分しても形が変わらない」話と密接な関係があります。要するに加法群(線型方程式y=ax)における「傾き1」 に対応するのが乗法群(指数・対数関数)におけるネイピア数e(2.718282…)なのです。
【Token】ネイピア数
- 指数関数$a^x$の指数写像は、まず底の変換公式$a^x=e^{log(a)x}$を使ってlog(a)x。したがって底がネイピア数e(2.718282…)の場合の指数写像は「傾き1」となる。
- 指数関数$a^x$を微分すると$log(a)a^x$、積分すると$\frac{a^x}{log(a)}+C$.したがって底がネイピア数e(2.718282…)の場合、微分の結果も積分の結果も$e^x(+C)$となる。
こちらも実数部平均$\bar{R}$も虚数部平均$\bar{I}$も0として、標本分散$S_R^2,S_I^2$と標本共分散$S_{RI}$は…
S_R^2=\frac{\sum_{n=1}^{2}(Ri-\bar{R})^2}{n}=\frac{(-\frac{1}{2})^2+(+\frac{1}{2})^2}{2}=\frac{\frac{1}{2}}{2}=+\frac{1}{4}
S_I^2=\frac{\sum_{n=1}^{2}(Ii-\bar{I})^2}{n}=\frac{(-1)^2+(+1)^2}{2}=\frac{2}{2}=+1
S_{RI}=\frac{\sum_{n=1}^{2}(Ii-\bar{I})(Ri-\bar{R})}{n}=\frac{(-\frac{1}{2})(-1)+(+\frac{1}{2})(+1)}{2}=+\frac{1}{2}
不偏分散$s_R^2,s_I^2$と不偏共分散$s_{RI}$は…
s_R^2=\frac{\sum_{n=1}^{2}(Ri-\bar{R})^2}{n-1}=\frac{(-\frac{1}{2})^2+(+\frac{1}{2})^2}{2-1}=\frac{\frac{1}{2}}{1}=+\frac{1}{2}
s_I^2=\frac{\sum_{n=1}^{2}(Ii-\bar{I})^2}{n-1}=\frac{(+1)^2+(-1)^2}{2-1}=\frac{2}{1}=+2
s_{RI}=\frac{\sum_{n=1}^{2}(Ii-\bar{I})(Ri-\bar{R})}{n-1}=\frac{(-\frac{1}{2})(-1)+(+\frac{1}{2})(+1)}{2-1}=\frac{1}{1}=+1
相関係数rを標本共分散で計算した場合…
r=\frac{S_{IR}}{\sqrt{S_R^2}\sqrt{S_I^2}}=\frac{\frac{1}{2}}{\sqrt{1}\sqrt{\frac{1}{4}}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1
不偏共分散で計算した場合…
r=\frac{s_{RI}}{\sqrt{s_R^2}\sqrt{s_I^2}}=\frac{1}{\sqrt{2}\sqrt{\frac{1}{2}}}=\frac{1}{1}=+1
線型方程式$y=a_Rx+b_R,x=a_Ry+b_I$について、切片$b_R,b_I$は共に0としてその傾き$a_R,a_I$を標本共分散で計算した場合…
a_R=\frac{S_{RI}}{S_R^2}=\frac{\frac{1}{2}}{\frac{1}{4}}=\frac{4}{2}=+2
a_I=\frac{S_{RI}}{S_I^2}=\frac{\frac{1}{2}}{1}=+\frac{1}{2}
不偏共分散で計算した場合…
a_R=\frac{s_{RI}}{s_R^2}=\frac{1}{\frac{1}{2}}=+2
a_I=\frac{s_{RI}}{s_I^2}=\frac{1}{2}=+\frac{1}{2}
なるほど①相関係数は「水平軸の傾き成分」と「垂直軸の傾き成分(前者の逆数)」を掛け合わせて除去した残差。②逆に線型方程式y=ax+bの傾きを取り出す際には片方の成分だけ除去する、基本的にそういう考え方なのですね。
- そして円錐座標系においては一応、それなりに工夫すればここで観察した「傾き」を「頂点から底面に下された辺の回転」として規定する事が可能だったりする(まず45度回転が必要)。
【Token】二次元方眼/複素平面に埋め込まれた2^(1/2)螺旋

不偏推定量をめぐる諸問題
すると、もしかしたら標準化措置(Standardization)$\frac{x-\bar{x}}{σ}$を施すと「傾き成分」は消えてしまうのでは?
6-2. データを標準化してみよう
上掲の「傾き2」のデータで試してみましょう。まず標本分散を用いて標準化された実数部$StR$と虚数部$StI$を求め、その共分散$S_{StRStI}$を導出します。
こちらも実数部平均$\bar{R}$も虚数部平均$\bar{I}$も0として、標本分散$S_R^2,S_I^2$と標本共分散$S_{RI}$は…
StR=\frac{R-\bar{R}}{\sqrt{S_R^2}}=\frac{(-\frac{1}{2},+\frac{1}{2})}{\sqrt{\frac{1}{4}}=\frac{1}{2}}=(-1,+1)
StI=\frac{I-\bar{I}}{\sqrt{S_I^2}}=\frac{(-1,+1)}{\sqrt{1}=1}=(-1,+1)
S_{StRStI}=\frac{\sum_{n=1}^{2}StR*StI}{n}=\frac{(-1)(-1)+(+1)(+1)}{2}=\frac{2}{2}=+1
まず次いで分散を用いて標準化された実数部$stR$と虚数部$stI$を求め、その共分散$S_{stRstI}$を導出します。
stR=\frac{R-\bar{R}}{\sqrt{s_R^2}}=\frac{(-\frac{1}{2},+\frac{1}{2})}{\sqrt{\frac{1}{2}}=\frac{1}{\sqrt{2}}}=(-\sqrt{2},+\sqrt{2})
stI=\frac{I-\bar{I}}{\sqrt{s_I^2}}=\frac{(-1,+1)}{\sqrt{2}}=(-\frac{1}{\sqrt{2}},+\frac{1}{\sqrt{2}})
s_{stRstI}=\frac{\sum_{n=1}^{2}stR*stI}{n-1}=\frac{(-\sqrt{2})(-\frac{1}{\sqrt{2}})+(+\sqrt{2})(+\frac{1}{\sqrt{2}})}{1}=\frac{2}{1}=+2
相関係数rを標本共分散で計算した場合…
r=\frac{S_{StRStI}}{\sqrt{S_R^2}\sqrt{S_I^2}}=\frac{1}{\sqrt{1}\sqrt{\frac{1}{4}}}=\frac{1}{\frac{1}{2}}=+2
不偏共分散で計算した場合…
r=\frac{s_{stRstI}}{\sqrt{s_R^2}\sqrt{s_I^2}}=\frac{2}{\sqrt{\frac{1}{2}}\sqrt{2}}=\frac{2}{1}=+2
線型方程式$y=a_Rx+b_R,x=a_Ry+b_I$について、切片$b_R,b_I$は共に0としてその傾き$a_R,a_I$を標本共分散で計算した場合…
a_R=\frac{S_{StRStI}}{S_R^2}=\frac{1}{\frac{1}{4}}=\frac{4}{1}=+4
a_I=\frac{S_{StRStI}}{S_I^2}=\frac{1}{1}=+1
不偏共分散で計算した場合…
a_R=\frac{s_{stRstI}}{s_R^2}=\frac{2}{\frac{1}{2}}=+4
a_I=\frac{s_{stRstI}}{s_I^2}=\frac{2}{2}=+1
どうしてこんなにも悲惨な結末に?(涙)
- まず大前提として「標準化されたデータは傾きについての情報を失う」という考え方自体は間違っていない様である。上の計算でも標本分散を巡る途上でStR=(-1,+1),StI=(-1,+1)と変換されており、このデータから出発すると一番最初の計算の様に「標本共分散=1,相関係数1,傾き1」としかなり得ない。標準化そのものが「データセットを平均0,分散1に揃える操作」なのだからこれ自体はもう自明の場合といってよかろう。要するに上の計算はまず「以降も変換前の分散を使い続けようとした」点に問題があった訳であった。
- 「不偏標準偏差」についてはその理解からして間違っていて、それは「(単一観測データの)分散そのもの」ではなく「(複数の観測データの)分散のバラツキ具合の推定」に使うものなので、こういう「平均が確実に分かってる場合」に使冪ものではなかった様である。
標本分散と標本不偏分散,nで割るかn-1で割るか,不偏標準偏差の話題も含めて
母平均は母集団分布の位置を表す母数だが,これは,最低限として(誤差は最大になるが),測定値1個からなる標本(n=1)で足りる。ネズミとゾウの体重を比べる時,最低,ひとつの測定値があれば,非常に大雑把だが,これらの生物の体重を推測し比較できる。だから,標本平均では,分母nとして,母平均が求められる。n=0 は駄目だが,n−1 ならば,「自由に」使える,のである。それを分母で表現している。
一方,バラツキの母数である母分散は,一つの測定値では推定できない。例えば,A 組のある生徒1人の体重が 50kg,B 組のある生徒1人の体重が 60kg であったとして,どちらの組の生徒の体重がバラツキが大きいか,と問われても,さっぱりわからない。この場合,体重のバラツキを推定しようとしたら,最低限もうひとつ,つまり各組2人ずつの測定値が必要だと分かる。これが母分散を求めるときの自由度n−1 につながる。n=1では不可(分母が0になる),n≥2ならば自由に使える,ということを分母で示している。
計算的には標準誤差(Standard Error)、より厳密には平均の標準誤差(Standard Error of the Mean, SEM)の概念から出発する様です。nを標本サイズ(観測回数)として…
SE=\sqrt{\frac{σ^2}{n}}=\frac{σ}{\sqrt{n}}
この分布は、標本サイズが大きくなるほど中心極限定理によって,次第に正規分布に近づき、その様子は以下の式で表されます。母分散$σ^2$について、標本分散$s^2$の平均$\bar{S^2}$と標本平均の分散$\frac{σ^2}{n}$を用いて説明を試みるなら…
\lim_{n→∞}\bar{S^2}+\frac{σ^2}{n}=σ^2
この式を変形すると「n-1」が現れます。
\bar{S^2}=(1-\frac{1}{n})σ^2=\frac{n-1}{n}σ^2
両辺に$\frac{n-1}{n}$を乗ずると…
\frac{n-1}{n}\bar{S^2}=σ^2
ところで標本分散の計算式は以下なので…
S^2=\sum_{i=1}^n\frac{(X-\bar{X})^2}{n}
これに$\frac{n-1}{n}$を乗ずると、やっと見慣れた式形に到達する訳です。
s^2=\frac{n-1}{n}S^2=\sum_{i=1}^n\frac{(X-\bar{X})^2}{n-1}
ところで、これまで行ってきた計算は「(複数の観測データの)分散のバラツキ具合の推定」を想定しておらず、暗黙理にそこは「1」として計算してきました。だから標本分散を使った計算の方が通ったという次第…
こうしてなんとか以下の線型結合式が見えてきました。
観測データ=(…,勾配*標準化されたデータ間の相関係数,…)
それにつけても何故2乗? 偏差がそのまま合計すると±0になってしまう問題なら、絶対値を取ってもいい筈で、実際そういう研究もあったりします。
平均(Mean)と標準偏差、中央値と平均偏差
この話、最小二乗法のの発案者候補者にして尤度(likelihood)概念の発案者でもある数聖ガウス(Carolus Fridericus Gauss、1777年~1855年)が誤差関数発明に際して…
- 小さな誤差ほど比較的観測され易い。
- 大きな誤差ほど比較的観測され難い。
- 従って、一定以上の誤差を切り捨てる事によって観測精度(Observation Accuracy)を確定する事が出来る筈である。
なるアイディアを式形$\frac{1}{\sqrt{π}}\int_{n=-∞}^{+∞}e^{-x^2}$と表現した時点にまで遡る訳ですが…
誤差関数と相補誤差関数
数聖ガウスが同時に複素平面概念の発案者候補者にも名前を連ねており、複素平面上でなら誰でも容易に$1=-i^2$なる変換を誰にでも思いつける辺りから話がややこしくなってきます。
まぁこの式を思いついただけではどうしようもなく、その面積を求め、それで割る事によって「面積1の確率空間」を現出させた事にこそ、彼の天才性があった訳ですが。
ガウス積分の公式の2通りの証明
もちろん中心極限定理の概念自体はそれ以前まで遡り、ガウスがこの式形を与え「ガウス分布」なる呼称が定まる以前も以降もそれは自然観察のあらゆる場面に現れる事実は揺らぎません。この時彼が発表した仮説の本質はあくまで「誤差もガウス分布する」という内容で、しかもその正さはたちまち膨大な実証データによって裏付けられる結果となったのです。
17-3. 中心極限定理1
複素数空間にようこそ?
今から思えば私が「正比例関数と反比例関数の連続性」の件や…
【Token】反比例関数と指数対数関数の回転

「反比例関数と双曲線関数の連続性」の件や…
【Token】二次元方眼/複素平面に埋め込まれた2^(1/2)螺旋
「相関係数の図示化」の件に取り組んできたのは…

みんなそれを連続演算で結ばれた一つの多様体として表現したいという最終意図実現の為でした。
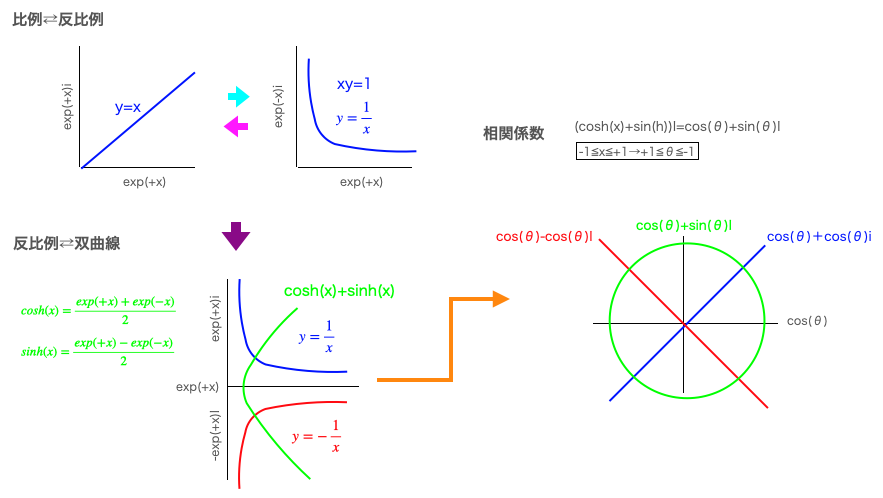
その鍵を握るのが円錐曲線である事も浮かび上がってきました。
【Token】円錐座標系

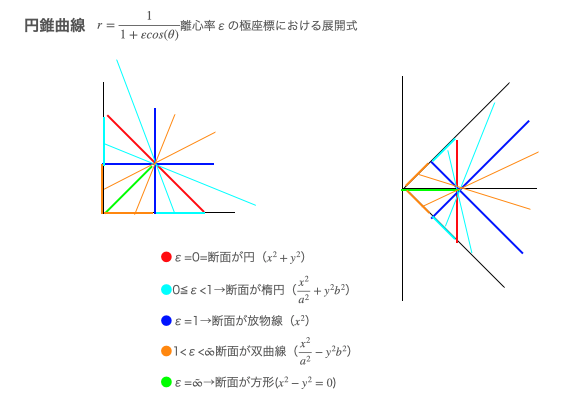
ここで興味深いのが「傾き1」の座標上での表し方には「x=9とy=0の対」と「y=xとy=-xの対」の蓋通りあり、円錐曲線においてはその組み合わせによって断面が「円」とも「放物線」ともなり得る辺り。
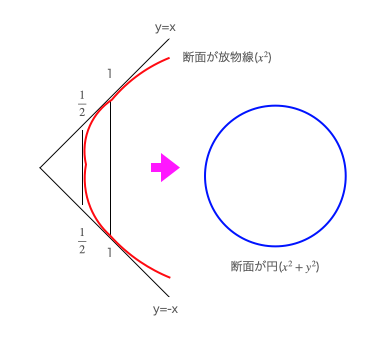
なんとかそこまで辿り着いた時点で以下続報…
【追記1】「欲しかった答え」への「欲しかった形」での到達
「叩けよ、さらば開かん」といいますが、ここまで問題意識を煮詰めてやっと次の段階に進む事が出来ました。鍵は「統計計算から行列計算に」「数学問題から物理問題へ」頭を切り替える事だったのです。
- 一般に行列演算を使って連立方程式を解く場合には係数行列の逆行列を求めるが、この方法が完全な形で通用するのは、その係数行列が正方行列(行と列の数が等しい行列)の場合に限られる(初学者問題)。
うさぎでもわかる線形代数 第03話 逆行列を使って連立方程式を解く - ただし擬似逆行列を使えば近似的に解けないでもない(これもまた比較的初学者問題)。
うさぎでもわかる線形代数 応用編第8羽 擬似逆行列 (一般化逆行列) - 実はこの「近似的に解けないでもない」方法こそが最小二乗法への入り口。
うさぎでもわかる線形代数 応用編第9羽 行列を使って最小2乗法を解いてみよう!
なんと、私が突き当たっていたのは「受験問題には解けない問題があってはならない受験数学の壁」だったのです。まさにこの話題こそが機械学習理論への入り口だというのに!!
マンガ 線形代数入門

そしてここでも「結果が線形方程式となる事が観測的に確かめられる抵抗値の性質」が重要な理解の助けに。とどのつまり現実世界にはかくも容易く「代数的に解くには式が多過ぎる(線形代数を駆使してても近似しか出来ない)連立方程式」が顕現し、それを解く為に開発された様々な技法が最終的に機械学習論に集約されてきた訳です。何たる学習モチベーションの源泉‼︎ 日本の未来の為にも、この考え方に是非広まって頂きたい…
大学物理のフットノート オームの法則
そういえば人類が最小二乗法の概念に到達したのも地球の大きさを測ろうとしたのが契機でした。
地球の大きさと最小2乗法
しかも歴史のその時点ではルシャンドルやガウスの様な数学的天才だけに到達を許された領域を(しかも、かの「数聖」ガウスでさえ最初は後出しジャンケンっぽい関わり方しか出来なかった感がある)、誰もが気軽に追試可能な形に整備したのが(分散概念に立脚する)統計学や(数字の対角配置を重視する)行列演算の発明だったという事は「数学の枠組みだけで考えていては、数学の全体像は分からない」という困った話に。
【追記2】とりあえず全体像のまとめなおし。
こうして全体像を俯瞰してみると、相関係数の正体はどうやら、以下の複素円錐座標系の「実数部のみの流用」という辺りに話が落ち着きそうですね。
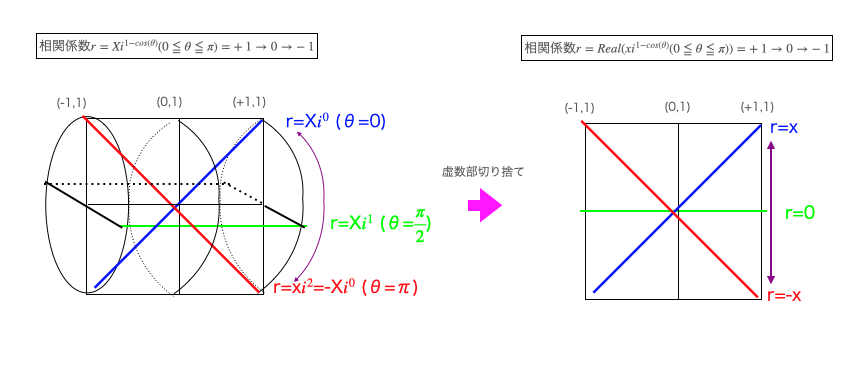
電気工学分野での虚数の利用法と似ています。要するに「高次元概念を導入したいが、わざわざ次元拡張するまでもない(迂闊に次元拡張すると問題解決が変な方向に複雑化する)」ケースで有効なアプローチという次第。
電気の交流では何故虚数が必要なのですか - OKWave
X軸でなくY軸を実数部に射影しても結果は変わりません。というより、自然に考えると…
- 傾きが1以下の場合は(x軸に沿った)横回転の円錐座標系が選ばれる。
- 傾きが1以上の場合は(y軸に沿った)縦回転の円錐座標系が選ばれる。
そういう振り分けになる感じ?
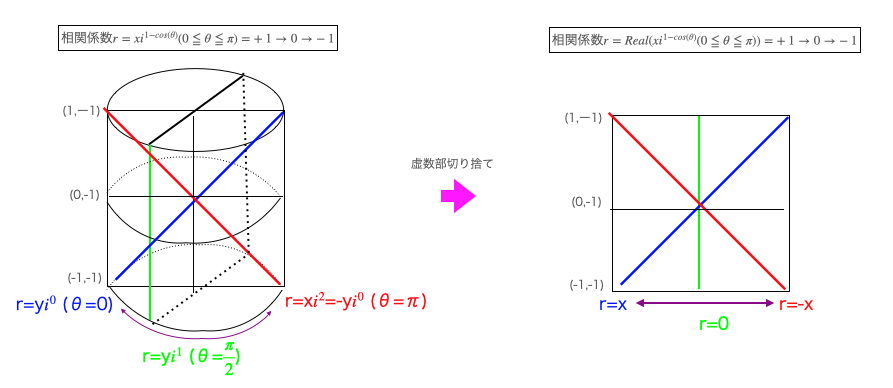
X座標軸とY座標軸の交換は複素座標系における実数部と虚数部の交換に該当します。つまりこの方法もまた「(3次元空間に3対セットで配置される)円錐座標系を乗り換え」に対応する訳です。

平面で考える限り、こうした次元操作の違いは表面化してきませんが(xy=yx、いわゆる「可換性」の正体)、三次元で考えた場合「(3次元空間に3対セットで配置される円錐座標系の)3番目の円錐座標系」との符号関係の逆転が生じます。ここでi軸、j軸、k軸を中心とするとする3対の複素円筒/円錐座標系の関係に目を向けると…
ij=k,ji=-k,jk=i,kj=-i,ki=j,jk=-j
まさしく「ハミルトンの四元数(Hamilton's quaternion)」そのものの振る舞い。
【Token】「ハミルトンの四元数」
【Token】屋根掛け法
突然話がややこしくなってきますが、「実数部しか使わない」事によって、こうした「操作上の煩雑さの発生」に対して隔壁を落とす訳です。その一方で相関係数を「そういうもの」と定義してしまうと、残りの部分は吃驚するほど単純化されるのです。まずは上掲の相関係数計算過程…
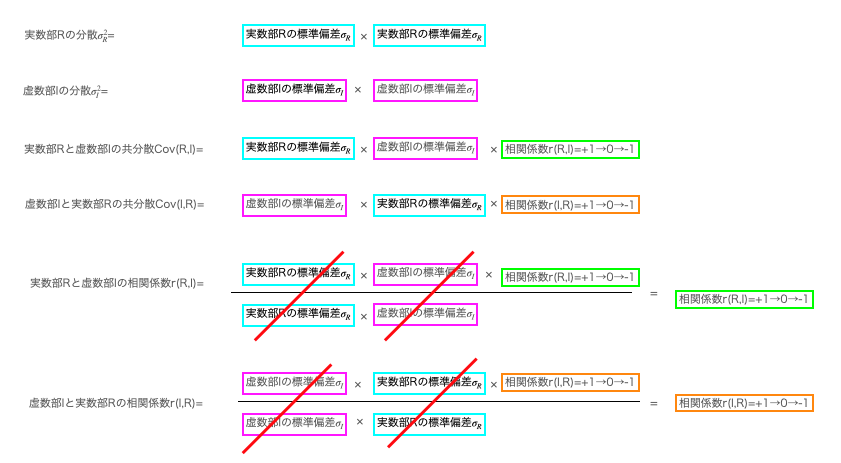
次いで最小二乗法による傾きの取得過程。2データの標準偏差比は、両データの相関係数が±1の時に傾きそのものですが、相関係数の絶対値が下がる都度目減りして、相関係数0の時は傾きも必ず0になってしまいます。
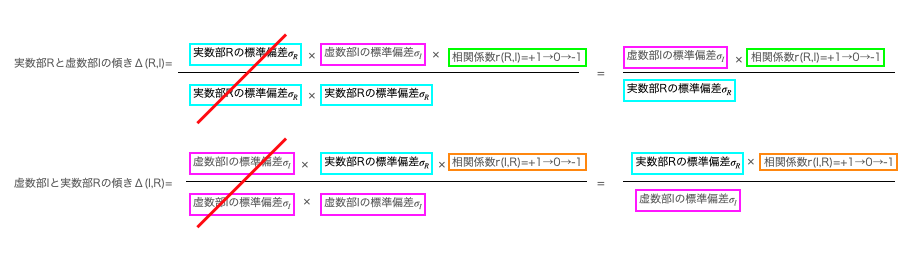
そしてデータ標準化の影響。傾き情報を放棄した結果、共分散がそのまま相関係数に。

とどのつまり…
- 2データの標準偏差比は、両データの相関係数が±1の時に傾きそのものとなる(相関係数の絶対値が下がる都度目減りして、相関係数0の時は傾きも必ず0になってしまう)→「先に相関係数が十分大きい事を確認してからでないと、最小二乗法で傾きや切片を求める意味はない」経験則の数式表現。
最小二乗法①数学的性質
* この範囲の計算自体は(推測統計概念を特徴づける)正規分布概念などに全く依存しない。すなわち完全に記述統計概念の中で完結している→最小二乗法は外れ値に極めて弱く、これを除去する為に誤差関数概念を導入して以降が推測統計概念の世界となる。
【Token】「何も起こってない」ディフォルト状態としての正規分布
* 逆をいえば、この範囲の計算内には「偏差を単純合計しただけでは総和が0になってしまう」問題を解決するのに、どうして(絶対値などではなく)二乗するのか? という質問への答えもまた含まれていないという事になる。
【初心者向け】平均と標準偏差、中央値と平均偏差
いっちゃなんですが、全ての混乱の大元は「ガウスが誤差関数概念を発見した時点では、ハミルトンの四元数概念も分散概念も未発見だった」事にあるのではないでしょうか。当時の行列演算概念はまだまだ発展途上だったので、単位元概念の自然な拡張として以下の様な簡潔かく的確なイメージを思い浮かべる事が出来なかったのです。
相関行列の定義と分散共分散行列との関係
アフィン変換(平行移動、拡大縮小、回転、スキュー行列)
単位元\begin{pmatrix}
1 & 0 \\
0 & 1 \\
\end{pmatrix}→
相関行列\begin{pmatrix}
1 & r(R,I) \\
r(R,I) & 1 \\
\end{pmatrix}
「傾き」概念の同時座標系表現\begin{pmatrix}
Δx & 0 & 0\\
0 & Δy & 0\\
0 & 0 & 1\\
\end{pmatrix}
相関行列と分散共分散行列の関係\begin{pmatrix}
1 & r(R,I) \\
r(R,I) & 1 \\
\end{pmatrix}
=\begin{pmatrix}
\frac{1}{σ_R} & 0 \\
0 & \frac{1}{σ_I} \\
\end{pmatrix}
\begin{pmatrix}
σ_R^2 & Cov(R,I) \\
Cov(R,I) & σ_I^2 \\
\end{pmatrix}
\begin{pmatrix}
\frac{1}{σ_R} & 0 \\
0 & \frac{1}{σ_I} \\
\end{pmatrix}