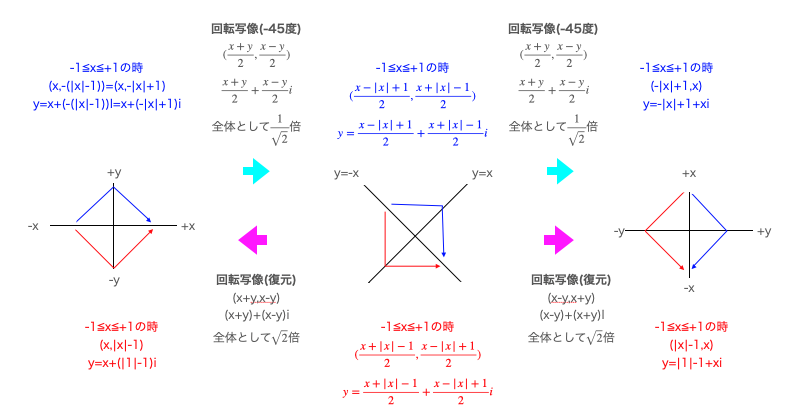
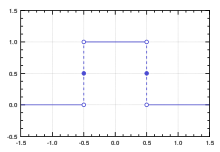
複素平面a+biと異なり、二次元方眼(x,y)には$2^{\frac{1}{2}}$螺旋が埋め込まれています。
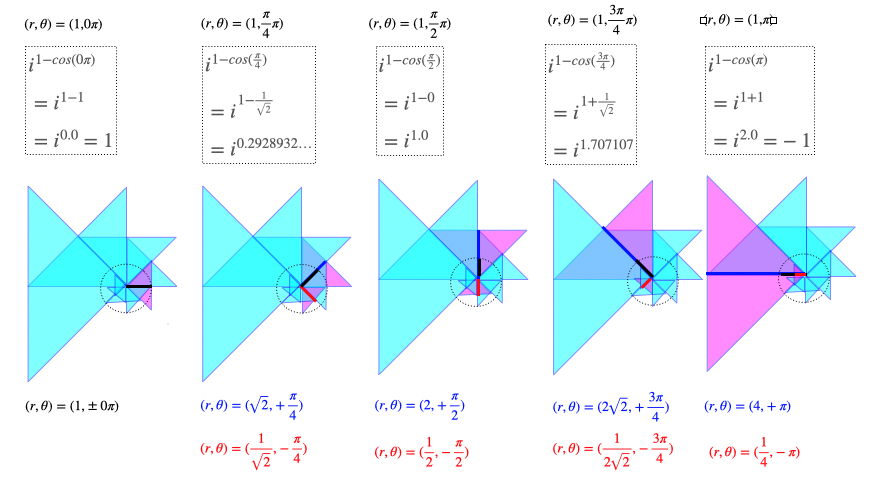
- 虚数(Imagical)の定義$i^2=1$を変換すると$a^{2\log_a(i)}$となり、これが円を描くのはaがネイピア数e(2.718282…)の場合のみ。
【Token】ネイピア数

- この時、式は$e^{2log(i)}=e^{2\frac{π}{2}i}=e^{πi}$と変形され、オイラーの等式$e^{πi}=-1$に一致する。
Wikipedia「オイラーの等式」 - 数学史を辿ってみると、この様に二次元方眼上での円回転をイメージ可能となったのは19世紀前半にガウスらが複素平原の概念を導入して以降だし、さらにいわゆる「矢印ベクトル」概念が導入されたのは1843年に導入された「ハミルトンの四元数」概念があまりに難解なので、その簡略版として「矢印ベクトル」概念が普及した19世紀後半から20世紀初頭にかけてとなる。
【Token】「ハミルトンの四元数」

- こう考え合わせていくと、現代の我々が見知ってる二次元方眼概念そのものが(特に近代以降急激に次元概念拡張を重ねてきた)多様体(Manifold)概念の代表例ということになる。
コトバンク「多様体」
方形関数(Rectangular Function)の勘所
絶対値関数の扱いで面倒臭いのは、その演算上の特徴故に、必ず「下が凸となる形が正方向になる」事。
y=x→y=|x|
y=-x→y=|-x|=|x|
従って方形関数の形も以下となるのです。
y=±(|x|-1)
45度回してみましょう。
(x(-1≦x≦+1),|x|-1)→(\frac{x+|x|-1}{2},\frac{x-|x|+1}{2})
(x(-1≦x≦+1),-|x|+1)→(\frac{x-|x|+1}{2},\frac{x+|x|-1}{2})
xに三角関数を代入すると回せます。
Cos01<-function(Radian){
c0<-seq(0,pi*2,length=61)
cx<-cos(c0)
cy=c((1-abs(cos(c0[1:30]))),-(1-abs(cos(c0[31:61]))))
plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Cos(θ)±(1-abs(Cos(θ)))i",xlab="x=Cos(θ)",ylab="y=±(1-abs(±Cos(θ)))i")
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
# θ位置を書き添える 。
text(cx[Radian],cy[Radian],"θ",col=rgb(0,1,0))
segments(0,0,cx[Radian],cy[Radian],col=rgb(0,1,0))
# 凡例を書き添える 。
legend("topright", legend=c("y=Cos(θ)±(1-abs(Cos(θ)))i","x=y=0","x=Cos(θ)"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,1,0)))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Cos01(i)
}
}, interval = 0.1, movie.name = "Cos09.gif")
Sin00<-function(Radian){
c0<-seq(0,pi*2,length=61)
cx<-sin(c0)
cy=c(1-sin(c0[1:15]),-(1-sin(c0[16:30])),-(1+sin(c0[31:45])),1+sin(c0[46:61]))
plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Sin(θ)±(1±sin(θ))i",xlab="x=Sin(θ)",ylab="y=±(1±sin(θ))i")
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
# θ位置を書き添える 。
text(cx[Radian],cy[Radian],"θ",col=rgb(0,1,0))
segments(0,0,cx[Radian],cy[Radian],col=rgb(0,1,0))
# 凡例を書き添える 。
legend("topright", legend=c("y=Sin(θ)±(1±sin(θ))i","x=y=0","x=Sin(θ)"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,1,0)))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Sin00(i)
}
}, interval = 0.1, movie.name = "Sin12.gif")
また、矩形関数にはこちらの考え方もあります。
Wikipedia「矩形関数」
rect(t)=\left\{
\begin{array}{ll}
0 & (|t|>\frac{1}{2}) \\
\frac{1}{2} & (|t|=\frac{1}{2}) \\
1 & (|t|<\frac{1}{2})
\end{array}
\right.
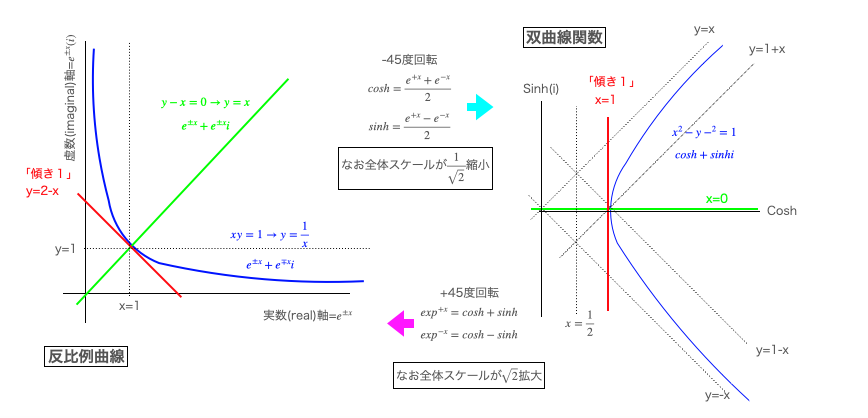
反比例関数(Inverse Proportional Function)/双曲線関数(Hyperbolic Function)の場合
反比例関数(Inverse Proportional Function)は45度回転させると双曲線関数(Hyperbolic Function)と重なります。
そんな感じで以下続報…