一般に「統計的尺度水準」といった場合、以下を指します。
Wikipedia「尺度水準(Level of measurement)」
調査対象に割り振った変数、その測定、あるいはそれにより得られたデータを、それらが表現する情報の性質に基づき数学・統計学的に分類する基準である。スタンレー・スティーヴンズ(Stanley Smith Stevens)が1946年に論文「測定尺度の理論について」"On the Theory of Scales of Measurement"で提案した分類がよく用いられる。
変数に対して可能な数学的操作は、変数を測定する尺度水準に依存し、その結果特に統計学で用いるべき要約統計量および検定法も変数の尺度水準に依存する。また、扱っている数の範囲が実数全体なのか正の実数全体なのかを区別することも重要である。
スティーヴンズは低い方から順に以下の4つの尺度水準を提案しており、高い水準はより低い水準の性質を含む形になっている。また高い水準でのデータを低い水準に変換して扱うことができる。
スティーヴンズの尺度水準
- 名義尺度(Nominal Scale)
- 順序尺度(Ordinal Scale)
- 間隔尺度(Interval Scale)
- 比例尺度(Proportional Scale)
いかんせん「制定1946年」。統計学なる分野が順調に進化を遂げてきた結果、色々綻びが見えてきた様に思えるのです。どのあたりがそうなのかについて調べてみる必要がありそうです。
名義尺度(Nominal Scale)
まずはWikipediaの記述から。
類別尺度ともいう(石井 1975)。この水準では数字を単なる名前として対象に割り振る。2つの対象に同じ数字がついていればそれらは同じカテゴリに属する。変数値間の比較は等しいか異なるかでしか行えない。順序もないし加減などの演算もできない。例えばISO5218は、ヒトの性別に数値を割り当てているが、「女性は男性の2倍である」「法人は女性の4.5倍である」という意味にならない。
例としては電話番号、背番号、バスの系統番号など。代表値の指標として使えるのは最頻値のみである。統計的バラツキは変動比や情報エントロピーで評価できるが、標準偏差などの概念はありえない。名義尺度でのみ測定されるデータはカテゴリデータとも呼ばれる。
なおカテゴリデータを、ある性質が「あるかないか」という表現に直し、さらにこれを「1か0か」で表現したものをダミー変数という。ダミー変数またはそれから算出されるスコア(点数)を、順序尺度以上の水準に準じて扱う方法もよく用いられる。
私はこれを「単極球状体(Monopolar Sphere)表面上の任意の点の間の関係」に見立てました。「傾き1」の数式表現は以下の様に(-1-1i,+1+1i)となる訳ですが…
【Token】相関係数と線形回帰
我々人類は概ねこの考え方を「二次元空間に敷き詰められた平方眼(正方形=デカルト座標系の世界)」とか「三次元空間に敷き詰められた立方眼(立方体=「ハミルトンの四元数」の世界)」くらいにしか拡充出来ず、その次にいきなり現れるのがこの「N次元対角線の集合体」としての単極球状体という次第。
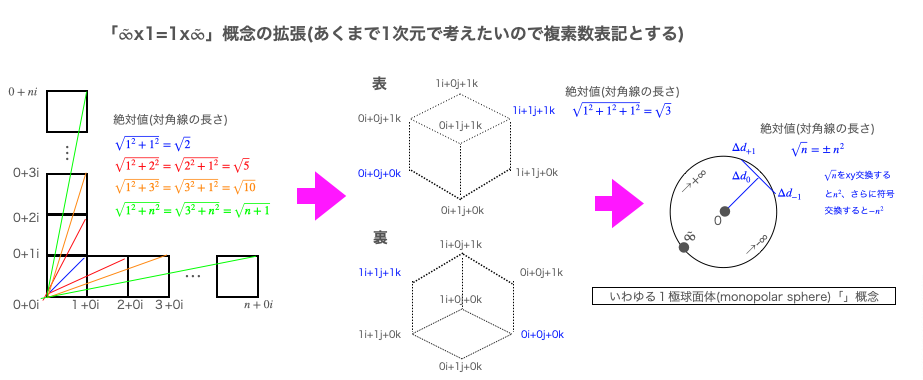
- ここでいう0はN次元座標の中心=「0がn個続く座標」に該当
- 中心から下された垂線は円弧/球面上の任意の微小辺$Δd(Δd_{-1},Δd_{0},Δd_{+1}$の3点を結ぶ直線)と直交する。
- その一方でn次元対角線の性質上、角$Δd_{-1}Δd_{0}Δd_{+1}$は直角を為す筈である。
- この矛盾から実測される1極球面体上の任意の点は原則として名義尺度 (Nominal Scale)のみを構成する。
- またこの1極球面体に直径の概念はない。
その上この単極球面体、いわゆる指数写像(Exponential Map)や対数写像(Logarithmic mapping)が実施される作業空間を準備する「ネイピア数e(2.718282…)を底とする連続テトレーション演算」の極限(曲率±∞)でもありまして「距離が計測不能」なる特徴を有していたりします。
【Token】物理学と数学の接点について。
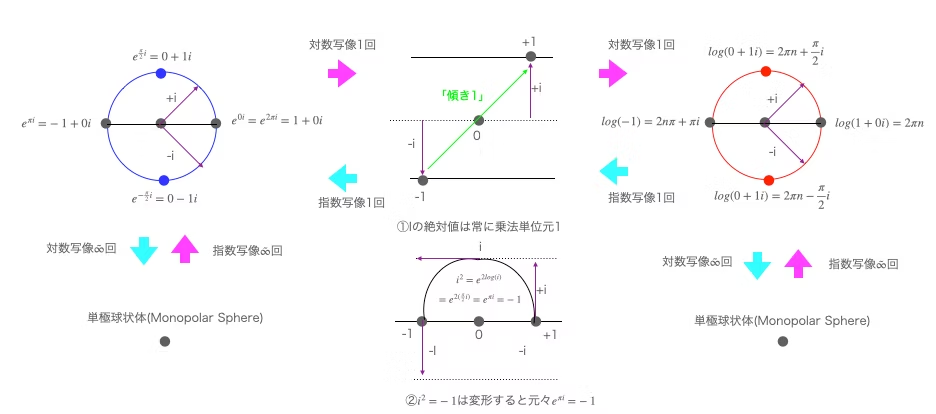
「距離が計測不能」という事は。以下のイメージのどれが正しく、どれが間違っているかすらいえない状況。
- 点(球表面上の任意の点の半径全てが0)
- 無限大球面(球表面上の任意の点の半径全てが$\tilde{∞}$)
- 単位球面(球表面上の任意の点の半径全てが1。無限大球面の逆元)
- 「尿道結石」状態(球表面上の任意の点の半径がそれぞれ0から$\tilde{∞}$の間)
最後の「尿道結石」状態のイメージの源泉は、まさしく「八重洲ミッドタウン前に建っているあの彫刻」だったりします。

なんだか突拍子もない際物としか思えませんが、しばしば「大航海時代の地図作成過程」に自らを擬える「部分的にしか(設定に成功した範囲でしか)ユークリッド距離空間が現れない」多様体(Manifold)概念における「観測の旅に出発する以前の地図作成者のタブララサ状態な脳内」と考えれば「世界の果ての滝で待ち構えてる海龍」なんぞを含まないだけ、よっぽど科学実証主義的といえましょう。
多様体の基礎のキソ
コトバンク「タブララサ(tabula rāsa)」
分類尺度(Classification Scale)
今では機械学習分野などで欠かせなくなった尺度です。当時はこれに注目する分野自体がまだ存在していませんでした。
【3分で分かる】回帰問題と分類問題の違い
「教師あり学習」仲間という事で一緒くたに語られがちな回帰分析ですが、例えばしばらく前の初学者向けの統計教科書などには、以下の様な手順指導が掲載されてました。
【Token】相関係数と線形回帰
- まずグラフ化し。肉眼にて相関可能性を探る。
- 相関係数を計算して直感が正しかったか確かめる。
- それなりの相関係数を得たら(例えば一次関数ax+bにおける傾きaと切片bを求める)回帰分析に進む。
ただし回帰分析はあくまで比例尺度や間隔尺度が成立してる前提で実施するもので、この段落で触れたい内容ではありません。ならば「分類(特に機械学習のそれ)」は、どういう手順を踏むものなのでしょうか?
- 研究対象に選ばれるのは「犬」「猫」といった「多くの人間において自明の場合となる判断」が多い。
- その一方で判断基準の方は概ね明らかになっておらず、それを仮設定して人間の判断率に近づける事自体を研究目的とする。
とりあえずこの「判断基準については明らかになってない(確率の合算結果などで単一評価軸ですらない可能性も含む)」というあたりを水準定義に採択しましょう。従ってまだ多様体定義の肝である「ユークリッド距離に基づく座標軸」は設定出来ません。
ノーバート・ウィーナー「サイバネティクス(1948年初版)」の時代まで遡ると、この辺りの研究は「ロックの観念連合説を神経系の機構によって説明しようとした」ゲシュタルト心理学の分野が担っていた様です。第6章「ゲシュタルトと普遍的概念」より。
ロックによれば、連想は隣接性、類似性、および因果の三原則に従って起こるのである。これらのうち第三の因果の原理を、ロック、さらに確定的にヒュームは、常に相伴って起きる事に過ぎないとして、第一の隣接性の定義に包含させてしまった。第二の類似性の定理については、もう少し詳細に論じる必要がある。
ある人が横から見ても斜めから見ても正面から見ても、その容貌が同一である事を見分けられるのはどうしてであろうか? 円が、大きくても小さくても、遠くにあっても近くにあっても、さらに目と円の中心を結ぶ線が面に垂直であって実際に円に見えるときも、そうでなく楕円に見えるときも、それが一つの円であると認識されるのはどうしてであろうか? どうしてわれわれは雲や、ロールシャッハ検査のインクの汚点を、顔や動物や地図と見立てるのであろうか? これらすべての例は、目に関するものであるが、他の感覚についても同様の問題が存在し、そのうちあるものは諸感覚間の関係にも関連している。われわれは鳥のさえずりや虫の鳴き声をどのようにして言葉に表現するのであろうか? 硬貨の丸みを手で触ってどうやって見分けるのであろうか?
この後「サイバネティクス」自体の記述は感覚器官と神経の通信の様な生理学的話題に推移してしまうのですが、マルチモーダルな観点に立脚するゲシュタルト心理学が「プレグナンツ(Pragmanz=簡潔さ)の法則」と名付けた「近接」「類同」「閉合」などの記憶統合概念自体は、巡り巡って機械学習時代の分布意味論にまでそれなりの形で継承される展開を迎えるのです。
名義尺度と分類尺度の峻別
ここで頭を切り替え、他にこの尺度に加えられる分類がないか物色してみましょう。例えばランチ予算が1000円未満のサラリーマンの普段の昼食のローテーションが「デパート食堂のサービスランチABC」および「近場の定食屋の日替わり定食」および「近場の中華料理屋の中華セットABC」だったとします。ミクロ経済学でいう完全代替財の集合。「店舗集合」と「メニュー集合」が二重に存在する辺りもこの尺度の特徴と言えそうです(例えば「デパート食堂のサービスランチC」は「近場の中華料理屋の中華セットA」と献立的には同じ中華定食かも知れず、そういう重複も想定される)。
しかし3月には、かつて大人気を誇った「シュクメクリ鍋定食」の限定復刻があり、そればかり毎日食べに行ったとします。もちろんこの選択肢は二月にも四月にもありません。では、それは何処から来て何処に消えたと考えるべきなのでしょうか?
ここでこの集合には「常に集合内に存在しながらカウントされない」不可視の名義尺度(単極球状体)も加わっていて、全ての選択肢はそれから分かれ、そこに再吸収されていくものと考えてみましょう。
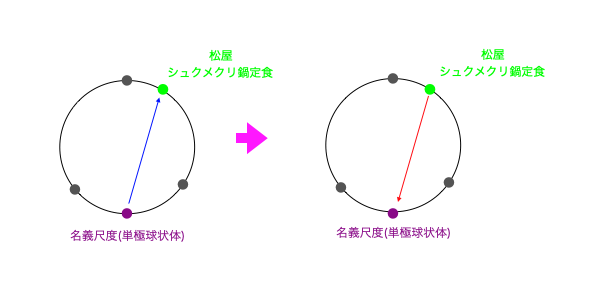
- 集合論においては「(必ずどの元もいずれかの分類に含まれるとする)閉世界仮説」を成立させるには、一番外縁の補集合(どの分類にも含まれない何かの集合)を空集合にしなければならないとされている。
この空集合を(上掲の単極球状体の性質を備えた)名義尺度元の集合と考える訳である。
ベン図と組み合わせ計算と確率演算
同様の状況を、統計学的研究でしばしば見受けられる「正規分布を帰無仮説とする棄却検定」で捉える事も出来ます。有意元集合は状況に応じて増減しますが、それは「空集合として扱われる/空集合でなければならない」名義尺度元の無意味元集合から追加され、かつ有意味性を失えばそこへと再吸収されていくのです。
- 正規分布とは要するに「何も起こってない時のデフォルトの分布」なので、それと比較して充分な相違が認められたら「有意味な何かが起こっていると証明された」と考える訳である。
帰無仮説とは?対立仮説との違いを例題でわかりやすく。検定で棄却できないときの結論は?
「元が現れたり消えたりする」イメージといえば、砂糖や絹の様ないわゆる「世界商品」のライフサイクルを連想するのも方法の一つかもしれません。それは概ね異文明などから突然もたらされ、当初は王侯貴族が贅沢を誇示する威信財として機能するも、国産化が進んだりして希少価値を失うと他の日常品の波に飲まれる形でその役割を終えるのです。
「限界効用逓減の法則を巡る数理」あるいは「愛(i)に出来る事はまだあるかい」?
なんの事はない、全てN進数における「切り捨てられる桁」概念の抽象化とでも考えればよいのです。
N進数から複素螺旋座標系へ
とにかく「名義尺度と分類尺度の峻別基準」をこの様に定めておく事にします。
順序尺度(Ordinal Scale)
まずはWikipediaの記述から。
この水準では対象に割り振られた数字は測定する性質の順序を表す。数字は等しいかどうかに加え、順序(大きいか小さいか)による比較ができる。しかし加減などの演算には意味がない。
例えば、国際原子力事象評価尺度がこれにあたる。チェルノブイリ原子力発電所事故はレベル7に評価されているが、これは「レベル6よりも上である」という意味ではあるが「レベル4の2倍に及ばない」という意味にはならない。
その他にも物理学的な例としてモース硬度がある。その他の例にはレースの着順などがあるが、これでは到着時間の差は記録できない。
心理学や社会科学の測定のほとんどは順序尺度で行われる。例えば社会的態度(保守的か進歩的かなど)や階級は順序水準で測定されるものである。また客の嗜好(アイスクリームのバニラ味とチョコレート味とどちらが好きか)のデータもこれで表現できる。順序尺度の代表値は最頻値や中央値で表されるが、中央値の方が多くの情報を与える。順序尺度で測定されるデータは順序(または順位)データと呼ぶ。
順序尺度を統計で用いる場合に、順序尺度を数値に置き換えて計算することがある。ただし、計算結果が元の順序尺度を保存していることが条件となる。
各カテゴリに属す対象の個数という形のデータにまとめると数量データと呼ばれ、これは分割表で表示できる。これらに対して用いられる統計検定法はノンパラメトリックなものに限る。
分類尺度同様、「判断基準については明らかになってない(確率の合算結果などで単一評価軸ですらない可能性も含む)」なる定義を継承します。従ってまだ多様体定義の肝である「ユークリッド距離に基づく座標軸」は設定出来ません。
また、上掲のWikipedia「尺度水準」によれば、以下のような議論もあるそうです。
行動科学で順序尺度の平均値に意味があるかどうかといった議論がなされている。数学的には意味がないが、一部の行動科学者は実際に使っている。行動科学における順序尺度は実際には順序尺度と間隔尺度の中間にある(2つのランクの差は一定ではないが、ほぼ同程度である)というのがその理由である。
順位尺度と間隔尺度の峻別
上掲の記述でミクロ経済の完全代替財について触れました。一般に直行座標系の第一象眼(座標軸がどちらもプラスのみ)を考えるミクロ経済学では、価格のみを評価軸の単位とする効用モデルについて以下の様に動くと考えます。
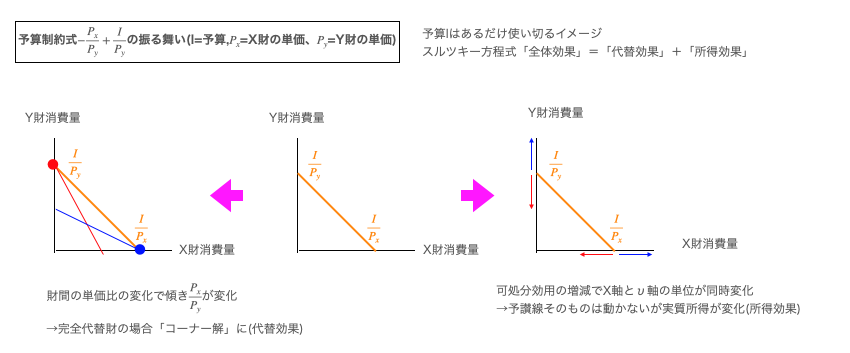
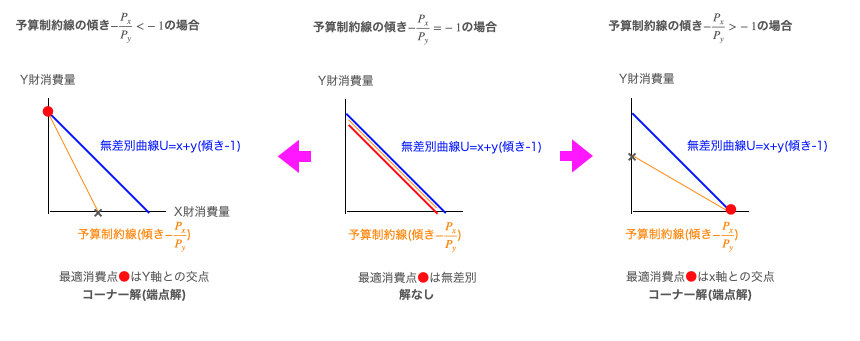
円錐座標系で全体像を捉え直すと対象が2財間の二次元関係から財集の分類問題に拡張され、また別の情景が浮かび上がってきます。例えば以下は「価格競争について来れなかった財の脱落」…
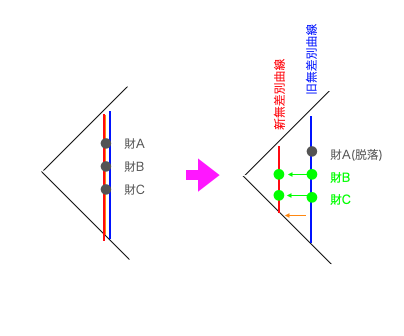
以下は「(競合相手が存在しなくなった)独立財の誕生過程」。
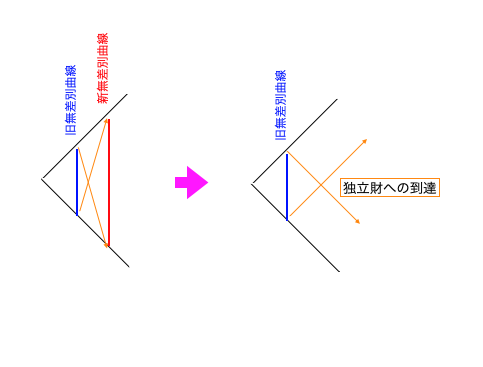
価格変化のみを扱うミクロ経済学はこうした(価格以外の効用変化も視野に置いた)過程は扱いません。「評価を特定の単軸(あるいは特定の複数の評価軸の組み合わせ)」に絞る際には、必ずこうした「評価基準の切り捨て」が発生するものです。例えばとあるマラソンのTV実況について考えてみましょう。
- スタート時点においては「参加する事に意義がある(完走のみが目標)」「コスプレを見せつけたい」など多種多様な動機を抱える参加動機も一塊で走り始める。
- しかしマラソン自体はあくまでタイムを一次元的に競う競技であり(芸術展の追加などはない)、それに従って次第にグループ分けされ、実況カメラはその先頭集団ばかり写す様になる(時々、箸休め的に「コスプレを見せつけたい」派にカメラが向けられ、お茶の間やネットを賑わせるかも知れないが、そういう要素は全て切り捨てて考えるものとする)。
- 有名選手でも体に故障を感じて先頭集団から脱落するかも知れないし、また無名のアマチュアが番狂わせで先頭集団に加わってくるかもしれない。
こうして全体像を俯瞰してみると(実況カメラが捉えている)先頭集団においては実質上「単一評価軸に従っての順序尺度(実質上の間隔尺度)」が成立する一方、そういう状況を成立させる為に残りのランナーは「実質上空集合として扱われる」名義尺度元集合として「切り捨てられた」とも考えられる訳です。
円錐曲線ではこの時断面が楕円から放物線に推移しますが(奇しくも放物線は物理学における周回運動からの脱出軌道)、ミクロ経済学はこの過程を扱いません。何故なら価格のみに注目するとこの展開では「(予算制約線に合わせた)消費量の減衰」といったまた別の展開が観測されるからです。「とあるサラリーマンのランチローテーション」の様な消費行動は、他にも沢山の判断基準を含みますが、あえてそこだけに関心を絞る事で見えてくる事もあり、その様な評価軸単一化に有意味かどうかがまさに尺度決定上、大きな意味を持つわけです。これは他に「3月限定のシュクメクリ鍋の希少価値」といった評価尺度をも出してその組み合わせで考える場合も同じで、その場合単項式が多項式に拡張されるだけなのです。
とりあえず「ただの順序尺度」と「(実質上間隔尺度として扱い得る)単一評価軸上における順位」この様に定めておく事にします。
間隔尺度(Interval Scale)と比例尺度(Proportional Scale)
間隔尺度や比例尺度の世界には、これまで見てきた様な「実質空集合として扱われる(空集合でなければならない)」不可視の名義尺度(単極球状体)との接点はありません。それは既にあらかじめ( εδ論法によって規定される)可算範囲の上限や下限の外側に追いやられているという前提で話が出発するのです。
イプシロンデルタ論法をわかりやすく丁寧に~関数の極限の定義~
それでは他同様、Wikipediaの記述から出発します。まずは間隔尺度(Interval Scale)の定義。
対象に割り振る数字は順序水準の性質を全て満たし、差が等しいことは間隔が等しいことを意味する。 測定値の対(pair)の差の比較は意味がある。 加減の演算にも意味がある。 尺度上のゼロ点は任意で負の値も使える。
例はカレンダーの日付がある。 値の比は意味がない。直接の乗除の演算全般も同様に意味はない。 差の比には意味がある。 代表値は最頻値、中央値あるいは算術平均で表す。算術平均が最も多くの情報を与えるかどうかは対象による。 間隔尺度で測定したデータを間隔データと呼ぶ。 摂氏または華氏で測る温度も間隔尺度である。
続いて比例尺度(Proportional Scale)の定義。
対象に割り振られた数字は間隔尺度の性質を全て満たし、さらにその中のペアの比にも、乗除の演算にも意味がある。比率水準のゼロ点は絶対的である。
ほとんどの物理学的量、つまり質量、長さやエネルギーは比率水準である。また温度も絶対温度で測れば比率尺度である。比率尺度で測定される変数の代表値は最頻値、中央値、算術平均あるいは幾何平均で表されるが、間隔尺度と同じく算術平均が最も多くの情報を与える。比率尺度で測定されるデータは比率データと呼ばれる。比率尺度で表される社会的変数には年齢、ある場所での居住期間、収入などといったものがある。
説明がゴチャゴチャしてるせいで定義が上手く頭に入ってきません。とにかく「比例尺度は物理学的量の観察結果に等しい」というのですから、そちらから再出発する事にしましょう。
ノーバート・ウィナー「サイバネティクス(1948年-1961年)」
電気回路の現象は、他の多くの物理的現象と同様に、時間の原点の移動に対して不変であるという特徴を有している。正午にある物理実験を開始して午後2時にある段階到達したとする。12時15分に同じ実験を開始すれば、2時15分にそれと同じ段階に到達するであろう。したがって物理学の法則は時間の並行移動の群を扱うのである。
それでは順番に見ていきましょう。
0次元テンソル(スカラー)と等差数列と等比数列を用いた計量可能空間の仮定義
①「1が無限に続く行列」$N_n$概念から出発する。
N_n=(…,N_{n-1}=1,N_n=1,N_{n+1}=1,…)
この行列の任意の範囲a,bの総和n(積分によって連続量となる)はある種の0次元テンソル(スカラー)となる。
【ディープラーニング入門】4つの例で学ぶスカラ、ベクトル
N_{ab}=\sum_{n=a}^bNn→\int_{n=a}^bN_ndn=b-a
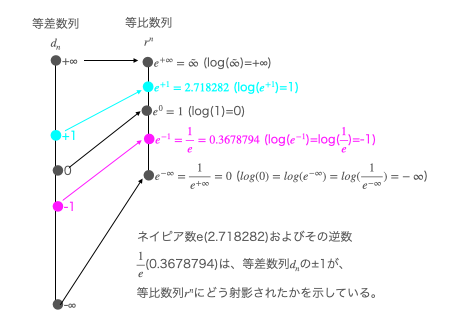
②今度はこのnを添字集合とする等差数列$d_n+C=d+d_{n-1}+C=d_{n+1}-d+C$(d=公比,C=初期値)…
d_n=(d_{-∞}=-∞,…,d_{n-1}+C,d_n+C,d_{n+1}+C,…,d_{+∞}=+∞)
および等比数列$r^n=r*r_{n-1}=\frac{r_{n+1}}{r}-α$(r=公比)を考える。
r^n=(r^{-∞}=\frac{1}{r^{+∞}}=0,…,r^{-1}=\frac{1}{r},r^0=1,r^{+1}=r,…,r^{+∞}=\tilde{∞})
③両者が重なるのは等差数列$d_n$が初期値d=1,公差0で等比数列$r^n$の公比が1の場合で、ここに①で当初示した「1が無限に続く行列」が復元される。
N_{ab}=\sum_{n=a}^bNn→\int_{n=a}^bN_ndn=b-a
ある種の循環論法ですが、これをここで用いる計量可能空間の出発点としたいと思います。
冪函数による統合と平行群概念への到達。
①上掲の等差数列$d_n+C$と等比数列$r^n$は、等差数列の初期値Cが0の場合においてのみ冪関数$r^d$(r=$r_0=1$を中心とする公比集合、d=$d_0=0$を中心とする交差集合)に統合される。
②ここに冪算の底の変換公式$α^x=e^{log(a)x}$を導入すると$r^d=e^{log(r)d}$となる。
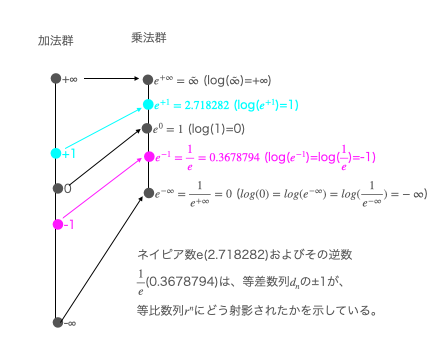
上掲の座標系に群概念を当てはめてみます。全体構造として無限小-∞から無限大+∞にかけての連続演算なので結合性(associativity)条件は自明の場合として満たされているとして「単位元eを中心に元gと(その元$g^{+1}$と掛け合わせると単位元eとなる)逆元$g^{-1}$が分布する」条件については…
-
等差数列$d_n$上の、$d_{-∞}=-∞$から$d_{+∞}=+∞$の範囲内で、かつその両端から可算可能範囲にない地点に単位元eを置くと、そこを中心に元$g^{+1}$と逆元$g^{-1}$ が分布する様になり、加法群の条件を満たす。
-
等差数列$r^n$上の、$r^{-∞}=0$から$r^{+∞}=\tilde{∞}$の範囲内で、かつその両端から可算可能範囲にない地点に単位元eを置くと、そこを中心に元$g^{+1}$と逆元$g^{-1}$ が分布する様になり、乗法群の条件を満たす。
ノーバート・ウィーナー「サイバネティクス」は、この様に「両端から可算可能範囲にない任意の地点に単位元eを置ける状態」を平行性と呼んだ訳です。なお等比数列$d_n$の初期値C≠0の場合も平行性自体は保たれるものの、この様な形での等比数列と等差数列の関係は失われてしまいます。
-
等比数列$d_n$と等差数列$r^n$が重なるのは等比数列$d_n$の初期値C=1の場合だけなのでここに矛盾が生じる。この矛盾を解消する為にも両数列の単位元を$r^{0}=1$で束ねる必要が出てくる。
-
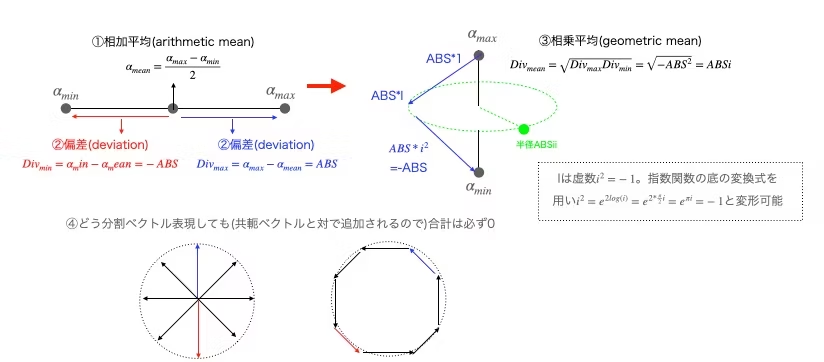
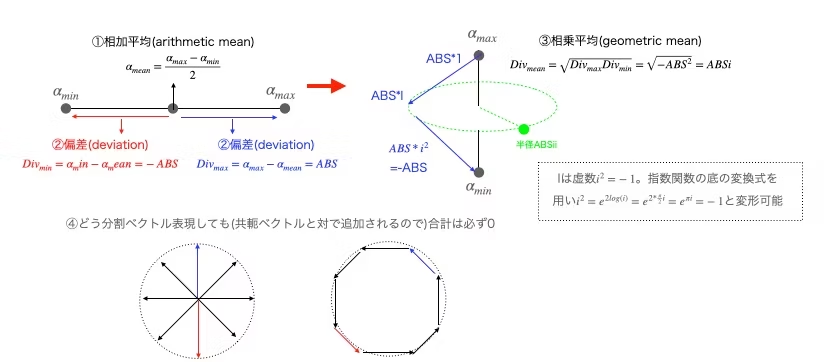
その一方で、かかる等差数列と等比数列の関係は任意の2値の相加平均(Arithmetic Mean)${\frac{a+b}{2}}$と相乗平均(Geometric mean)${\sqrt{ab}}$からから構成される複素円筒座標系に射影可能であり、その結果到達するのはオイラーの公式$e^{Θi}=cos(θ)+sin(θ)i$に基づく複素極座標系となる。
-
ノーバート・ウィーナー「サイバネティクス」もこの平行群については言及しており、関数族$e^{Θi}$と関数族$cos(θ)+sin(θ)i$それぞれの平行性を計算によって証明している。時間概念を持ち込む為に$θ=ωt$(ω=周期$\frac{t}{2π},t=時間$)として元時間τを起点に考えると…
e^{iω(τ+t)}=e^{iωτ}e^{iωt}
a cos(n(τ+t))+b sin(n(τ+t)))
=(a cos(nτ)+b sin(nτ))cos(nt)+(b cos(nτ)-a sin(nτ))sin(nt)
=a_1 cos(nt)+b_1 sin(nt)
- ノーバート・ウィーナー「サイバネティクス」はさらにこの平行群の線形性について言及する。
Ae^{iwt}+Be^{iwt}=(A+B)e^{iwt}
- この様な性質は原点を通る一次関数f(x)=pxなどだけでなく…
高校数学における線形性の8つの例
f(ax+by)=p(ax+by)
=a(px)+b(py)=af(x)+bf(y)
- 膨大な数(典型的にはアボガドロ数$10^{23}$程度)の粒子により構成される力学系たる統計力学(Statistical Mechanics)が扱うランダムウォーク(Random Walk)も備えているという。
Wikipedia「統計力学(Statistical Mechanics)」
ランダムウォークでは、一定時間での粒子の変位は、その時間の長さだけで定まり、その運動の開始時点以前のあらゆるできごとに無関係な確率分布をもっている。そのようなランダムウォーク全体に時間の並行移動を施せば、同じ集合に移るのである。
この特徴は統計学の対象全体に一般化出来るのでは? というより、そもそも対象にそうある事を期待する統計学を物理学の世界に射影した結果生まれたのが統計力学なる分野なのでは?
確率密度空間と累積分布空間①記述統計との狭間
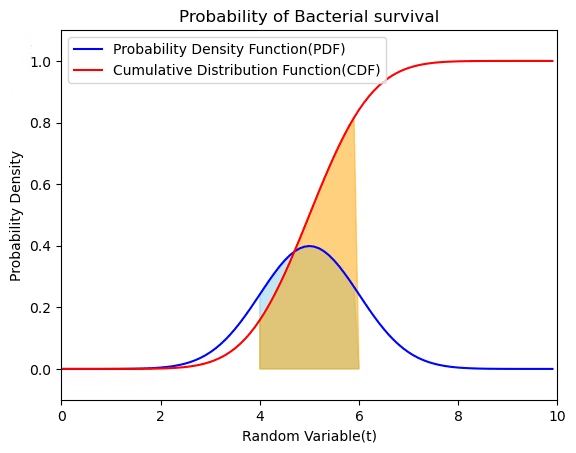
実際、線形性を備えているのは統計分野からですね。例えば期待値Eについて…
和の期待値は期待値の和【期待値の線形性】
E(aX+bY)=aE(X)+bE(Y)
そこまではいいとして、どことなく「エルゴード仮説についてのデリケートな話題」に踏み込んでしまった気も。なおChatGPTに「エルゴード仮説について説明してください」と投げたら、こんな答えが返ってきました。
エルゴード仮説は、マルコフ連鎖の性質に関する仮説です。マルコフ連鎖は、過去の状態に依存せずに次の状態が決定される確率過程を表します。エルゴード仮説は、このようなマルコフ連鎖がある条件を満たす場合に、その連鎖が「エルゴード」と呼ばれる特性を持つことを述べています。
具体的には、エルゴード仮説は以下の2つの条件を指摘しています:
- 状態空間内のあらゆる状態が、有限な時間内に他の任意の状態に到達する可能性があること。
- 長期間の平均が、状態の確率分布に収束すること。
この仮説は、マルコフ連鎖が十分な条件を満たす場合、適切なサンプリング手法とともに、確率的なシミュレーションやモンテカルロ法などの応用において、収束性や均衡状態の理論的保証を提供します。
まさかコンピューター・シミュレーション結果を証拠になんの躊躇いもなく全面肯定してくるとはねぇ…
【初心者向け】「モンテカルロ法」概説

実際、この考え方がただのハルシネーションではないのが恐ろしいところ…
マルコフ連鎖モンテカルロ法のエルゴード性についての解析
その一方でこんな話も。
MCMCが上手くいく時といかない時
こうして全体像を俯瞰してみると以下の様な全体像が浮かび上がってくる訳です。
- 上掲の条件を全て備えてるのが比例尺度(Proportional Scale)。
- 等差数列$d_n$の初期値Cが0と想定出来ない状況に適用されるのが間隔尺度(Interval Scale)。
- リサーチで得られる計測データ$X_n$の多くは、かかる厳密な定義においては間隔尺度条件しか満たさないが、平均$\bar{X}=\frac{\sum_{n=1}^NX_n}{N}$を求め、それを引いた偏差$X_n-\bar{X}$を用いる事で「近似的に比例尺度を満たした」と考える。
逆をいえば、物理現象の観測と異なり「近似的に比例尺度を満たしている」だけなので「平均の違い」に意味がある場合があり、それを調べる為にt検定や分散分析(ANOVA)の様な分析技法が開発されたとも。
Wikipedia「t検定」
Wikipedia「分散分析(ANOVA=ANalysis Of VAriance)」
なるほど、厳密に考えていくとこんな展開に。そんな感じで以下続報…