はじめに
千葉大学/Nospareの米倉です.今回はベイズ統計学でよく使われる,マルコフ連鎖モンテカルロ法(MCMC)が上手行く時・いかない時はどんな状況なのかを確認したいと思います.簡単化のために,ランダム・ウォーク・メトロポリス法を特に扱います.
ランダム・ウォーク・メトロポリス法(RWM)
話に入る前に,最も簡単なMCMCの一つであるランダム・ウォーク・メトロポリス法(RWM)について確認します.
今,$\pi()$をターゲットとなる密度関数だとします.現在のポジション$x$を所与として,次のポジションの候補となる$y$を,$q(y\mid x)=q(x\mid y)$を満たす条件付き密度関数からサンプリングします.典型例は$q(y\mid x)=x+\epsilon$で,ここで$\epsilon$は$x$とは独立で同一な正規分布に従う確率変数です.
次にメトロポリス・ヘイスティング比$\alpha(y,x)=\frac{\pi(y)q(y\mid x)}{\pi(x)q(x\mid y)}=\frac{\pi(y)}{\pi(x)}$を計算します.
最後に$u$を区間$(0,1)$の一様分布からサンプリングし,$u$が$\alpha(y,x)$より大きかったら候補となった$y$を棄却して,$y=x$とします.逆に小さかったら採択して,$y=y$とします.
上の3個のステップを任意の$M$回繰り返すのが,RWMです.
RWMが上手くいく条件
MCMCが上手くいく条件を「エルゴード性」といいます.MCMCの文脈におけるエルゴード性とは,平たく言うと,どんな初期分布からMCMCを始めても,ある程度の速さで発生させた乱数が事後分布に収束することをいいます.なので,MCMCのアルゴリズムがエルゴード的か否かが,数学的にそのMCMCが上手くいくかいかないかを保証するものとなります.
RWMの場合,RWMがエルゴード性を持つための「十分条件」はターゲットとなる分布の形に依存します.簡単化のためにターゲット$\pi()$は1次元の密度関数としましょう.この時,ある$x_{0}>0$と$a>0$と任意の$y\geq x\geq x_{0}$について,$$\frac{\pi(y)}{\pi(x)}\leq \exp(-a(y-x))$$と,同様に任意の$y\leq x\leq -x_{0}$に対して$$\frac{\pi(y)}{\pi(x)}\leq \exp(-a(x-y))$$が成立すると,RWMはエルゴード的(正しくは幾何エルゴード的)になることが知られています.
これはRWMがエルゴード性を持つためには,ターゲットとなる密度関数$\pi(x)$の裾は指数関数的に小さくなっていくことを要求していて,例えばコーシー分布の様に裾が厚い分布に対しては,RWMはエルゴード的にならないことを意味しています.詳しくは K. L. Mengersen and R. L. Tweedie (1996)を例えば参照してみてください.
数値実験
数学的なことをみてきたので,最後に数値実験を通して理論が意味することを確認したいと思います.まずターゲットとして,$\pi(x)\propto \exp(-x^{2}/2)$と言う,標準正規分布に比例する密度を考えます.下の結果は異なる初期値$x_{0}=50,0$からRWMを用いてサンプリングを行った結果です.プロポーサル密度には標準正規分布を用いました.図から分かる通り,どんなに外れた点(分布の裾)から初めても$0$付近にきちんと収束することが分かります.このことは発生させたサンプルのヒストグラムと標準正規分布の密度関数を重ね合わせても,きちんと動いていることが分かります.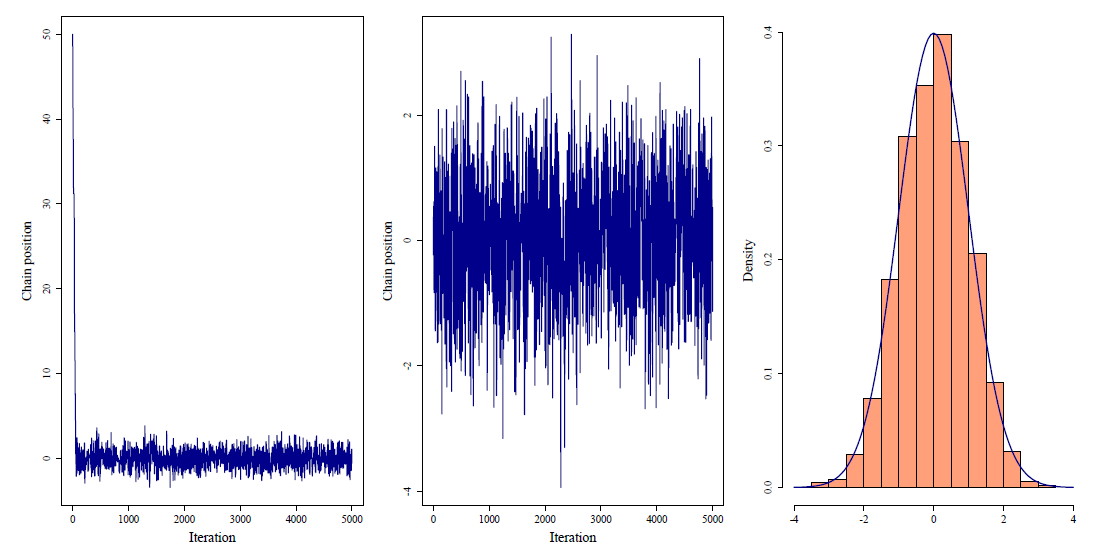
次にターゲットを$\pi(x)\propto \frac{1}{1+\mid x \mid^{1.1}}$と言う,コーシー分布っぽい裾の厚い分布に比例するものを考えて,先ほどと同じようにRWMを用いてサンプリングを行います.そうすると,先ほどとは対照的に発生させた乱数はランダムウォークの様なふるまいをみせて,全く収束しないことが分かります.ヒストグラムと密度関数を重ねても,全く動いていなことが分かります.

おわりに
ベイズ推定を行う際にMCMCを用いてサンプリングを行うことが非常に多いと思いますが,上手くいく・いかないはターゲットの形状と用いるMCMCの種類に依存します.やみくもに用いるのではなく,データをプロットして形状を把握したり,適切なMCMCサンプラーを用いるための(高度な)知識が必要不可欠です.株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.
