title: 評価行列とアイテムの説明文書を活用した推薦システム「ConvMF」を何とか実装していきたい!④ConvMFにおけるCNNパートの実装
参考
- 元論文
- nishiba様のConvMF実装例(Chainerをお使いになってました!)
- 自然言語処理におけるEmbeddingの方法一覧とサンプルコード
- けんごのお屋敷 様の記事
はじめに
KaggleのPersonalized Recommendationコンペに参加して以降、推薦システムが自分の中で熱くなっております。以前、Implicit Feedbackに対するモデルベースの協調フィルタリング(Matrix Factorization)の論文を読んで実装してみて、今度は更に実用的(?)で発展的な手法を触ってみたいと思い、「Convolutional Matrix Factorization for Document Context-Aware Recommendation」を読みました。この論文では、Matrix Factorizationによるモデルベース協調フィルタリングに、CNNを用いてアイテムの説明文書の情報を組み合わせる ConvMF(Convolutional Matrix Factorization)を提案しています。
今実装中ですが、なかなかPytorchと仲良くなれず、苦戦しております...。(ちなみに元論文はKerasで実装しておりました!)
パート4とした本記事では、前回のパート3(NLPにおけるCNNの活用を学ぶ)を参考に、ConvMFにおけるCNNパートの実装についてまとめています。**アイテムjの説明文書$X_j$を受け取って、document latent vector $s_j$を出力する$CNN(W, X_j)$**の事ですね:)
本記事以前のパートは、以下のリンクを御覧ください。
- 評価行列とアイテムの説明文書を活用した推薦システム「ConvMF」を何とか実装していきたい!①MFパートの実装
- 評価行列とアイテムの説明文書を活用した推薦システム「ConvMF」を何とか実装していきたい!②MFパートの実装
- 評価行列とアイテムの説明文書を活用した推薦システム「ConvMF」を何とか実装していきたい!③自然言語処理におけるCNN. テキスト分類を実装してみる
前回のリマインド
ConvMF(畳み込み行列分解)とは?
Convolutional Matrix Factorization(通称ConvMF)は、モデルベース協調フィルタリングにおいて評価行列のスパース性の上昇問題やコールドスタート問題に対応する為に提案された、Explicit FeedbackやImplicit Feedbackの評価情報に加えてアイテムの説明文書(ex. ニュース記事の中身、動画のタイトル、etc.)の情報を考慮した推薦手法の一つです。
その為に、ConvMFではモデルベース協調フィルタリングであるPMF(Probabilistic Matrix Factorization)にCNN(convolutional neural network)を統合しています。
その結果、ConvMFは最終的に協調情報と文脈情報の両方を効果的に利用することができ、評価データが極めて疎な場合でも、ConvMFは未知の評価を正確に予測することができる、らしいです...。
ConvMFの確率モデル
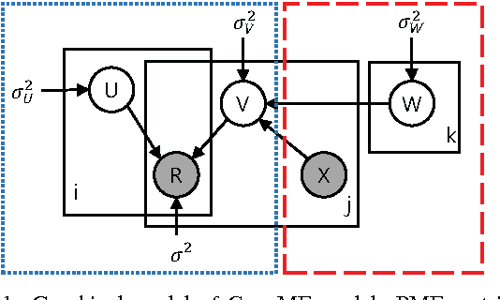
以下の図は、NLPに対するCNNモデルをPMF(確率的行列分解)モデルに統合した、ConvMFの確率モデルの概要を示したモノになります。
ちなみに上図において、各記号の意味合いは以下です。(順次まとめていきます)
- $U$: user latent model
- $V$: item latent model
- $R$: Rating Matrix
- $X$: アイテムのDescription(説明文)
- $W$: CNNのパラメータ達。
- $i, j$: それぞれ、各ユーザと各アイテムを表す添字。
- $k$:CNN内の各パラメータを表す添字(kに関しては、潜在ファクターの次元数の記号と混在してるかもしれません...?)
また問題設定として、N人のユーザとM個のアイテムがあり、観測された評価行列は$R\in \mathbb{R}^{N\times M}$行列で表現されるとします。
そして、その積($U^T \cdot V$)が評価行列 $R$を再構成するような、ユーザとアイテムの潜在モデル($U\in \mathbb{R}^{k\times N}$ と $V \in \mathbb{R}^{k\times M}$)を見つけることが目的になります。
特にConvMFでは、アイテムjの説明文書ベクトル$X_j$を考慮して$V_j$を推定する点が大きな特徴になります。
ConvMFにおけるパラメータ推定法
ConvMFでは、パラメータ($U, V, W$)を最適化する為に、MAP推定(maximum a posteriori estimation)を行います。
事後分布の式を対数化してマイナスを掛け、いい感じに変形($\sigma^2$で割る!)と、以下のようになりますね(前パート参照)。
$$
L(U,V,W|R, X, \lambda_U, \lambda_V, \lambda_W)
= \frac{1}{2} \sum_{i}^N \sum_{j}^M I_{ij}(r_{ij} - u_{i}^T v_j)^2 \
- \frac{\lambda_U}{2} \sum_{i}^N||u_i||^2 \
- \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \
- \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2
\
(
\lambda_U = \frac{\sigma^2}{\sigma_U^2},
\lambda_V = \frac{\sigma^2}{\sigma_V^2},
\lambda_W = \frac{\sigma}{\sigma_W^2}
)
$$
この式を最小化するような$U, V, W$を求めるわけです。
ConvMFの学習では、UとVとWの内2つを固定して、一つずつ最適化していく、Alternating Least Square(ALS)的なアプローチを取っていきます。
user latent matrix $U$とitem latent matrix $V$ の推定方法に関しては、ALS同様に、閉形式(closed-form, 要するに解析的に解ける式?)で解析的に計算することができます。
$$
u_i \leftarrow (V I_i V^T + \lambda_U I_K)^{-1}VR_i \tag{7}
$$
$$
v_j \leftarrow (U I_j U^T + \lambda_V I_K)^{-1}(UR_j + \lambda_V \cdot cnn(W, X_j)) \tag{8}
$$
$V$に関しては、$\lambda_V \cdot cnn(W, X_j)$が含まれているのが、通常のMFとの大きな違いであり、ConvMFの特徴ですね。
ここで
- ユーザiについて
- $I_i$ は$I_{ij} , (j=1, \cdots, M)$を対角要素とする対角行列。
- $R_i$ はユーザiについて$(r_{ij})_{j=1}^M$とするベクトル。
- つまり、ユーザiの各アイテムjに対する評価値が入ったベクトル!
- アイテムjについて
- $I_j$と$R_j$の定義は、$I_i$と$R_i$のものと同様。
- 式(8)はアイテム潜在ベクトル$v_j$を生成する際のCNNのDocument潜在ベクトル$s_j = cnn(W, X_j)$の効果を示している。
- $\lambda_V$はバランシングパラメータ(要は重み付け平均みたいな?, 意味合いとしては正則化項のハイパラ?)になる。
CNN内のパラメータWの推定方法に関しても、UとVを定数と仮定してWを推定する方針は同じです。以下の損失関数を最小化するようなパラメータ$W$を求めていきます。
\varepsilon(W) = \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \\
+ \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2 + constant \tag{9}
最終的には、最適化された$U, V, W$により、「アイテム$j$に対するユーザ$i$の未知の評価 $r_{ij}$」を推定する事ができます。
r_{ij} \approx E[r_{ij}|u_i^T v_j, \sigma^2] \\
= u_i^T v_j = u_i^T \cdot (cnn(W, X_j) + \epsilon_j)
\tag{10}
ここまでで、簡単なConvMFの理論の復習は完了です。
$s_j = CNN(W, X_j)$についての詳細な説明
ConvMFにおけるCNNアーキテクチャの目的は、アイテムのdocuments(文書)からdocument latent vectors(文書潜在ベクトル)を生成し、それと撹乱項($\epsilon$)を用いてitem latent models(アイテム特徴行列)を構成する事です。
上の図はConvMFで用いられるCNNアーキテクチャを示しており、
- 1)Embedding layer
- 2)Convolution layer
- 3)Pooling layer
- 4)Output layer
の4層から構成されています。
Embedding Layer(埋め込み層)
Embedding layerでは、生のDocumentを、次のConvolution layerへ入力する準備として、Documentを表す密な数値行列に変換します。
- 具体的には、Documentを$l$個の単語の列と見なし、Document中の各単語のベクトルを連結して行列として表現する。(場合によっては、各"文字"を最小単位として扱う事もありうる??)
- 単語ベクトルはランダムに初期化されるか、事前に学習された単語埋め込みモデルで初期化される。(ex. Word2Vec??)
- この単語ベクトルは、さらに最適化処理によって学習される。
そしてこの場合、ある一つのDocumentのDocument Matrix$D \in \mathbb{R}^{p \times l}$は次のようになります。
$$
D_j = [
\begin{array}{cc}
& | & | & | & \
\cdots & w_{i-1} & w_{i} & w_{i+1} & \cdots \
& | & | & | & \
\end{array}
] = \text{embedding layer}(X_j)
$$
ここで
- $l$:Documentの長さ(最小単位が"単語"の場合、単語数)
- $p$:各単語ベクトル$w_i$の埋め込み次元の大きさ
- $D_j$:アイテムjのDocument $X_j$を変換して得られたDocument Matrix
Convolution Layer 畳み込み層
Convolution LayerはDocument Matrix $D_j$から文書の特徴を抽出します。
一般にCNNはコンピュータビジョンの分野で多く活用されますが、自然言語に対しても使われます。
画像データに対するCNNとは異なり、自然言語に対するCNNでは、Kernel(i.e. スライド窓関数, filter, feature detector)の幅が、Document Matrixの幅と合致します。
つまり本記事においては、Kernelの幅は「各単語ベクトル$w_i$の埋め込み次元の大きさ$p$」と合致する、という事ですね。
Kernelの高さに関しては、元論文では[3, 4, 5]の三種類を使用しており、本記事でもそれに従って実装します。
k番目のConvolution layerから得られる document feature $c_{i}^{k}$は、k番目のShared Weight$W_{c}^{k} \in \mathbb{R}^{p\times ws}$(=これがKernel!) によって特徴抽出されます。
$$
c_i^k \in \mathbb{R}= f(W_c^k * D_{(:, i:(i+ws -1))} + b_c^k)
$$
ここで、各記号は以下の意味です。
- $i$はDocument Matrix中の各単語ベクトルを表す添字。
- $k$はk番目のShared Weight(=カーネル??)を表す添字。
- $c_i^k$: ある任意のDocument Matrix $D_j$において、i番目の単語ベクトル周辺をk番目のShared Weight(=カーネル??)によって畳み込んで得られた実数値。
- $*$は畳み込み演算子(Convolution operator)
- Document Matrixの一部にKernelが要素毎に掛け合わされ、それらの和が計算されたのが $W_c^k * D_{(:, i:(i+ws -1))}$
- つまり、アダマール積の和をとってるって事ですね!
- $b_c^k$は$W_c^k$のバイアス。
- つまり、アダマール積の和に足される定数項ですね!
- $f$は非線形活性化関数(non-linear activation function)
- シグモイド、tanh、rectified linear unit (ReLU)などの非線形活性化関数のうち、最適化の収束が遅く、局所最小値が悪くなる可能性のあるvanish gradientの問題を避けるためにReLUを用いる
プーリング層
hoge
全結合層
hogehoge
ConvMFにおける CNNパート ($s_j = CNN(W, X_j)$)を実装してみる。
では実装に入ります。基本的にはパート3のCNNによるテキスト分類の実装をアレンジしています。nn.Moduleクラスを継承しCnnNlpModelクラスとして実装していきます。
from typing import List, Optional, Tuple
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch import Tensor
class CnnNlpModel(nn.Module):
# hogehoge
コンストラクタ
まずはコンストラクタで、モデルの各層(埋め込み層、畳み込み層、全結合層)を定義していきます。3つのprivateメソッドを呼び出し、各層をインスタンス変数として保存していきます。
class CnnNlpModel(nn.Module):
"""ConvMFにおける CNNパート ($s_j = CNN(W, X_j)$)を実装する為のクラス"""
def __init__(
self,
output_dimension: int,
pretrained_embedding: Optional[torch.Tensor] = None,
freeze_embedding: bool = False,
vocab_size: Optional[int] = None,
embed_dimension: int = 300,
kernel_sizes: List[int] = [3, 4, 5],
num_kernels: List[int] = [100, 100, 100],
dropout_ratio: float = 0.5,
) -> None:
"""
Args:
output_dimension (int): Number of classes.
最終的なCNNの出力次元数。
目的変数の次元数(ConvMFの場合はこれがItem Latent Vectorの次元数になる)
pretrained_embedding (torch.Tensor): Pretrained embeddings with
shape (vocab_size, embed_dim). 学習済みの単語埋め込みベクトル。
freeze_embedding (bool): Set to False to fine-tune pretraiend
vectors. 学習済みの単語埋め込みベクトルをfine-tuningするか否か。
Default: False
vocab_size (int): vocabrary size. Need to be specified when not pretrained word
embeddings are not used. 学習済みの単語埋め込みベクトルが渡されない場合、指定する必要がある。
embed_dim (int): Dimension of word vectors. Word Vectorの次元数。
Need to be specified when pretrained word embeddings are not used.
学習済みの単語埋め込みベクトルが渡されない場合、指定する必要がある。
Default: 300
kernel_sizes (List[int]): List of filter sizes.
畳み込み層のスライド窓関数(カーネル)のwindow size(高さのみ。幅はw_iの埋め込み次元の大きさ)を指定する。
Default: [3, 4, 5]
num_filters (List[int]): List of number of filters, has the same
length as `filter_sizes`.
畳み込み層のスライド窓関数(Shared weihgt)の数
Default: [100, 100, 100]
dropout_ratio (float): Dropout rate.
中間層のいくつかのニューロンを一定確率でランダムに選択し非活性化する。
Default: 0.5
"""
super(CnnNlpModel, self).__init__()
self.embedding_layer, self.embed_dim = self._define_embedding_layer(
pretrained_embedding,
freeze_embedding,
embed_dimension,
vocab_size,
)
self.conv1d_layers = self._define_conv_layers(
input_dim=self.embed_dim,
num_filters=num_kernels,
filter_sizes=kernel_sizes,
)
self.fc_layer1, self.fc_layer2 = self._define_fc_layers(
input_dim=np.sum(num_kernels),
output_dim=output_dimension,
)
self.dropout = nn.Dropout(p=dropout_ratio)
埋め込み層の定義
まず_define_embedding_layer()メソッドで、各単語(token)をベクトルに変換する為の埋め込み層(embedding layer)を定義します。
学習済み単語ベクトルが引数に渡されている場合はそれを使用して、渡されない場合は畳み込みベクトルの次元数(embed_dimension)と畳み込み層に登録される単語数(vocab_size)を用いて、nn.Embeddingオブジェクトを生成して返します。
def _define_embedding_layer(
self,
pretrained_embedding: Optional[torch.Tensor] = None,
freeze_embedding: bool = False,
embed_dimension: Optional[int] = None,
vocab_size: Optional[int] = None,
) -> Tuple[nn.Embedding, int]:
"""Embedding layer(埋め込み層)の定義
- 学習済みの単語埋め込みベクトルの配列が指定されない場合、embed_dimensionとvocab_sizeに基づき単語埋め込みベクトルを初期化
- 指定された場合、pretrained_embedding_vectorsに基づき、nn.Embeddingを生成
Return
Tuple[embedding_layer,embed_dimension]
"""
if pretrained_embedding is None:
embedding_layer = nn.Embedding(
num_embeddings=vocab_size, # 語彙サイズ
embedding_dim=embed_dimension, # 埋め込みベクトルの次元数
padding_idx=0, # 文章データ(系列データ)の長さの統一:ゼロパディング
max_norm=5.0, # 単語埋め込みベクトルのnorm(長さ?)の最大値の指定。これを超える単語ベクトルはnorm=max_normとなるように正規化される?
)
else:
vocab_size, embed_dimension = pretrained_embedding.shape
embedding_layer = nn.Embedding.from_pretrained(
pretrained_embedding,
freeze=freeze_embedding,
)
return embedding_layer, embed_dimension
畳み込み層の定義
_define_conv_layers()メソッドで、畳み込み層を定義します。
kernel_sizeの種類分の繰り返し処理の中で、入力次元数=埋め込みベクトルの次元数,出力次元数=kernelの数で、一次元の畳み込み層nn.Conv1dオブジェクトを作ります。各Kernelサイズのnn.Conv1dをListにまとめて、nn.ModuleListにして返します。
def _define_conv_layers(
self,
input_dim: int,
num_kernels: List[int],
kernel_sizes: List[int],
) -> nn.ModuleList:
"""Conv Layersの定義
スライド窓関数のwindow size(resign size)の種類分の繰り返し処理で,
一次元の畳み込み層を定義していく.
"""
modules = []
for filter_size, num_filter in zip(kernel_sizes, num_kernels):
conv_layer = nn.Conv1d(
in_channels=input_dim, # 入力チャネル数:埋め込みベクトルの次元数
out_channels=num_filter, # 出力チャネル数(pooling後、resign size毎に代表値を縦にくっつける)
kernel_size=filter_size, # window size(resign size)(Conv1dなので高さのみ指定)
padding=0, # ゼロパディング
stride=1, # ストライド
)
modules.append(conv_layer)
return nn.ModuleList(modules=modules)
全結合層の定義
_define_fc_layers()メソッドで全結合層 を定義します。
入力次元数はカーネル数の合計(np.sum(num_kernels))、出力次元数はItem latent vectorの次元数として、隠れ層1つの全結合層
def _define_fc_layers(
self,
input_dim: int,
output_dim: int,
) -> Tuple[nn.Linear, nn.Linear]:
"""Fully-connected layer and Dropout 全結層を定義する
- 入力d_f(次元数はR^{n_c}), 出力はs_j(次元数はR^{n_factor})
- バイアス項あり。活性化関数は2回ともtanh.
"""
hidden_dim = input_dim * 2
fc1 = nn.Linear(in_features=input_dim, out_features=hidden_dim)
fc2 = nn.Linear(in_features=hidden_dim, out_features=output_dim)
return fc1, fc2
forward()メソッド()を実装
続いて、forward()メソッド(モデルが入力データを受け取り、出力データを生成する処理)を定義していきます。
以下のような処理を実装しています。
- 想定される入力値:batch_size個のtokenized text
- Input shape:
(batch_size, length_of_sentence)
- Input shape:
- まずEmbedding層にtokenize(符号化)されたtextを渡して、文書行列(x_embed)を取得する
- -> Output shape:
(batch_size, length_of_sentence, embed_dim)
- -> Output shape:
- 続いて、Tensorの軸の順番を入れ替えて、Tensor.shapeを畳み込み層の入力用に整形する. (batch_size, length_of_sentence, embed_dim)=>(batch_size, embed_dim, length_of_sentence)
- -> Output shape:
(batch_size, embed_dim, length_of_sentence)
- -> Output shape:
- 続いて、畳み込み層 及び 活性化関数(ReLU)を適用する.
- ->Output shape:
List[batch_size, num_filters[i], convolutionの出力数]
- ->Output shape:
- 続いて、各convolutionの出力値にmax poolingを適用して、代表値を取得する.
- ->Output shape:
List[(batch_size, num_filters[i], 1)]
- ->Output shape:
- 続いて、x_pool_listを連結して、fully connected layerに投入する為のshapeに変換
- ->Output shape:
(batch_size, sum(num_filters))
- ->Output shape:
- 最後に、全結合層に入力。batch_size個のdim_output次元ベクトルを得る。入力->中間 & 中間->出力の活性化関数はどちらもTanhを使用しています。
- Output shape:
(batch_size, dim_output)
- Output shape:
def forward(self, input_token_indices: Tensor):
"""Perform a forward pass through the network.
Args:
input_ids (torch.Tensor): A tensor of token ids
with shape (batch_size, length_of_sentence)
Returns:
torch.Tensor: Output tensors with shape (batch_size, dim_output)
"""
x_embed: Tensor = self.embedding_layer(input_token_indices).float()
# -> Output shape: (batch_size, length_of_sentence, embed_dim)
x_reshaped = x_embed.permute(0, 2, 1)
# -> Output shape: (batch_size, embed_dim, length_of_sentence)
x_conv_list = [F.relu(conv1d(x_reshaped)) for conv1d in self.conv1d_layers]
# ->Output shape: List[batch_size, num_filters[i], convolutionの出力数]
x_pool_list: List[Tensor] = [F.max_pool1d(x_conv, kernel_size=x_conv.shape[2]) for x_conv in x_conv_list]
# ->Output shape: List[(batch_size, num_filters[i], 1)]
x_squeezed_for_fc = torch.cat([x_pool.squeeze(dim=2) for x_pool in x_pool_list], dim=1)
# ->Output shape: (batch_size, sum(num_filters))
x_fc1 = torch.tanh(self.fc_layer1(x_squeezed_for_fc))
# -> Output shape: (batch_size, dim_hidden)
x_fc2 = torch.tanh(self.fc_layer2(x_fc1))
# -> Output shape: (batch_size, dim_output)
return x_fc2
forwardの動作確認
if __name__ == "__main__":
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
cnn_nlp_model = CnnNlpModel(
output_dimension=10,
vocab_size=100,
embed_dimension=15,
)
# 入力データ(tokenized text 2つを想定)
x = torch.Tensor(
[
[0, 1, 2, 3, 4, 5],
[2, 1, 3, 4, 5, 0],
]
).long() # LongTensor型に変換する(default はFloatTensor?)
print(x)
y = cnn_nlp_model(x)
結果として以下が出力されました。tokenized textを受け取って、output_dimension次元のベクトルを出力しています。とりあえずコンストラクタ及びforward()メソッドは想定通りに実装できていそうです:)
tensor([[0, 1, 2, 3, 4, 5],
[2, 1, 3, 4, 5, 0]])
tensor([[-0.0347, 0.3333, 0.0967, 0.1088, -0.0563, -0.1277, 0.2418, -0.3997,
-0.2026, -0.0588],
[ 0.0108, 0.3249, 0.0640, 0.0233, -0.0772, 0.0985, 0.3312, -0.1932,
-0.2195, -0.2146]], grad_fn=<TanhBackward>)
自作損失関数の定義
ConvMFのCNNパートの学習に用いる損失関数$\varepsilon(W)$は以下の通りです。
(交互最小二乗法に基づき、U(user latent matrix)とV(item latent matrix)を一時的に定数と仮定する事で、ConvMF全体の損失関数$L$(詳しくはパート1参照)を「$W$に関してL2正則化項を持つ二乗誤差関数」として解釈しています...!)
\varepsilon(W) = \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \\
+ \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2 + constant
\tag{9}
ここで、
- W: NlpCnnModelで推定すべきパラメータ群
- j: 各アイテムを表す添字
- $w_k$: Wにおいてk番目のパラメータ。
- $v_j$: アイテムjに関するitem latent vector
- $X_j$: アイテムjに関する説明文書のtokenizeされたテキスト
- $\lambda_V$及び$\lambda_W$は損失関数におけるバランシングパラメータ(要は重み付け平均みたいな?, 意味合いとしては正則化項のハイパーパラメータ)
- 右辺第一項がWに関する二乗誤差関数。
- 右辺第二項がWにとってのL2正則化項とみなせる。
Pytorchに既存で用意されている損失関数クラス達には含まれていないので、上の数式の損失関数クラスを自作してみます。
from typing import Iterator, List
import torch
import torch.nn as nn
from torch import Tensor
from src.model.cnn_nlp_model import CnnNlpModel
class ConvMFLossFunc(nn.Module):
def __init__(self, lambda_v: float, lambda_w: float) -> None:
super().__init__()
self.lambda_v = lambda_v
self.lambda_w = lambda_w
def forward(
self,
outputs: Tensor,
targets: Tensor,
parameters: Iterator[nn.Parameter],
) -> torch.Tensor:
"""
outputs: 予測結果(ネットワークの出力)
targets: 正解
parameters: CNNモデルのパラメータ
"""
# 右辺第一項(Wに関する二乗誤差関数)
loss = (self.lambda_v / 2) * ((targets - outputs) ** 2).sum()
# 右辺第二項(WにとってのL2正則化項)を右辺第一項に加える
l2 = torch.tensor(0.0, requires_grad=True)
for w in parameters:
l2 = l2 + torch.norm(w) ** 2
loss = loss + (self.lambda_w / 2) * l2
return loss
入力値と出力値と推定対象のパラメータを用意して、軽く動作確認してみます。
if __name__ == "__main__":
cnn_nlp_model = CnnNlpModel(
output_dimension=10,
vocab_size=100,
embed_dimension=15,
)
loss_function = ConvMFLossFunc(lambda_v=0.01, lambda_w=0.1)
# 実際の値(item latent vector)
y_true = torch.Tensor(
[
[2.0, 1.3, 0.1],
[4.0, 1.2, 4.1],
]
)
# 予測値(NlpCnnModelの出力)
y_pred = torch.Tensor(
[
[1.5, 1.2, 0.4],
[3.0, 2.0, 3.1],
]
)
# 実際の値と予測値の差を計算する
loss = loss_function(y_true, y_pred, cnn_nlp_model.parameters())
print(loss)
結果として以下が出力されました。想定通りに動作してくれていそうです。
tensor(93.1811, grad_fn=<AddBackward0>)
学習用の関数を作成する
さてモデルも損失関数も定義し終えたので、最後に学習用の関数を定義します。
モデルクラスのメソッドにすべきか関数として外に出すべきか迷った(今も迷っている...!)のですが、CNNによるテキスト分類の論文のコードに習い、とりあえずtrain()関数として定義しました。
train()の中身は、適用する損失関数とyのdtypeが違う事(分類ではLongTensor, 今回はFloatTensor)以外はpart3と同じです。
あとtrain()の中で呼ばれるprivate関数_evaluate()で、テキスト分類ではacuracyを計算していましたが、今回は損失関数の値のみを算出するようにしています。
def train(
model: CnnNlpModel,
optimizer: optim.Adadelta,
device: torch.device,
train_dataloader: DataLoader,
val_dataloader: Optional[DataLoader] = None,
epochs: int = 10,
):
"""Train the CNN_NLP model. 学習を終えたCNN_NLPオブジェクトを返す。
Parameters
----------
model : nn.Module
CNN_NLPオブジェクト。
optimizer : optim.Adadelta
Optimizer
device : torch.device
'cuda' or 'cpu'
train_dataloader : DataLoader
学習用のDataLoader
val_dataloader : DataLoader, optional
検証用のDataLoader, by default None
epochs : int, optional
epoch数, by default 10
Returns
-------
学習を終えたCNN_NLPオブジェクト
CnnNlpModel
"""
model.to(device) # modelをdeviceに渡す
# 損失関数の定義ConvMFLossFunc
loss_function = ConvMFLossFunc(lambda_v=0.01, lambda_w=0.1)
# Tracking best validation accuracy
print("Start training...\n")
for epoch_idx in range(epochs):
# =======================================
# Training
# =======================================
# Tracking time and loss
t0_epoch = time.time()
total_loss = 0
# Put the model into the training mode
model.train()
# バッチ学習
for batch_idx, batch_dataset in enumerate(train_dataloader):
batch_X, batch_y = tuple(tensors for tensors in batch_dataset)
# データをGPUにわたす。
batch_X: Tensor = batch_X.to(device)
batch_y: Tensor = batch_y.to(device)
# 1バッチ毎に勾配の値を初期化(累積してく仕組みだから...)
model.zero_grad()
# Perform a forward pass. This will return logits.
y_predicted = model(batch_X)
# 損失関数の値を計算
loss = loss_function(y_predicted, batch_y, parameters=model.parameters())
# 1 epoch全体の損失関数の値を評価する為に、1 batch毎の値を累積していく.
total_loss += loss.item()
# Update parameters(パラメータを更新)
loss.backward() # 誤差逆伝播で勾配を取得
optimizer.step() # 勾配を使ってパラメータ更新
# 1 epoch全体の損失関数の平均値を計算
avg_train_loss = total_loss / len(train_dataloader)
# =======================================
# Evaluation
# =======================================
# 1 epochの学習が終わる毎にEvaluation
if val_dataloader is None:
continue
# After the completion of each training epoch, measure the model's
# performance on our validation set.
val_loss = _evaluate(
model=model,
val_dataloader=val_dataloader,
device=device,
)
# Print performance over the entire training data
time_elapsed = time.time() - t0_epoch
print(f"the validation result of epoch {epoch_idx + 1:^7} is below.")
print(f"the values of loss function : train(average)={avg_train_loss:.6f}, valid={val_loss:.6f}")
print("\n")
print(f"Training complete!")
return model # 学習済みのモデルを返す
def _evaluate(
model: nn.Module,
val_dataloader: DataLoader,
device: torch.device,
) -> float:
"""After the completion of each training epoch, measure the model's
performance on our validation set.
"""
# 損失関数の定義
loss_fn = ConvMFLossFunc(lambda_v=0.01, lambda_w=0.1)
# Put the model into the evaluation mode. The dropout layers are disabled
# during the test time.
model.eval()
# Tracking variables
val_loss_list = []
# For each batch in our validation set...
for batch_datasets in val_dataloader:
batch_X, batch_y = tuple(tensors for tensors in batch_datasets)
# Load batch to GPU
batch_X: Tensor = batch_X.to(device)
batch_y: Tensor = batch_y.to(device)
# Compute logits
with torch.no_grad():
y_predicted = model(batch_X)
# Compute loss
loss: Tensor = loss_fn(y_predicted, batch_y, model.parameters())
val_loss_list.append(loss.item())
# Compute the average accuracy and loss over the validation set.
val_loss_mean = np.mean(val_loss_list)
return val_loss_mean
動作確認のため、適当なデータを使って実際に学習を回してみます。
if __name__ == "__main__":
# 入力データ
x = torch.Tensor(
[
[0, 1, 2, 3, 4, 5],
[2, 1, 3, 4, 5, 0],
]
).long() # LongTensor型に変換する(default はFloatTensor?)
y_true = torch.Tensor(
[
[0.5, 1.0, 2.0, 1.5, 1.8, 1.9, 1.0],
[0.8, 1.5, 2.1, 1.0, 1.0, 1.2, 1.8],
]
).float()
dataset = TensorDataset(x, y_true)
train_dataloader = DataLoader(dataset)
valid_dataloader = DataLoader(TensorDataset(x, y_true))
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
cnn_nlp_model = CnnNlpModel(
output_dimension=y_true.shape[1],
vocab_size=100,
embed_dimension=15,
)
optimizer = optim.Adadelta(
params=cnn_nlp_model.parameters(), # 最適化対象
lr=0.01, # parameter更新の学習率
rho=0.95, # 移動指数平均の係数
)
cnn_nlp_model_trained = train(
model=cnn_nlp_model,
optimizer=optimizer,
device=device,
train_dataloader=train_dataloader,
val_dataloader=valid_dataloader,
)
出力は以下のような感じです。Trainingデータがめちゃめちゃ適当なのでパターンも何もないのですが、上で自作した誤差関数がより小さくなるようにパラメータ群$W$を調整できている事がわかりますね...!よかったー笑
Start training...
the validation result of epoch 1 is below.
the values of loss function : train(average)=85.279125, valid=85.241795
the validation result of epoch 2 is below.
the values of loss function : train(average)=85.229351, valid=85.191574
the validation result of epoch 3 is below.
the values of loss function : train(average)=85.179058, valid=85.141155
the validation result of epoch 4 is below.
the values of loss function : train(average)=85.128559, valid=85.090332
the validation result of epoch 5 is below.
the values of loss function : train(average)=85.077721, valid=85.039513
the validation result of epoch 6 is below.
the values of loss function : train(average)=85.026878, valid=84.988697
the validation result of epoch 7 is below.
the values of loss function : train(average)=84.975925, valid=84.937614
the validation result of epoch 8 is below.
the values of loss function : train(average)=84.924858, valid=84.886562
the validation result of epoch 9 is below.
the values of loss function : train(average)=84.873852, valid=84.835445
the validation result of epoch 10 is below.
the values of loss function : train(average)=84.822731, valid=84.784382
Training complete!
終わりに
今回の記事では「Convolutional Matrix Factorization for Document Context-Aware Recommendation」の理解と実装のパート4として、ConvMFのCNNパートの実装をまとめました。今回の自作モデルなり自作損失関数なりの実装を通じて、Pytorchと少しだけ仲良くなれた気がします笑
次回はついに、パート2で実装したMatrixFactorizationクラスと今回実装したCnnNlpModelを用いて、"Ratingデータ"+"アイテムの説明文書"を活用した推薦アルゴリズムであるConvMFクラスを実装し、記事にまとめていきます...!!
そしてこの一連のConvMFの実装経験を通じて、"Ratingデータ"+"アイテムの説明文書"を活用した推薦システムについて実現イメージを得ると共に、"非常に疎な評価行列問題"や"コールドスタート問題"に対応し得る"頑健"な推薦システムについて理解を深めていきたいです。
理論や実装において、間違っている点や気になる点があれば、ぜひコメントにてアドバイスいただけますと嬉しいです:)