参考
- 元論文
- nishiba様のConvMF実装例(Chainerをお使いになってました!)
はじめに
KaggleのPersonalized Recommendationコンペに参加して以降、推薦システムが自分の中で熱くなっております。以前、Implicit Feedbackに対するモデルベースの協調フィルタリング(Matrix Factorization)の論文を読んで実装してみて、今度は更に実用的(?)で発展的な手法を触ってみたいと思い、「Convolutional Matrix Factorization for Document Context-Aware Recommendation」を読みました。この論文では、Matrix Factorizationによるモデルベース協調フィルタリングに、CNNを用いてアイテムの説明文書の情報を組み合わせる ConvMF(Convolutional Matrix Factorization)を提案しています。
今実装中ですが、なかなかPytorchと仲良くなれず、苦戦しております...。(ちなみに元論文はKerasで実装しておりました!)
パート2とした本記事では、ConvMFにおけるMatrix Factorizationパートの実装についてまとめています。
本記事以前のパートは、以下のリンクを御覧ください。
前回のリマインド
ConvMF(畳み込み行列分解)とは?
Convolutional Matrix Factorization(通称ConvMF)は、モデルベース協調フィルタリングにおいて評価行列のスパース性の上昇問題やコールドスタート問題に対応する為に提案された、Explicit FeedbackやImplicit Feedbackの評価情報に加えてアイテムの説明文書(ex. ニュース記事の中身、動画のタイトル、etc.)の情報を考慮した推薦手法の一つです。
その為に、ConvMFではモデルベース協調フィルタリングであるPMF(Probabilistic Matrix Factorization)にCNN(convolutional neural network)を統合しています。
その結果、ConvMFは最終的に協調情報と文脈情報の両方を効果的に利用することができ、評価データが極めて疎な場合でも、ConvMFは未知の評価を正確に予測することができる、らしいです...。
ConvMFの確率モデル
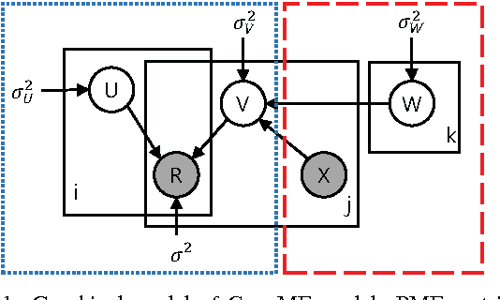
以下の図は、NLPに対するCNNモデルをPMF(確率的行列分解)モデルに統合した、ConvMFの確率モデルの概要を示したモノになります。
ちなみに上図において、各記号の意味合いは以下です。(順次まとめていきます)
- $U$: user latent model
- $V$: item latent model
- $R$: Rating Matrix
- $X$: アイテムのDescription(説明文)
- $W$: CNNのパラメータ達。
- $i, j$: それぞれ、各ユーザと各アイテムを表す添字。
- $k$:CNN内の各パラメータを表す添字(kに関しては、潜在ファクターの次元数の記号と混在してるかもしれません...?)
また問題設定として、N人のユーザとM個のアイテムがあり、観測された評価行列は$R\in \mathbb{R}^{N\times M}$行列で表現されるとします。
そして、その積($U^T \cdot V$)が評価行列 $R$を再構成するような、ユーザとアイテムの潜在モデル($U\in \mathbb{R}^{k\times N}$ と $V \in \mathbb{R}^{k\times M}$)を見つけることが目的になります。
特にConvMFでは、アイテムjの説明文書ベクトル$X_j$を考慮して$V_j$をを推定する点が大きな特徴になります。
ConvMFにおけるパラメータ推定法
ConvMFでは、パラメータ($U, V, W$)を最適化する為に、MAP推定(maximum a posteriori estimation)を行います。
事後分布の式を対数化してマイナスを掛け、いい感じに変形($\sigma^2$で割る!)と、以下のようになりますね(前パート参照)。
L(U,V,W|R, X, \lambda_U, \lambda_V, \lambda_W)
= \frac{1}{2} \sum_{i}^N \sum_{j}^M I_{ij}(r_{ij} - u_{i}^T v_j)^2 \\
+ \frac{\lambda_U}{2} \sum_{i}^N||u_i||^2 \\
+ \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \\
+ \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2
\\
(
\lambda_U = \frac{\sigma^2}{\sigma_U^2},
\lambda_V = \frac{\sigma^2}{\sigma_V^2},
\lambda_W = \frac{\sigma}{\sigma_W^2}
)
この式を最小化するような$U, V, W$を求めるわけです。
ConvMFの学習では、UとVとWの内2つを固定して、一つずつ最適化していく、Alternating Least Square(ALS)的なアプローチを取っていきます。
user latent matrix $U$とitem latent matrix $V$ の推定方法に関しては、ALS同様に、閉形式(closed-form, 要するに解析的に解ける式?)で解析的に計算することができます。
$$
u_i \leftarrow (V I_i V^T + \lambda_U I_K)^{-1}VR_i \tag{7}
$$
$$
v_j \leftarrow (U I_j U^T + \lambda_V I_K)^{-1}(UR_j + \lambda_V \cdot cnn(W, X_j)) \tag{8}
$$
$V$に関しては、$\lambda_V \cdot cnn(W, X_j)$が含まれているのが、通常のMFとの大きな違いであり、ConvMFの特徴ですね。
ここで
- ユーザiについて
- $I_i$ は$I_{ij} , (j=1, \cdots, M)$を対角要素とする対角行列。
- $R_i$ はユーザiについて$(r_{ij})_{j=1}^M$とするベクトル。
- つまり、ユーザiの各アイテムjに対する評価値が入ったベクトル!
- アイテムjについて
- $I_j$と$R_j$の定義は、$I_i$と$R_i$のものと同様。
- 式(8)はアイテム潜在ベクトル$v_j$を生成する際のCNNのDocument潜在ベクトル$s_j = cnn(W, X_j)$の効果を示している。
- $\lambda_V$はバランシングパラメータ(要は重み付け平均みたいな?, 意味合いとしては正則化項のハイパラ?)になる。
CNN内のパラメータWの推定方法に関しても、UとVを定数と仮定してWを推定する方針は同じです。以下の損失関数を最小化するようなパラメータ$W$を求めていきます。CNNに関しては次回のパートで実装をまとめていきます。
\varepsilon(W) = \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \\
+ \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2 + constant \tag{9}
最終的には、最適化された$U, V, W$により、「アイテム$j$に対するユーザ$i$の未知の評価 $r_{ij}$」を推定する事ができます。
r_{ij} \approx E[r_{ij}|u_i^T v_j, \sigma^2] \\
= u_i^T v_j = u_i^T \cdot (cnn(W, X_j) + \epsilon_j)
\tag{10}
ここまでで、簡単なConvMFの理論の復習は完了です。
Matrix Factorization部分の実装
さて、以下でMatrix Factorizationクラスを実装していきます。
Matrix Factorizationクラスに関しては、nishiba様の実装アプローチを参考にしまくりました。「なるほど、この情報をこのデータ型で格納しておくのか...!」と思う事が多々有りました...!
(コメントアウトが多すぎたり、docstringの書き方が汚い点はご了承いただきたく...笑)
Ratings格納用のクラスを定義する。
import os
from typing import Dict, Hashable, NamedTuple, List, Optional
import pandas as pd
import numpy as np
from tqdm import tqdm
class RatingData(NamedTuple):
"""ユーザiのアイテムjに対する評価値 r_{ij}を格納するクラス"""
user: int
item: int
rating: float
class IndexRatingSet(NamedTuple):
"""あるユーザi (or アイテムj)における、任意のアイテムj(or ユーザi)の評価値のリスト"""
indices: List[int] # user_id(もしくはitem_id)のList
ratings: List[float] # 対応するratingsのList
MatrixFactrizationクラスを定義する。
いざ、MatrixFactrizationクラスを定義していきます。まずはコンストラクタです。コンストラクタ.__init__()では、評価行列ratingsとMatrix Factrizationのハイパーパラメータn_factor, user_lambda, item_lambdaを引数として受け取ります。
n_item引数に関しては、評価値が一つも存在しないアイテムに対応可能にする為に設定しています。(評価値がないアイテムjに対しても、説明文書ベクトル$X_j$があれば、任意のユーザiに対して評価値の推定値$\hat{r}_{ij}$を推定できるはず...?)
# 略
class MatrixFactrization(object):
def __init__(self, ratings: List[RatingData], n_factor=300,
user_lambda=0.001, item_lambda=0.001, n_item: int = None):
"""コンストラクタ
Parameters
----------
ratings : List[RatingData]
ユーザiのアイテムjに対する評価値 r_{ij}を格納したList
n_factor : int, optional
latent factorの次元数, by default 300
user_lambda : float, optional
ConvMFのハイパーパラメータ \lambda_U, by default 0.001
item_lambda : float, optional
ConvMFのハイパーパラメータ \lambda_V, by default 0.001
n_item : int, optional
MFで使用するアイテム数, by default None
"""
data = pd.DataFrame(ratings)
# Rating matrixの形状(行数=user数、列数=item数)を指定。
self.n_user = max(data['user'].unique())+1 # 行数=0始まりのuser_id+1
self.n_item = n_item if n_item is not None else max(
data['item'].unique())+1 # 列数=0始まりのitem_id+1
self.n_factor = n_factor
self.user_lambda = user_lambda
self.item_lambda = item_lambda
# user latent matrix をInitialize
self.user_factor = np.random.normal(
size=(self.n_factor, self.n_user)
).astype(np.float32)
# item latent matrix をInitialize
self.item_factor = np.random.normal(
size=(self.n_factor, self.n_item)
).astype(np.float32)
# パラメータ更新時にアクセスしやすいように、Ratingsを整理しておく
self.user_item_list: Dict[int, IndexRatingSet]
self.item_user_list: Dict[int, IndexRatingSet]
# 各userに対する、Rating Matrixにおける非ゼロ要素のitemsとratings
self.user_item_list = {user_i: v for user_i, v in data.groupby('user').apply(
lambda x: IndexRatingSet(indices=x['item'].values, ratings=x['rating'].values)).items()}
# 各itemに対する、Rating Matrixにおける非ゼロ要素のusersとratings
self.item_user_list = {item_i: v for item_i, v in data.groupby('item').apply(
lambda x: IndexRatingSet(indices=x['user'].values, ratings=x['rating'].values)).items()}
コンストラクタの中盤では、user latent matrix $U$ (self.user_factor)とitem latent matrix $V$ (self.item_factor)の初期値を設定しています。
コンストラクタの終盤では、「各userに対する、Rating Matrixにおける非ゼロ要素のitemsとratings」と「各itemに対する、Rating Matrixにおける非ゼロ要素のusersとratings」をDict[int, IndexRatingSet]で整理しています。
これはMatrix Factrizationの学習プロセスにおいて、$U$と$V$のパラメータ更新式(上式の(7)(8))の$V I_i V^T$や$U I_j U^T$にアクセスしやすくする為です。
Matrix Factrization の学習プロセスを実装する。
MatrixFactrizationクラスの.fit()メソッドに、学習プロセスを実装しています。
.fit()メソッドでは、前述したようにALS(Alternating Least Square)と同様のプロセスで user latent matrix と item latent matrix を交互に最適化していきます。
user latent matrixの更新プロセスは.update_user_factors()メソッドに、item latent matrixの更新プロセスは.update_item_factors()メソッドに実装しており、innor関数的に.fit()メソッド内で呼び出しています。
なお、.update_item_factors()メソッドではadditional引数をオプションで受け取り可能にしており、ConvMFにおいては、この引数に「各アイテムに対応するdocument latent vecotor $s_j=CNN(W, X_j)$」を渡して$V_j$の推定に説明文書の情報を活用する事になります。
以下、実装内容になります。
# 略
class MatrixFactrization(object):
# 略
def fit(self, n_trial=5, additional: Optional[List[np.ndarray]] = None):
""" U:user latent matrix とV:item latent matrixを推定するメソッド。
Args:
n_trial (int, optional):
エポック数。何回ALSするか. Defaults to 5.
additional (Optional[List[np.ndarray]], optional):
文書潜在ベクトル document latent vector =s_j = Conv(W, X_j)のリスト. V_jの推定に使われる。
Defaults to None.
"""
# ALSをn_trial周していく!
# (今回はPMFだから実際には、AMAP? = Alternating Maximum a Posteriori)
for _ in tqdm(range(n_trial)):
# 交互にパラメータ更新
self.update_user_factors()
self.update_item_factors(additional)
def update_user_factors(self):
""" user latent vector (user latent matrixの列ベクトル)を更新する処理
"""
# 各user_id毎(=>各user latent vector毎)に繰り返し処理
for i in self.user_item_list.keys():
# rating matrix内のuser_id行のitem indicesとratingsを取得
indices = self.user_item_list[i].indices
ratings = self.user_item_list[i].ratings
# item latent vector(ここでは定数)を取得
v = self.item_factor[:, indices]
# 以下、更新式の計算(aが左側の項, bが右側の項)
a = np.dot(v, v.T)
# aの対角成分にlambda_uを追加?
a[np.diag_indices_from(a)] += self.user_lambda
b = np.dot(v, ratings) # V R_i
# u_{i}の値を更新 a^{-1} * b
self.user_factor[:, i] = np.linalg.solve(a, b)
# 逆行列と何かの積を取る場合,
# numpy.linalg.inv()じゃなくてnumpy.linalg.solve()の方が速いらしい...!
def update_item_factors(self, additional: Optional[List[np.ndarray]] = None):
"""item latent vector (item latent matrixの列ベクトル)を更新する処理
Parameters
----------
additional : Optional[List[np.ndarray]], optional
CNN(X_j, W)で出力された各アイテムの説明文書に対応するdocument latent vector
指定されない場合は、通常のPMF.
, by default None
"""
# 各item_id毎(=>各item latent vector毎)に繰り返し処理
for j in self.item_user_list.keys():
# rating matrix内のitem_id列のuser indicesとratingsを取得
indices = self.item_user_list[j].indices
ratings = self.item_user_list[j].ratings
# user latent vector(ここでは定数)を取得
u = self.user_factor[:, indices]
# 以下、更新式の計算(aが左側の項, bが右側の項)
a = np.dot(u, u.T)
# aの対角成分にlambda_Vを追加?
a[np.diag_indices_from(a)] += self.item_lambda
b = np.dot(u, ratings)
# ConvMFの場合は、\lambda_V・cnn(W, X_j)の項を追加
if additional is not None:
b += self.item_lambda * additional[j]
# v_{j}の値を更新 a^{-1} * b
self.item_factor[:, j] = np.linalg.solve(a, b)
最後に 評価値推定用のメソッドを定義
最後に、評価値の推定量$\hat{r}_{ij}$を求めるメソッドとして.predict()を定義しておきます。
# 略
class MatrixFactrization(object):
# 略
def predict(self, users: List[int], items: List[int]) -> np.ndarray:
"""user factor vectorとitem factor vectorの内積をとって、r\hat_{ij}を推定するメソッド。
Args:評価値を推定したい「userとitemのセット」を渡す。
users (List[int]): 評価値を予測したいユーザidのlist
items (List[int]): 評価値を予測したいアイテムidのlist
return:
入力したuser&itemに対応する、評価値の推定値\hat{r}_{ij}のndarray
"""
ratings_hat = []
for user_i, item_i in zip(users, items):
# ベクトルの内積を計算
r_hat = np.inner(
self.user_factor[:, user_i],
self.item_factor[:, item_i]
)
ratings_hat.append(r_hat)
# ndarrayで返す。
return np.array(ratings_hat)
テスト
実装したMatrixFactorizationクラスの挙動をテストしてみます。とりあえず今回は評価行列を受け取って学習まで!
make_rating_data()関数で、MatrixFactorizationクラスに入力する、評価行列ratingsを作成しています。
from typing import List, Tuple
import os
import pandas as pd
import numpy as np
from model.matrix_factorization import RatingData, MatrixFactrization
from config import Config
def make_rating_data() -> List[RatingData]:
"""評価値のcsvファイルから、ConvMFに入力するRatings情報(Rating Matrix)を作成する関数。
Returns:
List[RatingData]: Rating MatrixをCOO形式で。
"""
ratings = pd.read_csv(Config.ratings_path).rename(
columns={'movie': 'item'})
ratings['user'] = ratings['user'].astype(np.int32)
ratings['item'] = ratings['item'].astype(np.int32)
ratings['rating'] = ratings['rating'].astype(np.float32)
print('='*10)
n_item = len(ratings['item'].unique())
n_user = len(ratings['user'].unique())
print(f'num of unique items is ...{n_item:,}')
print(f'num of unique users is ...{n_user:,}')
print(f'num of observed rating is ...{len(ratings):,}')
print(f'num of values of rating matrix is ...{n_user*n_item:,}')
print(f'So, density is {len(ratings)/(n_user*n_item) * 100 : .2f} %')
# DataFrameからRatingDataに型変換してReturn。
return [RatingData(*t) for t in ratings.itertuples(index=False)]
if __name__ == '__main__':
ratings = make_rating_data()
mf = MatrixFactrization(ratings=ratings, n_factor=10)
mf.fit(n_trial=5, additional=None)
とりあえずMatrix Factorizationの学習プロセスまで問題なく回りました:)
まだオフライン評価指標等は計算していませんが、以降のパートでValidationも実装していきます。
また今回の実装では、学習プロセスにおける処理速度に問題を感じました。というのも、Matrix Factrizaitonにおけるハイパーパラメータの一つ「潜在次元数」n_facotorの値が10~20の場合は比較的スムーズに処理できますが、潜在次元数を100以上に増やしていくと時間計算量が一気に大きくなる印象を受けました。
今回の実装ではシンプルにforループでuser latent vectorとitem latent vectorを一つずつ推定しているので、何らかの方法(ex. 処理を並列化, Cython?, etc.)で高速化を図る必要があるのかなと感じました。
終わりに
今回の記事では「Convolutional Matrix Factorization for Document Context-Aware Recommendation」の理解と実装のパート2として、ConvMFのMatrix Factorization部分の実装をまとめました。
今回の実装を経て、Matrix Factorizationの学習処理に対して、何らかの方法(ex. 処理を並列化, Cython?, etc.)で高速化を図る必要があるのかなと感じました。
次回は、ConvMFの特徴である、CNNのパートを実装し、記事にまとめていきます。
そしてこの一連のConvMFの実装経験を通じて、"Ratingデータ"+"アイテムの説明文書"を活用した推薦システムについて実現イメージを得ると共に、"非常に疎な評価行列問題"や"コールドスタート問題"に対応し得る"頑健"な推薦システムについて理解を深めていきたいです。
理論や実装において、間違っている点や気になる点があれば、ぜひコメントにてアドバイスいただけますと嬉しいです:)