参考
- 元論文
- nishiba様のConvMF実装例(Chainerをお使いになってました!)
はじめに
KaggleのPersonalized Recommendationコンペに参加して以降、推薦システムが自分の中で熱くなっています。以前、Implicit Feedbackに対するモデルベースの協調フィルタリング(Matrix Factorization)の論文を読んで実装してみて、今度は更に実用的(?)で発展的な手法を触ってみたいと思い、「Convolutional Matrix Factorization for Document Context-Aware Recommendation」を読みました。この論文では、Matrix Factorizationによるモデルベース協調フィルタリングに、CNNを用いてアイテムの説明文書の情報を組み合わせる ConvMF(Convolutional Matrix Factorization)を提案しています。
今実装中ですが、なかなかPytorchと仲良くなれず、苦戦しております...。(ちなみに元論文はKerasで実装しておりました!)
パート1とした本記事では、ConvMFの理論と実装に向けた評価行列データ(MovieLens)と対応するアイテム説明文書データ(TMDb)の前処理についてまとめています。
理論
ConvMF(畳み込み行列分解)とは?
Convolutional Matrix Factorization(通称ConvMF)は、モデルベース協調フィルタリングにおいて評価行列のスパース性の上昇問題やコールドスタート問題に対応する為に提案された、Explicit FeedbackやImplicit Feedbackの評価情報に加えてアイテムの説明文書(ex. ニュース記事の中身、動画のタイトル、etc.)の情報を考慮した推薦手法の一つです。
その為に、ConvMFではモデルベース協調フィルタリングであるPMF(Probabilistic Matrix Factorization)にCNN(convolutional neural network)を統合しています。
その結果、ConvMFは最終的に協調情報と文脈情報の両方を効果的に利用することができ、評価データが極めて疎な場合でも、ConvMFは未知の評価を正確に予測することができる、らしいです...。
ConvMFの確率モデル
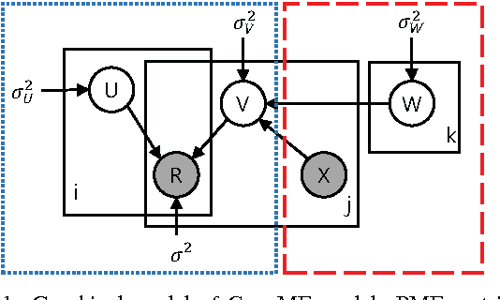
以下の図は、NLPに対するCNNモデルをPMF(確率的行列分解)モデルに統合した、ConvMFの確率モデルの概要を示したモノになります。
ちなみに上図において、各記号の意味合いは以下です。(順次まとめていきます)
- $U$: user latent model
- $V$: item latent model
- $R$: Rating Matrix
- $X$: アイテムのDescription(説明文)
- $W$: CNNのパラメータ達。
- $i, j$: それぞれ、各ユーザと各アイテムを表す添字。
- $k$:CNN内の各パラメータを表す添字(kに関しては、潜在ファクターの次元数の記号と混在してるかもしれません...?)
また問題設定として、N人のユーザとM個のアイテムがあり、観測された評価行列は$R\in \mathbb{R}^{N\times M}$行列で表現されるとします。
そして、その積($U^T \cdot V$)が評価行列 $R$を再構成するような、ユーザとアイテムの潜在モデル($U\in \mathbb{R}^{k\times N}$ と $V \in \mathbb{R}^{k\times M}$)を見つけることが目的になります。
確率的な観点からは、観測評価に関する条件付き分布(=すなわち尤度関数!!)は次式で与えられます。
$$
p(R|U, V, \sigma^2)
= \prod_{i}^{N} \prod_{j}^{M}
N(r_{ij}|u_i^T v_j, \sigma^2)^{I_{ij}}
\tag{1}
$$
ここで、
- $N (x|\mu, \sigma2)$は、一次元正規分布(ハイパラは$\mu, \sigma^2$)に従うxの確率密度関数。
- PMFでは「各$r_{ij}$間は独立」と仮定しているって事ですかね...!
- $I_{ij}$は「Ratingが観測されていれば1, 未観測であれば0を返す」ような指標関数。
- 要するに、$I_{ij}$を使って、観測済みのRatingのみを尤度関数に含める事を表現しているっぽいですね...!
また、user latent model$U$(各列ベクトルがユーザ因子ベクトル$u_i$)のPriori(事前分布)として、Spherical Gaussian prior(=>共分散行列が対角成分のみ。且つ全ての対角成分の値が等しい??)を選びます。
(要するに、$U_i$間は独立、各$U_i$はk次元正規分布に従って生成されると仮定...!)
u_i = \epsilon_i \\
\epsilon_i \sim N(\mathbf{0}, \sigma^2_U I)\\
p(U|\sigma^2_U) = \prod_{i}^{N} N(u_i|\mathbf{0}, \sigma_U^2 I)
\tag{2}
続いてitem latent modelですが、従来のPMF(確率的行列分解)におけるアイテム特徴行列の確率モデルとは異なり、ConvMFのアイテム因子行列は以下の3変数から生成されます:
- CNNにおけるパラメータ達$W$
- アイテムjのDescriptionを表す$X_j$
- 正規分布に従うと仮定された、撹乱項$\epsilon$
数式で書くと...$v_j$の生成仮定は...
v_j = cnn(W, X_j) + \epsilon_j \\
\epsilon_j \sim N(\mathbf{0}, \sigma^2_V I)
また、CNNのパラメータ$W$の各重み$w_k$に対しても、事前分布として、最も一般的に用いられるゼロ平均のSpherical Gaussian prior(=>つまり平均ベクトル0, 共分散行列が対角成分のみ、且つ全ての非ゼロ要素の値が等しい?)を設定します。
$$
p(W|\sigma^2_W) = \prod_k N(w_k|0, \sigma_W^2) \tag{3}
$$
したがって、アイテム特徴行列に対する条件付き分布は次式で与えられます。
$$
p(V|W, X, \sigma^2_V) = \prod_j^{M}
N(v_j|cnn(W,X_j),\sigma_V^2I) \tag{4}
$$
ここで、
- $X$: アイテムに関する記述文書の集合
- $X_j$はアイテムjの特徴量
- $cnn(W,X_j)$:
- CNNモデルから得られるDocument latent vactor($cnn(W,X_j)$)。
- $v_i$の事前分布の平均$\mu$として用いられている。
- このDocument Latent VectorがCNNとPMFの橋渡しになる。
- これが説明文書(すなわち、アイテムが持つ特徴量、コンテキスト)と評価(Explicit or Implicit feedback)の両方を考慮するために重要な役割を果たすらしい...!
$cnn(W,X_j)$について
ここに関しては追記するかもしれないし、しないかもしれません。
NLPへのCNNパートの実装の際に記述するかもしれません!
ここでは、アイテムjに関する説明文$X_j$を入力として、document latent vector $s_j = cnn(W,X_j) \in \mathbf{R}^{factorの数}$を出力する関数、とだけ記述しておきます。
ConvMFにおけるパラメータ推定法
ConvMFでは、パラメータ($U, V, W$)を最適化する為に、MAP推定(maximum a posteriori estimation)を行います。
\max_{U, V, W} p(U, V, W|R, X, \sigma^2, \sigma_U^2, \sigma_V^2, \sigma_W^2) \\
= \max_{U, V, W}[尤度関数 \times 事前分布] \\
= \max_{U, V, W}[
p(R|U, V, \sigma^2)
\cdot p(U|\sigma_U^2)
\cdot p(V|W, X, \sigma_V^2)
\cdot p(W|\sigma_W^2)
] \tag{5}
式(5)の3行目に、上述した式(1)~(4)を代入する事で、目的関数の値を計算できますね。
更にここから式(5)を対数化してマイナスを掛け、いい感じに変形($\sigma^2$で割る!)と、以下のようになります。
L(U,V,W|R, X, \lambda_U, \lambda_V, \lambda_W)
= \frac{1}{2} \sum_{i}^N \sum_{j}^M I_{ij}(r_{ij} - u_{i}^T v_j)^2 \\
+ \frac{\lambda_U}{2} \sum_{i}^N||u_i||^2 \\
+ \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \\
+ \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2
\tag{6}
\\
(
\lambda_U = \frac{\sigma^2}{\sigma_U^2},
\lambda_V = \frac{\sigma^2}{\sigma_V^2},
\lambda_W = \frac{\sigma}{\sigma_W^2}
)
この式(6)を最小化するような$U, V, W$を求める事を目指します。
ではどのように最適化していくのでしょうか?
どうやら、UとVとWの内2つを固定して、一つずつ最適化していく、Alternating Least Square(ALS)的なアプローチを取っていくようです!
UとVの推定方法
UとVの推定方法に関しては、ALSと同じような印象です!
(今回は推定法がLeast SquareではなくMAPなので、AMAPとでもいうのでしょうか?)
user latent model $U$に関して、具体的には、W と Vを一時的に一定とみなすと、式(6)は Uに関して二次関数となります。そして、Uの最適解は、最適化関数$L$を$u_i$に関して以下のように微分するだけで、閉形式(closed-form, 要するに解析的に解ける式?)で解析的に計算することができます。
$$
u_i \leftarrow (VI_i V^T + \lambda_U I_K)^{-1}VR_i \tag{7}
$$
item latent model $V$も同様に、以下のような更新式を導出する事ができます。
($V$に関しては、$\lambda_V \cdot cnn(W, X_j)$が含まれているのが、通常のMFとの大きな違い!)
$$
v_j \leftarrow (U I_j U^T + \lambda_V I_K)^{-1}(UR_j + \lambda_V \cdot cnn(W, X_j)) \tag{8}
$$
ここで
- ユーザiについて
- $I_i$ は$I_{ij} , (j=1, \cdots, M)$を対角要素とする対角行列。
- $R_i$ はユーザiについて$(r_{ij})_{j=1}^M$とするベクトル。
- つまり、ユーザiの各アイテムjに対する評価値が入ったベクトル!
- アイテムjについて
- $I_j$と$R_j$の定義は、$I_i$と$R_i$のものと同様。
- 式(8)はアイテム潜在ベクトル$v_j$を生成する際のCNNのDocument潜在ベクトル$s_j = cnn(W, X_j)$の効果を示している。
- $\lambda_V$はバランシングパラメータ(要は重み付け平均みたいな?, 意味合いとしては正則化項のハイパラ?)になる。
Wの推定方法
CNN内のパラメータWの推定方法に関しても、UとVを定数と仮定してWを推定する方針は同じです。
しかし、Wはmax pooling層や非線形活性化関数などCNNアーキテクチャの特徴と密接に関係している為、UやVのように解析的に解く事はできません。
それでも、上述したようにUとVが一時的に定数と仮定する事で、$L$は以下のように「$W$に関してL2正則化項を持つ二乗誤差関数」として解釈する事ができます。
\varepsilon(W) = \frac{\lambda_V}{2} \sum_{j}^M ||v_j - cnn(W,X_j)||^2 \\
+ \frac{\lambda_W}{2} \sum_{k}^{|W_k|}||w_k||^2 + constant
\tag{9}
よって上式を最小化すべき損失関数(目的関数)として勾配降下法やら逆誤差伝搬やらを用いて、問題なく$W$も最適化する事ができそうです。
Uの最適化→Vの最適化→Wの最適化→...を繰り返す...!
パラメータ全体の最適化処理($U, V, W$は交互に更新される)は収束されるまで(エポック数分)繰り返されます。
最終的には、最適化された$U, V, W$により、「アイテム$j$に対するユーザ$i$の未知の評価 $r_{ij}$」を推定する事ができます。
r_{ij} \approx E[r_{ij}|u_i^T v_j, \sigma^2] \\
= u_i^T v_j = u_i^T \cdot (cnn(W, X_j) + \epsilon_j)
ここまでで、ConvMFの理論はざっくり完了ですね。
やっぱり数式は世界共通なので、英語論文読んでいる最中に出てきてくれると救われた気分になります...!砂漠地帯の中のオアシス的な存在ですね:)
実験用の評価データの準備
元データの用意
前の章まででConvMFの理論まとめは終了で、ここからは実装への準備として、実験用の評価データを準備していきます。
本記事では評価値のデータとして、Explicit Feedbackである「MovieLens」を使用します。
今回はMovieLens10m (ML-10m) をダウンロードしました。
ちなみに元論文のExperimentでは、比較的 密なRatingとして「MovieLens-1m (ML-1m)」「MovieLens10m (ML-10m) 」、疎なRatingとして「Amazon Instant Video (AIV)」を使用しているようです。
またMovieLensには、アイテムの説明文書($X_j$)が含まれていない為、「TMDb(The Movie Database)」というデータセットから、対応するアイテムの文書を取得します。(元論文でも同じようにしているようです)
以下のkaggle のLinkからダウンロードさせていただきました。
評価データの整形
このパートでは、用意した元データを整形して、ConvMFの学習の為の入力値として扱いやすい形にしていきます。
以下で記述されたコードに関しては、nishiba様のgithubを参考にさせていただきました。
(参考というか、適宜コメントアウトを差し込みながらの写経です!「なるほど...こういう書き方をすると可読性が高くなったりメンテナンスしやすいのかな...」と大変勉強になりました:))
import os
class Config:
data_dir = r'data'
# 元データ
movie_len_dir = os.path.join(data_dir, 'ml-10M100K')
# movie_len_dir = os.path.join(data_dir, 'ml-1m')
tmdb_movies_path = os.path.join(data_dir, 'tmdb_5000_movies.csv')
tmdb_credits_path = os.path.join(data_dir, 'tmdb_5000_credits.csv')
# 整形後のRating matrixとDescripiton documents
ratings_path = os.path.join(data_dir, 'ratings.csv')
descriptions_path = os.path.join(data_dir, 'descriptions.csv')
import os
import re
import pandas as pd
import numpy as np
from config import Config
def make_descriptions()->pd.DataFrame:
"""アイテムのDescription documentのファイルを整形する関数.
Returns:
pd.DataFrame: 整形されたDescription document
"""
# Movielensデータを読み込み
title_id = pd.read_csv(
os.path.join(Config.movie_len_dir, 'movies.dat'),
sep='::',
engine='python',
names=['id', 'title', 'tag']
)
title_id = title_id[['id', 'title']]
# titleカラムの前処理:title(year)=>titleのみに変換
title_id['title'] = title_id['title'].apply(
lambda x: re.sub(r'\(\d+\)', '', x).rstrip())
print(title_id.head())
# アイテムの説明文書のデータを読み込み
movie_df = pd.read_csv(Config.tmdb_movies_path)[['title', 'overview']]
print(movie_df.head())
# title_idとmovie_dfにおいて、titleカラムの表記をそろえる(全て小文字に)
movie_df['title'] = movie_df['title'].apply(lambda x: x.lower())
title_id['title'] = title_id['title'].apply(lambda x: x.lower())
# merge
merged = pd.merge(movie_df, title_id, on='title', how='inner')
merged = merged.rename(columns={'overview': 'description'})
merged['id'] = merged['id'].astype(np.int32)
print(merged.head())
return merged
def make_ratings()->pd.DataFrame:
"""MovieLensのデータから、評価行列を整形する関数
Returns:
pd.DataFrame: _description_
"""
ratings = pd.read_csv(
os.path.join(Config.movie_len_dir, 'ratings.dat'),
sep='::',
engine='python',
names=['user', 'movie', 'rating', 'timestamp']
)
ratings = ratings[['user', 'movie', 'rating']]
# 型変換
ratings['user'] = ratings['user'].astype(np.int32)
ratings['movie'] = ratings['movie'].astype(np.int32)
ratings['rating'] = ratings['rating'].astype(np.float32)
print(ratings.head())
return ratings
def preprocess():
descriptions = make_descriptions()
ratings = make_ratings()
# re-indexing
users = ratings['user'].unique()
user_map = dict(zip(users, range(len(users)))) # ユーザ対応表の作成
movies = descriptions.id.unique()
movie_map = dict(zip(movies, range(len(movies)))) # アイテム対応表の作成
# user id=>user通し番号、item id=>item通し番号に変換.
ratings.user = ratings.user.apply(lambda x: user_map.get(x, None))
ratings.movie = ratings.movie.apply(lambda x: movie_map.get(x, None))
descriptions.id = descriptions.id.apply(lambda x: movie_map.get(x, None))
# 欠損値があるレコードを除去
ratings = ratings.dropna()
descriptions = descriptions.dropna()
# export
ratings.to_csv(os.path.join(Config.data_dir, 'ratings.csv'), index=False)
descriptions.to_csv(os.path.join(Config.data_dir, 'descriptions.csv'), index=False)
if __name__ == '__main__':
preprocess()
適宜、print()でコンソール出力して、DataFrameの中身を確認しています。
出力は以下のような感じになります。
id title
0 1 Toy Story
1 2 Jumanji
2 3 Grumpier Old Men
3 4 Waiting to Exhale
4 5 Father of the Bride Part II
title overview
0 Avatar In the 22nd century, a paraplegic Marine is di...
1 Pirates of the Caribbean: At World's End Captain Barbossa, long believed to be dead, ha...
2 Spectre A cryptic message from Bond’s past sends him o...
3 The Dark Knight Rises Following the death of District Attorney Harve...
4 John Carter John Carter is a war-weary, former military ca...
user movie rating
0 1 122 5.0
1 1 185 5.0
2 1 231 5.0
3 1 292 5.0
4 1 316 5.0
また、最終的に生成されたratings.csvとdescriptions.csvの内容な以下のようになります。
user movie rating
0 1 122 5.0
1 1 185 5.0
2 1 231 5.0
3 1 292 5.0
4 1 316 5.0
title description id
0 pirates of the caribbean: at world's end Captain Barbossa, long believed to be dead, ha... 53125
1 spider-man 3 The seemingly invincible Spider-Man goes up ag... 52722
2 superman returns Superman returns to discover his 5-year absenc... 46530
3 quantum of solace Quantum of Solace continues the adventures of ... 63113
4 pirates of the caribbean: dead man's chest Captain Jack Sparrow works his way out of a bl... 45722
Ratingsの保存形式が「行=各ユーザ、列=各アイテム」のRating Matrixになっているのではなく、「行=Rating Matrixの非ゼロ要素、列=['user_id', 'item_id', 'rating]」になっているのが一応注意点です。
各レコードが[行index, 列index, 要素]になっているので、これはいわゆる、疎行列のデータ格納形式の一つのCOO形式(Coordinate, 座標形式)ですね...!
多くの場合Rating Matrixは非ゼロ要素を大量に含むので、こういった疎行列特有の格納形式を活用して、メモリ消費を節約しているようです。
とりあえず、これでConvMFを学習させる為に必要なデータが整形できました!(たぶん!)
終わりに
今回は「Convolutional Matrix Factorization for Document Context-Aware Recommendation」の理解と実装の第一ステップとして、ConvMFの理論と、実装に使用するサンプルデータの作成までまとめました。
今後は、Matrix Factorizationのパート、CNNのパートを順次実装し、記事にまとめていきます。
そしてこの一連のConvMFの実装経験を通じて、"Ratingデータ"+"アイテムの説明文書"を活用した推薦システムについて実現イメージを得ると共に、"非常に疎な評価行列問題"や"コールドスタート問題"に対応し得る"頑健"な推薦システムについて理解を深めていきたいです。
間違っている点や気になる点があれば、ぜひコメントにてアドバイスいただけますと嬉しいです:)