SPH法の理論と実装 ~理論編1~ と SPH法の理論と実装 ~理論編2~ で紹介したSPH法で実際に計算できるようにします。前回記事から半年近く開いてしまいました。すみません。
時間積分
理論編ではSPH法による空間離散化の方法を書きました。これを各ステップごとに時間積分していけばとりあえず計算できます。
時間積分スキームはEuler法やRunge-Kutta法など色々ありますが、2次精度くらいの手法がよく使われます。SPH法の計算式
$$
F_i = \sum_j \frac{m_j}{\rho_j} F_j W_{ij}
$$
は精度がそれほど高くないため (高々2次精度。粒子分布の乱雑さに寄っては0次精度)、高次の積分スキームを使ってもあまり効果がありません。
ここではLeap-frog法を紹介します。
Leap-frog法
Leap-frog法は2次精度のシンプレクティックスキームで、エネルギーや角運動量の保存性に優れるため、重力計算や分子動力学でよく使われます。
位置、速度、加速度をそれぞれ $\boldsymbol{r}, \boldsymbol{v}, \boldsymbol{a}$ で表すとします。また、上付き添字はステップ数を示すとします。このとき、$k$ステップ目から$(k+1)$ステップ目への時間積分を
\boldsymbol{v}^{k+1/2} = \boldsymbol{v}^k + \boldsymbol{a}^k \frac{\Delta t}{2}\\
\boldsymbol{r}^{k+1} = \boldsymbol{r}^k + \boldsymbol{v}^{k+1/2} \Delta t\\
\boldsymbol{v}^{k+1} = \boldsymbol{v}^{k+1/2} + \boldsymbol{a}^{k+1} \frac{\Delta t}{2}
で計算します。
重力やLennard-Jonesポテンシャルは加速度が速度に依存しないため、$\boldsymbol{r}^{k+1}$ から $\boldsymbol{a}^{k+1}$ が計算できますが、SPH法は速度に依存するため工夫が必要です。例えば、
$$
\boldsymbol{v}^{k+1'} = \boldsymbol{v}^k + \boldsymbol{a}^k \Delta t
$$
で速度を1次精度で外挿して加速度を計算します。Price et al. (2018)では$\boldsymbol{v}^{k+1'}$ と $\boldsymbol{v}^{k+1}$の差が大きいと加速度を再計算するようにしています。
内部エネルギーは速度と同様に積分します。
時間刻み
数値計算では、$\Delta t$の間に情報が伝播する領域は、実現象における伝播領域より大きくする必要があります。もし逆の場合、伝播すべき領域まで情報が届いていないことになり、解が物理的な信頼性を持たなくなります。この時間刻みの制限をCFL条件と呼びます。
SPH法では、Monaghan (1997)の人工粘性と合わせて
\Delta t = \min_i [\Delta t_i]\\
\Delta t_i = C_{\rm cfl} \frac{h_i}{\max_j [v_{ij}^{\rm sig}]}\\
v_{ij}^{\rm sig} = c_i + c_j - 3 w_{ij},
w_{ij} = (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot \frac{\boldsymbol{r}_i - \boldsymbol{r}_j}{|\boldsymbol{r}_i - \boldsymbol{r}_j|}
のようにして時間刻みを計算することが多いです。ここで、$C_{\rm cfl}$は1以下の定数で、0.3程度の値がよく使われます。
強い力を受けた粒子が1ステップで動きすぎないようにするための条件
$$
\Delta t_i = C_{\rm force} \sqrt{\frac{h_i}{|\boldsymbol{a}_i|}}
$$
もよく使われます。
サンプルコードの実装
サンプルコードでは以下のようにして時間を進めています。
- 時間刻み $\Delta t$ の計算
- 時間積分 (1段階目)
$$
\boldsymbol{v}^{k+1/2} = \boldsymbol{v}^k + \boldsymbol{a}^k \frac{\Delta t}{2}
$$
$$
\boldsymbol{r}^{k+1} = \boldsymbol{r}^k + \boldsymbol{v}^{k+1/2} \Delta t
$$
$$
\boldsymbol{v}^{k+1'} = \boldsymbol{v}^k + \boldsymbol{a}^k \Delta t\
$$
$$
u^{k+1/2} = u^k + \dot{u}^k \frac{\Delta t}{2}\
$$
$$
u^{k+1'} = u^k + \dot{u}^k \Delta t\
$$ - 密度、圧力などの計算
- 加速度、内部エネルギーの時間微分の計算
- 時間積分 (2段階目)
$$
\boldsymbol{v}^{k+1} = \boldsymbol{v}^{k+1/2} + \boldsymbol{a}^{k+1} \frac{\Delta t}{2}
$$
$$
u^{k+1} = u^{k+1/2} + \dot{u}^{k+1} \frac{\Delta t}{2}
$$
独立時間刻み
サンプルコードでは全粒子の時間刻みを揃えていますが、それぞれの粒子にそれぞれの時間刻み幅を与える場合もあります。大規模シミュレーション用のコードは大体そうなっていると思います。
CFL条件による時間刻み条件が厳しい粒子だけ細かい時間刻みで計算し、他の粒子は時間刻みを大きくすることで、計算量を減らすことができます。
その一方で、時間刻みが異なる粒子間に働く相互作用が、作用反作用の法則を完全には満たさなくなるというデメリットもあります。
近傍粒子探索
粒子間相互作用を単純に実装すると
for(int i = 0; i < N; ++i) {
for(int j = 0; j < N; ++j) {
auto r_ij = distance(i, j); // i-j間の距離
if(r_ij < h_i) {
calc_force(i, j); // j -> i の力
}
}
}
のようなコードになると思います。しかし、これでは粒子数$N$に対して計算量が$\mathcal{O}(N^2)$となってしまうため、粒子数を増やして計算していくのが非常に厳しくなります。そのため、何かしらの工夫をしてやる必要があります。
ツリー法 (Barnes & Hut 1986; Hearnquist & Katz 1989)を使うことで計算量を$\mathcal{O}(N {\rm log} N)$に減らすことができます。
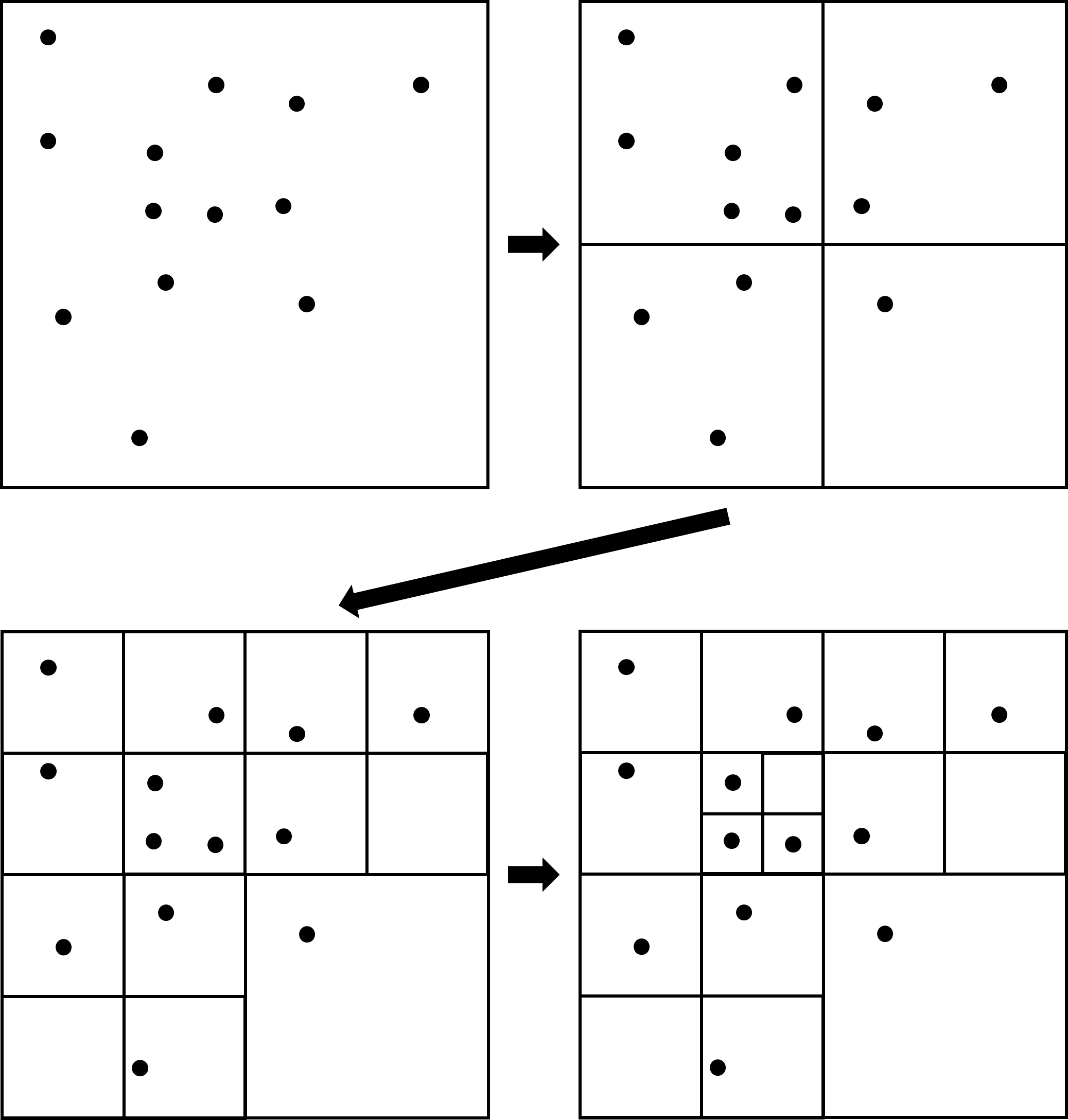
ツリー法の概念図です。木構造を使って粒子をこんな感じに分割していきます。2次元では4分木、3次元では8分木となります。
ノードに対して近傍判定を行うことで、遠くのノードにある粒子をまとめて近傍粒子候補から除外できるようになります。
ツリー構築の詳しい実装方法は
が参考になると思います。
自己重力
N体シミュレーションでは粒子を質点として扱うため、粒子間に働く重力は単純に逆二乗則で計算できます (実際は粒子同士が近づきすぎたときのためにソフトニングを入れるのですが)。
一方、SPH法では粒子が体積を持っているということを考慮に入れる必要があります。
位置$\boldsymbol{r}$における重力ポテンシャルを
$$
\Phi(\boldsymbol{r}) = -G \sum_j m_j \phi(|\boldsymbol{r} - \boldsymbol{r}_j|, h)
$$
と書けるとすると、Poisson方程式
$$
\nabla^2 \Phi = 4 \pi G \rho
$$
と、SPH法の密度の計算式を合わせて
$$
W(r,h) = - \frac{1}{4 \pi r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial \phi}{\partial r} \right)
$$
という方程式が得られます。これから$\phi$の関数形を求め、Euler-Lagrange方程式を使うと、粒子に働く重力を計算できるようになります (Price & Monaghan 2007)。
ある粒子に働く重力は、その粒子以外のすべての粒子からの寄与を考える必要があります。そのため、普通に計算すると$\mathcal{O}(N^2)$の計算量になってしまいます。
しかしながら、前述のツリー法を使って、遠くのノードにある粒子の寄与を一度にまとめて計算することで、$\mathcal{O}(N {\rm log} N)$まで減らすことができます。
最後に
理論編1~実装編までの知識で、とりあえず動くコードは作れると思います。めでたしめでたし。
なにか書き忘れていることがあったら追記するかもしれません。
参考文献
- Barnes, J., & Hut, P. (1986). A hierarchical O(N log N) force-calculation algorithm. Nature, 324(6096), 446–449. https://doi.org/10.1038/324446a0
- Hernquist, L., & Katz, N. (1989). TREESPH - A unification of SPH with the hierarchical tree method. The Astrophysical Journal Supplement Series, 70, 419. https://doi.org/10.1086/191344
- Monaghan, J. J. (1997). SPH and Riemann Solvers. Journal of Computational Physics, 136(2), 298–307. https://doi.org/10.1006/jcph.1997.5732
- Price, D. J. et al. (2018). Phantom : A Smoothed Particle Hydrodynamics and Magnetohydrodynamics Code for Astrophysics. Publications of the Astronomical Society of Australia, 35(2013), e031. https://doi.org/10.1017/pasa.2018.25
- Price, D. J., & Monaghan, J. J. (2007). An energy-conserving formalism for adaptive gravitational force softening in smoothed particle hydrodynamics and N-body codes. Monthly Notices of the Royal Astronomical Society, 374(4), 1347–1358. https://doi.org/10.1111/j.1365-2966.2006.11241.x