Barnes-Hut treeの構築 (モートンキー版)

はじめに

わけあって、重力多体系の計算で使われるBarnes-Hut treeを構築することになったので覚書の続きの続き。

コードは
https://github.com/kaityo256/barnes-hut
に置いてあるソースのうちbarnes-hut-morton.rbがそれ。

BHツリーとモートンキー

ちなみに、多くの現代的なBHツリーコードの実装では、まずモートンキーを作ってそれでソートしたら大体ツリーできました、的な方法をつかいます。キー生成は並列化できるので、あとは良い並列ソートを使えば大変良い性能がでるので。 https://t.co/jwxpo5vfKv

— Jun Makino (@jun_makino) 2017年4月26日

ということだそうなので、モートンキーを使ってBHツリーを作ってみることに。実用コードはビット演算とか使ってるっぽいんだけど、自分の理解のテストのためなので、この記事では速度とか気にしないことにする。木の構築もきっともっと賢い方法があると思うけど気にしない。

前回はノードクラスを作って、明示的に木を構築したが、この木の状態を線形4分木で表現することにして、さらにその線形4分木をハッシュで実装する。

以下、「モートンキー」について、「グローバルなモートンキー」と「ローカルなモートンキー」を使い分ける。ローカルなモートンキーとは、左上のインデックスが0になっているもの。たとえばレベル3の分割では、空間が8*8の64個にわかれているので、ローカルなインデックスは0から63まである。これらは、線形化した4分木では、レベル０が1個、レベル1が4個、レベル2が16個あるため、1+4+16=21番目から格納されることになる。この最初にインデックスを足した21から84までをレベル3のグローバルなモートンキーと呼ぶことにする。¹

アルゴリズム

モートン順序についてはこのページがわかりやすかったので、そちらを参照。特にこのページの図を見ながらの方が理解しやすいと思う。

基本的には最初に書いたinsertion版のアルゴリズムを、モートンキーとハッシュで実装するだけ。

ノードに関しては前の記事と同じだが、再掲しておく。

ノードとは、以下の条件を満たすものである。

• ノードは、部分空間を担当している。
• ノードは、「粒子がいない」「粒子が一個だけいる」「粒子が二個以上いる」の三通りの状態がある
• 粒子が二個以上いるノードは、担当する空間が4分割され、それぞれを子ノードが担当している

ノードの状態が三通りあるので、そこに粒子を追加しようとすると、三通りの処理が必要になる。

1. 粒子がいない場合： 単に粒子を追加すれば良い
2. 粒子が一個だけいる場合： 自分を四分割し、もともといた粒子と、追加された粒子をそれぞれ子ノードに追加する
3. 粒子が二個以上いる場合： 追加された粒子を子ノードに渡す

ノードの三種類の状態は、

• ノードに対応するkeyが定義されていなければ空
• ノードに対応するkeyの値が0以上なら、そのノードには粒子がひとつだけいて、その粒子番号がその値
• ノードに対応するkeyの値が-1なら粒子が二個以上いるので、担当する空間が4分割され、それぞれを子ノードが担当している

と表現しよう。

後は同じで、ルートノードに対応するkeyに粒子を追加しようとして、もしぶつかってたり子ノードがある場合には、子ノードに対応するkeyを取得して再帰、ということを繰り返せばよい。

実装

実装の概要(インタフェース)

モートンキーのハッシュを管理するクラス、BHTreeを作ってみる。²
コンストラクタでは、一辺のサイズを受け取り、ハッシュを初期化しておく。

class BHTree
  def initialize(size)
    @keyhash = Hash.new
    @size = size
  end
end

前回と同様、粒子情報はこうやって用意しておこう。

Particle = Struct.new(:x, :y)
srand(2)
L = 256.0
q = []
10.times do
  x = L*rand
  y = L*rand
  q.push Particle.new(x, y)
end

最終的に、粒子番号とグローバルなモートンキーの対応がほしいので、その配列も用意しておく。

mkey = Array.new(q.size)

この状態で、粒子をルートノード(に対応するkeyである0番)に追加してけば、最終的にmkeyにモートンキーが入っていて欲しい。

tree = BHTree.new(L)

q.size.times do |i|
  tree.add(0,i,mkey,q)
end

この中身を実装していけばよい。

粒子の追加処理

まず、addの中身。addの引数は

• key 追加しようとしているノードに対応するグローバルなモートンキー* i 追加しようとしている粒子番号
• mkey 粒子番号とモートンキーの対応を表す配列
• q 粒子座標

となっている。後は、ハッシュの値によって三通りの処理にわけるのは前の記事と同じ。中身はこんな感じになるだろう。

  def add(key, i, mkey, q)
    if !@keyhash.has_key?(key)
      @keyhash[key] = i
      mkey[i] = key
    elsif @keyhash[key] == -1
      add_sub(key, i, mkey, q)
    else
      j = @keyhash[key]
      @keyhash[key] = -1
      add_sub(key, j, mkey, q)
      add_sub(key, i, mkey, q)
    end
  end

子ノードへの粒子追加処理

次に、子ノードに粒子を追加する処理であるadd_subの実装をする。処理としてはこんな感じになるだろう。

1. まず、グローバルなモートンキーから、分割レベルlevelを得る。
2. 次に、自分の担当する領域の左上の座標x, yを得る
3. 粒子が4つの子ノードのどこにいくかを計算する ('id')
4. その子ノードのグローバルモートンキーを計算する
5. その子ノードに追加を依頼する

グローバルモートンキーからレベルを得る処理key2levelと、座標を得る処理key2posについては後述。

  def add_sub(key, i, mkey, q)
    level = key2level(key)
    x, y = key2pos(key)
    s = @size.to_f / (2 ** (level+1))
    ix = ((q[i].x - x)/s).to_i
    iy = ((q[i].y - y)/s).to_i
    id = ix + iy * 2
    key = key - (4**level - 1)/3
    key = key << 2
    key = key + id
    key = key + (4**(level+1) -1)/3
    add(key, i, mkey, q)
  end

前述の処理をそのまま書いただけなので、難しいことは無いと思うが、「子ノードのグローバルモートンキー」の計算だけちょっとややこしい。

まず、グローバルモートンキーからローカルなモートンキーを得る。レベルlevelのローカルなモートンキーは、線形4分木の(4**level-1)/3番目から始まるから、それを引けばローカルなモートンキーとなる。

key = key - (4**level - 1)/3

次に、モートンキーの性質から、ローカルなモートンキーを4倍し、自分の子ノードのid(0から3まで)を足すと、次のレベルのローカルなモートンキーになる。

    key = key << 2
    key = key + id

最後に、線形4分木において、次のレベルのローカルなモートンキーの0番目の位置を足せば、グローバルなモートンキーとなる。

    key = key + (4**(level+1) -1)/3

あとはそのキーについて再帰すれば、そのキーに対応する子ノードに粒子の追加を依頼したことになる。

    add(key, i, mkey, q)

グローバルモートンキーからレベルへの変換

線形4分木では、異なるレベルのローカルなモートンキーが順番に保存されている。レベル0が全空間とすると、レベル$L$のモートンキーは$4^L$個あるので、レベル$L$のローカルなモートンキーの0番目のグローバルなインデックス(線形4分木のインデックス)は、等比級数の和の公式から

\frac{4^L-1}{3}

で与えられる。さて、グローバルなモートンキー$x$が与えられたとき、そのレベルが知りたい。もしレベル$L$であったならば、

\frac{4^L-1}{3} \le x < \frac{4^{L+1}-1}{3}

が成り立つ。ここから$L$を求めたいので、式を変形して

4^L \le 3x+1 < 4^{L+1}

ここから、$\log_4 3x+1$を計算すればよいことがわかる。せっかくRubyのIntegerにbit_lengthというメソッドがあるのでそれを使うと、

  def key2level(key)
    ((3*key+1).bit_length+1)/2-1
  end

と実装できる。

グローバルモートンキーから左上の座標を取得

ローカルなモートンキーの性質から、下位から2bitずつとると、それがそのレベルにおける位置を表している。したがって、

1. レベルを得る
2. そのレベルにおけるサイズsを得る
3. ローカルなモートンキーの下位2bitから、相対的な位置を取得し、x座標、y座標に足す
4. サイズsを2倍し、上位のレベルについて3.を繰り返す

とすれば、左上の座標を得ることができる。実装例はこんな感じ。

  def key2pos(key)
    x = 0.0
    y = 0.0
    level = key2level(key)
    key = key - (4**level -  1)/3
    s = @size.to_f / (2**level).to_f
    level.times do
      x = x + (key & 1)*s
      key = key >> 1
      y = y + (key & 1)*s
      key = key >> 1
      s = s * 2.0
    end
    return x,y
  end

実装のまとめ

以上をまとめるとBHTreeクラスはこんな感じになる。

class BHTree
  def initialize(size)
    @keyhash = Hash.new
    @size = size
  end

  def key2level(key)
    ((3*key+1).bit_length+1)/2-1
  end

  def key2pos(key)
    x = 0.0
    y = 0.0
    level = key2level(key)
    key = key - (4**level -  1)/3
    s = @size.to_f / (2**level).to_f
    level.times do
      x = x + (key & 1)*s
      key = key >> 1
      y = y + (key & 1)*s
      key = key >> 1
      s = s * 2.0
    end
    return x,y
  end

  def add_sub(key, i, mkey, q)
    level = key2level(key)
    x, y = key2pos(key)
    s = @size.to_f / (2 ** (level+1))
    ix = ((q[i].x - x)/s).to_i
    iy = ((q[i].y - y)/s).to_i
    id = ix + iy * 2
    key = key - (4**level - 1)/3
    key = key << 2
    key = key + id
    key = key + (4**(level+1) -1)/3
    add(key, i, mkey, q)
  end

  def add(key, i, mkey, q)
    if !@keyhash.has_key?(key)
      @keyhash[key] = i
      mkey[i] = key
    elsif @keyhash[key] == -1
      add_sub(key, i, mkey, q)
    else
      j = @keyhash[key]
      @keyhash[key] = -1
      add_sub(key, j, mkey, q)
      add_sub(key, i, mkey, q)
    end
  end

end

おもったより短いですね。

描画

以上で、粒子の座標を食わせたら、グローバルなモートンキー(線形4分木のインデックス)が得られるコードができた。これを描画するには、グローバルなモートンキーを与えられたら、その領域まで分割した線を描くメソッドが必要。ちゃんと考えれば無駄の無いコードが書けるのだろうが、ここでは手抜きして、自分のレベルから一番上のレベルまで描画するコードを書いてしまう。これだと一番上の線がなんども書かれちゃうけど、まぁデバッグ用なので。

というわけでBHTreeクラスに描画メソッドを追加する。モートンキーと描画コンテキストをもらったら、対応する分割を描画する。

class BHTree

  def parentkey(key)
    return 0 if key == 0
    level = key2level(key)
    key = key - (4**level -  1)/3
    key = key >> 2
    key = key + (4**(level-1) -  1)/3
    key
  end

  def draw(key, context)
    context.set_source_rgb(0, 0, 0)
    key = parentkey(key)
    level = key2level(key)
    hs = @size / (2**(level+1))
    x, y = key2pos(key)
    context.move_to(x + hs, y)
    context.line_to(x + hs, y + hs*2)
    context.move_to(x , y + hs)
    context.line_to(x + hs*2, y + hs)
    context.stroke
    if key !=0
      draw(key, context)
    end
  end
end

親のキーが必要になるので、それも追加している。

pngに保存するルーチンも少しだけ修正する。

def save_png(filename, size, q, mkey, tree)
  surface = Cairo::ImageSurface.new(Cairo::FORMAT_RGB24, size, size)
  context = Cairo::Context.new(surface)
  context.set_source_rgb(1, 1, 1)
  context.rectangle(0, 0, size, size)
  context.fill
  context.set_source_rgb(0, 0, 0)
  context.rectangle(0, 0, size, size)
  context.stroke
  context.set_source_rgb(1, 0, 0)
  q.each do |qi|
    context.arc(qi.x,qi.y,2,0,2.0*Math::PI)
    context.fill
  end
  if tree!=nil
    mkey.each do |key|
      tree.draw(key,context)
    end
  end
  surface.write_to_png(filename)
end

結局メインルーチンはこうなる。

Particle = Struct.new(:x, :y)
srand(2)
L = 256.0
q = []
10.times do
  x = L*rand
  y = L*rand
  q.push Particle.new(x, y)
end

mkey = Array.new(q.size)
tree = BHTree.new(L)

q.size.times do |i|
  tree.add(0,i,mkey,q)
end

save_png("initial.png",L, q, mkey, nil)
save_png("barnes-hut.png",L, q, mkey, tree)

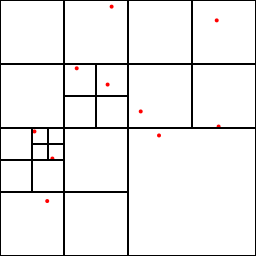
実行結果。

• initial.png

• barnes-hut.png

できているみたいですね。

まとめ

モートンキーを使ったBarnes-Hut treeの構築をしてみた。正確には、まだ木は作ってないので、このキーを使ってちゃんと木を作ってから当たり判定だの力の計算だのをすることになるんだと思う。また、ゲーム用途とかで速度を気にするならいろいろ書き直さないとダメかも。っていうか多分もっと効率的な木の作り方がきっとあるので、興味のある人は調べてください。

参考URL

• その８ 4分木空間分割を最適化する！（理屈編） 線形4分木についてはここが一番わかりやすかった。
• Note on Parallel Tree Code 中里さんによるツリーコードのまとめ

1. 一般的な呼び方かどうかは知らない。 ↩

2. 木を表現するクラスではないので、あまり適切な名前では無い気がする。線形4分木をハッシュで表現するクラスなので、そういう名前の方が良いかも。 ↩