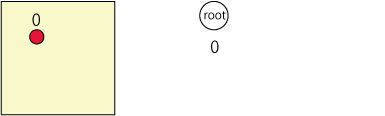はじめに

わけあって、重力多体系の計算で使われるBarnes-Hut treeを構築することになったので覚書。

コードは
https://github.com/kaityo256/barnes-hut
に置いてある。

Barnes-Hut treeとは

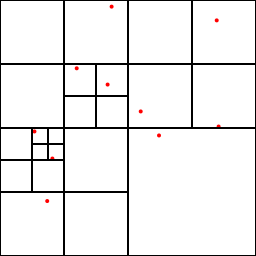
空間と粒子の座標が与えられた時、空間を再帰的に分割していって、分割された部分空間に粒子がたかだか一個しか入らないようにする。例えば二次元空間なら、もし粒子が2個以上入っていたらその空間を4分割、分割した空間にまだ粒子が2個以上いたら空間を4分割…と再帰的に分割していく。3次元なら8分割になる。こうしてできた構造は木(tree)になる。

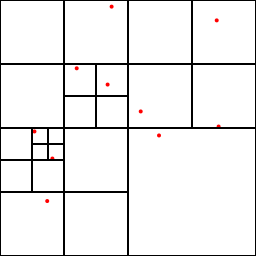
例えばこういう空間と粒子配置が与えられた時に、

こんな感じに分割してやりたい。

元論文では構成した木を利用して重力計算を行うのだが、ここでは単にBarnes-Hut treeの構築方法を考える。

構築アルゴリズム

ここの解説が詳しいというか、これを読むだけなのだが、もう少し詳細に書いてみる。

まず、ノードとは、以下の条件を満たすものである。

ノードは、部分空間を担当している。
ノードは、「粒子がいない」「粒子が一個だけいる」「粒子が二個以上いる」の三通りの状態がある
粒子が二個以上いるノードは、担当する空間が4分割され、それぞれを子ノードが担当している

ノードの状態が三通りあるので、そこに粒子を追加しようとすると、三通りの処理が必要になる。

粒子がいない場合：単に粒子を追加すれば良い
粒子が一個だけいる場合：自分を四分割し、もともといた粒子と、追加された粒子をそれぞれ子ノードに追加する
粒子が二個以上いる場合：追加された粒子を子ノードに渡す

以下は例。

まず、系全体を担当する空のrootノードを用意する。

粒子を順番に追加していく。まずは0番の粒子。この時rootノードは粒子がいない状態なので、受け取った粒子を追加する。

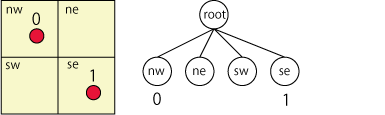
次に1番の粒子をrootノードに渡す。rootノードは粒子が二つ目となるので、まず自身を4分割し、それぞれを担当するノードを作る。。その上で、元々持っていた粒子0番と、今回受け取った粒子1番を、それぞれ受け持つべきノードに渡す。この場合は0番を「北西(nw)」を担当するノードに、1番を「南東(se)」を担当するノードに渡す。

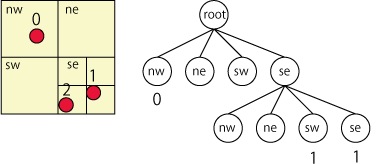
次に2番の粒子をrootノードに渡す。rootノードは、既に自身が4分割されているので、担当すべき子ノード(この場合は南東(se)ノード)に2番の粒子を渡す。南東のノードは既に粒子を持っているので、自身を4分割し、もともと持っていた粒子1番と、今回うけとった粒子2番をそれぞれ担当すべき子ノードに渡す。今回のケースでは、1番を南西(sw)ノードに、2番を南東(se)ノードに渡した。

このように、rootノードに粒子の追加依頼をすると、後は再帰的に上記の処理を繰り返し、分割が完了する。

実装

あとでC++に移植する都合から、粒子座標の配列と、粒子番号をノードに渡して追加していく形にする。¹

粒子の座標は、とりあえずこんな感じで用意しよう。

Particle = Struct.new(:x, :y)
srand(2)
L = 256.0
q = []
10.times do
  x = L*rand
  y = L*rand
  q.push Particle.new(x, y)
end

とりあえず正方形しか考えないことにすると、ノードクラスNodeが保持すべき領域は、一辺の長さと、左上の座標で決まる。なので、コンストラクタはサイズとx,y座標を渡す形になるだろう。

root = Node.new(L, 0.0, 0.0)

そして、粒子情報をルートノードrootに渡すと、あとはよしなに分割していく形が望ましい。

q.size.times do |i|
  root.add(i, q)
end

この、コンストラクタとaddを実装すれば良い。

まずコンストラクタは、単に必要な情報を初期化すれば良いので、こんな感じかな。

class Node
  def initialize(size, x, y)
    @size = size
    @x = x
    @y = y
    @myparticle = -1
    @nodes = []
  end
end

それぞれ、一辺の長さが@size、左上の座標が@x, @y、そして自分が担当する領域に粒子が一つしかいなかった場合の粒子番号が@myparticle(いない場合は-1)、子ノードを保持する配列が@nodes。

次に、粒子を追加するメソッドaddは、先に説明したアルゴリズムをそのまま実装すればいい。

  def add(i, q)
    if @nodes.size != 0
      add_sub(i, q)
    elsif @myparticle !=-1
      hs = @size*0.5
      @nodes.push Node.new(hs, @x, @y)
      @nodes.push Node.new(hs, @x+hs, @y)
      @nodes.push Node.new(hs, @x, @y+hs)
      @nodes.push Node.new(hs, @x+hs, @y+hs)
      add_sub(@myparticle, q)
      add_sub(i, q)
      @myparticle = -1
    else
      @myparticle = i
    end
  end

それぞれ、

子ノードがいる場合は子ノードに粒子を渡すメソッドadd_subを呼ぶ
子ノードが無く、自分が粒子を持っていた場合は、自分を4分割し、自分が持っていた粒子(@myparticle)と、いま受け取った粒子iについてそれぞれ子ノードに粒子を渡すメソッドadd_subを呼ぶ
自分が空ノードの場合は、粒子を保持する

という感じ。

子ノードに粒子を渡す関数add_subは、粒子が4分割した領域のどこにいくべきか調べて、対応するノードのaddを呼べば良い。

  def add_sub(i, q)
    hs = @size*0.5
    ix = ((q[i].x - @x)/hs).to_i
    iy = ((q[i].y - @y)/hs).to_i
    id = ix + iy * 2
    @nodes[id].add(i, q)
  end

以上を全部まとめると、ノードクラスはこんなコードになる。

class Node
  def initialize(size, x, y)
    @size = size
    @x = x
    @y = y
    @myparticle = -1
    @nodes = []
  end

  def add_sub(i, q)
    hs = @size*0.5
    ix = ((q[i].x - @x)/hs).to_i
    iy = ((q[i].y - @y)/hs).to_i
    id = ix + iy * 2
    @nodes[id].add(i, q)
  end

  def add(i, q)
    if @nodes.size != 0
      add_sub(i, q)
    elsif @myparticle !=-1
      hs = @size*0.5
      @nodes.push Node.new(hs, @x, @y)
      @nodes.push Node.new(hs, @x+hs, @y)
      @nodes.push Node.new(hs, @x, @y+hs)
      @nodes.push Node.new(hs, @x+hs, @y+hs)
      add_sub(@myparticle, q)
      add_sub(i, q)
      @myparticle = -1
    else
      @myparticle = i
    end
  end

end

組む前はわりと悩んだんだけど、できてみたらすごい簡単だった。

描画

組んだ後、ちゃんとできてるかどうか描画したい。Rubyだとcairo使うのが簡単かな。こんな関数を書いてみる。

def save_png(filename, size, q, root)
  surface = Cairo::ImageSurface.new(Cairo::FORMAT_RGB24, size, size)
  context = Cairo::Context.new(surface)
  context.set_source_rgb(1, 1, 1)
  context.rectangle(0, 0, size, size)
  context.fill
  context.set_source_rgb(0, 0, 0)
  context.rectangle(0, 0, size, size)
  context.stroke
  context.set_source_rgb(1, 0, 0)
  q.each do |qi|
    context.arc(qi.x,qi.y,2,0,2.0*Math::PI)
    context.fill
  end
  root.draw(context)
  surface.write_to_png(filename)
end

ファイル名、系のサイズ、座標の配列、ルートノードを受け取って描画する関数。ノードクラスのDrawメソッドは、単に自分が4分割されていたら、分割線を描画するメソッド。こんな感じ。

class Node
  def draw(context)
    return if @nodes.size == 0
    context.set_source_rgb(0, 0, 0)
    hs = @size*0.5
    context.move_to(@x + hs, @y)
    context.line_to(@x + hs, @y+@size)
    context.move_to(@x , @y + hs)
    context.line_to(@x + @size, @y+hs)
    context.stroke
    @nodes.each do |t|
      t.draw(context)
    end
  end
end

粒子を追加しおわった状態で以下のように呼んでやる。

save_png("barnes-hut.png", L, q, root)

するとこんなファイルができる。

まとめ

重力多体系の力の計算に使われるBarnes-Hutアルゴリズムで用いられる、Barnes-Hut treeを構築してみた。今回は二次元版を組んだけど、addの中の分割と、add_subのインデックス計算のところだけ書き換えれば、3次元版への拡張はすぐだと思う。

ほとんどここの解説そのままなんだけど、粒子を保持していない時の状態と、分割のタイミングがちょっと違う？また、今回は木を構築しただけなので、その後の計算に扱いやすいデータ構造になってるかどうかわからない。構築の計算コストは平均的には$O(N \log N)$だと思うけど、最悪計算量は$O(N^2)$になるのかな？²

あと、ノードの状態を「空」「粒子一個」「粒子二個以上」の三状態に分けたけど、それが最適かどうかはわからない。特に@myparticleが-1かどうか判定しているところが美しくないんだけれど、自分が保持する粒子数を持つにせよ、フラグで管理するにせよ、いずれにせよ粒子番号を保持する必要はあるので、これでいいのかなぁ。

参考文献

The Barnes-Hut Algorithm これが一番わかりやすい解説だった。
J. Barnes & P. Hut, Nature. 324 (4): 446–449. A hierarchical O(N log N) force-calculation algorithm Natureに掲載された元論文。

C++のコードのプロトタイピングのつもりなのでこうなっているが、ただRubyで組むだけなら、粒子番号ではなく、粒子の座標情報をそのまま保持するほうがきれいな気がする。 ↩
常に最下層のノードの同じパネル(例えばsw)に追加し続けるような場合。 ↩