Go to Qiita Advent Calendar 2024 Top
LoginSignup
18
16

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@mitchiinaga

SPH法の理論と実装 ~理論編2~

Posted at

SPH法の理論と実装 ~理論編1~の続きです。ちょっと応用的な内容になります。

SPH法と接触不連続面

理論編1の終わりで、SPH法では接触不連続面で非物理的な圧力勾配力が発生してしまうと述べました。これは以下のように説明できます。

SPH法では、密度は

\rho_i = \sum_j m_j W_{ij}(h_i)

で計算されるため、あらゆる場所で連続的になります。一方で、エネルギー方程式を時間積分して計算される内部エネルギーは、密度と比べると不連続性を保ち続けます。そして、圧力は状態方程式
$$
p_i = (\gamma - 1) \rho_i u_i
$$
を使って計算されるので、接触不連続面で密度、内部エネルギー、圧力は以下の図のようになります。横軸は適当な座標軸です。
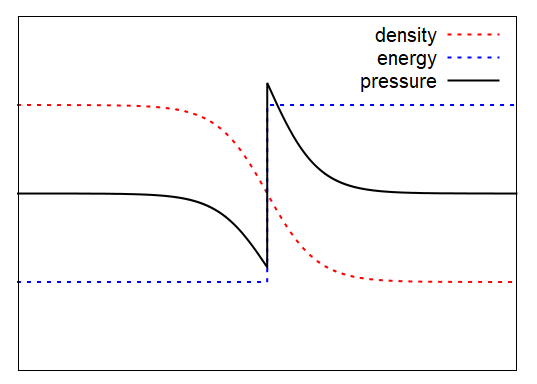
surface.png
この圧力ジャンプによって、接触不連続面で本来発生するはずのない圧力勾配力が発生してしまいます。
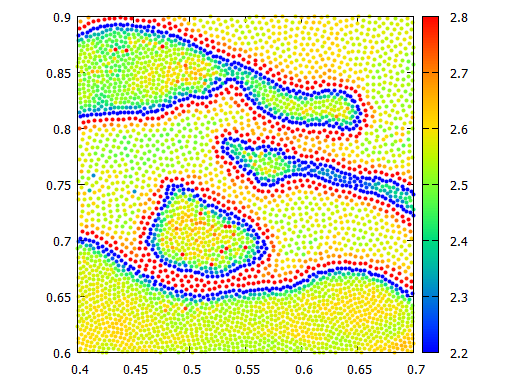
khi_pressure.png
理論編1のKH (Kelvin-Helmholtz)不安定性シミュレーションの圧力分布をカラーマップで示したのが上の図です。実際に、高密度領域と低密度領域の境界で圧力が不連続的になってしまっているのがわかると思います。

人工熱伝導 (Artificial Thermal Conductivity)

この問題に対する処方箋として、エネルギー方程式に拡散項を加え、密度と同様に滑らかにしてやるという方法があります。この拡散項を人工熱伝導と呼びます。Price (2008)では

\left( \frac{d u_i}{dt} \right)_{\rm AC} = - \alpha_{\rm u} \sum_j \frac{2 m_j}{\rho_i + \rho_j} v_{ij}^{\rm sig, u} (u_i - u_j) \frac{\boldsymbol{r}_i - \boldsymbol{r}_j}{|\boldsymbol{r}_i - \boldsymbol{r}_j|} \cdot \bar{W}_{ij},

という式をエネルギー方程式に追加して、接触不連続面で発生してしまっていた非物理的な圧力勾配を抑えることに成功しています。係数 $\alpha_{\rm u}$ や $v_{ij}^{\rm sig, u}$ の与え方にはいくつか選択肢があるのですが、例えば、Price et al. (2018)では、

\alpha_{\rm u} = 1,\\
v_{ij}^{\rm sig, u} =\begin{cases}
\sqrt{\frac{2|p_i - p_j|}{\rho_i + \rho_j}} & {\rm w/o\; gravity}\\
\left| (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot \frac{\boldsymbol{r}_i - \boldsymbol{r}_j}{|\boldsymbol{r}_i - \boldsymbol{r}_j|} \right| & {\rm w/\; gravity}
\end{cases},

としています。

Density Independent SPH (DISPH)

人工熱伝導を入れることで接触不連続面でスムーズな圧力分布が得られるようになりますが、$\alpha_{\rm u}$ や $v_{ij}^{\rm sig, u}$ のような人工的なパラメータの調整が必要になってきます。
接触不連続面の問題を、人工熱伝導無しで解決できる手法としてDensity Independent SPH (DISPH)法があります (Saitoh & Makino 2013; Hopkins 2013)。

これ以降では、DISPH法と区別するために、理論編1で導出したSPH法をStandard SPH (SSPH)法と呼ぶことにします。
SSPH法では体積積分を離散化式に置き換えるときの微小体積を

\Delta V_i = \frac{m_i}{\rho_i},\\
\rho_i = \sum_j m_j W_{ij}(h_i),

としていました。実は、この微小体積の与え方は、任意の物理量 $y, Z$ を使って

\Delta V_i = \frac{Z_i}{y_i},\\
y_i = \sum_j Z_j W_{ij},\\

と一般化することができます。これをうまく使って、数式に密度が現れないようにすることで接触不連続面の問題を解決したのがDISPH法です。

以下、Hopkins (2013)の方程式を紹介します。理想気体の状態方程式を使うと $y = p, Z = (\gamma - 1) m u$として、微小体積が

\Delta V_i = (\gamma - 1) \frac{m_i u_i}{p_i},\\
p_i = (\gamma - 1) \sum_j m_j u_j W_{ij}(h_i),

と書けます。これに拘束条件として

n_i h_i^d = {\rm const.},\\
n_i = \sum_j W_{ij}(h_i),

を与えてオイラーラグランジュ方程式を解くと、運動方程式

\frac{d \boldsymbol{v}_i}{dt} = - (\gamma - 1)^2 \sum_j m_j u_i u_j \left[ \frac{f_{ij}}{p_i} \nabla W_{ij}(h_i) + \frac{f_{ji}}{p_j} \nabla W_{ij}(h_j) \right],\\
f_{ij} = 1 - \left[ \frac{h_i}{d(\gamma - 1) n_i m_j u_j} \frac{\partial p_i}{\partial h_i} \right]
\left( 1 + \frac{h_i}{n_i d} \frac{\partial n_i}{\partial h_i} \right)^{-1},

が得られます。エネルギー方程式は

\frac{d u_i}{dt} = (\gamma - 1)^2 \sum_j m_j u_i u_j \frac{f_{ij}}{p_i} (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot \nabla W_{ij}(h_i),

となります。

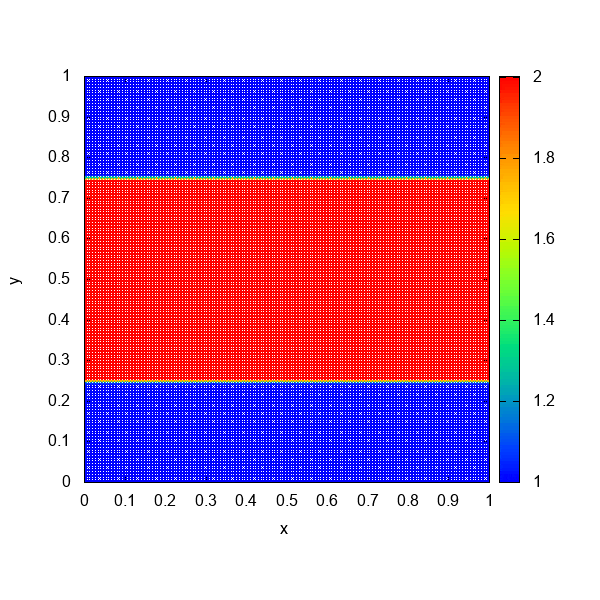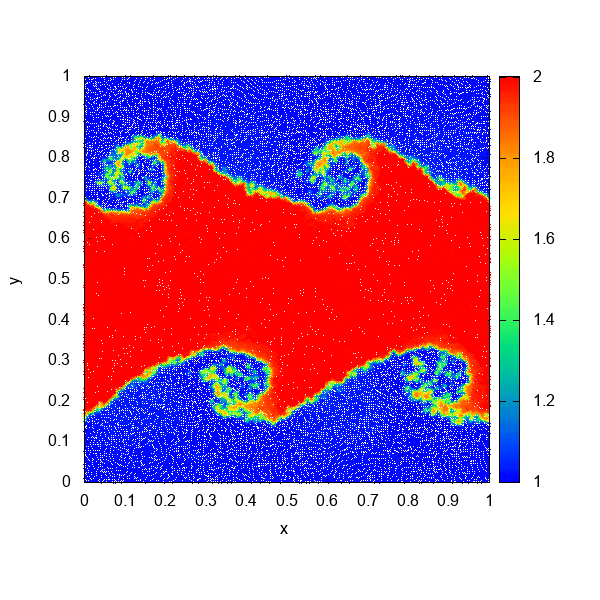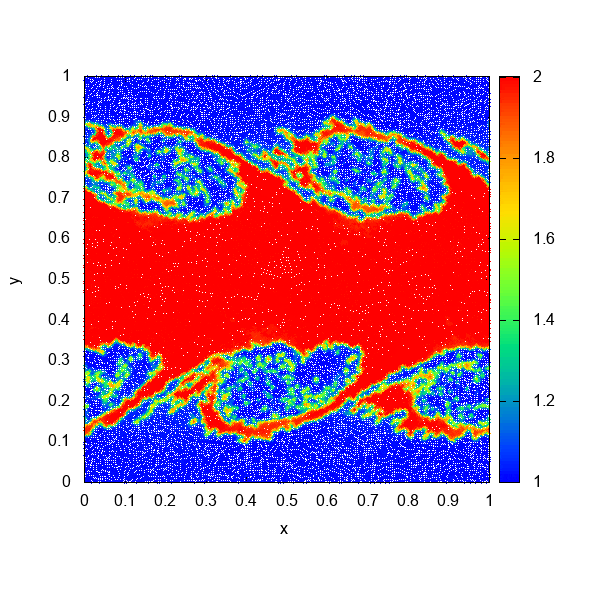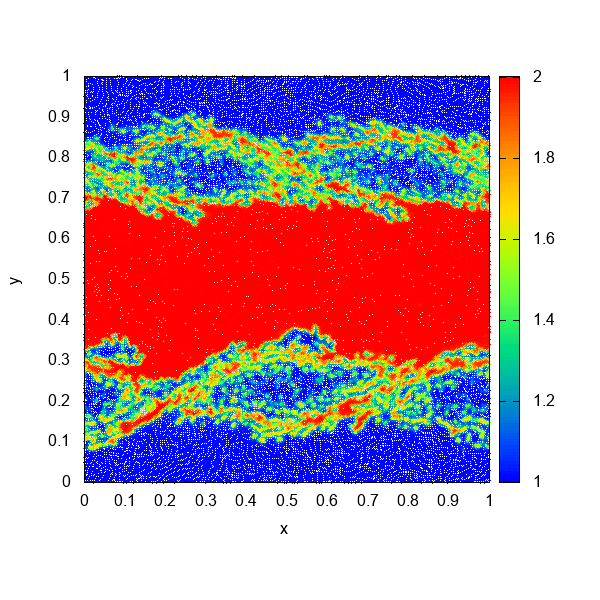
khi_di.gif
これがDISPH法を使ってKH不安定性を解いた結果です。SSPH法のときに二層の間に働いていた表面張力のような力が取り除かれ、流体が混合していくような挙動が確認できるようになりました。

DISPH法でも、衝撃波を解くためには人工粘性は入れる必要があります。人工粘性項に現れる密度は $\rho_i = \sum_j m_j W_{ij} (h_i)$ で計算したほうがよいということが経験的に知られています (Saitoh & Makino 2013)。

Godunov SPH (GSPH)

人工粘性や人工熱伝導が無くても衝撃波や接触不連続面が扱える手法があります。それがGodunov SPH (GSPH)法です (Inutsuka 2002; Cha & Whitworth 2003; Iwasaki & Inutsuka 2011)。
GSPH法は、衝撃波管問題を一般化したRiemann問題の解を、SPH法の方程式に組み込んだものです。Riemann問題は有限体積法でメッシュ境界の物理量を算出するときによく使われるのですが、それと同様にGSPH法では粒子と粒子の間の位置の物理量をRiemann問題で求めて相互作用計算に使います。

サンプルコードには Cha & Whitworth (2003)のGSPH法を実装しています。これはInutsuka (2002)より簡単な方程式となっていますが、その代わりに数値粘性が若干多めに入ってしまいます。具体的な数式は以下になります。

\frac{d \boldsymbol{v}_i}{dt} = -\sum_j m_j p_{ij}^* \left[ \frac{1}{\rho_i} \nabla W_{ij}(h_i) + \frac{1}{\rho_j} \nabla W_{ij}(h_j) \right],\\
\frac{d u_i}{dt} = -\sum_j m_j p_{ij}^* (\boldsymbol{v}_{ij}^* - \boldsymbol{v}_i) \cdot \left[ \frac{1}{\rho_i} \nabla W_{ij}(h_i) + \frac{1}{\rho_j} \nabla W_{ij}(h_j) \right].

*がついた物理量をRiemann solverで求めます。

その他

これまでに紹介した以外で押さえておくべき内容についていくつか書きます。

エントロピー方程式

エネルギー方程式の代わりに、エントロピー方程式を使って計算することも可能です (e.g. Springel & Hernquist 2002; Hopkins 2013)。圧力と密度がポリトロピック関係式
$$
p = A \rho^\gamma
$$
で書けるとします。係数 $A$ はエントロピーにのみ依存する物理量で、衝撃波などによるエントロピー生成のみ考えてやればいいので、
$$
\frac{dA_i}{dt} = \frac{\gamma - 1}{\rho_i^{\gamma - 1}} \left( \frac{du_i}{dt} \right)_{\rm AV}
$$
という式で計算できます。人工粘性以外に人工熱伝導などを加える場合は、それらも考慮する必要があります。

エントロピー方程式を使うメリットとしては、エントロピー増大則やエネルギーの非負性を確実に満たすようにできるなどがあります。

人工粘性

Cullen & Dehnen (2010)では人工粘性を制御するために、速度の発散の時間微分を使う手法を提案しています。式は理論編1で紹介したものより煩雑になりますが、これによって衝撃波の前面と後面の区別が付けられるようになっています。

Hosono et al. (2013)では、Monaghan (1997)のような2粒子間モデルの人工粘性ではなく

q_i = -\alpha_i \rho_i c_i h_i \nabla \cdot \boldsymbol{v}_i + \beta_i \rho_i h_i^2 \left( \nabla \cdot \boldsymbol{v}_i \right)^2

を人工圧力として加えるvon Neumann-Richtmyer-Landshoff型の人工粘性を使って、Keplerian Diskのテストを行っています。これを使うことで、流体の差動回転を2粒子間モデル型の何倍も長持ちさせることに成功しています。

Monaghan (2005)では2粒子間モデルの人工粘性 (Monaghan & Gingold 1983; Monaghan 1999と性能はほぼ同じ) がどの程度の粘性として働いているのか述べられています。この論文によると、せん断粘度、体積粘度がそれぞれ $\eta = \alpha \rho c h / (2d + 4), 5 \eta / 3$ と見積もられています。ここで、$d$ は次元を表します。

pairing instability

理論編1のカーネル関数の箇所で簡単に触れたpairing instabilityについて、どのような不安定性なのか紹介します。

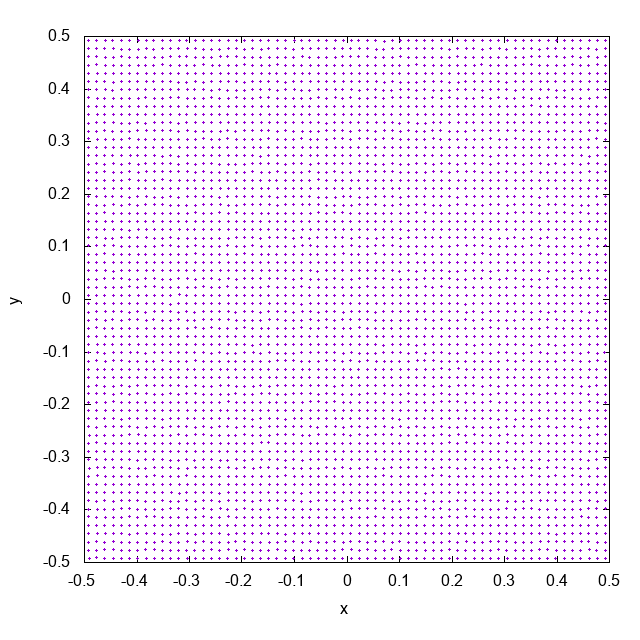
2次元系で、上図のようにSPH粒子を配置します。これは、格子状に粒子を置いたあと、一様乱数を使って格子幅の5 %以下だけ粒子を動かしています。
$t = 0$ で全粒子の速度を0、圧力を一定とし、シミュレーションを進めると以下のようになります。

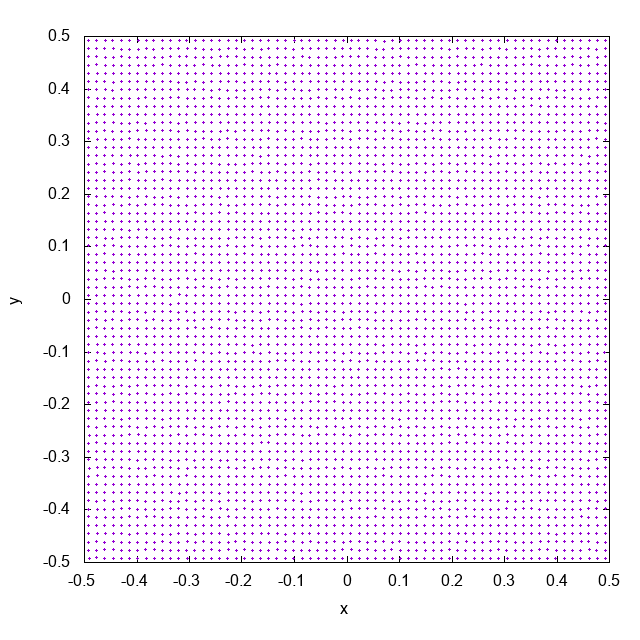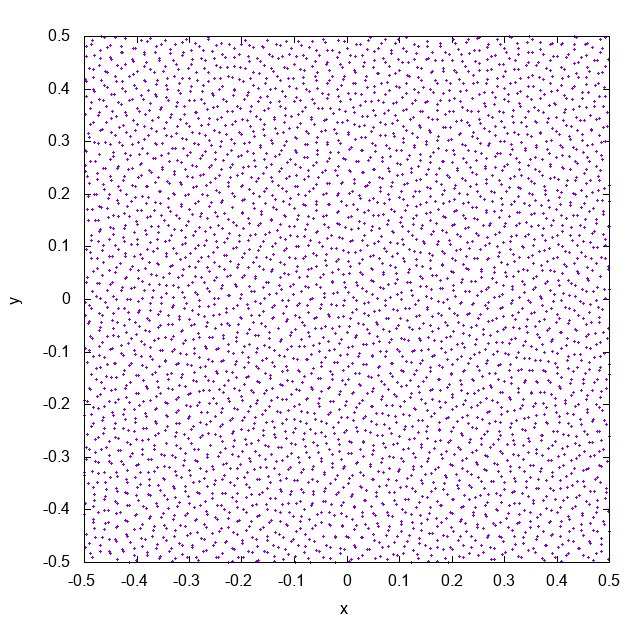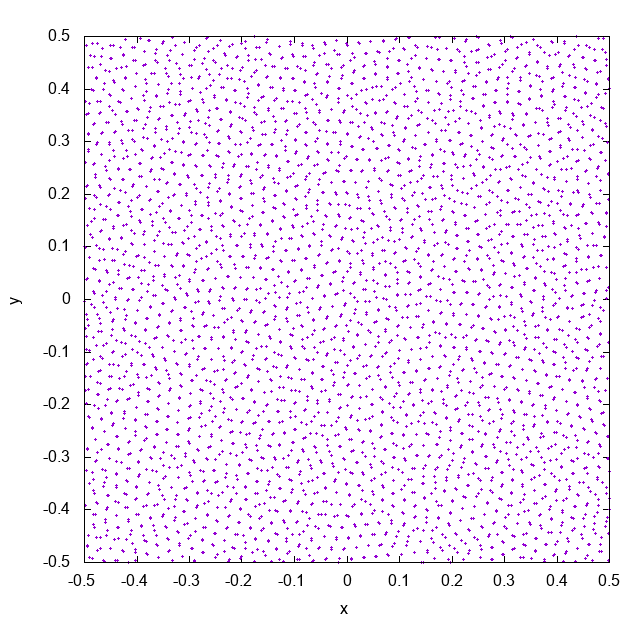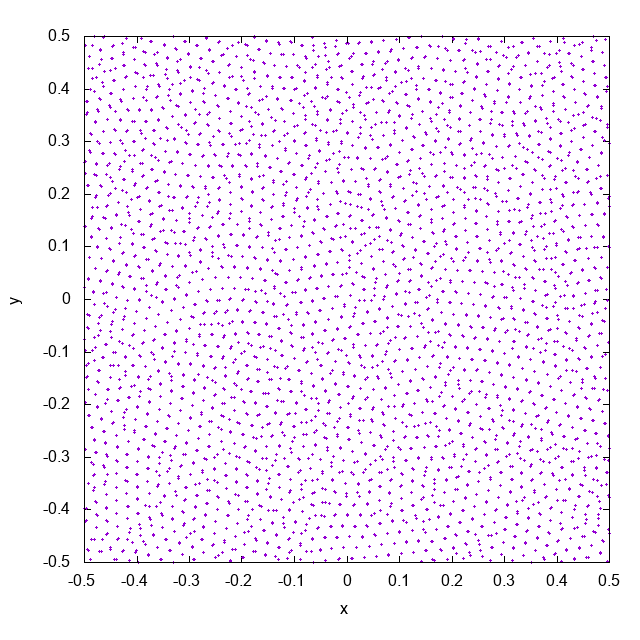
これは近傍粒子数がおよそ32個になるようにして ($\rho h^2 / m = 32$ でsmoothing lengthを決めています)、cubic spline関数をカーネルとして使って計算した結果です。徐々に粒子同士がくっついていってしまっています。これがpairing instabilityと呼ばれる現象です。pairing instabilityによって、複数の粒子が同じ場所に位置するようになり、実効的な解像度が下がってしまします。

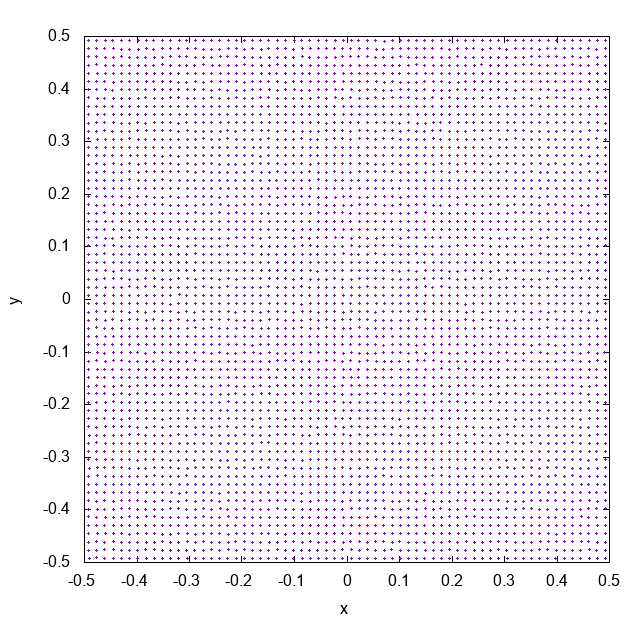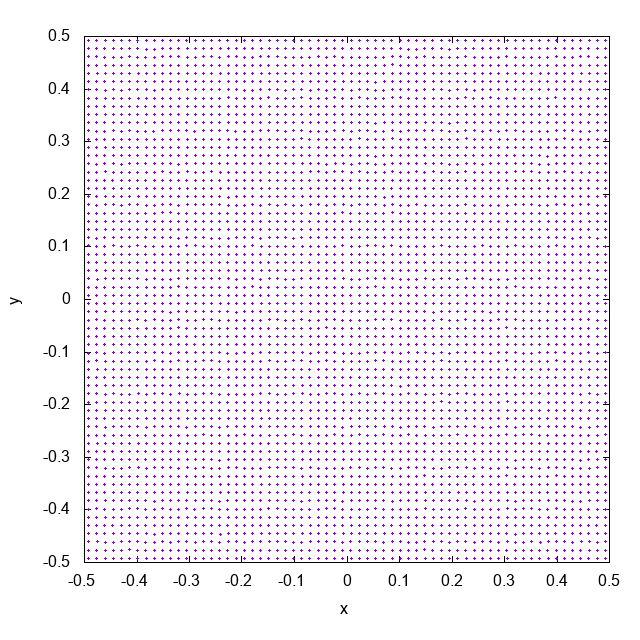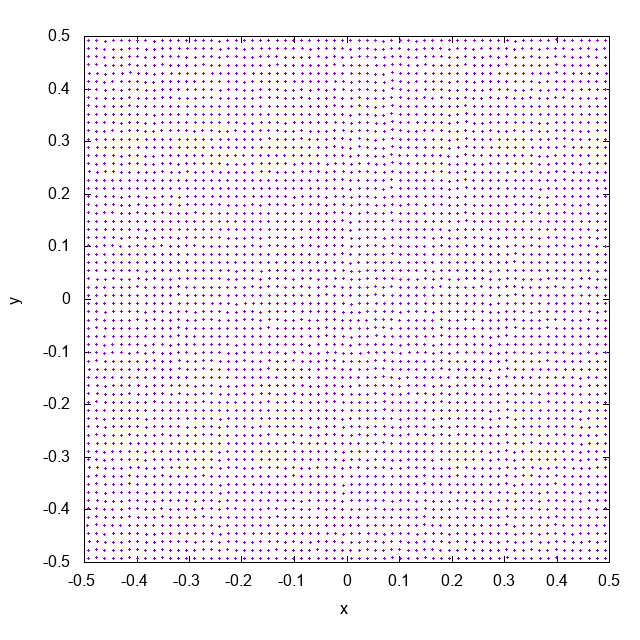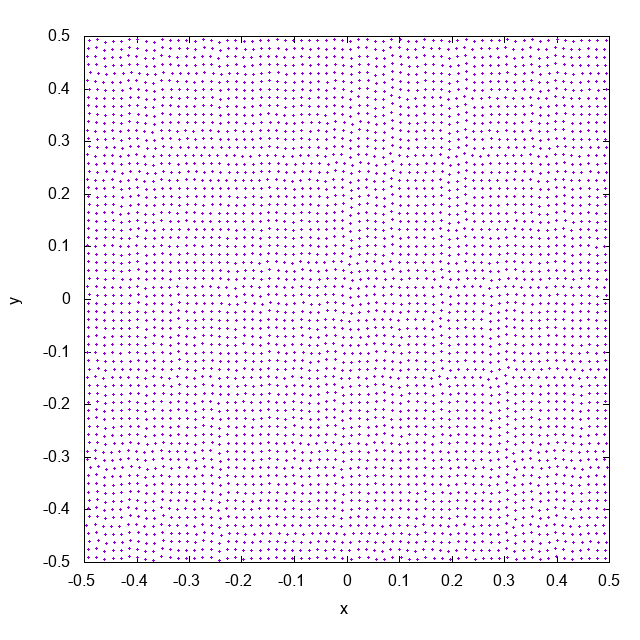
近傍粒子数も含め、同条件でWendlandカーネルで計算した結果がこちらです。cubic spline関数のときと異なり、粒子配置が非常に安定しています (もちろん1フレームあたりの時間や、計算終了時刻はどちらのシミュレーションも同じです。アニメーションに時刻を入れるのを忘れていました)。

pairing instabilityが発生する原因は、SPH法で一般的に用いられるカーネル関数の形状に原因があります。SPH法の運動方程式に登場するカーネル関数の1回微分は、ガウス関数のような形をしているため

 | \lim_{r \rightarrow 0} \nabla W(r,h) | = 0

となります。つまり、2粒子間の距離が非常に小さくなったときに相互作用が働かなくなってしまいます。これがpairing instabilityの原因です。

なぜWendlandカーネルに変更することでpairing insabilityを回避できたかについてですが、「同じ影響半径 (≠ smoothing length)のときに、Wendlandカーネルの方が $r=0$ 近傍で尖っているから」と大雑把に理解することができます (下図参照。2次元の場合)。詳細について知りたい場合はDehnen & Aly (2012)を参照してください。
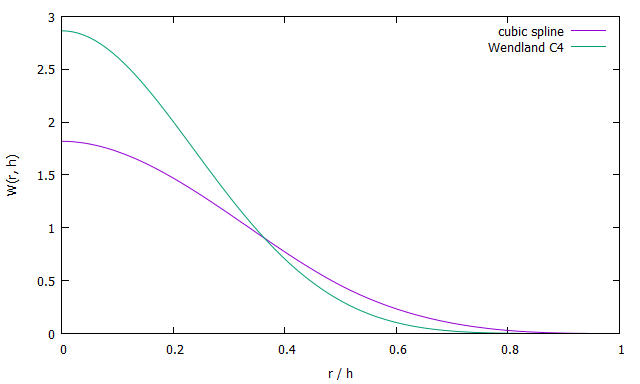
image.png

なお、同様にSPH粒子がくっついて離れなくなる不安定性としてtensile instabilityがあります。tensile instabilityは、負圧によって粒子同士に引力が働く場合に発生します。従って、今回記事で紹介する範囲では関係ありませんが、MHDや自由表面流れの場合は何らかの処方箋を考える必要があると思われます。

最後に

理論編はとりあえずこれで終わりとします。紹介したDISPH法やテスト計算などは https://github.com/mitchiinaga/sphcode に実装しています。
次は実装編として、時間積分や近傍粒子探索などについて書こうと思います。記事を上げるまでちょっと時間がかかるかもしれませんが、よろしくお願いします。

参考文献

18
16
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
18
16

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?