LoginSignup
47
36

More than 3 years have passed since last update.

@mitchiinaga

SPH法の理論と実装 ~理論編1~

Last updated at Posted at 2019-06-23

SPH法とは

SPH (Smoothed Particle Hydrodynamics)法とは、Lucy (1977)とGingold & Monaghan (1977)によって開発された流体の計算法です。「粒子法」と呼ばれる計算法の1つで、流体を粒子によって離散化し、その運動をラグランジュ的に追跡します。
SPH法はもともと宇宙物理学の分野で圧縮性流体を解くために開発された計算法ですが、弾性体や非圧縮性流体の解析にも応用され、CAEやCGといった幅広い分野で活用されるようになっています。SPH法の使用事例としては、次の動画のようなものがあります。

なお、本記事で取り扱うのは圧縮性流体用のSPH法です。

SPH法の長所としては、次のようなものがあります。

  • 質量密度とSPH粒子の数密度が対応関係にあるため、高密度領域が自動的に高解像度となる。
  • 方程式がガリレイ不変性を持つ。
  • 移流による数値拡散が発生しない。
  • (AMRなどと比べると) 実装が簡単。自己重力も2対相互作用で簡単に実装できる。
  • 質量、エネルギー、運動量、角運動量 (非粘性の場合)が保存する。

逆に、短所は

  • 低密度領域が低解像度
  • 工夫しないと計算コストが大きい。
  • 人工粘性を入れないと衝撃波が扱えない。
  • 方程式が適合性 (consistency)を満たさず、粒子の分布によっては計算精度が著しく低下する。

などがあります。

SPH法のコンセプト

物理量の補間

ディラックのデルタ関数を使うと、位置 $\boldsymbol{r}$ での物理量 $F$ は
$$
F(\boldsymbol{r}) = \int F(\boldsymbol{r}') \delta(|\boldsymbol{r} - \boldsymbol{r}'|) dV',
$$
と書けます。ここで、 $h \rightarrow 0$ で $W(r,h) \rightarrow \delta(r)$ となるような関数を使って
$$
F(\boldsymbol{r}) \simeq \int F(\boldsymbol{r}') W(|\boldsymbol{r} - \boldsymbol{r}'|, h) dV',
$$
と近似できるとします。さらに、質量 $m$ と密度 $\rho$ から $dV \sim m / \rho$ と近似し、 $\int$ を $\sum$ で置き換えると

F_i = \sum_j \frac{m_j}{\rho_j} F_j W_{ij},

という離散化式が得られます。ここで、$F_i$ は $\boldsymbol{r}_i$ に位置する $i$ 番目の粒子の物理量 $F$ を表します。また、 $W_{ij} \equiv W(|\boldsymbol{r}_i - \boldsymbol{r}_j|, h)$ とします。これに $F = \rho$ を代入すると、密度の計算式
$$
\rho_i = \sum_j m_j W_{ij},
$$
が得られます。初期条件に合わせてあらかじめ粒子の質量を与えておくと、補間関数 $W(r,h)$ を使って任意の位置における物理量の近似値が計算できるようになりました。

次に物理量 $F$ の空間微分も同様の畳み込み積分の形で書けるとすると、

\begin{align}
\nabla F(\boldsymbol{r}) &\simeq \int \nabla' F(\boldsymbol{r}') W(|\boldsymbol{r} - \boldsymbol{r}'|, h) dV',\\
&= -\int F(\boldsymbol{r}') \nabla' W(|\boldsymbol{r} - \boldsymbol{r}'|, h) dV',\\
&= \int F(\boldsymbol{r}') \nabla W(|\boldsymbol{r} - \boldsymbol{r}'|, h) dV',\\
\nabla_i F_i &\simeq \sum_j \frac{m_j}{\rho_j} F_j \nabla_i W_{ij},
\end{align}

となります。これによって、任意の位置における物理量の微分値も計算できるようになりました。

カーネル関数

上の数式に現れる関数 $W(r,h)$ はカーネル関数と呼ばれています。一般的に、カーネル関数にはガウス関数のような釣鐘型の関数が使われます。カーネル関数の例として、cubic spline関数 (e.g. Monaghan 1992)

\begin{align}
W(r,h) = \frac{\sigma}{h^d}
\begin{cases}
1 - \frac{3}{2} q^2 + \frac{3}{4} q^3 & (0 \leq q < 1)\\
\frac{1}{4} (2 - q)^3 & (1 \leq q < 2)\\
0 & (q \geq 2)
\end{cases},
\end{align}

や、Wendlandカーネル (Wendland 1995)

\begin{align}
W(r,h) = 
\begin{cases}
\frac{\sigma}{h^d} (1 - q)^6 \left( 1 + 6q + \frac{35}{3} q^2 \right)  & (0 \leq q < 1)\\
0 &  (q \geq 1)
\end{cases}
\end{align}

があります。ここで $q = r/h$、 $d$ は次元、 $\sigma$ は規格化定数です。 $\sigma$ はカーネル関数が満たすべき規格化条件
$$
\int W(|\boldsymbol{r}|,h) dV = 1,
$$
を満たすように与えられます。$h$ は計算の空間解像度や粒子が相互作用する範囲に関わるパラメータで、smoothing lengthと呼ばれています。圧縮性解法ではsmoothing lengthは相互作用する近傍粒子の数が (厳密に or おおよそ)一定になるように毎ステップ更新するのが一般的です。

カーネル関数は上で紹介した以外にも様々な関数形が提案されており、計算条件に合わせて適切な関数を選ぶことが重要です。
例えば、相互作用させる近傍粒子の数が少ない場合はcubic spline関数を使えば問題ありませんが、ある一定数を超えると、粒子同士がくっついて離れなくなってしまうというSPH法特有の数値不安定性 (pairing instability; Dehnen & Aly 2012)が発生するようになってしまいます。この問題は、Wendlandカーネルのようなより高次の関数を使うことで回避できます。

流体方程式

運動方程式

物理量の微分値を計算式は上で導出したので、これを流体の運動方程式 (Euler方程式)
$$
\frac{d \boldsymbol{v}}{dt} = -\frac{1}{\rho} \nabla p,
$$
に適用すれば、SPH粒子の運動を司る方程式が導出できます。

一方、流体のラグランジアンを離散化し、変分原理から方程式を導出するという方法も提案されています (Springel & Hernquist 2002; Monaghan 2002)。圧縮性SPHにおいては多分こちらが主流です。変分原理から導出する場合、smoothing lengthを可変にしたときに運動方程式に加えるべき補正項を簡単に求めることができます。
流体のラグランジアンは
$$
L = \int \rho \left( \frac{\boldsymbol{v}^2}{2} - u \right) dV,
$$
と書けるので、$dV \sim m / \rho$ とすると、ラグランジアンは
$$
L = \sum_i \left( m_i \frac{\boldsymbol{v}^2_i}{2} - m_i u_i \right),
$$
と離散化できます。ここで、$u$ は流体の内部エネルギーを表します。また、密度は

\rho_i = \sum_j m_j W_{ij}(h_i),\\
W_{ij}(h_i) \equiv W(|\boldsymbol{r}_i - \boldsymbol{r}_j|, h_i),

で計算するとします。さらに、粒子 $i$ の影響半径内の粒子数を一定にするという拘束条件
$$
\frac{\rho_i}{m_i} h_i^d = {\rm const.},
$$
を与えて、オイラーラグランジュ方程式を計算すると、運動方程式

\frac{d \boldsymbol{v}_i}{dt} = - \sum_j m_j \left[ f_i \frac{p_i}{\rho_i^2} \nabla W_{ij}(h_i) + f_j \frac{p_j}{\rho_j^2} \nabla W_{ij}(h_j) \right],\\
f_i = \left( 1 + \frac{h_i}{\rho_i d} \frac{\partial \rho_i}{\partial h_i} \right)^{-1},

が得られます。詳しい導出は Springel & Hernquist (2002) などを参照してください。

Euler-Lagrange 方程式からSPH法の運動方程式を求める - Qiita
こちらの記事に少し詳しく書きました。

エネルギー方程式

smoothing length $h_i$ の微分に注意して $\rho_i = \sum_j m_j W_{ij}(h_i)$ を時間微分すると、連続の式

\frac{d \rho_i}{dt} = f_i \sum_j m_j \left( \boldsymbol{v}_i - \boldsymbol{v}_j \right) \cdot \nabla W_{ij}(h_i),

が得られます。また、断熱過程では、内部エネルギーの時間変化と連続の式との間に
$$
\frac{d u}{dt} = \frac{p}{\rho^2} \frac{d \rho}{dt},
$$
という関係が成り立ちます。従って、エネルギー方程式は

\frac{du_i}{dt} = f_i \frac{p_i}{\rho_i^2} \left( \boldsymbol{v}_i - \boldsymbol{v}_j \right) \cdot \nabla W_{ij}(h_i),

となります。

状態方程式

ここまでで密度の計算式、運動方程式、エネルギー方程式の3式が導出できました。しかしながら、これらの式だけでは式が閉じないので、圧力の計算式として状態方程式を加えます。理想気体を仮定すると、状態方程式は比熱比 $\gamma$ を使って
$$
p = (\gamma - 1) \rho u,
$$
書き表せます。高校物理などでよく見る $pV = nRT$ とは違う形ですが、ごちゃごちゃ変形していくと同じ形になります。

人工粘性 (Artificial Viscosity)

これで流体の方程式が一通り離散化できましたが、実はこれだけでは衝撃波がうまく計算できません。衝撃波は分子の平均自由行程のスケールで起こる現象で、Euler方程式を普通に解くだけでは出てこない物理現象だからです。
試しに衝撃波管問題と呼ばれる問題をこれまでに導出した式を使って解いてみます。衝撃波管問題は厳密解を求めることができるため、圧縮性流体コードのテスト問題として非常によく使われます。
流体は1次元として、$t = 0$ での物理量を次のように設定します (Hernquist & Katz 1989)。

(v, \rho, p) =
\begin{cases}
(0, 1, 1) & x \leq 0.5\\
(0, 0.25, 0.1795) & x > 0.5
\end{cases},\\
\gamma = 1.4.

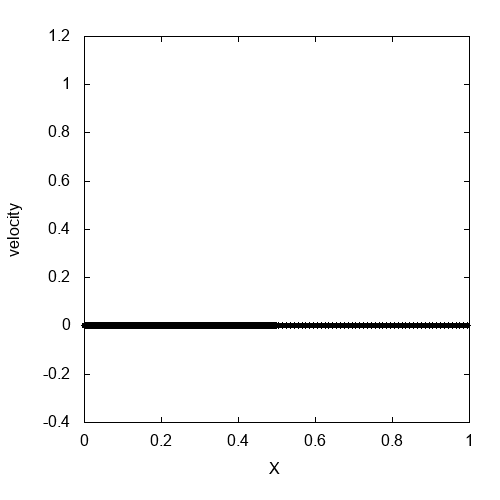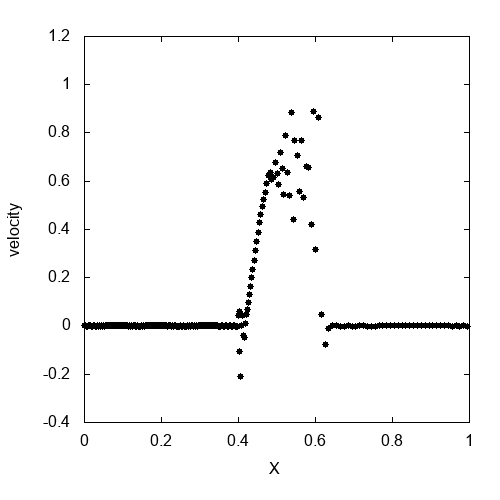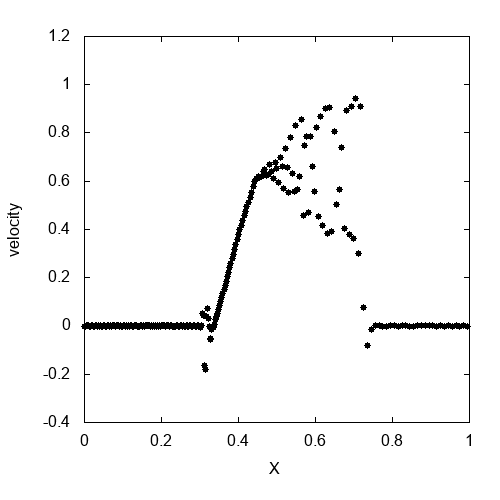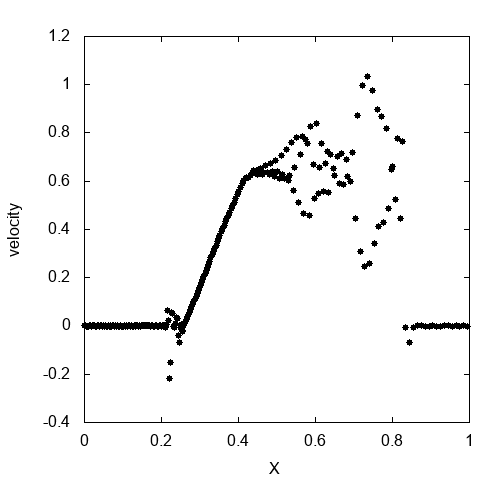
av0.gif
これが実際に計算して速度をプロットしたものです。速度が激しく振動しています。もちろん、解析解とは全く異なります。

SPH法で衝撃波を扱うには、衝撃波の発生箇所に人工粘性 (Artificial Viscosity)と呼ばれる人工的な散逸項を加える必要があります。人工粘性を入れることで、衝撃波面で速度分布が滑らかになり、数個の粒子で衝撃波を解像できるようになります。

人工粘性としてよく使われているのはMonaghan (1997)の人工粘性です。これは運動方程式とエネルギー方程式に以下の項を加えます。

\left( \frac{d \boldsymbol{v}_i}{dt} \right)_{\rm AV} = -\sum_j m_j \Pi_{ij} \nabla \bar{W}_{ij},\\
\left( \frac{d u_i}{dt} \right)_{\rm AV} = \frac{1}{2} \sum_j m_j \Pi_{ij} (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot \nabla \bar{W}_{ij},\\
\Pi_{ij} = \begin{cases}
-\alpha \frac{v_{ij}^{\rm sig} w_{ij}}{\rho_i + \rho_j} & (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot (\boldsymbol{r}_i - \boldsymbol{r}_j) < 0\\
0 & (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot (\boldsymbol{r}_i - \boldsymbol{r}_j) \geq 0
\end{cases},\\
v_{ij}^{\rm sig} = c_i + c_j - 3 w_{ij},\\
w_{ij} = (\boldsymbol{v}_i - \boldsymbol{v}_j) \cdot \frac{\boldsymbol{r}_i - \boldsymbol{r}_j}{|\boldsymbol{r}_i - \boldsymbol{r}_j|},\\
\bar{W}_{ij} = \frac{1}{2} \left[ W_{ij}(h_i) + W_{ij}(h_j) \right].

ここで、$c$ は音速を表します。$\alpha$ は人工粘性の強さを表す無次元量で、通常は1程度の値を使います。
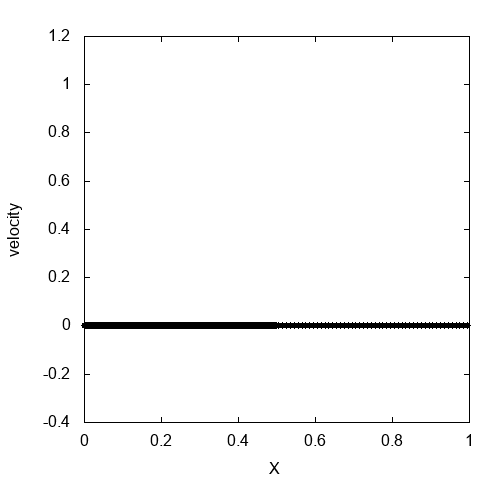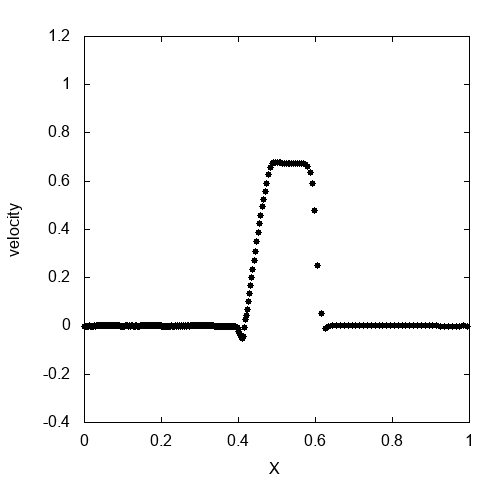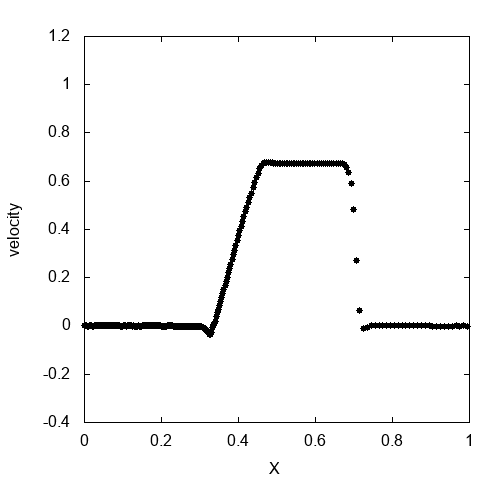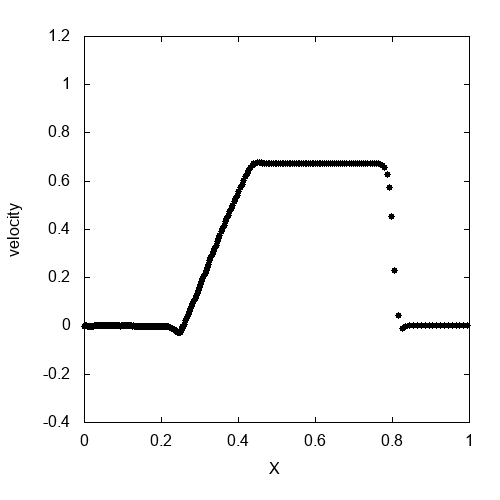
av1.gif
人工粘性を入れて先程の衝撃波管問題を解いたのが上のgifアニメです。人工粘性によって、衝撃波の後ろで発生していた数値振動を抑制することができました。
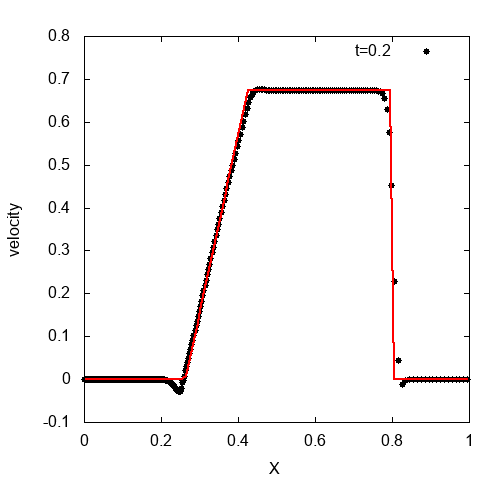
vel.gif
厳密解と比較したのが上の図です。厳密解に近い値がちゃんと得られていることが確認できます。

Balsara switch

式を見てわかる通り、SPH法の人工粘性は粒子同士が接近しているときに働くようになっています。従って、本来人工粘性が効いてほしい衝撃波領域の他に、シアー領域でも粘性が働いてしまいます。
シアー領域で発生する不要な人工粘性を取り除く手法として、人工粘性の式の $\Pi_{ij}$ を

\Pi_{ij} \rightarrow \frac{1}{2} ( F_i^{\rm b} + F_j^{\rm b} ) \Pi_{ij},\\
F_i^{\rm b} = \frac{ |\nabla \cdot \boldsymbol{v}_i| }{ |\nabla \cdot \boldsymbol{v}_i| + |\nabla \times \boldsymbol{v}_i| + \epsilon_{\rm b} c_i / h_i},\\
\epsilon_{\rm b} = 10^{-4},

で置き換える手法があります。これは Balsara switch (Balsara 1995)と呼ばれる方法で、速度の発散が小さい、つまり密度の時間変化が小さい領域で人工粘性を抑えることができます。

時間依存人工粘性

人工粘性をコントロールする方法として、速度場に応じて人工粘性係数 $\alpha$ を時間変化させる方法もあります。 Rosswog et al. (2000) では、粒子 $i$ の人工粘性係数を

\frac{d \alpha_i}{dt} = - \frac{\alpha_i - \alpha_{\rm min}}{\tau_i} + \max(-\nabla \cdot \boldsymbol{v}_i, 0) ( \alpha_{\rm max} - \alpha_i),

という式を使って計算しています。第1項は圧縮がなければ $\tau_i$ のタイムスケールで人工粘性係数が $\alpha_{\rm min}$ に減衰していくことを、第2項は圧縮領域で $\alpha_{\rm max}$ を上限に人工粘性係数を増やすことを表しています。式の中のパラメータは、Rosswog et al. (2000)では

\alpha_{\rm max} = 1.5,\\
\alpha_{\rm min} = 0.05,\\
\tau_i = \frac{h_i}{\epsilon_{\rm r} c_i},\\
\epsilon_{\rm r} = 0.2,

が使われています。

最後に

ここまでで導出した式を適当な時間積分法 (例えば、Runge-Kutta法、leap-frog法)を使って積分すると、圧縮性流体の運動を実際に計算できます。
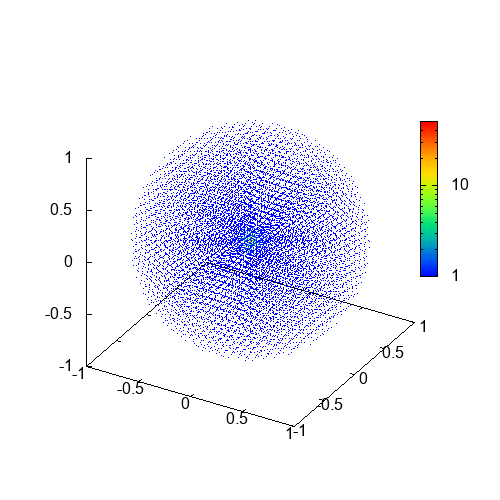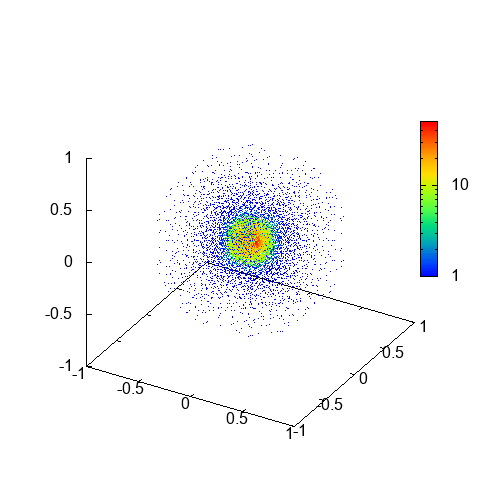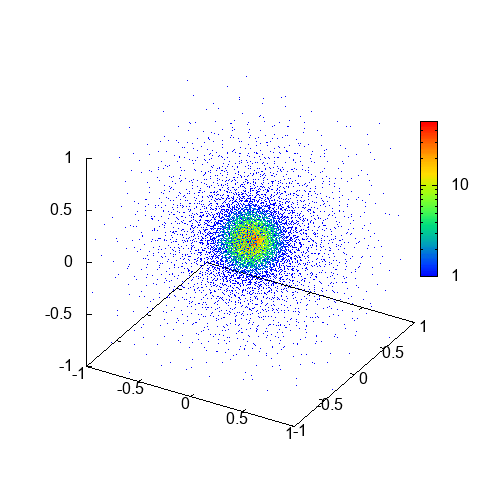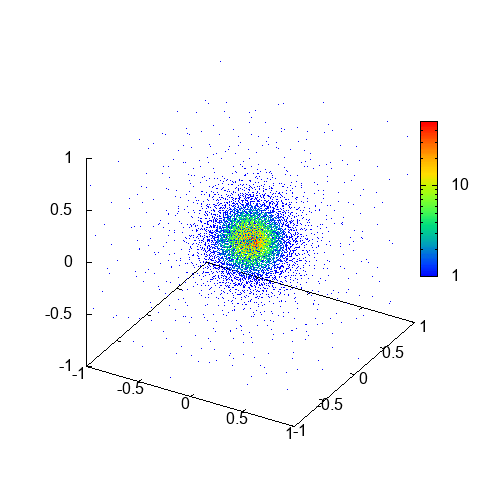
evrard_di.gif
上のgifアニメは、導出したSPH法の方程式に自己重力を加えて計算した結果です。色は密度を表しています。これはEvrard collapse (Evrard 1988)と呼ばれる問題で、ガス球が重力によって収縮した後、圧力勾配力と重力が釣り合った定常状態に落ち着くという物理過程が計算によって再現されています。
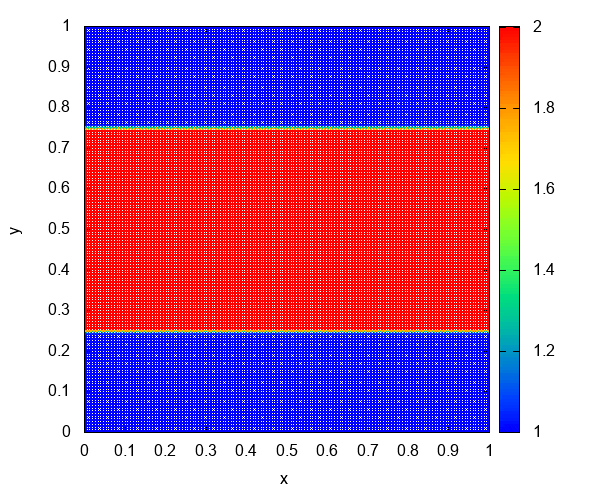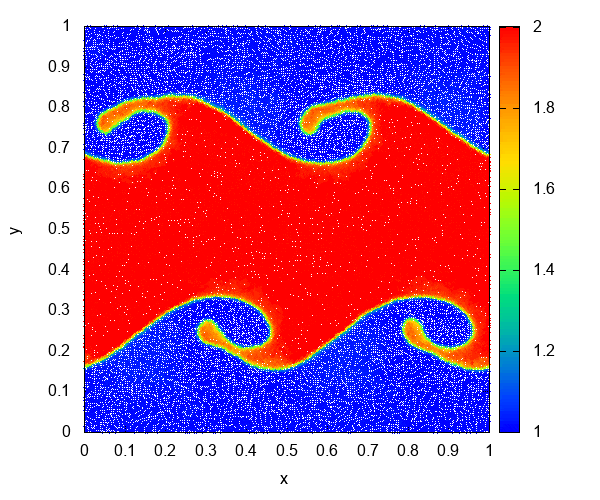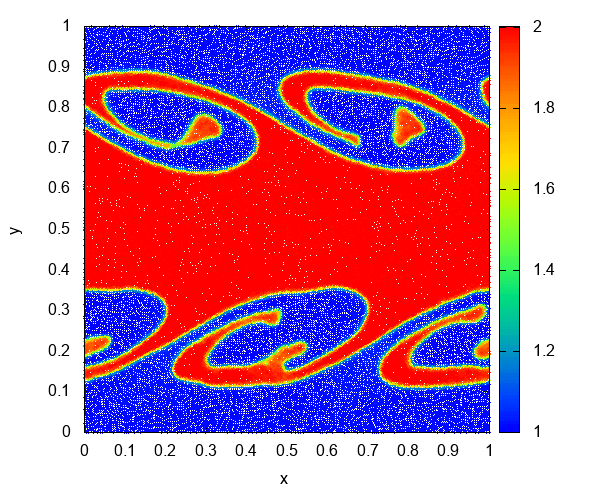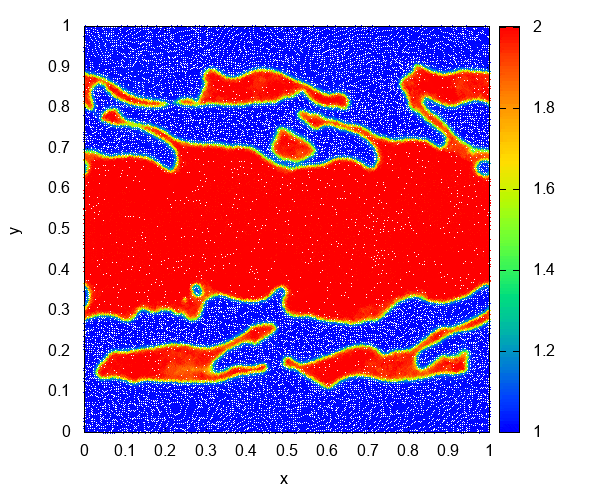
khi_st.gif
これはKelvin-Helmholtz不安定性のシミュレーションです。高密度領域と低密度領域に速度差があるとき、領域が接する面に存在していた摂動が渦を巻いて成長します。初期条件はSpringel (2010)を使っています。
Kelvin-Helmholtz不安定性をメッシュ法で計算すると Kelvin-Helmholtz instability - Discontinuous Galerkin hydrodynamics - YouTube のようになります。一方、SPH法の計算では、表面張力のような力が働いて、渦が分裂しています。

このように計算結果に違いが出てくるのは、SPH法が接触不連続面 (圧力が一定で密度が不連続)を正しく扱えないというところに原因があります (Agertz et al. 2007)。接触不連続面で非物理的な圧力勾配が発生し、それが表面張力のように作用してしまっています。この問題を解決する方法については理論編2で紹介します。

計算に使用したコードは https://github.com/mitchiinaga/sphcode に置いています。
ここで紹介した手法は全部実装しているので適当に遊んでみてください。

参考文献

47
36
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
47
36