ラビットチャレンジのレポートに関するリンクはこちら
ラビットチャレンジ 応用数学
ラビットチャレンジ 機械学習
ラビットチャレンジ 深層学習 Day1
ラビットチャレンジ 深層学習 Day2
ラビットチャレンジ 深層学習 Day3
ラビットチャレンジ 深層学習 Day4前半
ラビットチャレンジ 深層学習 Day4後半
1.勾配消失問題
・勾配消失問題とは、多層構造のネットワークを逆伝搬でパラメータ更新するときに次第に勾配が小さくなり、学習が進まなくなることである。
→解決法として、活性化関数の選択、重みの初期値設定、バッチ正規化の3つのアプローチがある。
・活性化関数の選択
シグモイド関数に代わり、ReLU関数を使用する。
ReLU関数を微分したときの値は1か0となり、勾配消失問題の回避とスパース化の効果がある。
・重みの初期値設定
Xavier法もしくはHe法を用いる。
Xavier法:重みの要素を、前の層のノード数の平方根で除算した値
$$\frac{1}{\sqrt{n}}$$
He法:重みの要素を、前の層のノード数の平方根で除算した値に対し√2を掛け合わせた値
$$\sqrt{\frac{2}{n}}$$
・バッチ正規化
ミニバッチ内の値を平均0、分散1となるように正規化する。
この後の最適化手法の説明時にバッチ正則化の有無について実装した結果を記載する
<確認テスト>
(1) 連鎖律の原理を使い、dz/dxを求めよ。
$$
z=t^2
$$
$$
t=x+y
$$
解答:
$$
\frac{dz}{dx}=\frac{dz}{dt}\frac{dt}{dx}
$$
$$
\frac{dz}{dt} = 2t
$$
$$
\frac{dt}{dx}=1
$$
$$
\frac{dz}{dx}=2t∗1=2(x+y)
$$
(2) シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値として正しいものを選択肢から選べ。
$$σ(z) = \frac{1}{1+exp(-z)}$$
$$
\frac{dσ}{dz} = (1-σ(z)) * σ(z) = (1-0.5)*0.5=0.25
$$
解答:(2) 0.25
(3) 重みの初期値に0を設定するとどのような問題が発生するか。簡潔に説明せよ。
解答:最初から意味のないネットワークとなり、パラメータ更新を行っても0で固定されたままとなってしまう。
(4) 一般的に考えられるバッチ正規化の効果を2点あげよ
解答:
1.学習が安定する。
2.計算速度の向上が期待できる。
2.学習率最適化手法
・パラメータの修正量を決める学習率はハイパーパラメータであり、適切な値を設定することが必要である。
・学習率が大きいと最適解に近づかずに発散してしまい、学習率が小さいと最適解までたどり着かない、もしくは局所最適解にはまってしまう懸念がある。
・初期の学習率を設定する手法が4つ提唱されている。
Momentum:誤差をパラメータで微分したものと学習率の積を減算した後、
現在の重みに前回の重みを減算した値と慣性の積を加算する。
Adagrad:誤差をパラメータで微分したものと再定義した学習率の積を減算する。
RMSProp:誤差をパラメータで微分したものと再定義した学習率の積を減算する。
Adam:モメンタムとRMSPropを組み合わせたようなアルゴリズム。現在はこの方法が主流。


<確認テスト>
(1) モメンタム・AdaGrad・RMSPropの特徴をそれぞれ簡潔に説明せよ。
解答:
・モーメンタム
局所最適解にならず、大域的最適解になる。
谷間についてから最も低い位置(最適値)にいくまでの時間が早い。
・Adagrad
勾配の緩やかな斜面に対して、最適値に近づける
学習率が徐々に小さくなるので、鞍点問題を引き起こすことがあった。
・RMSProp
局所最適解にはならず、大域的最適解となる。
ハイパーパラメータの調整が必要な場合が少ない
3.過学習
・過学習とは、特定の訓練サンプルに特化して学習することで、テストデータでよい精度を得られない状態を指す。
・特定の重みが大きくなりすぎることで過学習が発生するため、重みをある程度の大きさ以下でコントロールする必要がある。
・過学習を抑制する手段として、正則化とドロップアウトがある。
・L1正則化
損失関数に次のL1ノルムを加えて誤差の最小化を行う。
$$
λ\sum_{i=1}^n|w_i|
$$
・L2正則化
損失関数に次のL2ノルムを加えて誤差の最小化を行う。
$$
\frac{λ}{2}\sum_{i=1}^n|w_i|^2
$$
・ドロップアウト
結合層のノードをランダムに削除すること。
<確認テスト>
(1) 下図について、L1正則化を表しているグラフはどちらか答えよ。
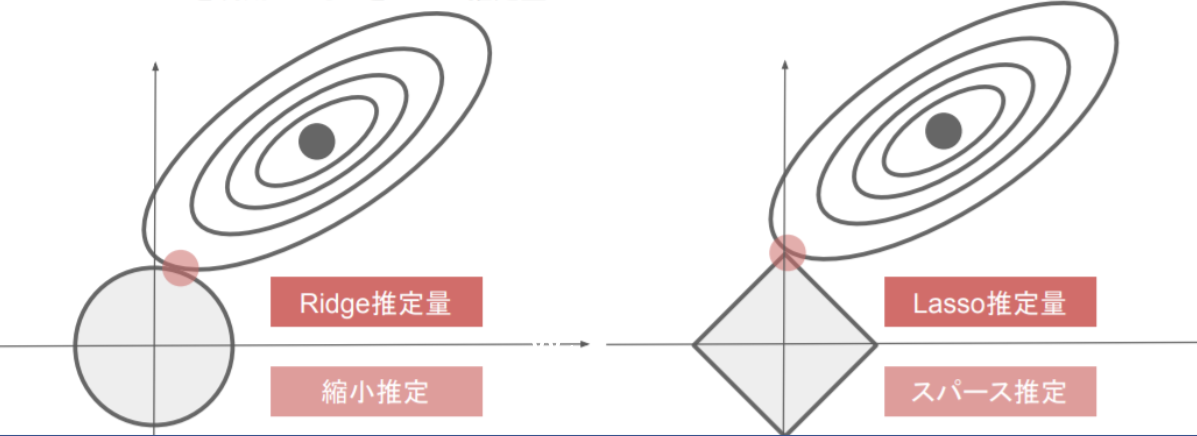
解答:右図
4.畳み込みニューラルネットワークの概念
・畳み込み層は、特徴として重要な情報を残す役割がある。
・畳み込み演算は、特定の重みが設定されたフィルターを用意し、入力画像からフィルターと同サイズの領域データ(部分行列)を切り出す。切り出した行列の左上から右下までの要素を順に掛け合わせていく。このフィルタをスライドさせて順番に計算させることで、圧縮した画像データが生成される。この計算過程で得られたデータは特徴マップと呼ばれる。

赤枠の領域に対して畳み込み演算をした場合
12 + 20 + 31 + 04 + 31 + 22 + 31 + 22 + 4*0 = 19
・畳み込み演算の用語について
バイアス:畳み込み演算後に足し合わせる固定値
パディング:画像データの周囲に値を埋め込むこと
ストライド:フィルタをずらす量
チャンネル:フィルタの数
・プーリング層は、切り出した領域の代表値(最大、最小、平均など)を取得する。
Max Poolingであれば下図の通り出力される。
<確認テスト>
(1) サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なおストライドとパディングは1とする。
解答:出力サイズの高さ・幅を求める公式は次の通り。
(Fh:フィルタ高さ、Fw:フィルタ幅、H:入力画像高さ、W:入力画像幅、P:パディング、S:ストライド)
高さ:
$$
O_h=\frac{H+2P−F_h}{S}+1
$$
幅:
$$
O_w=\frac{W+2P−F_w}{S}+1
$$
よって
高さ:
$$\frac{6 + 2 -2}{1} + 1 = 7$$
幅:
$$\frac{6 + 2 -2}{1} + 1 = 7$$
-> 7×7サイズの画像が得られる
5.最新のCNN(2021年現在では最新ではない)
講義資料で紹介されたAlexNetを含め、代表的なCNNベースのモデルをまとめる。
AlexNet:5つの畳み込み層と3つの結合層で構成される。ドロップアウトも実装されている。画像認識の制度を競い合う国際コンテスト"ILSVRC"でサポートベクトルマシンに代わりディープラーニングで初めて勝利したモデル。従来のモデルに対し10%ものエラー率を低減させた。

VGG-16:13層の畳み込み層と3層の全結合層により構成される。畳み込み層とプーリング層を単純に何層も重ねただけであるにもかかわらず、高い予測精度を持つ。畳み込み層が16層であるものはVGG-19と呼ぶ。
GoogleNet:22層で構成されており、従来手法とは異なる手法をいくつか用いている。異なるサイズの畳み込み層を並列につないだInceptionモジュールや、ネットワークを中間で分岐させ分類を行い、そこからも損失のフィードバックを得るAuxiliary Lossが使われている。さらに、全結合層を重ねる代わりにGlobal Average Pooling(GAP)を導入している。
ResNet:shortcut connectionを用いた残差ブロックを導入し勾配消失問題に対処することで、152層まで層を増やすことに成功した。shortcut connectionは畳み込み層を重ねたものをまたぐように、入力値をそのまま伝える。







