LoginSignup
28
20

More than 3 years have passed since last update.

@masatomix(Masatomi KINO)in株式会社プライム・ブレインズ

機械学習にでてくる勾配降下法/勾配ベクトルなどの整理。ついでにPythonで試してみた。

Last updated at Posted at 2019-05-01

さてさて ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 を絶賛学習中。前回書いた記事では、MNISTの手書き文字をニューラルネットワークで分類する件をちょっと整理したのでした。

勾配ベクトルとか、勾配降下法とか、損失関数の最小値とか

そのつづきの 4.4.1節の 勾配法 で「損失関数の最小値」を求めるという節があります。損失関数ってのは「ニューラルネットワークから出力されたAIがだした回答」と「教師データ(正解)」の誤差を算出する多変数関数です。

そして、その損失関数が最小になるようパラメタ(重みとバイアス)を調整することを「ニューラルネットワークの学習」と呼んでいるようですね。

さて 損失関数$f$の最小値を求める方法として勾配降下法(gradient descent method) ってのが出てきます。勾配降下法ってのは、ある初期値ベクトル $\boldsymbol{x_{0}}$から始まって、下記の漸化式にしたがって$\boldsymbol{x_i}$ を決めて

\boldsymbol{x_{i+1}} = \boldsymbol{x_{i}} - \eta 
\left(
\begin{array}{c}
\frac{\partial f}{\partial x^{0}}\\
\frac{\partial f}{\partial x^{1}}\\
\vdots
\end{array}
\right) \Big|_{\boldsymbol{x}=\boldsymbol{x_{i}}}

損失関数 $f(\boldsymbol{x_i})$ の値を順次計算していく、みたいな方法です。

この、ある ${\boldsymbol{x}=\boldsymbol{x_{i}}}$ における

\left(
\begin{array}{c}
\frac{\partial f}{\partial x^{0}}\\
\frac{\partial f}{\partial x^{1}}\\
\vdots
\end{array}
\right) =: \nabla f

を「勾配ベクトル」と呼びます。で、勾配ベクトルに微小な$\eta$ (これを学習率という) をかけて引くという漸化式を繰り返すことで、すこしずつ$\nabla f$の逆方向に進んでいくことになります。そして、勾配ベクトルの性質「勾配ベクトルの逆方向にすこし進むと、関数 $f$ の値はすこしだけ小さくなる」という性質により、$f$ の最小値の場所に収束していく、というのが勾配降下法の仕組みみたいですね。

勾配ベクトルってなんだっけ、、、？

勾配ベクトル、、うーん、むかーし学生の頃ならった気もするなーとおもいつつ「勾配ベクトルの逆方向にすこし進むと、関数 $f$ の値がすこしだけ小さくなる」ってのはなんだかすっかり忘れてたので、、、うん復習することにしました。

さて必要な前提知識は、下記の多変数関数のTaylor展開(というか一次近似式):

f(x,y) = f(x_0,y_0) + \frac{\partial \ f(x_0,y_0)}{\partial x}(x-x_0)+ \frac{\partial \ f(x_0,y_0)}{\partial y}(y-y_0)+ R(x,y)

(これは $\boldsymbol{x}$ が二次元の例で、$R$ は二次以上の無限小)。これと、ベクトルの内積の性質について:

\begin{align}
\|\boldsymbol{a}\|\|\boldsymbol{b}\| &\geq 
\boldsymbol{a}\cdot\boldsymbol{b} &(等号は、\boldsymbol{a} \ //\ \boldsymbol{b} のときのみ成立)\\
&= \sum_{i=1}^{n} a_ib_i \\
\end{align}

(よーするにCauchy–Schwarzの不等式) を用います。

先の多変数関数を一次近似した式は、下記のように式変形できます。$x-x_0 =:\Delta x,\ y-y_0 =:\Delta y$ として、


\begin{align}
f(x_0+\Delta x,y_0+\Delta y) - f(x_0,y_0) &= \frac{\partial \ f(x_0,y_0)}{\partial x}\Delta x+ \frac{\partial \ f(x_0,y_0)}{\partial y}\Delta y &+ R(x,y) \\
&= \left(
\begin{array}{c}
\frac{\partial f}{\partial x}\\
\frac{\partial f}{\partial y}\\
\end{array}
\right) \cdot \left(
\begin{array}{c}
\Delta x\\
\Delta y\\
\end{array}
\right) &+ R(x,y) \\
&=  \nabla f(x_0,y_0) \cdot \left(
\begin{array}{c}
\Delta x\\
\Delta y\\
\end{array}
\right) &+ R(x,y) 
\end{align}

さきの Cauchy–Schwarzの不等式 を用いることで

\begin{align}
f(x_0+\Delta x,y_0+\Delta y) - f(x_0,y_0) &= \nabla f(x_0,y_0) \cdot \left(
\begin{array}{c}
\Delta x\\
\Delta y\\
\end{array}
\right) &+ R(x,y) \\
&\leq \|\nabla f(x_0,y_0)\| \|\boldsymbol{\Delta x} \| &+ R(x,y) 
\end{align}

が成立します。等号は $\boldsymbol{\Delta x}$ が $\boldsymbol{\nabla f(x_0,y_0)}$ のスカラ倍のときのみ成立するので、そのときに $f$ の変化量が最大であることが分かりました。

さて $\boldsymbol{\Delta x}$ が $\boldsymbol{\nabla f(x_0,y_0)}$ のスカラ倍つまり $\boldsymbol{\Delta x} := k \boldsymbol{\nabla f(x_0,y_0)}$ のとき

\begin{align}
f(x_0+\Delta x,y_0+\Delta y) - f(x_0,y_0) &= \nabla f(x_0,y_0) \cdot \left(
\begin{array}{c}
\Delta x\\
\Delta y\\
\end{array}
\right) &+ R(x,y) \\
&= k \nabla f(x_0,y_0) \cdot \nabla f(x_0,y_0) &+ R(x,y) \\
&= k\|\nabla f(x_0,y_0)\|^2 &+ R(x,y) 
\end{align}\\

したがって $\Delta x, \Delta y$ が限りなく小さければ、つまり$k$が十分に小さければ、$R(x,y)$を無視することで、

f(x_0+\Delta x,y_0+\Delta y) - f(x_0,y_0) \approx  k\|\nabla f(x_0,y_0)\|^2

となることがわかりました。これは、$\Delta x, \Delta y$ が $\nabla f(x_0,y_0)$ と正方向におなじ向き($k>0$)に進んだときに、$f$ の値の変化量は正となる ことを示しています。

逆に$\ \boldsymbol{\Delta x} := -\eta \boldsymbol{\nabla f(x_0,y_0)} \ \ \ \ (\eta > 0)$ として $\nabla f(x_0,y_0)$ と平行に逆方向に進めば、

\begin{align}
f(x_0+\Delta x,y_0+\Delta y) - f(x_0,y_0) &= \nabla f(x_0,y_0) \cdot \left(
\begin{array}{c}
\Delta x\\
\Delta y\\
\end{array}
\right) &+ R(x,y) \\
&= -\eta  \nabla f(x_0,y_0) \cdot \nabla f(x_0,y_0) &+ R(x,y) \\
&= -\eta \|\nabla f(x_0,y_0)\|^2 &+ R(x,y) 
\end{align}\\

となり、$f$ の値を小さくする方向に進むということがわかります。したがって、ちびちびと $\eta$倍 づつ勾配ベクトルの逆方向に進んでいくことで、局所的には徐々に値が小さい方に行きそうだということが分かりました。

参考:

Pythonで計算してみる。

さて実際に

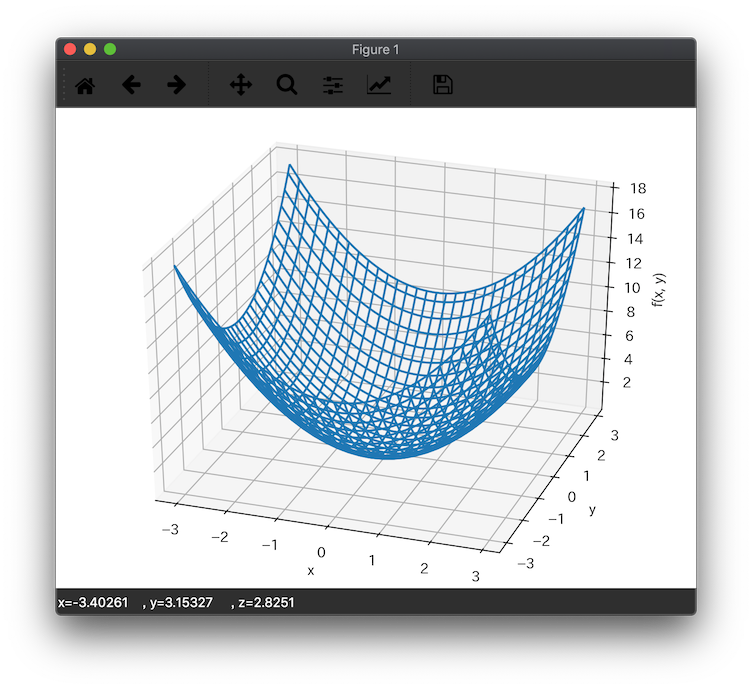
f(x,y) := x^2 + y^2

の最小値を勾配降下法で求めてみます。ちなみに$f$ はこんな感じの関数です。

image.png

式からも見た目からも、、原点(0,0)が最小値っぽいですが、、、。

数値微分と勾配降下法のコードは、MITライセンスで公開してくださっている
https://github.com/oreilly-japan/deep-learning-from-scratch/tree/master/ch04
を参考(ほぼ流用)にさせてもらいました。感謝です！

Pythonの分離環境作成

$ sw_vers
ProductName:    Mac OS X
ProductVersion: 10.14.4
BuildVersion:   18E226
$

$ python --version
Python 3.7.1

$ python -m venv ./venv
$ source ./venv/bin/activate
(venv) $

(venv) $ pip install numpy
(venv) $

やってみる

index.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
import sys

def main(args):
    lr = 0.10  # 学習率 η
    step_num = 100  # 繰返し回数

    def f(x):
        return x[0] ** 2 + x[1] ** 2

    init_x = np.array([-3.0, 4.0])  # 初期値は(x,y) = (-3,4)とした
    x1 = gradient_descent(f, init_x, lr=lr, step_num=step_num)

    print(x1)


def numerical_gradient(f, x):
    """
    ベクトル xと、多変数関数fを引数にとって、数値微分の結果をベクトルで返す
    :param f: 多変数関数
    :param x: ベクトル
    :return: 各成分で偏微分したベクトル。つまり勾配ベクトル
    """

    h = 1e-4
    grad = np.zeros_like(x)  # おなじかたちのゼロベクトル作成

    for index in range(x.size):  # ベクトルの各成分で偏微分
        tmp = x[index]  # 待避

        x[index] = tmp + h  # hすすめたf
        fx_plus_h = f(x)

        x[index] = tmp - h  # hもどしたf
        fx_minus_h = f(x)

        grad[index] = (fx_plus_h - fx_minus_h) / (2 * h)
        x[index] = tmp  # 待避してたxをもどす

    return grad


def gradient_descent(f, init_x, lr=0.01, step_num=100):
    """
    勾配降下法を用いて、fの最小値をとるベクトルxを計算して返す
    :param f: 対象の多変数関数
    :param init_x: 初期値ベクトル
    :param lr:  学習率
    :param step_num: 何回繰り返すか
    :return: 最小値となるベクトルx
    """
    x = init_x

    for index in range(step_num):
        grad = numerical_gradient(f, x)
        x = x - lr * grad

    return x


if __name__ == "__main__":
    main(sys.argv)

実行します。

(venv) $ python index.py 
[-6.11110793e-10  8.14814391e-10]

(venv) $

やっぱり、ほぼ原点の場所が最小値だって事が分かりました。

コードをすこしだけみてみると、まず、numerical_gradient関数は、関数とベクトルを引数にとって、その地点の勾配ベクトルを返しています。
gradient_descent 関数が勾配降下法を使って最小値の地点を求める関数です。init_xは初期値のベクトル、lrはいわゆる$\eta$(学習率)、step_numは、漸化式の繰返し回数です。

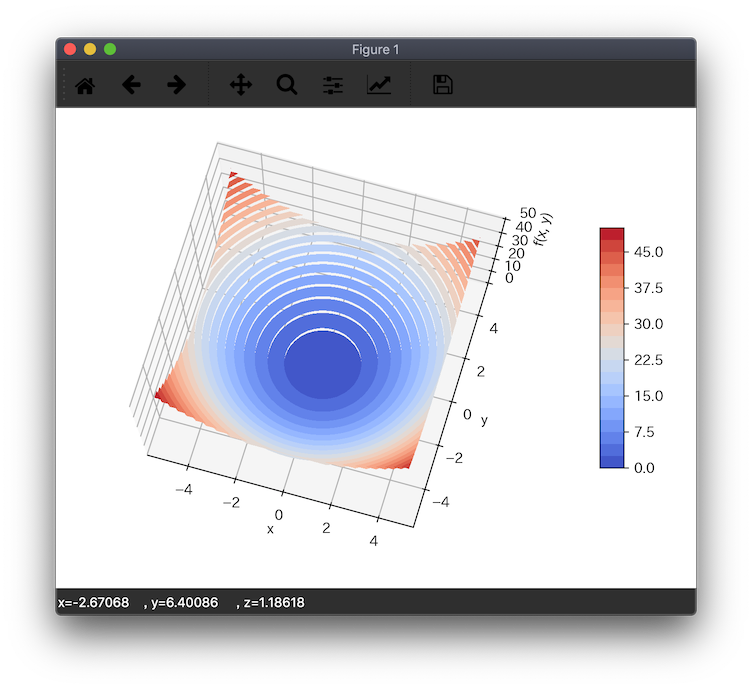
ちなみに、先のグラフを等高線付きで見てみると、

image.png

となってるので、図的にもあってそうですね。

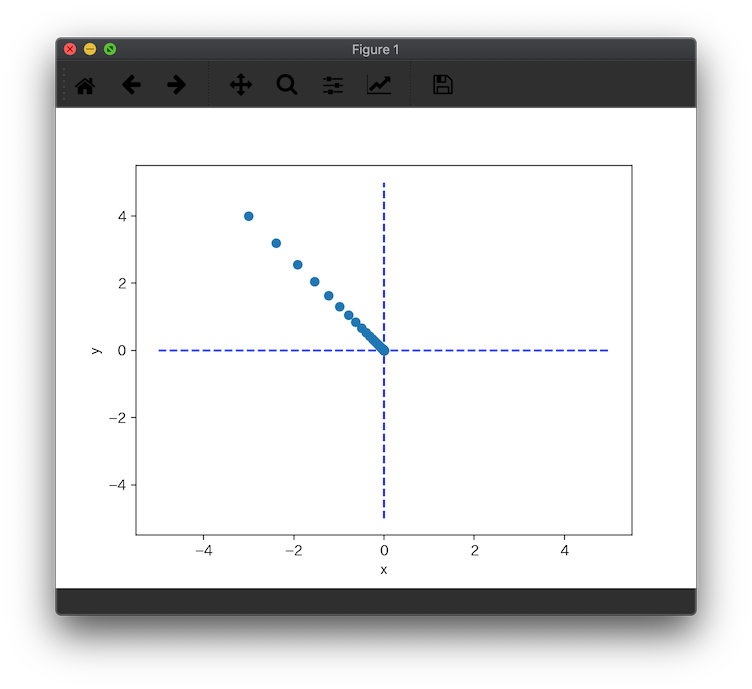
さて勾配降下法で、初期ベクトル$(x_0,y_0)= (-3,4)$ から始まって、原点までたどり着いたようですが、一応その軌跡を確認しておきます。といってもこれも書籍のコードとほぼ同様です。。

index_his.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
import sys
import matplotlib.pyplot as plt


def main(args):
    lr = 0.10  # 学習率 η
    step_num = 100  # 繰返し回数

    def f(x):
        return x[0] ** 2 + x[1] ** 2

    init_x = np.array([-3.0, 4.0])  # 初期値は(x,y) = (-3,4)とした
    x1, x_history = gradient_descent(f, init_x, lr=lr, step_num=step_num)

    print(x1)
    # print(x_history)

    plt.plot([-5, 5], [0, 0], '--b')  # 軸の描写
    plt.plot([0, 0], [-5, 5], '--b')  # 軸の描写
    plt.plot(x_history[:, 0], x_history[:, 1], 'o')

    plt.xlabel("x")
    plt.ylabel("y")
    plt.show()


def numerical_gradient(f, x):
    """
    ベクトル xと、多変数関数fを引数にとって、数値微分の結果をベクトルで返す
    :param f: 多変数関数
    :param x: ベクトル
    :return: 各成分で偏微分したベクトル。つまり勾配ベクトル
    """

    h = 1e-4
    grad = np.zeros_like(x)  # おなじかたちのゼロベクトル作成

    for index in range(x.size):  # ベクトルの各成分で偏微分
        tmp = x[index]  # 待避

        x[index] = tmp + h  # hすすめたf
        fx_plus_h = f(x)

        x[index] = tmp - h  # hもどしたf
        fx_minus_h = f(x)

        grad[index] = (fx_plus_h - fx_minus_h) / (2 * h)
        x[index] = tmp  # 待避してたxをもどす

    return grad


def gradient_descent(f, init_x, lr=0.01, step_num=100):
    """
    勾配降下法を用いて、fの最小値をとるベクトルxを計算して返す
    :param f: 対象の多変数関数
    :param init_x: 初期値ベクトル
    :param lr:  学習率
    :param step_num: 何回繰り返すか
    :return: 最小値となるベクトルx
    """
    x = init_x
    x_history = []

    for index in range(step_num):
        x_history.append(x.copy())
        grad = numerical_gradient(f, x)
        x = x - lr * grad

    return x, np.array(x_history)


if __name__ == "__main__":
    main(sys.argv)

実行します

(venv) $ python index_his.py 
[-6.11110793e-10  8.14814391e-10]
(venv) $

image.png

初期値$(-3,4)$から原点に向かって、勾配降下している事が確認出来ましたね！

おつかれさまでした。

(補足) 等高線付きグラフを出力するコード

蛇足ですが、さきほどの等高線付きグラフを出力するコードはこんな感じです。

(venv) $ pip install matplotlib
(venv) $ pip install PyQt5
3d.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-

import sys
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm


def func2(X, Y):
    return X ** 2 + Y ** 2


def main(args):
    x = np.arange(-5, 5, 0.25)
    y = np.arange(-5, 5, 0.25)

    X, Y = np.meshgrid(x, y)
    Z = func2(X, Y)

    fig = plt.figure()
    ax = Axes3D(fig)

    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_zlabel("f(x, y)")

    contour = ax.contourf(X, Y, Z, levels=20, cmap=cm.coolwarm)
    fig.colorbar(contour, shrink=0.5, aspect=10)
    plt.show()


if __name__ == "__main__":
    main(sys.argv)

参考:

おつかれさまでした。

関連リンク

28
20
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
28
20