微分をおさらいしつつ偏微分をつまみ食い！

• 機械学習に必要な高校数学やり直しアドベントカレンダー
  • 前の日 12/22(木) : ネイピア数 e の定義がなぜあの形か，先生は説明をしてくれなかった
  • 次の日 12/24(土) : クリスマスイヴでも「機械学習に必要な高校数学をやり直」す良い子たちへ，サンタからのクリスマスプレゼント

はじめに

こちらは「機械学習に必要な高校数学やり直しアドベントカレンダー」の 23 日目記事です。

昨日は yukisako さんの「ネイピア数 e の定義がなぜあの形か，先生は説明をしてくれなかった」でした。
ネイピア数 (Napier's constant) $e$ ･･･確かに高校数学の授業中に突然出てきて、「なんだこれは」ってなった記憶があります。
もしかしたら先生が由来も教えてくれていたかもしれませんが、もう覚えてないですね･･･ (ダメじゃん)。

ネイピア数の英語版 Wikipedia のページによれば、1683 年にヤコブ・ベルヌーイ (Jakob Bernoulli) が複利計算をしていた中で見つけた定数なのだそうです。
$e^x$ の導関数や原始関数が同じ (不定積分なら積分定数 $C$ はあるけれど) であることは、レオンハルト・オイラー (Leonhard Euler) による発見が大きいところです。
そういえば以前、こんなツイートをリツイートしたことがありました。

pic.twitter.com/FdxjS7Euee

— kenji (@kenjinote) 2016年11月23日

$e^x$ の特徴をうまく表した GIF だと思い、笑ってしまいながらも感心しました。

---

さて、私事ですが、今年は機械学習の基本について勉強する機会が多かったです。
そのうち、誤差逆伝播法についての勉強の記録をまとめた「誤差逆伝播法をはじめからていねいに」にはたくさんの「いいね」とストックをいただきまして、非常に嬉しく思っています。
この勢いのままに、今回アドベントカレンダーに初参加させていただくことにしました。

当初の予定では「二重数 (dual numbers)」を使った「自動微分 (automatic differentiation)」について書こうと思っていました。
しかしながら、二重数の微分の計算を試みているうちに偏微分が出てきてしまったため、それならば私が機械学習の前に勉強することになった、偏微分の基本的な考え方についてを書くほうがよいだろうと思い、急遽変更させていただきました。
「微分」に加えて ＋α の知識で取り組めるものであることと、たくさんのパラメータを扱う機械学習においては「偏微分」の知識が役に立つこともあり、高校数学から逸脱していることは承知のうえで取り扱ってみます。

なお、この記事は微分、偏微分のイメージを膨らませていただくことを目的としていますので、数学的に厳密な定義付けであったり、関数の連続性、微分・偏微分可能性などといった性質の言及については目をつぶっている部分があります。
そういった部分について深く知りたい場合は、教科書やそれに準じる各種資料等で補完していただければと思います。

途中の数式について

記事の前後から参照されている数式については右側に番号を振っています。
初回記載時は $\text{(1)}$ とかっこ付き数字で、2 回目以降記載時は $\text{[1]}$ と角かっこ付き数字で示します。記載済みの数式を変形したものについては $\text{(1')}$ とプライム付き数字で示します。

番号が振られていない数式は、前後から参照されなかったことを示すだけで、その式の重要性が低いことを表すものではありません。

微分は関数の「変化」を表すもの

「微分 (differentiation)」は、注目する関数の値がどう変化するか、その程度を求める演算であり、高校数学において大きなトピックの 1 つです。
ここでは微分の公式とか、そういったものは横に置いておいて、基本的な考え方についておさらいしてみます。

ある関数 $f(x)$ があって、変数 $x$ が $a$ から $b$ に移ったとき、$f(x)$ は増えるでしょうか、減るでしょうか。そしてどのくらい急な変化をするでしょうか。
この問いに対して、以下 $\text{(1)}$ のように、“$a$ と $b$ の差” に対する “$f(a)$ と $f(b)$ の差” の 比の値 を考えることができます。

\frac{f(b) - f(a)}{b - a} \tag{1}

これは幾何学的には、点 $(a, f(a))$ と点 $(b, f(b))$ を結ぶ 1 次関数の「傾き (slope)」を求めることと同義であり、$\text{(1)}$ の符号と絶対値によって、$f(x)$ がどう変化していくかが分かります。

ここで、$b$ を $a$ に近付けていくことを考えてみます。果たして $\text{(1)}$ の値はどうなるでしょうか。
以下の図 1 ～図 3 は、関数 $f(x) = \log x$ (緑の曲線) 上の 2 点 P、Q のうち、P を $(1, \log 1)$ に固定し、Q をそれぞれ $(5, \log 5)$、$(3, \log 3)$、$(1.5, \log 1.5)$ としたときの直線 PQ を図示しています。

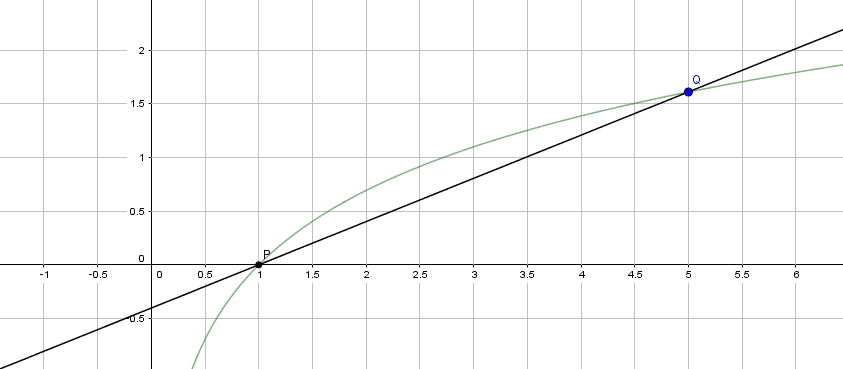
〈 図 1　$P(1, \log 1), Q(5, \log 5)$ 〉

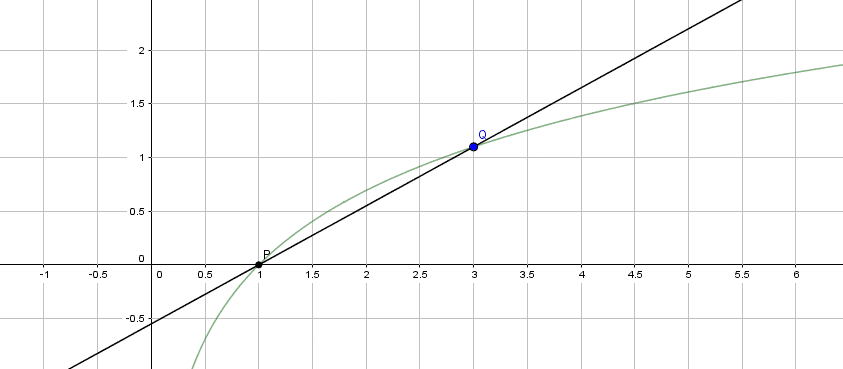
〈 図 2　$P(1, \log 1), Q(3, \log 3)$ 〉

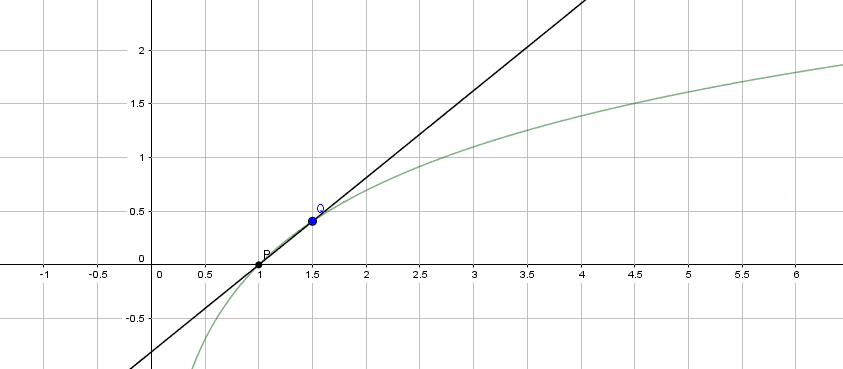
〈 図 3　$P(1, \log 1), Q(1.5, \log 1.5)$ 〉

図 1 で Q が $(5, \log 5)$ にいるとき、直線 PQ の傾きは比較的ゆるやかです。つまり $\text{(1)}$ の値も小さいわけです。
それに対して図 3 で Q が $(1.5, \log 1.5)$ にいるときは、直線 PQ の傾きはよりキツくなりました。これは $\text{(1)}$ の値が大きくなったことを意味します。

では、なぜ直線 PQ の傾きが大きくなったのでしょうか。それは P の付近では関数の値の変化が大きいからです。そしてそれが分かったのは P と Q を近くしたからだといえます。
2 点間の距離を小さくして $\text{(1)}$ の値を求めることで、局所的な関数の変化を観察することができるわけですね。

その “究極” として、この 2 点間距離を 限りなく 0 にする とどうなるかというと、$\text{(1)}$ の値は $f(x)$ のその点における 瞬間的な 変化率と見なすことができます。
この 限りなく 0 にする という行為を、数学記号 $\lim$ (「極限 (limit)」に由来します) を使い、

\lim_{b \to a} \frac{f(b) - f(a)}{b - a} = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} \quad \longleftarrow h = b - a \tag{2}

と表します。$\text{(2)}$ の場合、$x$ を $b$ から $a$ に近付けたわけですね。
2 点がぴったりとくっつき、$b = a$ (あるいは $h = b - a$ とおくと $h = 0$) になってしまうと 0 除算となり定義できませんが、限りなく近い 状態なら割っても問題ないという、ちょっぴり屁理屈っぽい式です。

これが $f(x)$ の $x = a$ における「微分係数 (differential coefficient)」であり、$x$ の定義域全体にわたって微分係数を求めること、あるいはもう少し意味を広げて、微分係数を求めるための式を立てることを「微分」といいます。
そして皆さんご存知のように、微分係数は幾何学的には $x = a$ における $f(x)$ のグラフの 接線の傾き を表しています。

ところで、$\text{(2)}$ は $x = a$ としたときの微分係数であり、微分係数も変数 $x$ によって決まる値であるといえます。そこで、

\frac{\mathrm{d}}{\mathrm{d}x} f(x) = f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} \tag{3}

と、変数 $x$ から微分係数を求める関数 (これを「導関数 (derivative)」といいます) として表すことができます。¹
$\dfrac{\mathrm{d}}{\mathrm{d}x} f(x)$ や $f'(x)$ は、$f(x)$ を微分したことを示す数学記号で、前者を「ライプニッツの記法 (Leibniz's notation)」、後者を「ラグランジュの記法 (Lagrange's notation)」とよびます。
微分を示す記号はほかにもありますが、一般にはこの 2 つがよく使われます。

微分は様々な用途に応用され、機械学習においても例外ではありません。
例えば、$f(x)$ が最小値をとるときの $x$ の値を「最急降下法 (gradient descent)」を使って求める場合、式 ² は

x^{(k+1)} = x^{(k)} - \eta \frac{\mathrm{d}}{\mathrm{d} x^{(k)}} f(x^{(k)}) \tag{4}

となり、$x$ の値を修正するための情報として、現在の $x^{(k)}$ に対する関数 $f$ の微分係数を必要とします。
微分係数の 符号 と 絶対値 を使って $x$ の修正方向と修正量をコントロールしているのです。
$f(x)$ が 2 次関数で下に凸なグラフを思い浮かべてみるとイメージしやすいのではないでしょうか。³

〈 図 4　2 次関数における最急降下法 〉

偏微分の考え方

変数を「固定」して減らす

ここまでご説明した「微分」は、関数の変数が 1 つしかない 1 変数関数 に対するものでした。
これと同じ考え方を 2 変数以上、つまり 多変数関数 に適用したいとしたら、どう考えればよいでしょうか･･･。⁴

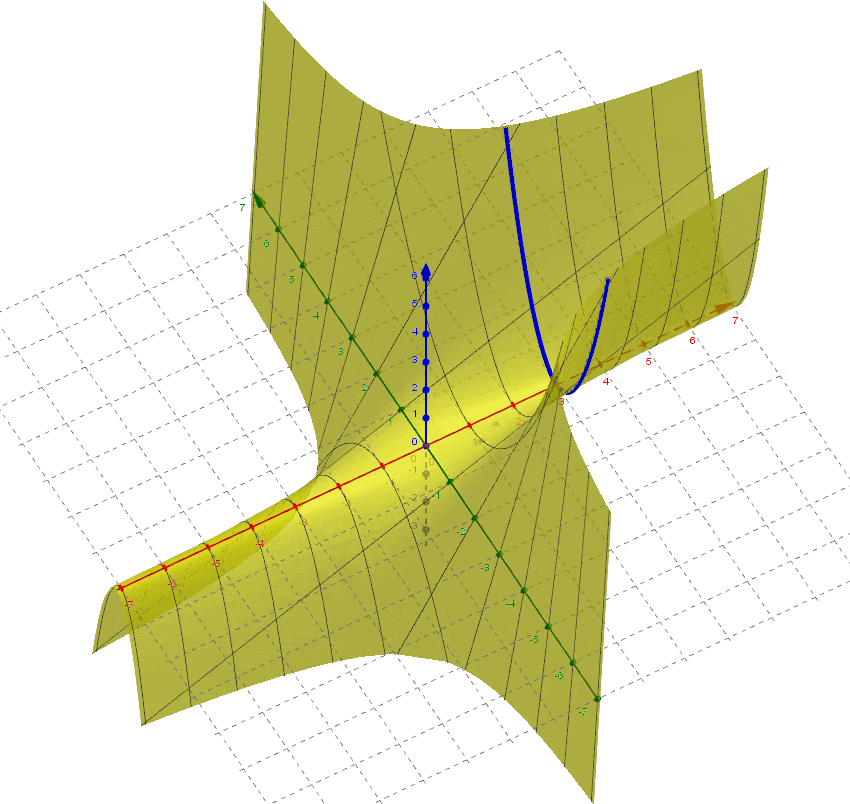
例として、2 変数関数 $f(x, y) = \dfrac{xy^2}{2}$ で考えてみましょう。この関数のグラフは以下、図 5 のように 3 次元空間に曲面として図示することができます。⁵

〈 図 5　$f(x, y) = \dfrac{xy^2}{2}$ 〉

早速この関数を微分したいところですが、いきなり 2 変数関数の微分をしろと言われても「さて、どうしたものか･･･」となってしまって先に進みません。
いま私たちが持っている知識は 1 変数関数の微分についてですから、まずは変数を 1 つだけにして考えてみましょう。
例えば $x$ だけ自由に動けるようにして、$y$ はどこかの値で固定します。
固定するということは、$y$ の部分は変数ではなく「定数 (constant)」として扱うことができるというわけです。

試しに $y = 1$ に固定して、$f(x, y)$ を計算してみると、

f(x, y)\Big|_{y = 1} = \frac{x}{2} \tag{5}

となります。とても簡単な 1 次関数ですが、しかし $f(x, y)$ の曲面上に確かに存在する直線です。

〈 図 6　$y = 1$ に固定すると $f(x, y)$ 上の点の集合は直線を形成する 〉

ここで $\text{(5)}$ を見てみると、$y = 1$ としたことで、関数の変数が $x$ だけになったわけですから、これを $g_1(x)$ とおいてみましょう。⁶
この状態なら微分ができますね！

\begin{align}
f(x, y)\Big|_{y = 1} = g_1(x) &= \frac{x}{2} \tag*{[5]} \\
g_1'(x) &= \frac{1}{2} \tag{6}
\end{align}

はい、いま、さらっと微分してしまいましたが、この微分にはどのような意味があるのか、出てきた $1/2$ という値の正体は何か、これらをきちんと理解しておく必要があります。

私たちは $f(x, y)$ の $y$ を 1 で固定することによって、$x$ だけを変数とする 1 変数関数を作り出しました。
そして、それを $x$ で微分したということは、作り出したその 1 変数関数の “瞬間の変化率” を求めたことにほかなりません。

この “瞬間の変化率” は、$y = 1$ にして $x$ だけを動かそうとしたときの $f(x, y)$ の変化率を示しています。
いま $\text{(6)}$ で出てきた $1/2$ という値は、$y = 1$ としたうえで $x$ を動かすとき、$f(x, y)$ の “瞬間の変化率” が $1/2$ ですよ、ということを意味しているのです。

そもそも関数 $f(x, y)$ が $x$ も $y$ も自由に動かせるはずなのに、$y = 1$ に固定して算出された変化率に何の意味があるの？と思う方もいらっしゃるかもしれません。
しかし、そこはもっとポジティブに考えてみましょう！
$y$ とかいう得体の知れないものに頼ることなく、我らが $x$ は単独で $f(x, y)$ に $1/2$ の影響を与えることができるんだぞ！と。
(影響が大きいか小さいかは別として･･･)

ちょっと大げさな物言いでしたが、ここで今までやってきたことを振り返ってみましょう。

私たちは $f(x, y)$ の $y$ を 1 に固定して、もはや 1 変数関数と化した $f$ を ($g_1$ とおき直しつつ) $x$ で微分したのでした。
つまりは $\text{(3)}$ に照らし合わせて以下の $\text{(7)}$ を計算したのです。

\begin{align}
\lim_{\Delta x \to 0} \frac{g_1(x + \Delta x) - g_1(x)}{\Delta x} &= \lim_{\Delta x \to 0} \frac{f(x + \Delta x, 1) - f(x, 1)}{\Delta x} \\
&= \lim_{\Delta x \to 0} \frac{ \dfrac{(x + \Delta x) \cdot 1^2}{2} - \dfrac{x \cdot 1^2}{2} }{\Delta x} \\
&= \lim_{\Delta x \to 0} \frac{ \ \dfrac{\Delta x}{2}\  }{\Delta x} \\
&= \frac{1}{2}
\end{align} \tag{7}

$\text{(3)}$ まで使っていた $h$ は、これ以降は $x$ 側の変化という意味で $\Delta x$ とおきます。$x$ 以外で $\Delta$ が出てきた場合も同様に読み替えてください。
ここで、$y$ を 1 ではなく元に戻して ⁷、その状態で $\text{(7)}$ を再計算してみると、

\begin{align}
\lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x} &= \lim_{\Delta x \to 0} \frac{ \dfrac{(x + \Delta x)y^2}{2} - \dfrac{xy^2}{2} }{\Delta x} \\
&= \lim_{\Delta x \to 0} \frac{ \ \dfrac{\Delta x \cdot y^2}{2}\  }{\Delta x} \\
&= \frac{y^2}{2}
\end{align} \tag{8}

となり、実は $y$ を固定して $x$ で微分した結果は、固定した $y$ の値に依存する、というオチでした。

変数の数だけ答えがある

今までは $y$ を固定し、$f(x, y)$ を $x$ のみを変数とする関数として考え、$x$ で微分しました。
勘付いている方もいらっしゃると思いますが、$x$ ではなく $y$ で同様の微分を考えることももちろん可能です。
今回は 2 変数関数ですが、それ以上の変数があっても同じことです。つまり、変数の数だけ微分を考えることができる わけですね。

例えば $x = 3$ に固定して、$f(x, y)$ を計算してみると、

f(x, y)\Big|_{x = 3} = \frac{3}{2} y^2 \tag{9}

となります。$y$ を固定したときとは異なり、今度は 2 次関数になりました。

〈 図 7　$x = 3$ に固定すると $f(x, y)$ 上の点の集合は放物線を形成する 〉

今度はこれを $g_2(y)$ とおき、$y$ で微分します。

f(x, y)\Big|_{x = 3} = g_2(y) = \frac{3}{2} y^2 \tag*{[9]}

\begin{align}
g_2'(y) = \lim_{\Delta y \to 0} \frac{g_2(y + \Delta y) - g_2(y)}{\Delta y} &= \lim_{\Delta y \to 0} \frac{f(3, y + \Delta y) - f(3, y)}{\Delta y} \\
&= \lim_{\Delta y \to 0} \frac{ \dfrac{3 (y + \Delta y)^2}{2} - \dfrac{3y^2}{2} }{\Delta y} \\
&= \lim_{\Delta y \to 0} \frac{ \ \dfrac{6y \Delta y + 3(\Delta y)^2}{2}\  }{\Delta y} = \lim_{\Delta y \to 0} \frac{6y + 3\Delta y}{2} \\
&= 3y
\end{align} \tag{10}

こちらでも同様に、$x$ を 3 ではなく元に戻して、その状態で $\text{(10)}$ を再計算してみると、

\begin{align}
\lim_{\Delta y \to 0} \frac{f(x, y + \Delta y) - f(x, y)}{\Delta y} &= \lim_{\Delta y \to 0} \frac{ \dfrac{x(y + \Delta y)^2}{2} - \dfrac{xy^2}{2} }{\Delta y} \\
&= \lim_{\Delta y \to 0} \frac{ \ \dfrac{2xy\Delta y + x(\Delta y)^2}{2}\  }{\Delta y} = \lim_{\Delta y \to 0} \frac{2xy + x\Delta y}{2} \\
&= xy
\end{align} \tag{11}

となります。⁸　$y$ を固定したときとは異なり、$x$ を固定したときは、$f(x, y)$ は変数 $y$ と固定した $x$ の値の両方に変化率が依存していることが分かります。

偏微分 ―― 1 変数の瞬間的な変化率

$f(x, y)$、そして $\text{(8)}$ と $\text{(11)}$ をもう一度確認しましょう。

\begin{align}
f(x, y) &= \frac{xy^2}{2} \\
\lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x} &= \frac{y^2}{2} \tag*{[8]} \\
\lim_{\Delta y \to 0} \frac{f(x, y + \Delta y) - f(x, y)}{\Delta y} &= xy \tag*{[11]}
\end{align}

$\text{(8)}$ は、$y$ を固定したときの、$f(x, y)$ の $x$ による “瞬間的な変化率” を表す式でした。
それに対して $\text{(11)}$ は、$x$ を固定したときの、$f(x, y)$ の $y$ によるそれを表す式でしたね。

皆さま大変お待たせいたしました。今回の主役の登場 ―― 実はこれらの、変数を 1 つにしぼったときの微分 のことを「偏微分 (partial differentiation)」といいます！

偏微分に関する名称をおさえておくと、微分における「導関数」は、偏微分では「偏導関数 (partial derivative)」といいます。
$\text{(8)}$ は $f(x, y)$ を $x$ について偏微分したときの「偏導関数」であり、同様に $\text{(11)}$ は $f(x, y)$ を $y$ について偏微分したときの「偏導関数」です。

そして、微分における「微分係数」は、偏微分では「偏微分係数 (partial differential coefficient)」といいます。
$\text{(6)}$、$\text{(7)}$ で求めた $1/2$ や、$\text{(10)}$ で求めた $3y$ がそれです。

偏微分を表す記号は $\partial$ (「ラウンド・ディー」とよぶことが一般的だと思います) であり ⁹、$f(x, y)$ を $x$ と $y$ それぞれで偏微分することは、

\begin{align}
\frac{\partial}{\partial x} f(x, y) &= \lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x} \tag{8'} \\
\frac{\partial}{\partial y} f(x, y) &= \lim_{\Delta y \to 0} \frac{f(x, y + \Delta y) - f(x, y)}{\Delta y} \tag{11'}
\end{align}

と表します。もっと一般的な書き方をすると、$f(x_1, x_2, \dots, x_k, \dots)$ の $x_k$ における偏微分は、

\frac{\partial}{\partial x_k} f(x_1, x_2, \dots, x_k, \dots) = \lim_{\Delta x_k \to 0} \frac{f(x_1, x_2, \dots, x_k + \Delta x_k, \dots) - f(x_1, x_2, \dots, x_k, \dots)}{\Delta x_k} \tag{12}

となります。

偏微分に関する公式は特にここでは詳しく書きませんが、変数として残している部分だけを微分し、固定した変数については (定数として扱うので) そのままにしておけば OK です。
あやしい場合は $\text{(8)}$ や $\text{(11)}$、$\text{(12)}$ に代入して計算をすれば確認ができますし、私たちは今までの中で $\dfrac{xy^2}{2}$ の偏微分を実際に計算しています。

最急降下法の理解

$\text{(4)}$ で「最急降下法」の 1 変数関数バージョンを書きましたが、一般にはベクトルを使って以下の式で表します。
(太字の $\boldsymbol{x}$ がベクトルであることを表しています)

\begin{align}
\boldsymbol{x}^{(k+1)} &= \boldsymbol{x}^{(k)} - \eta \frac{\partial}{\partial \boldsymbol{x}^{(k)}} f(\boldsymbol{x}^{(k)}) \\
&= \boldsymbol{x}^{(k)} - \eta \begin{bmatrix}
\dfrac{\partial f(\boldsymbol{x}^{(k)})}{\partial x_1^{(k)}} \\
\dfrac{\partial f(\boldsymbol{x}^{(k)})}{\partial x_2^{(k)}} \\
\vdots \\
\dfrac{\partial f(\boldsymbol{x}^{(k)})}{\partial x_n^{(k)}}
\end{bmatrix}
\end{align} \tag{13}

え!?　ベクトルの偏微分なんて今まで出てこなかったじゃないか！とお思いの方。ご安心ください。
高尚なことをしているわけではなく、単に複数の値の組をまとめて見やすくしているだけです。ホントです。

\begin{align}
x_1^{(k+1)} &= x_1^{(k)} - \eta \frac{\partial}{\partial x_1^{(k)}} f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) \\
&= x_1^{(k)} - \eta \cdot \lim_{\Delta x_1^{(k)} \to 0} \frac{ f(x_1^{(k)} + \Delta x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) - f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) }{\Delta x_1^{(k)}} \\
\\
x_2^{(k+1)} &= x_2^{(k)} - \eta \frac{\partial}{\partial x_2^{(k)}} f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) \\
&= x_2^{(k)} - \eta \cdot \lim_{\Delta x_2^{(k)} \to 0} \frac{ f(x_1^{(k)}, x_2^{(k)} + \Delta x_2^{(k)}, \dots, x_n^{(k)}) - f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) }{\Delta x_2^{(k)}} \\
\\
& \vdots \\
\\
x_n^{(k+1)} &= x_n^{(k)} - \eta \frac{\partial}{\partial x_n^{(k)}} f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) \\
&= x_n^{(k)} - \eta \cdot \lim_{\Delta x_n^{(k)} \to 0} \frac{ f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)} + \Delta x_n^{(k)}) - f(x_1^{(k)}, x_2^{(k)}, \dots, x_n^{(k)}) }{\Delta x_1^{(k)}} \\
\end{align} \tag{13'}

こんなものをいつも書きたくないのでｗ、ベクトル表記で省力化しているわけです。
しかしながら幸か不幸か？、$\text{(13')}$ によって、最急降下法のしくみが少し分かりやすくなったような気がします。
つまるところ、関数 $f$ には変数が山のようにある ¹⁰ けれども、偏微分を使うことで、その変数 だけで 関数 $f$ の値の増減にどれだけの影響を及ぼすかが分かります。
それを使って $x$ の値を修正するという点は、1 変数関数のときとまったく変わりません。

偏微分は関数と注目している変数 1 つに限定して変化率を考えることができるので、応用範囲が非常に広いです。
皆さんがこれから偏微分を使った式を見かけるようなことがあったら、この記事を思い出してくれると嬉しいです。

おわりに

偏微分と私

私は大学では情報工学科を履修していました。いわゆる “理系学科” ですから、当然数学に関するたくさんの科目がありましたし、特に微分積分学の講義は 必修 でした。
その過程で偏微分は当然習っているはずなのですが、その記憶はほとんどありません。お恥ずかしながら、真面目に履修していなかったのです。

しかしながら、時を経て、機械学習を勉強したいと思ったときに、偏微分の知識が必要になりました。
それまでの自分は、「偏微分？　$y$ を無視して $x$ だけ微分すればいいんでしょ？」という、暗記的な知識しかありませんでした。
それが “何を意味しているのか” をきちんと理解していませんでしたから、応用してもイメージが湧いてこなくて非常に困りました。

必要に迫られて偏微分の基礎を勉強し、そしてこうして Qiita の記事にまとめてみて、ようやく偏微分が意味しているものの根幹を吸収できたように思います。
それと同時に、勉強はやはり真面目にやっておかないといけない、ということを痛感するのでした。

数学を怖がらないで

アドベントカレンダーに参加されている方や、ご覧になっている方の中には、高校数学は途中から授業でやらなくなったから改めて勉強したいという方や、あるいはこれから勉強するという方もいらっしゃることと思います。
変な記号がいっぱい出てきたり、微分、複素数、ベクトル、行列、確率分布といった新しく習う概念が難しくて戸惑うこともあるでしょうけれども、ぜひとも過度に怖がらず、楽しく取り組んでいただければと思います。

きちんと勉強して理解し、自分の物にしておけば、案外それを使うことになる局面はおとずれるものです。
私は逆に微分はおろか線形代数学もまともに勉強してこなかったせいで、就職した業界が線形代数学をバリバリ使うところで四苦八苦したイヤな思い出があります。
ぜひとも私を反面教師にして踏み越えていってください！ｗ

最後までお読みいただきありがとうございました。
明日 12/24(土) は hidenori-t さんです。よろしくお願いします！
(私も予定がないので数学ではありませんがお勉強する予定でいますｗ)

奥付

記事には自分なりにしっかりと目を通してはいますが、誤字脱字、番号参照の間違い、表現の誤りなどがありましたら、コメント欄にてご指摘くださると幸いです。

• 初稿 「微分をおさらいしつつ偏微分をつまみ食い！」
  • 2016/12/23
• 第 2 稿 (タイトル変わらず)
  • 2016/12/24
  • 記事冒頭のアドベントカレンダー各記事へのナビゲーションのフォーマットを変更しました。
  • アドベントカレンダー 24 日目へのリンクを追加しました。
  • グラフの図を PNG から GIF へ変更し、減色してサイズを小さくしました。
  • 一部について加筆修正および図の追加を行いました。

1. 導関数も関数ですから、さらに微分して 高階な 導関数を考えることができます。 ↩

2. $x$ の右肩にあるかっこの中は累乗ではなく反復の回数を意味します。 ↩

3. 画像は A Neural Network in 13 lines of Python (Part 2 - Gradient Descent) より引用しました。 ↩

4. 2 変数以上に適用する微分としてこの記事ではこのあと「偏微分」をご説明していますが、もう 1 つ、「全微分 (total differentiation)」というものがあります。機械学習において「全微分」が必要になる局面はほとんどないと思いますが、しかしながら微分積分学において重要な概念です。 ↩

5. 以降の 3 次元空間のグラフは、赤色の軸は $x$ 軸、緑色の軸は $y$ 軸、青色の軸は $z$ 軸を意味します。 ↩

6. あとでもう 1 つ似たような関数が出てくるのですが、$g$ に対してそれを $h$ としてしまうと $\text{(2)}$ の $h$ とかぶってしまうため、泣く泣く番号で区別することにしました。 ↩

7. 元に戻しても $y$ は依然として 何らかの値で固定 されていて、変数に戻ったわけではありません。 ↩

8. $\text{(11)}$ で $\Delta y$ は (極限まで近付けるけれども) 0 ではないにもかかわらず、最後のイコール前後で $\Delta y$ を 0 として扱っているように見えますが、最終的に $xy$ になる ということを表していて、依然として $\Delta y$ は 0 ではありません。このような「無限小 (infinitesimal)」の考え方も、本来はきちんと理解しておく必要があるのですが、厳密性を求められない限り、割とざっくりでも何とかなります。 ↩

9. $\mathrm{d}$ は多変数関数においては「全微分」を表す記号として使われるため、「偏微分」には新しい記号 $\partial$ が使われています。1 変数関数では偏微分を考える必要がありませんので、微分では $\mathrm{d}$ を使います。 ↩

10. それこそ実用的なニューラルネットワークになると平気で「万」や「億」のオーダになることもあります。 ↩