お、Qiitaって数式つかえるんですね。。ってことで、数式をつかっていろいろ書いてみます。。
三角関数の定義
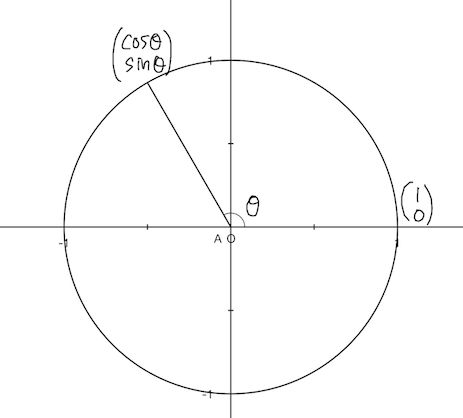
$\cos\theta ,\sin\theta $を以下のように定義します。
$x$軸正方向と角$\theta$ をなす 長さ1のベクトルを
\left(
\begin{array}{c}
\cos\theta\\
\sin\theta
\end{array}
\right)
とします。
ようするに、単位円 $ x^2 + y^2 = 1 $ 上のある点 $P$ が $x$軸正方向と角$\theta$ をなすとき、その$x$座標、$y$座標を
$\left(
\begin{array}{c}
\cos\theta,
\sin\theta
\end{array}
\right)
$ とするってことですね。
内積の定義
あるベクトル$\boldsymbol{a}$,$\boldsymbol{b}$ に対して、内積 $\boldsymbol{a}\cdot\boldsymbol{b}$ を以下のように定義します。
\boldsymbol{a}\cdot\boldsymbol{b} := \|\boldsymbol{a}\|\|\boldsymbol{b}\|\ \cos\theta
(ただし$\theta$は二つのベクトルのなす角)
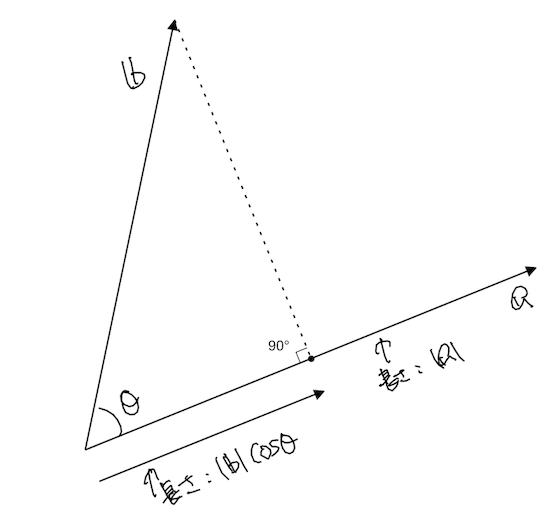
この図形的な意味って、
\begin{align}
\boldsymbol{a}\cdot\boldsymbol{b} &= \|\boldsymbol{a}\|\|\boldsymbol{b}\|\ \cos\theta\\
&=\|\boldsymbol{a}\|\times( \|\boldsymbol{b}\|\ \cos\theta)\\
\end{align}
とみると「ベクトル$\boldsymbol{a}$の長さ」と、「ベクトル$\boldsymbol{b}$をベクトル$\boldsymbol{a}$へ正射影したときの有向長」をかけたモノ、と考えることができます。
内積の分配法則
内積をこのように定義すると、内積には分配法則が成り立ちます。つまり、
\boldsymbol{a}\cdot(\boldsymbol{b}+\boldsymbol{c}) =
\boldsymbol{a}\cdot\boldsymbol{b}+\boldsymbol{a}\cdot\boldsymbol{c}
ということです。
なぜならば
$\boldsymbol{b} + \boldsymbol{c} =:\boldsymbol{d}$ とすると
\begin{align}
\boldsymbol{a}\cdot(\boldsymbol{b}+\boldsymbol{c}) &=\boldsymbol{a}\cdot\boldsymbol{d}\\
&=\|\boldsymbol{a}\|\times( \boldsymbol{d}を\boldsymbol{a}へ射影したときの長さ)\\
&=\|\boldsymbol{a}\|\times( \boldsymbol{b}を\boldsymbol{a}へ射影したときの長さ +\boldsymbol{c}を\boldsymbol{a}へ射影したときの長さ )\\
&=\|\boldsymbol{a}\|\times( \boldsymbol{b}を\boldsymbol{a}へ射影したときの長さ) +\|\boldsymbol{a}\|\times(\boldsymbol{c}を\boldsymbol{a}へ射影したときの長さ )\\
&=\boldsymbol{a}\cdot\boldsymbol{b}+\boldsymbol{a}\cdot\boldsymbol{c}\\
(Q.E.D.)
\end{align}
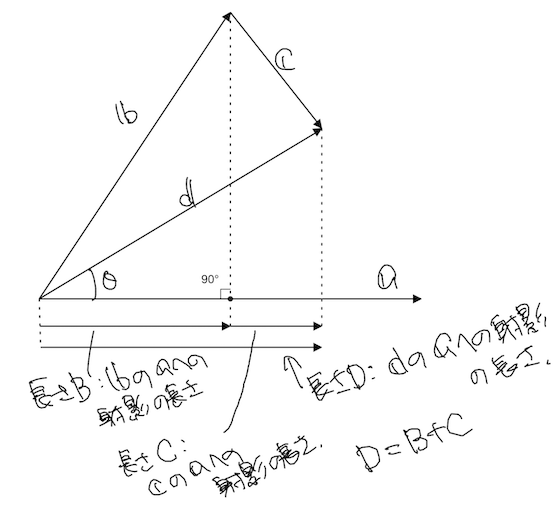
図で表すと、
こういうことですね。。
内積の成分表示の有名なヤツ。
分配法則をつかうと、2次元の場合を例にしますが
\boldsymbol{a} =
\left(
\begin{array}{c}
a_1\\
a_2
\end{array}
\right)
,
\boldsymbol{b} =
\left(
\begin{array}{c}
b_1\\
b_2
\end{array}
\right)
\boldsymbol{e_1} =
\left(
\begin{array}{c}
1\\
0
\end{array}
\right)
,
\boldsymbol{e_2} =
\left(
\begin{array}{c}
0\\
1
\end{array}
\right)
としたとき
\begin{align}
\boldsymbol{a}\cdot\boldsymbol{b} &=(a_1\boldsymbol{e_1}+a_2\boldsymbol{e_2})\cdot(b_1\boldsymbol{e_1} +b_2\boldsymbol{e_2})\\
&=a_1 b_1 \boldsymbol{e_1}\cdot\boldsymbol{e_1}+a_2b_2\boldsymbol{e_2}\cdot\boldsymbol{e_2}\\
&\qquad + a_1 b_2 \boldsymbol{e_1}\cdot\boldsymbol{e_2}+a_2 b_1 \boldsymbol{e_2}\cdot\boldsymbol{e_1}\\
&= a_1b_1 + a_2b_2\\
&=\|\boldsymbol{a}\|\|\boldsymbol{b}\|\ \cos\theta
\end{align}
が成立します。
(内積の$\cos\theta$をかけるという定義により、$\boldsymbol{e_1}\cdot\boldsymbol{e_1} =\boldsymbol{e_2}\cdot\boldsymbol{e_2} =1,\quad\boldsymbol{e_1}\cdot\boldsymbol{e_2} =\boldsymbol{e_2}\cdot\boldsymbol{e_1} =0$であるため)
コレ、基底ベクトルを $\boldsymbol{e_1}..\boldsymbol{e_n}$と $n$次元で考えた場合、各基底ベクトルの内積が、自分以外との内積は0,自分との内積は1であることに注意すると、$n$次元でも成立します。つまり、
$n$次元のベクトル $\boldsymbol{a} ,\boldsymbol{b}$
\boldsymbol{a} =
\left(
\begin{array}{c}
a_1\\
a_2\\
\vdots\\
a_n\\
\end{array}
\right)
,
\boldsymbol{b} =
\left(
\begin{array}{c}
b_1\\
b_2\\
\vdots\\
b_n\\
\end{array}
\right)
について、
\begin{align}
\boldsymbol{a}\cdot\boldsymbol{b} &=\|\boldsymbol{a}\|\|\boldsymbol{b}\|\ \cos\theta\\
&= a_1b_1 + a_2b_2 ... +a_nb_n\\
&= \sum_{i=1}^{n} a_ib_i
\end{align}
となります。
ベクトルから cos θを求める
$\boldsymbol{a}$,$\boldsymbol{b}$ 二つのベクトルのなす角を $\theta$としたとき、
\begin{align}
\cos\theta &= \frac{\boldsymbol{a}\cdot\boldsymbol{b}}{\|\boldsymbol{a}\|\|\boldsymbol{b}\|}\\
&= \frac{\sum_{i=1}^{n} a_ib_i}{\sqrt{\sum_{i=1}^{n} a_i^2} \cdot \sqrt{\sum_{i=1}^{n} b_i^2}}
\end{align}
これを計算することでなす角(の $\cos\theta$ )が求まるって事ですねー。。この $\cos\theta$ですが、統計ででてくるいわゆる相関係数です。
統計の話
相関係数
\boldsymbol{x} =
\left(
\begin{array}{c}
x_1 -m_x\\
x_2 -m_x\\
\vdots\\
x_n -m_x\\
\end{array}
\right)
,
\boldsymbol{y} =
\left(
\begin{array}{c}
y_1 -m_y\\
y_2 -m_y\\
\vdots\\
y_n -m_y\\
\end{array}
\right)
という$n$次元ベクトル$\boldsymbol{x},\boldsymbol{y}$ について、
\begin{align}
r_{xy} :&= \frac{\boldsymbol{x}\cdot\boldsymbol{y}}{\|\boldsymbol{x}\|\|\boldsymbol{y}\|}\\
&=\frac{\sum_{i=1}^{n} (x_i -m_x)(y_i -m_y)}{\sqrt{\sum_{i=1}^{n} (x_i -m_x)^2} \cdot \sqrt{\sum_{i=1}^{n} (y_i -m_y)^2}}\\
&= (\boldsymbol{x}と\boldsymbol{y}のなす角\theta の \cos\theta )
\end{align}
と定義します。ただし
m_x:= \frac{1}{n} \sum_{i=1}^{n}x_i \\
m_y:= \frac{1}{n} \sum_{i=1}^{n}y_i
つまり$m_x,m_y$ は、各成分の平均で定数値です。
この値$r_{xy} $は $\cos\theta$ なので $-1 \leq r_{xy} \leq 1$ の値をとり、0だと直交、1だと平行(向きも同じ)、-1だと平行(向きが逆) ってことになります。
$(x_1,y_1),(x_2,y_2), \dots (x_n,y_n)$ のデータの関係を見るときに、$\boldsymbol{x},\boldsymbol{y}$ ふたつのベクトルの $\cos\theta$ を測ることで相関をみるってことで、$r_{xy} $ を相関係数ってよんでます。
標準偏差と共分散
\begin{align}
r_{xy}
&=\frac{\sum_{i=1}^{n} (x_i -m_x)(y_i -m_y)}{\sqrt{\sum_{i=1}^{n} (x_i -m_x)^2} \cdot \sqrt{\sum_{i=1}^{n} (y_i -m_y)^2}}\\
&=\frac{\frac{1}{n}\sum_{i=1}^{n} (x_i -m_x)(y_i -m_y)}{\sqrt{\frac{1}{n}\sum_{i=1}^{n} (x_i -m_x)^2} \cdot \sqrt{\frac{1}{n}\sum_{i=1}^{n} (y_i -m_y)^2}}\\
&=\frac{S_{xy}}{S_xS_y}
\end{align}
ただし
\begin{align}
S_{xy}&:=\frac{1}{n}\sum_{i=1}^{n} (x_i -m_x)(y_i -m_y)\\
S_x&:=\sqrt{\frac{1}{n}\sum_{i=1}^{n} (x_i -m_x)^2}\\
S_y&:=\sqrt{\frac{1}{n}\sum_{i=1}^{n} (y_i -m_y)^2}
\end{align}
$S_x,S_y$は、一次元のときにもよく出てくる$\boldsymbol{x},\boldsymbol{y}$ の標準偏差、$S_{xy}$を$\boldsymbol{x}$と$\boldsymbol{y}$の共分散と呼びます。
相関係数を計算するときに、標準偏差と共分散を計算して算出しますが、これってつまるところ二つのベクトルのなす角を調べることで、データに相関があるかなーってのを $-1 \leq r_{xy} \leq 1$ で計算してるって事が分かります。
Pythonでやってみる
ついでに、これらの値をPythonのnumpyライブラリをつかって実際に計算してみます。。。
以下はとあるヒトの体重と体脂肪、BMIデータです。
実際のデータ:
$ head weight.csv
key,体重,体脂肪率,BMI
2017-12-10,58.5750,14.2425,23.4000
2017-12-11,58.6333,14.1255,23.4333
2017-12-12,58.3250,14.4700,23.3500
2017-12-13,58.4000,14.8275,23.3500
2017-12-14,57.2000,14.1450,22.9000
2017-12-15,57.9500,13.6900,23.2000
2017-12-16,58.0000,14.3400,23.2000
2017-12-17,58.6167,14.0995,23.4333
2017-12-18,58.7500,14.0150,23.4500
.....
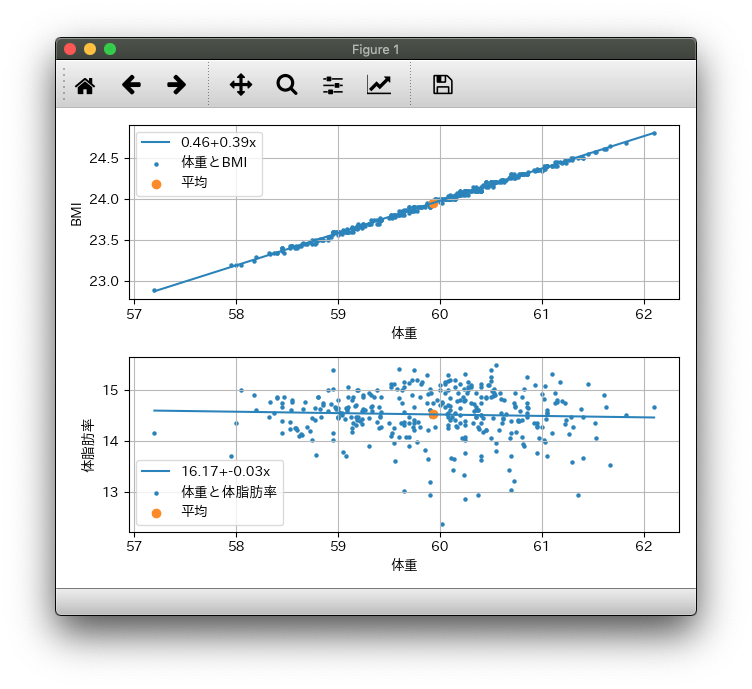
BMIは身長と体重から計算されるので、相関は極めて高いはずです(というかほぼ1になるはず?)。体脂肪は、どうでしょうか。。
環境
$ sw_vers
ProductName: Mac OS X
ProductVersion: 10.14.1 (Mojaveです)
BuildVersion: 18B75
Pythonの実行環境は適宜ご用意してもらえば結構ですが、以下、venvで環境を構築する手順を書いておきます。
$ python3 -m venv ./venv
$ source ./venv/bin/activate
(venv) $ which python3
/xxx/venv/bin/python3
(venv) $ python3 --version
Python 3.7.1
(venv) $
また、グラフを表示するために、Matplotlib を使用しますが、Macの環境構築に戸惑ったらこちらをご参照ください。
実行してみる
(venv) $ cat requirement.txt
matplotlib==3.0.2
numpy==1.15.4
pandas==0.23.4
PyQt5==5.11.3
(venv) $ pip install -r requirement.txt
... 割愛
(venv) $ cat weight.py
# !/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sys
def main(args):
# データ読み込み
df = pd.read_csv('./weight.csv', index_col='key')
print(df.head(10))
print(df.shape)
# データ列取り出し
data1 = df['体重']
data2 = df['体脂肪率']
data3 = df['BMI']
# 平均
mean1 = np.mean(data1) # mx
mean2 = np.mean(data2) # my
# 分散と、共分散
v1 = np.var(data1, ddof=0) # 1/n * Σ (X-mx)^2
v2 = np.var(data2, ddof=0) # 1/n * Σ (Y-my)^2
cov = np.cov(data1, data2, ddof=0)[1, 0] # 1/n * Σ (X-mx)*(Y-my)
# 共分散は共分散行列で返ってくるので、[1,0],[0,1] をとればいい
# 標準偏差
std_dev1 = np.sqrt(v1)
std_dev2 = np.sqrt(v2)
# 相関係数
cor = np.corrcoef(data1, data2)[1, 0]
cor2 = cov / (std_dev1 * std_dev2) # もしくは計算で。
print('--- 体重と体脂肪率 ----')
print(f' 平均: {mean1:.3f}, {mean2:.3f}')
print(f'標準偏差: {std_dev1:.3f}, {std_dev2:.3f}')
print(f' 分散: {v1:.3f}, {v2:.3f}')
print(f' 共分散: {cov:.10f}')
print(f'相関係数: {cor:.10f}')
print(f'相関係数: {cor2:.10f}')
print('-------')
# ちなみに体重とBMIの相関係数
cor3 = np.corrcoef(data1, data3)[1, 0]
print(f'体重とBMIの相関係数: {cor3:.10f}')
plot(df)
def plot(df):
xorg = df['体重']
yorg = df['BMI']
mx = np.mean(xorg)
my = np.mean(yorg)
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.scatter(xorg, yorg, label='体重とBMI', s=5)
ax1.scatter(mx, my, label='平均')
ax1.set_xlabel('体重')
ax1.set_ylabel('BMI')
ax1.grid(True) # グリッド線
plot_poly_1d(ax1, xorg, yorg)
ax1.legend(loc='upper left')
yorg2 = df['体脂肪率']
my2 = np.mean(yorg2)
ax2.scatter(xorg, yorg2, label='体重と体脂肪率', s=5)
ax2.scatter(mx, my2, label='平均')
ax2.set_xlabel('体重')
ax2.set_ylabel('体脂肪率')
ax2.grid(True) # グリッド線
plot_poly_1d(ax2, xorg, yorg2)
ax2.legend(loc='lower left')
plt.tight_layout() # タイトルの被りを防ぐ
# グラフに情報を表示
plt.show()
# 線形回帰直線
def plot_poly_1d(ax, xorg, yorg):
# y = ax + b のa ,b を配列で返す
poly_fit = np.polyfit(xorg, yorg, 1)
# 関数を作成
poly_1d = np.poly1d(poly_fit)
xs = np.linspace(xorg.min(), xorg.max())
ys = poly_1d(xs)
ax.plot(xs, ys, label=f'{poly_fit[1]:.2f}+{poly_fit[0]:.2f}x')
if __name__ == "__main__":
main(sys.argv)
(venv) $ python3 weight.py
体重 体脂肪率 BMI
key
2017-12-10 58.5750 14.2425 23.4000
2017-12-11 58.6333 14.1255 23.4333
2017-12-12 58.3250 14.4700 23.3500
2017-12-13 58.4000 14.8275 23.3500
2017-12-14 57.2000 14.1450 22.9000
2017-12-15 57.9500 13.6900 23.2000
2017-12-16 58.0000 14.3400 23.2000
2017-12-17 58.6167 14.0995 23.4333
2017-12-18 58.7500 14.0150 23.4500
2017-12-19 58.5875 14.2555 23.4250
(356, 3)
--- 体重と体脂肪率 ----
平均: 59.935, 14.514
標準偏差: 0.835, 0.478
分散: 0.698, 0.229
共分散: -0.0193105736
相関係数: -0.0483200035
相関係数: -0.0483200035
-------
体重とBMIの相関係数: 0.9980663360
体重とBMIは当然ながら、なす角がほぼゼロであることが分かりました。体重と体脂肪はどうやら相関はなさそうってコトが分かります。。
おつかれさまでした。
まとめ
うーん、Qiitaで数式がつかえるって事でつかってみましたが、気がついたら統計とPythonのはなしになってました。また、$\rm\LaTeX$ で論文を書いてた学生時代を思い出しました。
そして数式かくのはメンドクサイけど、さすがにキレイです。。でもめちゃメンドイ。