LoginSignup
3
1

More than 3 years have passed since last update.

@masatomix(Masatomi KINO)in株式会社プライム・ブレインズ

MNISTの手書き数字の画像セットを、視覚的に見てみる

Last updated at Posted at 2019-04-24

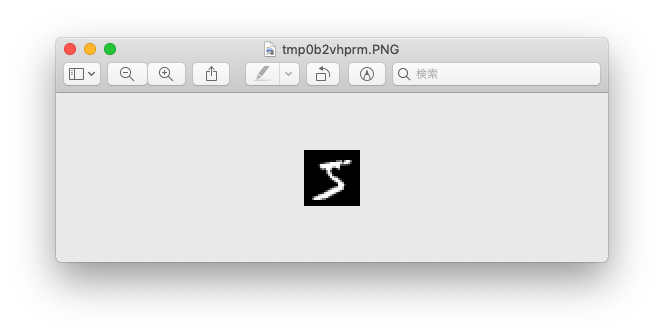
MNISTの手書き数字の画像セットを、視覚的に見てみる

こんな感じに :-)

  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0 51159253159 50  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0 48238252252252237  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0 54227253252239233252 57  6  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0 10 60224252253252202 84252253122  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0163252252252253252252 96189253167  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0 51238253253190114253228 47 79255168  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0 48238252252179 12 75121 21  0  0253243 50  0  0  0  0  0
  0  0  0  0  0  0  0  0 38165253233208 84  0  0  0  0  0  0253252165  0  0  0  0  0
  0  0  0  0  0  0  0  7178252240 71 19 28  0  0  0  0  0  0253252195  0  0  0  0  0
  0  0  0  0  0  0  0 57252252 63  0  0  0  0  0  0  0  0  0253252195  0  0  0  0  0
  0  0  0  0  0  0  0198253190  0  0  0  0  0  0  0  0  0  0255253196  0  0  0  0  0
  0  0  0  0  0  0 76246252112  0  0  0  0  0  0  0  0  0  0253252148  0  0  0  0  0
  0  0  0  0  0  0 85252230 25  0  0  0  0  0  0  0  0  7135253186 12  0  0  0  0  0
  0  0  0  0  0  0 85252223  0  0  0  0  0  0  0  0  7131252225 71  0  0  0  0  0  0
  0  0  0  0  0  0 85252145  0  0  0  0  0  0  0 48165252173  0  0  0  0  0  0  0  0
  0  0  0  0  0  0 86253225  0  0  0  0  0  0114238253162  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0 85252249146 48 29 85178225253223167 56  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0 85252252252229215252252252196130  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0 28199252252253252252233145  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0 25128252253252141 37  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0

概要

さてさて ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 を絶賛学習中。ようやく3.6節の「ニューラルネットワークを用いた手書き数字画像の分類」 です。おもしろくなってきました。

MNISTにて配布されている手書きデータを分類する有名なヤツです。書籍で下記のサンプルコードが紹介されていたので、早速やってみましょう。

https://github.com/oreilly-japan/deep-learning-from-scratch
MITライセンスで公開してくださってます。感謝です。

やるだけなら簡単

Python環境さえあれば、やるだけならホント簡単です。

Pythonの分離環境作成

$ sw_vers
ProductName:    Mac OS X
ProductVersion: 10.14.4
BuildVersion:   18E226
$

$ python --version
Python 3.7.1

$ python -m venv ./venv
$ source ./venv/bin/activate
(venv) $

サンプルコードの実行

先ほどのサイトよりサンプルコードを取得します。

(venv) $ git clone https://github.com/oreilly-japan/deep-learning-from-scratch.git
Cloning into 'deep-learning-from-scratch'...
remote: Enumerating objects: 394, done.
remote: Total 394 (delta 0), reused 0 (delta 0), pack-reused 394
Receiving objects: 100% (394/394), 4.93 MiB | 3.54 MiB/s, done.
Resolving deltas: 100% (204/204), done.

(venv) $ cd deep-learning-from-scratch/ch03/
(venv) $ pip install numpy pillow

さてさて下記は、手書きデータを分類しているコードです。

(venv) $ cat neuralnet_mnist.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p= np.argmax(y) # 最も確率の高い要素のインデックスを取得
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
(venv) $

機械学習済みの重みパラメタ sample_weight.pkl がpickle形式(Pythonのシリアライズファイル) で提供されているので、あとは実行するだけです。

(venv) $ python neuralnet_mnist.py

Downloading train-images-idx3-ubyte.gz ...
Done
Downloading train-labels-idx1-ubyte.gz ...
Done
省略
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ..
...
Done!

Accuracy:0.9352
(venv) $

できました。

もうすこしコードをみてみる

さすがにもうちょっとコードを見てみると、まずxというテスト(分類)したい画像たちを配列として作成し、ひとつの画像x[i]を y = predict(network, x[i]) とやって関数に渡しています。

この関数のなかでは、pickleファイルから復元したニューラルネットワークnetworkからとりだした行列を用いて、行列の積計算とシグモイド関数とソフトマックス関数にかけてyを導出しています。

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3'] # 784x50, 50x100, 100x10 の行列
    b1, b2, b3 = network['b1'], network['b2'], network['b3'] #  50x 1, 100x 1, 10 x 1 の行列
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

このyは「結果が、各分類0から9である確率(1x10の行列)」になっていて、最後に

p = np.argmax(y) # 最も確率の高い要素のインデックスを取得

それらのMax値(一番確率が高い要素)を取り出して、それが予測値だとしています。なるほど。。

細かいことはさておき、とりあえず動きはこんな感じなですね。。

画像データのニューラルネットワークへの渡し方

画像データx[0]の中身

さて付属の下記のコードは、ネットワークに渡される x[0] の中身を表示しています。

(venv) $ cat mnist_show.py
# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
print(label)  # 5

print(img.shape)  # (784,)
img = img.reshape(28, 28)  # 形状を元の画像サイズに変形
print(img.shape)  # (28, 28)

img_show(img)
(venv) $

(venv) $ python mnist_show.py
5
(784,)
(28, 28)
(venv) $

image.png

x[0]は 1x784の行列である、ラベル(答え)は「5」である、などごにょごにょ表示されると同時に、手書きの画像が表示されました。

この1x784行列をもうすこし視覚的に

この行列が画像ってどうゆうことかな？ってことで、もうすこしコードを書いてみてみます。

(venv) $ cat mnist_show_ascii.py
# coding: utf-8
import sys, os

sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
from dataset.mnist import load_mnist

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
print(img.shape)
img = img.reshape(28, 28)  # 形状を元の画像サイズに変形

for i in range(len(img)):
    for j in range(len(img[i])):
        print('{:>4}'.format(img[i][j]), end='')
    print('')

(venv) $ python mnist_show_ascii.py
(784,)
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   3  18  18  18 126 136 175  26 166 255 247 127   0   0   0   0
   0   0   0   0   0   0   0   0  30  36  94 154 170 253 253 253 253 253 225 172 253 242 195  64   0   0   0   0
   0   0   0   0   0   0   0  49 238 253 253 253 253 253 253 253 253 251  93  82  82  56  39   0   0   0   0   0
   0   0   0   0   0   0   0  18 219 253 253 253 253 253 198 182 247 241   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0  80 156 107 253 253 205  11   0  43 154   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0  14   1 154 253  90   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0 139 253 190   2   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0  11 190 253  70   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0  35 241 225 160 108   1   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0  81 240 253 253 119  25   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0  45 186 253 253 150  27   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0  16  93 252 253 187   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0 249 253 249  64   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0  46 130 183 253 253 207   2   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0  39 148 229 253 253 253 250 182   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0  24 114 221 253 253 253 253 201  78   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0  23  66 213 253 253 253 253 198  81   2   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0  18 171 219 253 253 253 253 195  80   9   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0  55 172 226 253 253 253 253 244 133  11   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0 136 253 253 253 212 135 132  16   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0   0
(venv) $

image.png

あー、そういうことですね。

もともと1x784 だった行列 x[0](正確には x_train[0])を28コごとに区切ってならべてみたわけですが、それによって28x28画像の各ピクセルのグレースケールの値を、256段階で表現しているデータであることがわかりました1。

つまりサンプルコードは、28x28ピクセルの画像をフラットに1x784にして、それをニューラルネットワークにかけることで、手書き数字の分類を行っているということがわかりました。

おつかれさまでした。。

関連リンク

  1. 実際はnormalizeといって、255.0で割った値がネットワークには渡されてるようです。 ↩

3
1
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
1