CNTK 2.2 Python API 入門 (4) - LSTM で時系列予測 : IoT データによる太陽光発電出力予測
0. はじめに
◆ CNTK ( Microsoft Cognitive Toolkit ) 2.2 Python API 入門の第4弾です。
今回は LSTM モデルを CNTK で実装して時系列予測問題を扱います。
最初に CNTK におけるシークエンスのコンセプトを説明した後、シミュレーションデータによる時系列予測問題を LSTM ネットワークモデルで解いてみます。そして Internet-of-Things (IoT) データ上で LSTM モデルを活用する例として、ソーラーパネルの日々の発電力量を予測してみます。
前回までの記事 (CNTK 2.2 Python API 入門 (1) 基本, (2) 2 クラス分類, (3) MNIST) で CNTK 2.2 について次のような点がお分かり頂けたかと思います :
- Python API が公開されていて、Python プログラムで深層学習モデルが構築できます。
- 深層学習フレームワークでお馴染みのビルディング・ブロックも多数用意されていて、畳み込みネットワークも簡単に構成できます。
- ネットワーク定義は Python 関数オブジェクトとして実装され、For ループや lambda 記法も利用できる Python ライクな記法で簡潔に定義可能です。
- Trainer クラスでカプセル化したトレーニングの実装も分かりやすく簡潔です。
- CTF フォーマットの利用で CNTK データ・リーダー (= Reader) が簡単に構成できます。
引き続き、CNTK 2.2 Tutorials への橋渡しとなるような CNTK 2.2 Python API の入門記事を作成していきます。
※ Python と機械学習の基本的な知識を持つ読者を想定しています。
※ 他の深層学習フレームワークの経験があれば問題なく読み通せます。
チュートリアル等のプログラムを参考にしながら、分かりやすい構成にして平易な言葉で説明することを心がけました。
入門という位置づけですので基礎理論にも言及はしますがそれは要点のみにとどめて、
CNTK Python API の説明を重視してプログラマ視点から実践的な内容にしています。
※ 初出の API にはリファレンス・マニュアルへリンクを張り、また今回及び前回までの記事で扱った CNTK Python API はまとめてあります。
※ GPU メモリの消費量にも注意を払いました。
内容は :
- 動作環境と Jupyter Notebook について
- 本記事で使用する CNTK Python API
- シークエンスの理解
- LSTM による時系列予測 - 基本 -
- LSTM による時系列予測 - IoT データ -
- What's Next
本記事は以下の CNTK リソース及びチュートリアルを参考にしています :
-
CNTK 106: Part A - Time series prediction with LSTM (Basics)
-
CNTK 106: Part B - Time series prediction with LSTM (IOT Data)
1. 動作環境と Jupyter Notebook について
動作環境
動作環境の構築が必要な場合には、Cognitive Toolkit 2.2 を Azure Linux GPU 仮想マシンにインストール を参考にしてください。Azure ポータルと Ubuntu Linux にある程度慣れていれば、30 分程度で以下のような環境が構築できるかと思います :
- Azure NC 仮想マシン with NVIDIA Tesla® K80 GPU
- Ubuntu 16.04 LTS
- NVIDIA CUDA 8.0 & cuDNN 6.0
- Anaconda 3 4.1.1
- CNTK 2.2 (for GPU)
Jupyter Notebook
また、本記事でも CNTK チュートリアルでも Jupyter Notebook を多用します。
Jupyter Notebook の利用方法については「CNTK 2.2 Python API 入門 (2)」の記事中の Jupyter Notebook の活用 を参照してください。
2. 本記事で使用する CNTK Python API
今回使用する CNTK Python API を先にリストアップしておきます。
前回までに使用した API に本記事で初出の API を追加してまとめました。今回はシークエンスと LSTM (RNN) 関連の API が追加されています。
※ 本記事で初出の API は太字で示されています。
cntk.io パッケージ
| API | 説明 |
|---|---|
CTFDeserializer |
組み込みの deserializer(*) で、CTF (CNTK Text Format) リーダーを構成します。 |
INFINITELY_REPEAT |
全データ sweep (総なめ) のサイズに等しい、ミニバッチ・スケジューリング・ユニットを指定するために使用される定数です。 |
MinibatchSource |
CNTK の Python API 用リーダーです。 |
StreamDef |
deserializer を使用するためにストリームを構成します。 |
StreamDefs |
キーワード引数からレコードを構築します。API というよりも (Python の) 辞書のような働きをします。 |
※ deserializer は外部ストレージからインメモリのシークエンスにデシリアライズ (復号) する機能を持ちます。
cntk.layers パッケージ
cntk.layers.blocks モジュール
| API | 説明 |
|---|---|
LSTM |
recurrence の内側での使用のための LSTM ブロックを作成するための層ファクトリ関数です。 |
cntk.layers.higher_order_layers モジュール
| API | 説明 |
|---|---|
Sequential |
入力上に層のシーケンス (または任意の関数) を適用する合成 (= composite) を作成する層ファクトリ関数です。 |
cntk.layers.layers モジュール
| API | 説明 |
|---|---|
Convolution2D |
2D 畳み込み層を作成する層ファクトリ関数です。 |
Dense |
完全結合線形層のインスタンスを作成するための層ファクトリ関数です。 |
Dropout |
dropout 層を作成するための層ファクトリ関数です。 |
Embedding |
embedding (埋め込み) 層を作成するための層ファクトリ関数です。 |
MaxPooling |
マックス・プーリング層を作成するための層ファクトリ関数です。 |
cntk.layers.sequence モジュール
| API | 説明 |
|---|---|
Recurrence |
RNN, LSTM, そして GRU を含む、リカレント・モデルを実装する層ファクトリ関数です。 |
cntk.learners パッケージ
| API | 説明 |
|---|---|
learning_rate_schedule |
学習率スケジュールを作成します。 |
adam |
モデル・パラメータを学習するために Adam learner インスタンスを作成します。 |
fsadagrad |
モデル・パラメータを学習するために FSAdaGrad learner インスタンスを作成します。 |
sgd |
モデル・パラメータを学習するために SGD learner インスタンスを作成します。 |
UnitType |
schedule の値がサンプル毎上かミニバッチ毎上で指定されるかを示します。 |
cntk.losses パッケージ
| API | 説明 |
|---|---|
cross_entropy_with_softmax (output_vector, target_vector) |
target_vector と output_vector の softmax 間の交差エントロピーを計算します。 |
squared_error |
二乗誤差 - この演算は2つの入力行列の要素間の二乗の差異の総和を計算します。 |
cntk.metrics パッケージ
| API | 説明 |
|---|---|
classification_error (output_vector, target_vector) |
分類エラーを計算します。 |
cntk.ops パッケージ
| API | 説明 |
|---|---|
input_variable |
ネットワークの入力を作成します : 特徴やラベルのようなデータが供給される場所で、いわゆるプレースホルダーです。 |
parameter |
パラメータ・テンソルを作成します。 |
relu |
ReLU 活性化関数です。 |
sigmoid |
sigmoid 活性化関数です。 |
softmax |
softmax 活性化関数です。 |
times |
乗算ですが、この演算の出力は2つの入力行列の積 (= matrix product) です。ブロードキャストをサポートします。 |
cntk.ops.sequence パッケージ
| API | 説明 |
|---|---|
sequence.input_variable |
ネットワークの入力を作成します: 特徴やラベルのようなデータが提供されるべき場所です。 |
sequence.last (seq) |
symbolic 入力シーケンス seq の最後の要素を返します。 |
cntk.tests.test_utils パッケージ
| API | 説明 |
|---|---|
set_device_from_pytest_env() |
Jupyter Notebook 利用時に正しいターゲット・デバイスを選択するためのヘルパー関数です。総ての Jupyter Notebook の開始時にこれを呼び出す必要があります。 |
cntk.train パッケージ
cntk.train.trainer モジュール
| API | 説明 |
|---|---|
Trainer |
モデル・パラメータをトレーニングするクラス。 |
3. シークエンスの理解
LSTM (RNN) を利用するためにはシークエンスの理解が必須ですので、CNTK Web サイトの Working with Sequences を参考にして少し詳しくシークエンスについて説明します。序盤は少し抽象的な話しが多いので初読では分かりにくいかもしれません。その場合はサンプルプログラムの理解に努めて頂ければ良いです。
※ 本章のサンプルコードは Jupyter Notebook からの実行を想定していませんので Notebook への入力は不要です。
3-1 rank と軸
CNTK の入力、出力、そしてパラメータはテンソルとして体系化されています。
各テンソルは rank を持ちます : スカラーは rank 0 のテンソル、ベクトルは rank 1 のテンソル、行列は rank 2 のテンソルです。
これらの異なる個々の次元を軸 (axis) として参照することができます。
総ての CNTK テンソルは幾つかの 静的軸 (static axes) と幾つかの 動的軸 (dynamic axes) を持ちます。
静的軸はネットワークの有効期間 (life) の最初から最後まで同じ長さを保持します。
動的軸はそれらがテンソルに含まれる数値の意味のあるグルーピングを定義するという点では静的軸のようなものですが
しかし :
- それらの長さはインスタンスからインスタンスで変化する可能性があります。
- それらの長さは各ミニバッチが提供される前には概して知られていません。
- それらは順序づけられるかもしれません。
ミニバッチもまたテンソルです。従ってミニバッチは動的軸を持ち (バッチ軸 と呼ばれます)、その長さはミニバッチからミニバッチで変化することがあり得ます。
現時点で CNTK は一つの付加的な動的軸をサポートしています。それは シークエンス軸 としても参照されますが専用名は持ちません。この軸はシークエンスと高レベルの方法で作業することを可能にします。シークエンス上の演算が遂行されるとき、CNTK は2つのシークエンスの結合が常に安全であるかを決定する単純な型チェックを行ないます。
より具体的にするために、2つのサンプルを考えます。
一つ目として、短いビデオ・クリップのミニバッチが CNTK でどのように表現されるかを見てみましょう。
ビデオ・クリップは総て解像度 640x480 で典型的には 3 チャネルでエンコードされるカラーで撮影されていると仮定します。これはミニバッチは長さ 640, 480, そして 3 の3つの静的軸をそれぞれ持っていることを意味します。それはまた2つの動的軸を持ちます : ビデオの長さとミニバッチ軸です。従って、各々が 240 フレーム長の 16 個のビデオのミニバッチは 16 x 240 x 3 x 640 x 480 テンソルとして表わされるでしょう (この場合、16 がバッチ軸で 240 がシークエンス軸です)。
もう一つの例は query (問い合わせ) が与えられたとき文書をランクづけるための学習におけるもので、そこでは動的軸が洗練された解法を提供します。このシナリオの訓練データは典型的には、各 query が関連するドキュメントの可変な数を持つような query のセットから成ります。query-document のペアの各々は関連判断またはラベル (e.g. ドキュメントがその query に関連するか否か) を含みます。各ドキュメントの単語をどのように扱うかに依存してそれらの単語を静的軸か動的軸に置くことができます。それらを静的軸に置くためには、各ドキュメントを、各単語 (または短い句) についてそれがドキュメントに出現する回数の数を要素として含む、語彙のサイズに等しいサイズの (疎な) ベクトルとして扱うことができます。けれどもドキュメントを単語のシークエンスとして処理することもまた可能です、その場合はもう一つの動的軸を使用します。この場合は次のようなネストを持ちます :
- Query: CNTK
- Document 1:
- Microsoft
- Cognitive
- Toolkit
- Document 2:
- Cartoon
- Network
- Document 3:
- NVIDIA
- Microsoft
- Accelerate
- AI
- Document 1:
- Query: flower
- Document 1:
- Flower
- Wikipedia
- Document 2:
- Local
- Florist
- Flower
- Delivery
- Document 1:
最も外側のレベルではバッチ軸です。
ドキュメント・レベルでは動的軸を持つべきです、何故ならば query 毎に候補ドキュメントの可変な数を持つからです。
最も内側のレベルでもまた動的軸を持つべきです、何故ならば各ドキュメントは単語の可変な数を持つからです。
このミニバッチを表わすテンソルもまた一つまたはそれ以上の静的軸を持ちます、これは query とドキュメント内の単語の識別子のような特徴を表わします。
十分に豊富な訓練データにおいてはもう一つのネストレベル、つまりセッションを持つことも可能です、そこでは複数の関連する query が属します。
3-2 シークエンス分類問題
3-2-1 概要
深層学習のもっともエキサイティングな領域の一つがリカレント・ニューラルネットワーク (RNN) 上の様々なアイデアです。
RNN は幾つかの点で深層学習世界の隠れマルコフモデルです。これはパラメータの固定されたセットを使用して可変長のシークエンスを扱うネットワークです。従って入力シークエンスの総ての観測を有限次元のステートに要約することを学習 し、ステートを使用して次の観測を予測し、そして現在のステートと観測された入力で次のステートに変換しなければなりません。換言すれば、情報が存続することを可能にします。
伝統的なニューラルネットワーク層が下の左側の図のようなデータフローを持つと考えられるのに対して、RNN 層は右側の図として見ることが可能です :

右側の図から明らかなように、RNN はシークエンスを扱うための自然な構造です。
これはテキストから音楽、ビデオまで総てを含みます ; 現在のステートが以前のステートに依存しているような任意のものです。
RNN が実にパワフルである一方で、各ステップにおけるそのステートが以前のステートと現在の観測の非線形関数である、"vanilla (普通の・平凡な)" RNN は勾配ベースの方法を通して学習することは極めて厳しいです。学習するためには勾配はネットワークを通してフローバックされる必要があるので、遥かに遅い (後の) 要素における早い要素 (例えば文の開始の単語) からの寄与は、長文の最後の単語の分類の例のように、本質的に消失します。
上述の問題を扱うことは研究の活発な領域です。実際に成功しているように見えるアーキテクチャは Long Short Term Memory (LSTM) ネットワークです。LSTM は極めて有用な RNN の一種で実際に RNN を実装するときに一般にそれを使用します (本記事のサンプルも総て LSTM を利用して実装されます)。LSTM の優位点の良い説明は Understanding LSTM Networks にあります。LSTM は微分可能な関数で、それは入力とステートを取り出力と新しいステートを生成します。
本節であげるサンプル・コードは、シークエンス分類を行なうために LSTM を使用します。
しかしより良い結果を得るために、ここで追加のコンセプトも導入しておきます : 単語埋め込み (word embeddings) です。
伝統的な NLP (自然言語処理) アプローチでは、単語は高次元空間の標準基底で識別されます : 最初の単語は (1, 0, 0, ...)、2番目の単語は (0, 1, 0, ...) 等々 (one-hot エンコーディングとしても知られています)。各単語は他の総てに直交します。
しかしこれは良い抽象ではありません。実際の言語では、幾つかの単語は非常に似ています (それらを同義語と呼びます) あるいはそれらは類似の方法で機能します (e.g. パリ, シアトル, 東京)。キーとなる観察結果は類似のコンテキストで出現する単語は類似しているはずであるということです。各単語を短い学習されたベクトルで表わされることを強制することによってニューラルネットワークにこれらの詳細を分類させることができます。そしてそのタスクでネットワークを上手く動作させるためには単語をこれらのベクトルに効果的にマップすることを学習しなければなりません。例えば、単語 "猫" を表わすベクトルは、ある意味で、"犬" のためのベクトルに幾分近いかもしれません。このタスクではこれらの単語埋め込みをスクラッチから学習します。けれども、数十億の単語を含むコーパス上で訓練された Glove のような事前計算された単語埋め込みで初期化することも可能です。
3-2-2 サンプル・プログラム
単語表現と利用したいリカレント・ニューラルネットワークのタイプが決まれば、シークエンス分類を行なうために使用するネットワークの定義が可能になります。このネットワークは次の層のシリーズを追加していくものと考えることができます :
- Embedding (埋め込み) 層 - 各シークエンスの個々の単語はベクトルになります。
- LSTM 層 - 各単語を以前の単語に依存させることを可能にします。
- Softmax 層 - パラメータの追加のセットでクラスあたりの確率を出力します。
ここでは CNTK Examples に含まれている、以下の短いサンプルプログラム SequenceClassification.py を参考にします。
CNTK におけるシークエンスの利用が容易であることを見てみましょう。
最初にプログラム全体を掲載しますが、本節のサンプルは Jupyter Notebook からの実行を想定していませんので Notebook への入力は不要です :
import os
import cntk as C
import copy
# リーダーを作成します。
def create_reader(path, is_training, input_dim, label_dim):
return C.io.MinibatchSource(C.io.CTFDeserializer(path, C.io.StreamDefs(
features = C.io.StreamDef(field='x', shape=input_dim, is_sparse=True),
labels = C.io.StreamDef(field='y', shape=label_dim, is_sparse=False)
)), randomize=is_training, max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1)
# シークエンス分類のために LSTM モデルを定義します。
def lstm_sequence_classifier(features, num_classes, embedding_dim, LSTM_dim):
classifier = C.layers.Sequential([C.layers.Embedding(embedding_dim),
C.layers.Recurrence(C.layers.LSTM(LSTM_dim)),
C.sequence.last,
C.layers.Dense(num_classes)])
return classifier(features)
# LSTM シークエンス分類モデルを作成して訓練します。
def train_sequence_classifier():
input_dim = 2000 # 語彙
hidden_dim = 25 # LSTM 隠れ及びセル次元
embedding_dim = 50
num_classes = 5
# 特徴とラベル・データを表わす入力変数
features = C.sequence.input_variable(shape=input_dim, is_sparse=True)
label = C.input_variable(num_classes)
# シークエンス分類モデルをインスタンス化します。
classifier_output = lstm_sequence_classifier(features, num_classes, embedding_dim, hidden_dim)
ce = C.cross_entropy_with_softmax(classifier_output, label)
pe = C.classification_error(classifier_output, label)
rel_path = r"../../../../Tests/EndToEndTests/Text/SequenceClassification/Data/Train.ctf"
path = os.path.join(os.path.dirname(os.path.abspath(__file__)), rel_path)
reader = create_reader(path, True, input_dim, num_classes)
input_map = {
features : reader.streams.features,
label : reader.streams.labels
}
lr_per_sample = C.learning_rate_schedule(0.1, C.UnitType.sample)
# モデル訓練を駆動するために trainer オブジェクトをインスタンス化します。
progress_printer = C.logging.ProgressPrinter(0)
trainer = C.Trainer(classifier_output, (ce, pe),
C.sgd(classifier_output.parameters, lr=lr_per_sample),
progress_printer)
# 訓練するためのシークエンスのミニバッチを取得して、そしてモデル訓練を遂行します。
minibatch_size = 200
for i in range(251):
mb = reader.next_minibatch(minibatch_size, input_map=input_map)
trainer.train_minibatch(mb)
evaluation_average = copy.copy(trainer.previous_minibatch_evaluation_average)
loss_average = copy.copy(trainer.previous_minibatch_loss_average)
return evaluation_average, loss_average
if __name__ == '__main__':
# Specify the target device to be used for computing, if you do not want to
# use the best available one, e.g.
# C.try_set_default_device(C.cpu())
error, _ = train_sequence_classifier()
print("Error: %f" % error)
◆ さて、コードの細部を見ていきましょう。
通常のように、最初にモデルのパラメータを設定します。
2000 の語彙 (入力次元)、25 の LSTM 隠れ及びセル次元、次元 50 の embedding 層を持ち、そしてシークエンスの分類のために 5 つの起こりうるクラスを持ちます :
input_dim = 2000 # 語彙
hidden_dim = 25 # LSTM 隠れ及びセル次元
embedding_dim = 50
num_classes = 5
従来通り、特徴とラベルのために一つずつ、2つの入力変数も定義します。
但し、特徴入力はシークエンスであるために C.sequence.input_variable を利用していることに注意してください :
# 特徴とラベル・データを表わす入力変数
features = C.sequence.input_variable(shape=input_dim, is_sparse=True)
label = C.input_variable(num_classes)
そしてモデルをインスタンス化します。lstm_sequence_classifier はモデル定義を含む単純な関数です。
最初に入力を埋め込み行列内で検索して埋め込み表現を返して、それを LSTM リカレント・ニューラルネットワーク層の中を通し、そして LSTM の最後の隠れステートを選択することによって LSTM からの固定長出力を返します。最後に Dense 層で分類します :
# シーケンス分類のために LSTM モデルを定義します。
def lstm_sequence_classifier(features, num_classes, embedding_dim, LSTM_dim):
classifier = C.layers.Sequential([C.layers.Embedding(embedding_dim),
C.layers.Recurrence(C.layers.LSTM(LSTM_dim)),
C.sequence.last,
C.layers.Dense(num_classes)])
return classifier(features)
初出の API をまとめておきましょう :
| API | 説明 |
|---|---|
C.layers.Sequential |
入力に層のシークエンス (または任意の関数) を適用する合成 (= composite) を作成する層ファクトリ関数です。 |
C.layers.Embedding |
embedding (埋め込み) 層を作成するための層ファクトリ関数です。 |
C.layers.Recurrence |
RNN, LSTM, そして GRU を含む、リカレント・モデルを実装する層ファクトリ関数です。 |
C.layers.LSTM |
recurrence の内側での使用のための LSTM ブロックを作成するための層ファクトリ関数です。 |
C.sequence.last (seq) |
symbolic 入力シーケンス seq の最後の要素を返します。 |
次に、これも従来通り、ラベルをどの程度上手く分類できたかを計るノードを設定します :
ce = C.cross_entropy_with_softmax(classifier_output, label)
pe = C.classification_error(classifier_output, label)
そして組み込みの deserializer を使用してリーダーを作成します。
deserializer は外部ストレージからインメモリのシーケンスにデシリアライズ (復号) する機能を持ちます :
def create_reader(path, is_training, input_dim, label_dim):
return C.io.MinibatchSource(C.io.CTFDeserializer(path, C.io.StreamDefs(
features = C.io.StreamDef(field='x', shape=input_dim, is_sparse=True),
labels = C.io.StreamDef(field='y', shape=label_dim, is_sparse=False)
)), randomize=is_training, max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1)
ここで、CTF リーダーは可変長のシークエンスを扱える ことに注意しましょう。
ストリームを構成する StreamDef でフィールド名として x, y が指定されていますが、
入力用のサンプルデータ (Train.ctf) の内容を見て確認しておきましょう :
-
yがサイズ 5 の one-hot ベクトルでエンコードされていることはすぐに分かると思います。 - 最初のカラムはシークエンス ID です。
-
xは疎ベクトルで表現されています。従って、|x 560:1はインデックス 560th の値が 1 であることを示しています :
$ head -n 20 Train.ctf
0 |x 560:1 |y 1 0 0 0 0
0 |x 0:1
0 |x 0:1
1 |x 560:1 |y 1 0 0 0 0
1 |x 0:1
1 |x 0:1
1 |x 424:1
2 |x 208:1 |y 0 0 0 0 1
2 |x 508:1
2 |x 1185:1
2 |x 8:1
2 |x 0:1
3 |x 0:1 |y 0 0 0 1 0
3 |x 0:1
3 |x 0:1
4 |x 208:1 |y 0 1 0 0 0
4 |x 64:1
4 |x 0:1
4 |x 573:1
5 |x 0:1 |y 0 1 0 0 0
$ tail -n 15 Train.ctf
1243 |x 0:1
1243 |x 573:1
1244 |x 0:1 |y 1 0 0 0 0
1244 |x 811:1
1244 |x 0:1
1245 |x 0:1 |y 0 0 1 0 0
1245 |x 1134:1
1245 |x 1243:1
1245 |x 8:1
1245 |x 0:1
1246 |x 1481:1 |y 0 1 0 0 0
1246 |x 432:1
1246 |x 1631:1
1246 |x 0:1
1246 |x 0:1
後は簡単です。訓練を駆動する trainer オブジェクトをインスタンス化した後、訓練ループを回すだけです。
学習率 0.1 で基本的なオプティマイザ SGD を使用しています。ミニバッチのサイズは 200 です。
このサンプル・プログラムを実行すると以下のような出力を生成します :
$ python SequenceClassification.py
Selected GPU[0] Tesla K80 as the process wide default device.
-------------------------------------------------------------------
Build info:
Built time: Sep 15 2017 07:30:54
Last modified date: Fri Sep 15 04:28:48 2017
Build type: release
Build target: GPU
With 1bit-SGD: no
With ASGD: yes
Math lib: mkl
CUDA version: 8.0.0
CUDNN version: 6.0.21
Build Branch: HEAD
Build SHA1: 23878e5d1f73180d6564b6f907b14fe5f53513bb
MPI distribution: Open MPI
MPI version: 1.10.7
-------------------------------------------------------------------
average since average since examples
loss last metric last
------------------------------------------------------
Learning rate per 1 samples: 0.1
1.61 1.61 0.841 0.841 44
1.62 1.62 0.722 0.663 133
1.43 1.29 0.563 0.448 316
1.32 1.23 0.485 0.418 682
1.29 1.27 0.466 0.447 1402
1.27 1.25 0.462 0.459 2862
1.21 1.15 0.439 0.417 5776
Error: 0.200000
これが、シークエンス分類のための先端技術の基本モデルで、膨大な訓練データでスケールすることが可能です。
訓練データのサイズが大きくなるにつれて、隠れ次元の数を増やして LSTM に更なるキャパシティを与える必要があります。
また LSTM の層を積むことによって、より複雑なネットワークを得ることもできます。
3-3 シークエンスを NumPy で供給する
CNTK は多くの細部 (ランダム化, 事前読込み, メモリ消費の削減 etc.) の面倒を見てくれる非常に効率的な組み込みリーダーを持ちますが、その一方で貴方のデータが既に NumPy 配列にある場合もあるでしょう。このようなケースで入力のシークエンスをどのように指定してシークエンスのミニバッチをどのように指定するかを知ることは重要です。
ここでは画像を例に取ります。
各シークエンスはそれ自身が NumPy 配列でなければなりません。
もし次のような小さいカラー画像を表わす入力変数を持つのであれば :
x = sequence.input_variable((3,32,32))
そして img1 から img4 の 4 画像のシークエンスを CNTK に供給することを望むのであれば、総ての 4 画像を含むテンソルを作成する必要があります。
例えば :
img_seq = np.stack([img1, img2, img3, img4])
output = network.eval({x:[img_seq]})
NumPy の stack 関数は入力を新しい軸 (デフォルトでそれを最初に配置します) に沿って積みますので、img_seq の shape は $4\times3\times32\times32$ になります。
img_seq を x にバインドする前にそれをリストにラップしたことに気がついたかもしれません。 このリストは 1 のミニバッチを表わしていてそしてミニバッチはリストとして指定されます。その理由はミニバッチの異なる要素は異なる長さを持てるからです。
もしミニバッチの総ての要素が同じ長さのシークエンスならば次元 $b \times s \times d_{1} \times \dots \times d_{k}$ の一つの大きなテンソルとしてミニバッチを提供することも容認できます。ここで $b$ はバッチサイズ、$s$ はシーケンスの長さ、そして $d_{i}$ は入力変数の i-th 静的軸の次元です。
4. LSTM による時系列予測 - 基本 -
シークエンスの概念をある程度把握出来たところで、本記事の主題である LSTM による時系列予測の章に入ります。
まず基本編では、連続関数を利用したシミュレーション・データをベースに予測モデルを実装します。
※ 本章からは Jupyter Notebook の利用を想定しています。
4-1 概要
時系列において未来値を予測するために CNTK で LSTM をどのように使用するかを示します。
問題設定
連続関数 - 具体的には正弦波 (sin 波) を使用してシミュレートされたデータセットを利用します。
$y = sin(t)$ 関数 ($y$ は時間 $t$ で観測された振幅の信号) の過去の N 個の値から、M 個離れた対応する未来の時刻ポイントのための $y$ の値を予測します。
LSTM は経験から学習する能力がありますので、このタスクのために良く適合します。
※ ここで Jupyter Notebook の新しいノートブックを作成して使用していきましょう。
from IPython.display import Image
Image(url="http://www.cntk.ai/jup/sinewave.jpg")

本章は次の流れに沿って説明していきます :
- シミュレートされたデータ生成
- LSTM ネットワーク・モデリング
- モデル訓練と評価
では、始めましょう。
インポート
従来通りですが、データ分析ライブラリ: pandas を pd としてインポートしていることに注意しましょう :
import math
from matplotlib import pyplot as plt
import numpy as np
import os
import pandas as pd
import time
import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # (only needed for our build system)
%matplotlib inline
便宜上、2つの実行モードがあります :
-
Fast モード:
isFastをTrueに設定します。
デフォルト・モードで、より少ない反復で訓練するか限定されたデータで訓練/テストすることを意味します。
これは機能的な正当性という意味では確かなものですが、生成されたモデルは完全な訓練によって生成されたものからはかけ離れています。 -
Slow モード:
実装に精通した後、異なるパラメータ等でより長い時間、訓練を実行することで洞察を得ることを望むのであれば、このフラグをFalseに設定してください。
isFast = True
※ 両方のモードで試していますので、訓練/評価の結果は併記していきます。
4-2 データ生成
シミュレートされた正弦波データを生成するために、2つのヘルパー関数を作成します。
先に split_data() 関数を定義します。名前が示すように、データを訓練、検証そしてテストセットに分割します :
def split_data(data, val_size=0.1, test_size=0.1):
"""
np.array を訓練、検証そしてテスト用に分割します。
"""
pos_test = int(len(data) * (1 - test_size))
pos_val = int(len(data[:pos_test]) * (1 - val_size))
train, val, test = data[:pos_val], data[pos_val:pos_test], data[pos_test:]
return {"train": train, "val": val, "test": test}
◆ そしてデータ生成を担う generate_data() を定義します。
モデルへの入力として sin 関数の N 個の連続的な値をサンプリングします。そしてその各々のサンプリングの最後の観測値から M ステップ離れた未来値をモデルを利用して予測することを目標とします。訓練データとして、そのような各々のサイズが N の入力信号の複数のインスタンスと、それに対応する望ましい出力を生成します。
このことから、$k$ = バッチサイズとすれば、generate_data 関数は下に示すような $X$ と対応する $L$ データを生成して NumPy 配列を返します :
- LSTM への入力セット ($X$) :
$$ X = [{y_{11}, y_{12}, \cdots , y_{1N}},
{y_{21}, y_{22}, \cdots, y_{2N}}, \cdots,
{y_{k1}, y_{k2}, \cdots, y_{kN}}]$$
上のサンプル $y_{i,j}$ で、$N$ 個の時刻ウィンドウ内における $i^{th}$ バッチと $j^{th}$ 時刻ポイントのための観測された関数値を表わしています。
- すると未来の望ましい出力 ($L$) は次のように表現されます :
$$ L = [ {y_{1,N+M}}, {y_{2,N+M}}, \cdots, {y_{k,N+M}}]$$
◆ 上述の説明は少し抽象的で分かりにくいかもしれませんので、実装コードで具体的に確認していきます :
def generate_data(fct, x, time_steps, time_shift):
"""
RNN へ供給するための fct(x) 関数に対応するシークエンスを生成します。
"""
data = fct(x)
if not isinstance(data, pd.DataFrame):
data = pd.DataFrame(dict(a = data[0:len(data) - time_shift],
b = data[time_shift:]))
rnn_x = []
for i in range(len(data) - time_steps + 1):
rnn_x.append(data['a'].iloc[i: i + time_steps].as_matrix())
rnn_x = np.array(rnn_x)
# LSTM モデルで必要とされる入力と互換性があるように
# row から columns へデータを reshape または rearrange します。
# モデルは与えられたバッチにおいて時刻ポイント あたり 1 float を期待します。
rnn_x = rnn_x.reshape(rnn_x.shape + (1,))
rnn_y = data['b'].values
rnn_y = rnn_y[time_steps - 1 :]
# 入力 shape にマッチするように row から columns へデータを Reshape または rearrange します。
rnn_y = rnn_y.reshape(rnn_y.shape + (1,))
return split_data(rnn_x), split_data(rnn_y)
ここでは fct は sin 関数です。(x 軸の定義域としての) 等間隔に順序付けられた数列を持つ NumPy 配列 x が渡されたら最初に sin(x) を計算します。そしてその計算結果である data 配列を加工した a, b から pandas のデータフレーム・オブジェクトを作成します。
※ pandas のデータフレームは表計算ソフトの機能をカプセル化したオブジェクトです (データフレームという名前は (おそらく) R から派生しています)。
以下は a, b のデバッグ・プリントですが、a は data をそのまま流用していて b は前方に M ステップずらしていることが分かります。つまり a を観測値、b を未来値として利用するわけです :
a b
0 0.000000 0.049984
1 0.010001 0.059970
2 0.020001 0.069950
3 0.029998 0.079923
4 0.039993 0.089888
5 0.049984 0.099843
6 0.059970 0.109789
7 0.069950 0.119724
8 0.079923 0.129647
9 0.089888 0.139557
10 0.099843 0.149453
...
入力特徴 rnn_x は a を元にして N (= 5) 個ずつまとめます :
[[ 0. 0.01000083 0.02000067 0.0299985 0.03999333]
[ 0.01000083 0.02000067 0.0299985 0.03999333 0.04998416]
[ 0.02000067 0.0299985 0.03999333 0.04998416 0.05997 ]
...,
[-0.59797573 -0.58993524 -0.58182967 -0.57366586 -0.56544465]
[-0.58993524 -0.58182967 -0.57366586 -0.56544465 -0.55716687]
[-0.58182967 -0.57366586 -0.56544465 -0.55716687 -0.54883337]]
そして LSTM モデルの入力仕様に合わせて reshape します :
[[[ 0. ]
[ 0.01000083]
[ 0.02000067]
[ 0.0299985 ]
[ 0.03999333]]
[[ 0.01000083]
[ 0.02000067]
[ 0.0299985 ]
[ 0.03999333]
[ 0.04998416]]
[[ 0.02000067]
[ 0.0299985 ]
[ 0.03999333]
[ 0.04998416]
[ 0.05997 ]]
...,
[[-0.59797573]
[-0.58993524]
[-0.58182967]
[-0.57366586]
[-0.56544465]]
[[-0.58993524]
[-0.58182967]
[-0.57366586]
[-0.56544465]
[-0.55716687]]
入力ラベル rnn_y は単純です :
[ 0.08988751 0.09984337 0.10978924 ..., -0.52351326 -0.51496518
-0.50636566]
やはり入力仕様に合わせます :
[[ 0.08988751]
[ 0.09984337]
[ 0.10978924]
...,
[-0.52351326]
[-0.51496518]
[-0.50636566]]
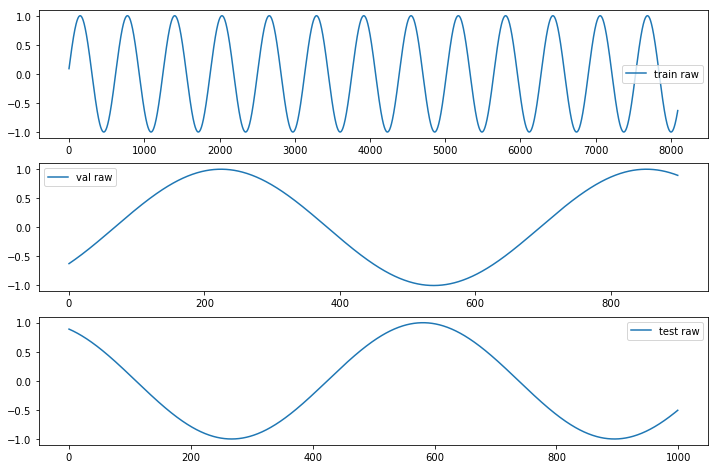
◆ ここで実際にデータを生成します。併せて、生成されたデータを安直にプロットして可視化してみましょう :
N = 5 # 入力: N 個の連続する値
M = 5 # 出力: M ステップ先の1つの値を予測します
X, Y = generate_data(np.sin, np.linspace(0, 100, 10000, dtype=np.float32), N, M)
f, a = plt.subplots(3, 1, figsize=(12, 8))
for j, ds in enumerate(["train", "val", "test"]):
a[j].plot(Y[ds], label=ds + ' raw');
[i.legend() for i in a];
4-3 ネットワーク・モデリング
さて、モデル作成に入ります。3 章でシークエンス分類のために作成したモデルと類似のものですが、ここでは embedding 層は必要ありません。
それぞれの入力シークエンスは N 個の入力値を持ち、これらは連続関数の値です。
個々の入力値に対して1つの LSTM セルを持つようなネットワークをセットアップします。
LSTM からの N 個の出力は、単一の出力を生成する Dense 層への入力です。
入力は LSTM リカレント・ニューラルネットワーク層の中を通されて、そして LSTM の最後の隠れステートを選択することで LSTM から固定長出力を返します。最後に単一の出力を生成する Dense 層に渡されます。
LSTM と Dense 層の間には Dropout 層を挿入します、これは無作為に値の 20 % をドロップして訓練データセットへモデルをオーバーフィッティングさせることを LSTM に回避させます。訓練の間は Dropout 層を使用しますが、予測を行なうためにモデルを使用するときは値を drop はしません :
def create_model(x):
"""時系列予測のためのモデルを作成します。"""
with C.layers.default_options(initial_state = 0.1):
m = C.layers.Recurrence(C.layers.LSTM(N))(x)
m = C.sequence.last(m)
m = C.layers.Dropout(0.2, seed=1)(m)
m = C.layers.Dense(1)(m)
return m
3 章で既出ですが、改めて API をまとめておきます :
| API | 説明 |
|---|---|
C.layers.Sequential |
入力上に層のシーケンス (または任意の関数) を適用する合成 (composite) を作成する層ファクトリ関数です。 |
C.layers.Recurrence |
RNN, LSTM, そして GRU を含む、リカレント・モデルを実装する層ファクトリ関数です。 |
C.layers.LSTM |
recurrence の内側での使用のための LSTM ブロックを作成するための層ファクトリ関数です。 |
C.sequence.last (seq) |
symbolic 入力シーケンス seq の最後の要素を返します。 |
4-4 ネットワークをトレーニングする
バッチを生成して訓練関数に供給する、next_batch() イテレータを定義します :
def next_batch(x, y, ds):
"""処理するための次のバッチを取得します。"""
def as_batch(data, start, count):
part = []
for i in range(start, start + count):
part.append(data[i])
return np.array(part)
for i in range(0, len(x[ds])-BATCH_SIZE, BATCH_SIZE):
yield as_batch(x[ds], i, BATCH_SIZE), as_batch(y[ds], i, BATCH_SIZE)
念のために、バッチの形状を確認しておきましょう。まずは特徴入力です :
[[[ 0. ]
[ 0.01000083]
[ 0.02000067]
[ 0.0299985 ]
[ 0.03999333]]
[[ 0.01000083]
[ 0.02000067]
[ 0.0299985 ]
[ 0.03999333]
[ 0.04998416]]
[[ 0.02000067]
[ 0.0299985 ]
[ 0.03999333]
[ 0.04998416]
[ 0.05997 ]]
[[ 0.0299985 ]
[ 0.03999333]
[ 0.04998416]
[ 0.05997 ]
[ 0.06994984]]
[[ 0.03999333]
[ 0.04998416]
[ 0.05997 ]
[ 0.06994984]
[ 0.07992267]]
...
そしてラベル入力です :
[[ 0.08988751]
[ 0.09984337]
[ 0.10978924]
[ 0.11972412]
[ 0.12964703]
...
◆ モデルを訓練するために必要な他の総てのものをセットアップします。
訓練パラメータの定義、入力、出力、モデルとオプティマイザ、更には損失関数を定義します :
# 訓練パラメータ
TRAINING_STEPS = 10000
BATCH_SIZE = 100
EPOCHS = 10 if isFast else 100
# 入力シークエンス
x = C.sequence.input_variable(1)
# モデルを作成します。
z = create_model(x)
# 期待される出力 (ラベル) です、またモデル出力の動的軸はラベル入力のモデルとして指定されます。
l = C.input_variable(1, dynamic_axes=z.dynamic_axes, name="y")
# 学習率
learning_rate = 0.02
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
# 損失関数
loss = C.squared_error(z, l)
# エラーを決定するために二乗誤差を使用します。
error = C.squared_error(z, l)
# fsadagrad オプティマイザを使用します。
momentum_time_constant = C.momentum_as_time_constant_schedule(BATCH_SIZE / -math.log(0.9))
learner = C.fsadagrad(z.parameters,
lr = lr_schedule,
momentum = momentum_time_constant,
unit_gain = True)
trainer = C.Trainer(z, (loss, error), [learner])
◆ 訓練する準備ができました。実行してみましょう。100 エポックで容認できる結果を生みます :
loss_summary = []
start = time.time()
for epoch in range(0, EPOCHS):
for x1, y1 in next_batch(X, Y, "train"):
trainer.train_minibatch({x: x1, l: y1})
if epoch % (EPOCHS / 10) == 0:
training_loss = trainer.previous_minibatch_loss_average
loss_summary.append(training_loss)
print("epoch: {}, loss: {:.5f}".format(epoch, training_loss))
print("training took {0:.1f} sec".format(time.time() - start))
epoch: 0, loss: 0.47786
epoch: 1, loss: 0.13716
epoch: 2, loss: 0.09105
epoch: 3, loss: 0.06731
epoch: 4, loss: 0.07279
epoch: 5, loss: 0.05649
epoch: 6, loss: 0.07282
epoch: 7, loss: 0.05344
epoch: 8, loss: 0.05083
epoch: 9, loss: 0.03765
training took 2.7 sec
Slow モードについても試してあります :
epoch: 0, loss: 0.47786
epoch: 10, loss: 0.03878
epoch: 20, loss: 0.02528
epoch: 30, loss: 0.03829
epoch: 40, loss: 0.05250
epoch: 50, loss: 0.03531
epoch: 60, loss: 0.02825
epoch: 70, loss: 0.03521
epoch: 80, loss: 0.04200
epoch: 90, loss: 0.04303
training took 23.6 sec
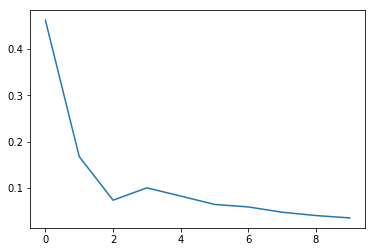
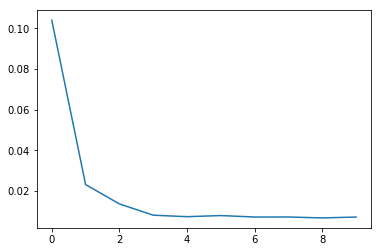
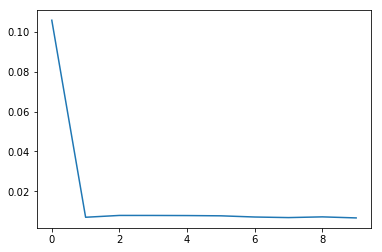
モデルが収束する様子を損失関数が示していることを可視化して確認します :
plt.plot(loss_summary, label='training loss');
通常は検証のために取り分けておいたデータ上で訓練を検証しますが、入力データが小さいのでデータセットの総てのパーツの上で検証を実行します :
def get_mse(X,Y,labeltxt):
result = 0.0
for x1, y1 in next_batch(X, Y, labeltxt):
eval_error = trainer.test_minibatch({x : x1, l : y1})
result += eval_error
return result/len(X[labeltxt])
# 訓練と検証データセット上のエラーを出力表示します。
for labeltxt in ["train", "val"]:
print("mse for {}: {:.6f}".format(labeltxt, get_mse(X, Y, labeltxt)))
mse for train: 0.000059
mse for val: 0.000048
mse for train: 0.000024
mse for val: 0.000022
平均二乗誤差で比較すると、Fast モードと Slow モードでかなりの差が出ています。
# テストセット上のエラーを出力表示します。
labeltxt = "test"
print("mse for {}: {:.6f}".format(labeltxt, get_mse(X, Y, labeltxt)))
mse for test: 0.000052
mse for test: 0.000023
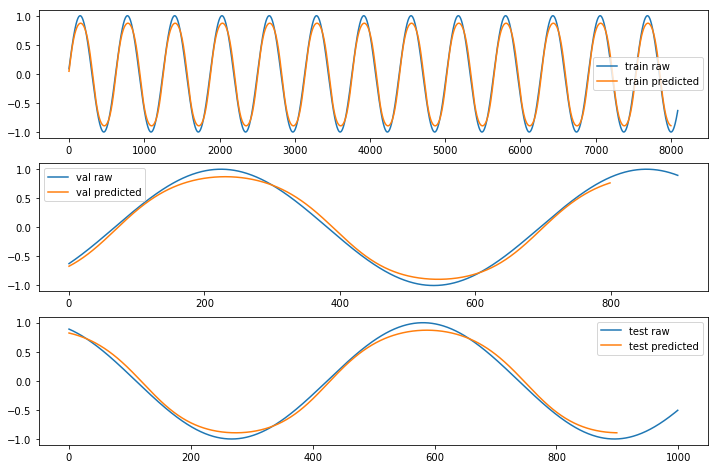
◆ 単純な LSTM アプローチでどの程度上手く予測しているかを確認するために、期待される出力 (Y) とモデルが作成した予測をプロットしてみます :
# predict
f, a = plt.subplots(3, 1, figsize = (12, 8))
for j, ds in enumerate(["train", "val", "test"]):
results = []
for x1, y1 in next_batch(X, Y, ds):
pred = z.eval({x: x1})
results.extend(pred[:, 0])
a[j].plot(Y[ds], label = ds + ' raw');
a[j].plot(results, label = ds + ' predicted');
[i.legend() for i in a];
Fast モード :
モデルの単純さを考慮すれば、完全ではありませんが十分に近いと言えます。振幅の大きさが少し小さいでしょうか。
この結果を改善するためには :
- より多くのデータポイントで訓練する。
- モデルをより多くのエポックで訓練する。
- あるいはモデルそれ自身を改良する。
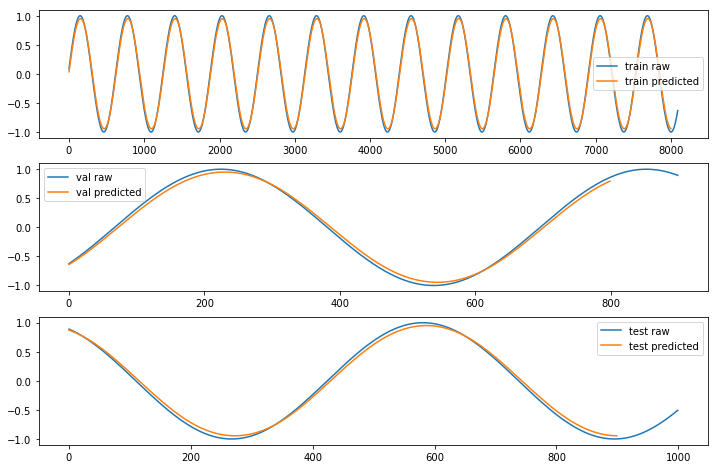
ここでは、Slow モードで確認してみましょう。振幅の大きさも含めて大きく改善しました :
GPU メモリ使用量
トレーニング後の GPU メモリ使用量を確認しておきます。
消費量は非常に小さいもので、Fast モードでも Slow モードでも違いはありませんでした :
$ nvidia-smi
Sat Oct 14 14:15:16 2017
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.66 Driver Version: 384.66 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla K80 Off | 0000214E:00:00.0 Off | 0 |
| N/A 42C P0 72W / 149W | 98MiB / 11439MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 9297 C /home/masao/anaconda3/bin/python 87MiB |
+-----------------------------------------------------------------------------+
$ nvidia-smi
Sat Oct 14 14:22:48 2017
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.66 Driver Version: 384.66 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla K80 Off | 0000214E:00:00.0 Off | 0 |
| N/A 46C P0 71W / 149W | 98MiB / 11439MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 26825 C /home/masao/anaconda3/bin/python 87MiB |
+-----------------------------------------------------------------------------+
5. LSTM による時系列予測 - IoT データ -
4 章では連続関数のシミュレーションデータによる時系列予測問題を LSTM ネットワークモデルで解いてみました。
本章では現実の世界の Internet-of-Things (IoT) データ上で LSTM モデルを活用することを考えます。
具体的には、ソーラーパネルの日々の発電力量を当日の初期読み取り値を元に予測してみます。
5-1 概要
太陽光発電出力予測 ( Solar power forecasting ) は挑戦的で重要な問題です。
この問題は天気変数予測の問題と密接に絡んでいます。通常はこの問題は2つのパートに分割され、ソーラー PV (太陽光発電) や個々の気象変数にフォーカスする一方で、見積もられた気象リソースで具体的なパワープラントが生成するエネルギー総量を見積もります。
けれどもここでは話しを簡単にして、未来値を予測するために
過去にソーラーパネルから生成された IoT データをベースにして単純化された LSTM 予測モデルを扱います。
目標
ソーラーパネルの過去の (daily で 30 分毎に記録された) 発電出力データを使用して、当日のソーラーパネルの発電力量を予測します。
当日の初期読み取り値 (= initial readings) を元にソーラーパネルの日々の発電力量を予測するために LSTM ベースの時系列予測モデルを使用します。最初の 2 値(*) を読み取った後で予測を開始して、その後の個々の新しい読み取り値で予測を調整していくことになります。
※ 今回の例題では、最初の 2 値とは朝 7:00 と 7:30 の読み取り値を指します。
本章も次の流れに沿って進めます :
- データ生成
- LSTM ネットワークモデリング
- モデル訓練と評価
◆ では始めましょう。Jupyter Notebook の新しいノートブックを作成して使用しましょう :
from matplotlib import pyplot as plt
import math
import numpy as np
import os
import pandas as pd
import random
import time
import cntk as C
try:
from urllib.request import urlretrieve
except ImportError:
from urllib import urlretrieve
%matplotlib inline
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # (only needed for our build system)
# to make things reproduceable, seed random
np.random.seed(0)
4 章と同様に、便宜上、2つの実行モードがあります :
-
Fast モード:
isFastをTrueに設定します。
デフォルト・モードで、より少ない反復で訓練するか限定されたデータで訓練/テストすることを意味します。
これは機能的な正当性という意味では確かなものですが、生成されたモデルは完全な訓練によって生成されたものからはかけ離れています。 -
Slow モード:
実装に精通した後、異なるパラメータ等でより長い時間、訓練を実行することで洞察を得ることを望むのであれば、このフラグをFalseに設定してください。
Fast モードでは 100 エポック訓練します。精度は低いかもしれませんがモデルの正当性を確認するためには十分です。
良い精度を得るためには 1000-2000 エポックの訓練が必要です。
※ 両方のモードで試していますので、訓練/評価の結果は併記していきます。
isFast = True
# we need around 2000 epochs to see good accuracy. For testing 100 epochs will do.
EPOCHS = 100 if isFast else 2000
5-2 データ前処理、及びシークエンス生成
データ概要
例題のソーラーパネルは、30 分毎の間隔で2種類の計測値を出力します :
-
solar.currentは、現在の発電力 (単位: ワット) -
solar.totalは、ここまでの時刻で当日のために発電された総量、発電力量 (単位 : ワット時)
モデル入力用のシークエンスは solar.total の値を元にして作成することになります。
今回の予測アプローチは当日の最初の 2 初期読み取りから開始します。これらの読み取り値をベースに予測を開始して個々の新しい読み取り値で予測を調整します。
使用する訓練データセットは3年間の間捕獲されたデータを含み guschmueds.blob.core.windows.net/datasets/solar.csv で見つかります。
このデータセットは前処理されていません: つまり生データで小さなずれや欠落 (gaps) とエラーを含みます。エラーはソーラーパネルがレポートに失敗するようなケースです。
csv ファイルは次のようなフォーマットを持っています :
$ head -n 10 solar.csv
time,solar.current,solar.total
2013-12-01 07:00:00,6.300000190734863,1.690000057220459
2013-12-01 07:30:00,44.29999923706055,11.359999895095825
2013-12-01 08:00:00,208.0,67.5
2013-12-01 08:30:00,482.0,250.5
2013-12-01 09:00:00,774.0,573.5
2013-12-01 09:30:00,1010.5,1029.5
2013-12-01 10:00:00,1220.0,1575.0
2013-12-01 10:30:00,1460.0,2285.0
2013-12-01 11:00:00,1545.0,3020.0
...
前処理 (シークエンス生成)
データの前処理として、generate_solar_data() 関数が pandas ライブラリを利用して次のタスクを遂行します :
- 生データを csv ファイルから pandas データフレームに読み込みます。
- データを正規化します。
- 日付でグループ化します。
- カラム
solar.current.maxとsolar.total.maxを追加します。 - 各日にちに対してシークエンスを生成します。
総てのシークエンスはシークエンスの単一のリストに結合されます。従って入力ではタイムスタンプの概念は消失していて、シークエンスだけの問題となります。
【注意点】
- 一日につき 8 データポイントよりも少ないデータポイントしか持たない場合は、生データに何かが欠けていると仮定してその日についてはスキップします。
- 一日に 14 データポイントより多く得た場合には読み取り (= readings) を切り詰めます。
以下が generate_solar_data() 関数の実装です :
def generate_solar_data(input_url, time_steps, normalize=1, val_size=0.1, test_size=0.1):
"""
ソーラーパネル・データを持つデータフレームをベースに、RNN に供給するシークセンスを生成します。
cvs のフォーマットは : time ,solar.current, solar.total
"""
# ローカルでデータファイルを探します。存在しない場合にはダウンロードします。
cache_path = os.path.join("data", "iot")
cache_file = os.path.join(cache_path, "solar.csv")
if not os.path.exists(cache_path):
os.makedirs(cache_path)
if not os.path.exists(cache_file):
urlretrieve(input_url, cache_file)
print("downloaded data successfully from ", input_url)
else:
print("using cache for ", input_url)
# 'time' カラムをインデックスにして csv ファイルからデータフレームを作成します。
df = pd.read_csv(cache_file, index_col="time", parse_dates=['time'], dtype=np.float32)
df["date"] = df.index.date
# データを正規化します。
df['solar.current'] /= normalize
df['solar.total'] /= normalize
# 日にちでグループ化し、日毎の max を見つけてそして新しいカラム .max を追加します。
grouped = df.groupby(df.index.date).max()
grouped.columns = ["solar.current.max", "solar.total.max", "date"]
# 連続する読み取り値と日毎の max 値を単一のフレームにマージします。
df_merged = pd.merge(df, grouped, right_index=True, on="date")
df_merged = df_merged[["solar.current", "solar.total",
"solar.current.max", "solar.total.max"]]
# 日にちでグループ化したので一度に一日を処理できます。
grouped = df_merged.groupby(df_merged.index.date)
per_day = []
for _, group in grouped:
per_day.append(group)
# データセットを訓練、検証そしてテストセットに日にちの境界で分割します。
val_size = int(len(per_day) * val_size)
test_size = int(len(per_day) * test_size)
next_val = 0
next_test = 0
result_x = {"train": [], "val": [], "test": []}
result_y = {"train": [], "val": [], "test": []}
# 一日あたりのシークエンスを一度に生成します。
for i, day in enumerate(per_day):
# 一日のために 8 データポイントより少なく持つ場合はその日に渡ってスキップします。
# 生データに何かが欠けていると仮定します。
total = day["solar.total"].values
if len(total) < 8:
continue
if i >= next_val:
current_set = "val"
next_val = i + int(len(per_day) / val_size)
elif i >= next_test:
current_set = "test"
next_test = i + int(len(per_day) / test_size)
else:
current_set = "train"
max_total_for_day = np.array(day["solar.total.max"].values[0])
for j in range(2, len(total)):
result_x[current_set].append(total[0:j])
result_y[current_set].append([max_total_for_day])
if j >= time_steps:
break
# result_y を NumPy 配列にします。
for ds in ["train", "val", "test"]:
result_y[ds] = np.array(result_y[ds])
return result_x, result_y
詳細は後回しにして、取り敢えず csv ファイルを実際にダウンロードしてデータセットを生成します :
# 一日に 14 入力まで保持します。
TIMESTEPS = 14
# 20000 はデータセットの最大のトータル出力です。
# この値で総ての値を正規化しますので入力は 0.0 と 1.0 の範囲の間です。
NORMALIZE = 20000
X, Y = generate_solar_data("https://www.cntk.ai/jup/dat/solar.csv",
TIMESTEPS, normalize=NORMALIZE)
downloaded data successfully from https://www.cntk.ai/jup/dat/solar.csv
※ csv ファイルは Jupyter Notebook の実行ディレクトリ下、data/iot/solar.csv ファイルに保存されます。
データフォーマット
この時点で LSTM に供給するシークエンスを確認することができます :
X['train'][0:3]
[array([ 0. , 0.0006985], dtype=float32),
array([ 0. , 0.0006985, 0.0033175], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 ], dtype=float32)]
Y['train'][0:3]
array([[ 0.23899999],
[ 0.23899999],
[ 0.23899999]], dtype=float32)
◆ 上の generate_solar_data() 関数定義のコードブロックだけでは分かりにくいと思いますので、関数の動作を直感的に把握するために中間値を出力して確認してみましょう。
ここでは 2013-12-03 のデータに着目していきます :
(1) まずはデータファイル solar.csv をダンプしてみます。カラム名として time, solar.current, solar.total を持つ通常の csv ファイルです :
$ wc -l solar.csv
25370 solar.csv
$ head -n 100 solar.csv
time,solar.current,solar.total
...
2013-12-03 07:00:00,0.11999999731779099,0.0
2013-12-03 07:30:00,59.5,13.970000147819519
2013-12-03 08:00:00,119.5,66.35000038146973
2013-12-03 08:30:00,571.5,207.5
2013-12-03 09:00:00,843.0,545.5
2013-12-03 09:30:00,689.0,1010.0
2013-12-03 10:00:00,853.5,1360.0
2013-12-03 10:30:00,599.5,1745.0
2013-12-03 11:00:00,691.0,2045.0
2013-12-03 11:30:00,684.5,2410.0
2013-12-03 12:00:00,559.0,2700.0
2013-12-03 12:30:00,703.5,3010.0
2013-12-03 13:00:00,620.5,3360.0
2013-12-03 13:30:00,584.0,3775.0
2013-12-03 14:00:00,309.5,3960.0
2013-12-03 14:30:00,390.5,4150.0
2013-12-03 15:00:00,240.5,4280.0
2013-12-03 15:30:00,585.0,4515.0
2013-12-03 16:00:00,279.0,4700.0
2013-12-03 16:30:00,68.85000038146973,4765.0
2013-12-03 17:00:00,2.9800000190734863,4780.0
...
(2) この csv ファイルを読み込んで pandas データフレームを作成します。
そのインデックスを元にして date カラムを追加した後のデータフレームの内容が以下です :
solar.current solar.total date
time
...
2013-12-03 07:00:00 0.120000 0.000000 2013-12-03
2013-12-03 07:30:00 59.500000 13.970000 2013-12-03
2013-12-03 08:00:00 119.500000 66.349998 2013-12-03
2013-12-03 08:30:00 571.500000 207.500000 2013-12-03
2013-12-03 09:00:00 843.000000 545.500000 2013-12-03
2013-12-03 09:30:00 689.000000 1010.000000 2013-12-03
2013-12-03 10:00:00 853.500000 1360.000000 2013-12-03
2013-12-03 10:30:00 599.500000 1745.000000 2013-12-03
2013-12-03 11:00:00 691.000000 2045.000000 2013-12-03
2013-12-03 11:30:00 684.500000 2410.000000 2013-12-03
2013-12-03 12:00:00 559.000000 2700.000000 2013-12-03
2013-12-03 12:30:00 703.500000 3010.000000 2013-12-03
2013-12-03 13:00:00 620.500000 3360.000000 2013-12-03
2013-12-03 13:30:00 584.000000 3775.000000 2013-12-03
2013-12-03 14:00:00 309.500000 3960.000000 2013-12-03
2013-12-03 14:30:00 390.500000 4150.000000 2013-12-03
2013-12-03 15:00:00 240.500000 4280.000000 2013-12-03
2013-12-03 15:30:00 585.000000 4515.000000 2013-12-03
2013-12-03 16:00:00 279.000000 4700.000000 2013-12-03
2013-12-03 16:30:00 68.849998 4765.000000 2013-12-03
2013-12-03 17:00:00 2.980000 4780.000000 2013-12-03
(3) 正規化した後のデータフレームです :
solar.current solar.total date
time
...
2013-12-03 07:00:00 0.000006 0.000000 2013-12-03
2013-12-03 07:30:00 0.002975 0.000699 2013-12-03
2013-12-03 08:00:00 0.005975 0.003317 2013-12-03
2013-12-03 08:30:00 0.028575 0.010375 2013-12-03
2013-12-03 09:00:00 0.042150 0.027275 2013-12-03
2013-12-03 09:30:00 0.034450 0.050500 2013-12-03
2013-12-03 10:00:00 0.042675 0.068000 2013-12-03
2013-12-03 10:30:00 0.029975 0.087250 2013-12-03
2013-12-03 11:00:00 0.034550 0.102250 2013-12-03
2013-12-03 11:30:00 0.034225 0.120500 2013-12-03
2013-12-03 12:00:00 0.027950 0.135000 2013-12-03
2013-12-03 12:30:00 0.035175 0.150500 2013-12-03
2013-12-03 13:00:00 0.031025 0.168000 2013-12-03
2013-12-03 13:30:00 0.029200 0.188750 2013-12-03
2013-12-03 14:00:00 0.015475 0.198000 2013-12-03
2013-12-03 14:30:00 0.019525 0.207500 2013-12-03
2013-12-03 15:00:00 0.012025 0.214000 2013-12-03
2013-12-03 15:30:00 0.029250 0.225750 2013-12-03
2013-12-03 16:00:00 0.013950 0.235000 2013-12-03
2013-12-03 16:30:00 0.003443 0.238250 2013-12-03
2013-12-03 17:00:00 0.000149 0.239000 2013-12-03
...
(4) solar.current.max と solar.total.max カラムを追加後のデータフレームです :
solar.current solar.total solar.current.max \
time
...
2013-12-03 07:00:00 0.000006 0.000000 0.042675
2013-12-03 07:30:00 0.002975 0.000699 0.042675
2013-12-03 08:00:00 0.005975 0.003317 0.042675
2013-12-03 08:30:00 0.028575 0.010375 0.042675
2013-12-03 09:00:00 0.042150 0.027275 0.042675
2013-12-03 09:30:00 0.034450 0.050500 0.042675
2013-12-03 10:00:00 0.042675 0.068000 0.042675
2013-12-03 10:30:00 0.029975 0.087250 0.042675
2013-12-03 11:00:00 0.034550 0.102250 0.042675
2013-12-03 11:30:00 0.034225 0.120500 0.042675
2013-12-03 12:00:00 0.027950 0.135000 0.042675
2013-12-03 12:30:00 0.035175 0.150500 0.042675
2013-12-03 13:00:00 0.031025 0.168000 0.042675
2013-12-03 13:30:00 0.029200 0.188750 0.042675
2013-12-03 14:00:00 0.015475 0.198000 0.042675
2013-12-03 14:30:00 0.019525 0.207500 0.042675
2013-12-03 15:00:00 0.012025 0.214000 0.042675
2013-12-03 15:30:00 0.029250 0.225750 0.042675
2013-12-03 16:00:00 0.013950 0.235000 0.042675
2013-12-03 16:30:00 0.003443 0.238250 0.042675
2013-12-03 17:00:00 0.000149 0.239000 0.042675
...
solar.total.max
time
...
2013-12-03 07:00:00 0.239
2013-12-03 07:30:00 0.239
2013-12-03 08:00:00 0.239
2013-12-03 08:30:00 0.239
2013-12-03 09:00:00 0.239
2013-12-03 09:30:00 0.239
2013-12-03 10:00:00 0.239
2013-12-03 10:30:00 0.239
2013-12-03 11:00:00 0.239
2013-12-03 11:30:00 0.239
2013-12-03 12:00:00 0.239
2013-12-03 12:30:00 0.239
2013-12-03 13:00:00 0.239
2013-12-03 13:30:00 0.239
2013-12-03 14:00:00 0.239
2013-12-03 14:30:00 0.239
2013-12-03 15:00:00 0.239
2013-12-03 15:30:00 0.239
2013-12-03 16:00:00 0.239
2013-12-03 16:30:00 0.239
2013-12-03 17:00:00 0.239
...
(5) そして最後にシークエンス化されます。solar.total をそのまま流用してシークエンスにしていることが分かります。
日毎に solar.total の最初の2個の読み取り値をベースに、14 データポイントまで要素数を順次増やしてシークエンスを作成しています :
[
array([ 0. , 0.0006985], dtype=float32),
array([ 0. , 0.0006985, 0.0033175], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 ], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 , 0.027275 ], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 , 0.027275 , 0.0505 ], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 , 0.027275 , 0.0505 , 0.068 ], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 ], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 , 0.10225 ], dtype=float32),
array([ 0. , 0.0006985, 0.0033175, 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 , 0.10225 , 0.1205 ], dtype=float32),
array([ 0. , 0.0006985 , 0.0033175 , 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 , 0.10225 , 0.1205 , 0.13500001], dtype=float32),
array([ 0. , 0.0006985 , 0.0033175 , 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 , 0.10225 , 0.1205 , 0.13500001, 0.1505 ], dtype=float32),
array([ 0. , 0.0006985 , 0.0033175 , 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 , 0.10225 , 0.1205 , 0.13500001, 0.1505 , 0.168 ], dtype=float32),
array([ 0. , 0.0006985 , 0.0033175 , 0.010375 , 0.027275 , 0.0505 , 0.068 , 0.08725 , 0.10225 , 0.1205 , 0.13500001, 0.1505 , 0.168 , 0.18875 ], dtype=float32),
...
そしてラベルには solar.total.max の値がそのまま使われています :
[[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
[ 0.23899999]
...
バッチ生成
next_batch() は訓練のための次のバッチを (python の) yield で生成していきます :
# process batches of 10 days
BATCH_SIZE = TIMESTEPS * 10
def next_batch(x, y, ds):
"""get the next batch for training"""
def as_batch(data, start, count):
return data[start:start + count]
for i in range(0, len(x[ds]), BATCH_SIZE):
yield as_batch(X[ds], i, BATCH_SIZE), as_batch(Y[ds], i, BATCH_SIZE)
5-3 モデル作成 (LSTM ネットワーク)
入力シークエンスの起こりうる最大の 14 データポイントに対応して、各データポイントのために 1 セルとして、14 LSTM セルでネットワークをモデリングします。CNTK は可変なシークエンスのサポートがありますので、LSTM への入力としてパディングのための追加の必要なしにシークエンスを as-is (そのまま) で供給できます。
(既に前節で見ていますが、) ニューラルネットワークの出力は当日のためのトータルの発電力量であり、与えられた日のための各シークエンスは同じ発電力量を持ちます。
例えば :
1.7,11.4 -> 10300
1.7,11.4,67.5 -> 10300
1.7,11.4,67.5,250.5 ... -> 10300
1.7,11.4,67.5,250.5,573.5 -> 10300
本章の LSTM モデルは次のデザインを持ちます :
ネットワークモデルは上のネットワーク図の正確な翻訳です (但し、セル数は 15 取ってあります) :
# Specify the internal-state dimensions of the LSTM cell
H_DIMS = 15
def create_model(x):
"""Create the model for time series prediction"""
with C.layers.default_options(initial_state = 0.1):
m = C.layers.Recurrence(C.layers.LSTM(H_DIMS))(x)
m = C.sequence.last(m)
m = C.layers.Dropout(0.2)(m)
m = C.layers.Dense(1)(m)
return m
セル数以外は 4 章のモデルと全く同じものです。
5-4 トレーニング
訓練を開始できる前にモデルのための入力変数をバインドしてどのオプティマイザを使用したいかを定義する必要があります。
このサンプルのために fsadagrad オプティマイザを選択します。損失関数としては squared_error を選択します。
fsadagrad は聞きなれませんが、名前から AdaGrad の亜種に思えますがコメントを見ていると Adam の亜種のようにも受け取れます。
squared_error は二乗誤差です :
# 入力シークエンス
x = C.sequence.input_variable(1)
# モデルを作成します。
z = create_model(x)
# expected output (label), also the dynamic axes of the model output
# is specified as the model of the label input
l = C.input_variable(1, dynamic_axes=z.dynamic_axes, name="y")
# 学習率
learning_rate = 0.005
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
# 損失関数
loss = C.squared_error(z, l)
# エラーの判断のためにも取り敢えず二乗誤差を使用します。
error = C.squared_error(z, l)
# fsadagrad オプティマイザを使用します。
momentum_time_constant = C.momentum_as_time_constant_schedule(BATCH_SIZE / -math.log(0.9))
learner = C.fsadagrad(z.parameters,
lr = lr_schedule,
momentum = momentum_time_constant)
trainer = C.Trainer(z, (loss, error), [learner])
| API | 説明 |
|---|---|
squared_error |
この演算は2つの入力行列ん要素間の二乗の差異の総和を計算します。 |
fsadagrad |
モデル・パラメータを学習するために FSAdaGrad learner インスタンスを作成します。 |
◆ さて訓練を実行しましょう :
# training
loss_summary = []
start = time.time()
for epoch in range(0, EPOCHS):
for x_batch, l_batch in next_batch(X, Y, "train"):
trainer.train_minibatch({x: x_batch, l: l_batch})
if epoch % (EPOCHS / 10) == 0:
training_loss = trainer.previous_minibatch_loss_average
loss_summary.append(training_loss)
print("epoch: {}, loss: {:.4f}".format(epoch, training_loss))
print("Training took {:.1f} sec".format(time.time() - start))
epoch: 0, loss: 0.1058
epoch: 10, loss: 0.0244
epoch: 20, loss: 0.0138
epoch: 30, loss: 0.0079
epoch: 40, loss: 0.0071
epoch: 50, loss: 0.0071
epoch: 60, loss: 0.0081
epoch: 70, loss: 0.0068
epoch: 80, loss: 0.0068
epoch: 90, loss: 0.0073
Training took 83.5 sec
Slow モードでも試しました :
epoch: 0, loss: 0.1058
epoch: 200, loss: 0.0070
epoch: 400, loss: 0.0079
epoch: 600, loss: 0.0079
epoch: 800, loss: 0.0079
epoch: 1000, loss: 0.0077
epoch: 1200, loss: 0.0071
epoch: 1400, loss: 0.0069
epoch: 1600, loss: 0.0072
epoch: 1800, loss: 0.0067
Training took 1627.0 sec
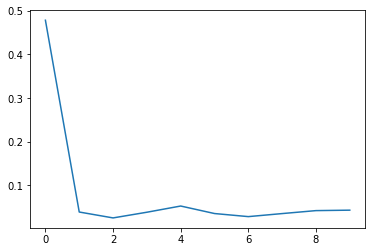
モデルの収束を損失関数のプロットで見てみます :
plt.plot(loss_summary, label='training loss');
GPU メモリ使用量
トレーニング直後に GPU メモリの使用量も確認しましたが、いずれのモードでも少量しか使用してません :
$ nvidia-smi
Sat Oct 14 14:51:11 2017
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.66 Driver Version: 384.66 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla K80 Off | 0000214E:00:00.0 Off | 0 |
| N/A 46C P0 71W / 149W | 100MiB / 11439MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 28470 C /home/masao/anaconda3/bin/python 89MiB |
+-----------------------------------------------------------------------------+
$ nvidia-smi
Sat Oct 14 15:31:42 2017
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.66 Driver Version: 384.66 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla K80 Off | 0000214E:00:00.0 Off | 0 |
| N/A 47C P0 71W / 149W | 100MiB / 11439MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 29050 C /home/masao/anaconda3/bin/python 89MiB |
+-----------------------------------------------------------------------------+
評価
訓練/検証そしてテスト・データセットで検証してみましょう。
尺度としては MSE (Mean Squared Error, 平均二乗誤差) を使用します。
単純過ぎるかもしれませんので、与えられた許容誤差の内側にどのくらいの予測があるかの比率を定義した方がより良い尺度かもしれません。
# validate
def get_mse(X,Y,labeltxt):
result = 0.0
for x1, y1 in next_batch(X, Y, labeltxt):
eval_error = trainer.test_minibatch({x : x1, l : y1})
result += eval_error
return result/len(X[labeltxt])
訓練/検証データセットの平均二乗誤差 :
# Print the train and validation errors
for labeltxt in ["train", "val"]:
print("mse for {}: {:.6f}".format(labeltxt, get_mse(X, Y, labeltxt)))
mse for train: 0.000083
mse for val: 0.000080
mse for train: 0.000043
mse for val: 0.000037
テスト・データセットの平均二乗誤差 :
# Print the test error
labeltxt = "test"
print("mse for {}: {:.6f}".format(labeltxt, get_mse(X, Y, labeltxt)))
mse for test: 0.000080
mse for test: 0.000040
当然のことながら、Slow モードの方が良い結果になっています。
5-5 結果を可視化する
結果をプロットして可視化してみましょう。
# predict
f, a = plt.subplots(2, 1, figsize=(12, 8))
for j, ds in enumerate(["val", "test"]):
results = []
for x_batch, _ in next_batch(X, Y, ds):
pred = z.eval({x: x_batch})
results.extend(pred[:, 0])
# because we normalized the input data we need to multiply the prediction
# with SCALER to get the real values.
a[j].plot((Y[ds] * NORMALIZE).flatten(), label=ds + ' raw');
a[j].plot(np.array(results) * NORMALIZE, label=ds + ' pred');
a[j].legend();
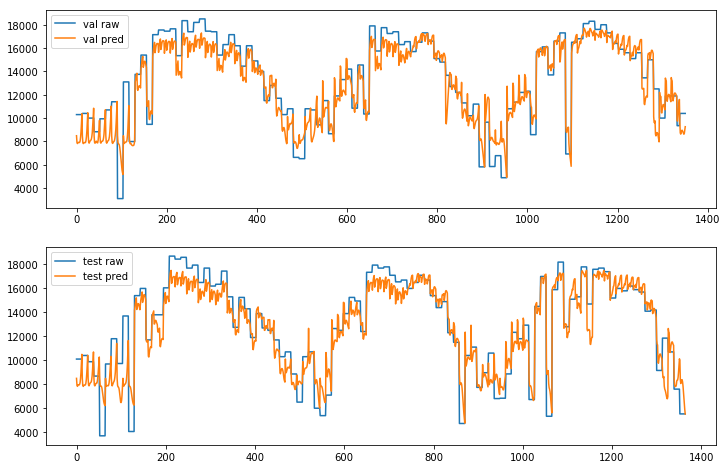
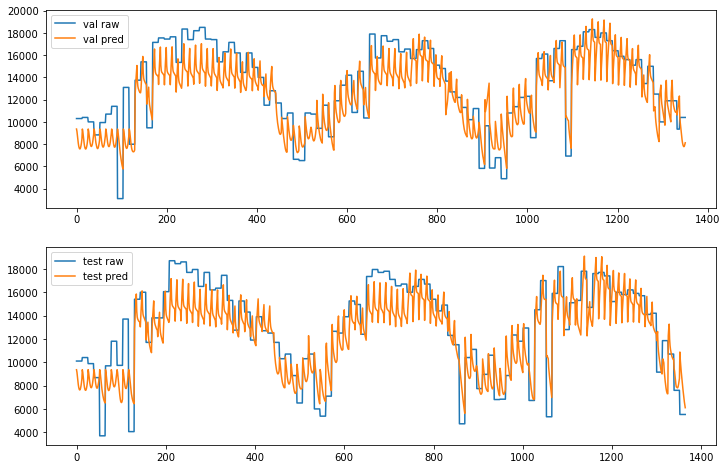
以下のグラフで青色が生データで、オレンジ色が予測を示しています :
Slow モードでは予測が実際のデータに近く正しいパターンをフォローしています :
6. What's Next
CNTK 2.2 Python API をマスターするためには CNTK 2.2 Tutorials が最適ですが、今回までの記事で以下のチュートリアル 8 編をカバーしたことになります :
- CNTK 101: Logistic Regression and ML Primer
- CNTK 102: Feed Forward Network with Simulated Data
- CNTK 103: Part A - MNIST Data Loader
- CNTK 103: Part B - Logistic Regression with MNIST
- CNTK 103: Part C - Multi Layer Perceptron with MNIST
- CNTK 103: Part D - Convolutional Neural Network with MNIST
- CNTK 106: Part A - Time series prediction with LSTM (Basics)
- CNTK 106: Part B - Time series prediction with LSTM (IOT Data)
また併せて以下のリソースもカバーしています :
従って、残りの初級チュートリアル 104, 105 に取り組むか、より上位の 200 番台に取り組んでも良いでしょう。
以上