CNTK 2.2 Python API 入門 - パッケージ構成、基本演算 & 順伝播型 NN 分類器
0. はじめに
CNTK ( Microsoft Cognitive Toolkit ) 2.2 の Python API 入門です。
CNTK は、公開当初はスマートな Caffe ツールというフレーバーのインターフェイスが基本でしたが、現在では普通に Python API が公開されています。つまり、他の深層学習フレームワークと同様に CNTK でも Python プログラムを作成することで深層学習モデルが構築できます。(書きやすいという評判のフレームワークの多くと同様に) CNTK のニューラルネットワークは Python の関数オブジェクトで表現されます。私見では、他のフレームワークよりも straightforward にコーディングできますし、ネットワーク定義もトレーニング・ループも非常に簡潔に書くことができます。
しかしながら CNTK の進化の経緯もあり、Python プログラミングに関する情報が少ないように思われますので、CNTK 2.2 Python API の入門記事を作成してみました。CNTK 2.2 Tutorials への橋渡しになることを心掛けて作成しました。
内容は :
- CNTK 2.2 Python API コンセプト
- CNTK Python パッケージ構成
- CNTK 基本演算
- 順伝播型ニューラルネットワーク分類器のコード解読
- What's Next ?
目標は CNTK Python API を利用して、下図のような分離可能なランダムデータを分類する簡単なニューラルネットワークを作成して、トレーニングそして評価することです。
入門という位置づけですので、最初に CNTK Python API のコンセプトとパッケージ構成について説明します。
そして基本演算の課題をこなしてからネットワーク構築を行ないます。この基本演算とは cntk.ops パッケージにより提供される、CNTK 計算グラフのノードとなるプリミティブです。単純なテンソル数値演算、論理演算そして活性化関数も含みます。更には入力テンソルを供給するための変数 - プレースホルダーも含んでいます。
- 特に難しいことはしていませんので、Python, NumPy 及び機械学習の基礎知識があれば十分に理解できるかと思います。
- NumPy をご存知なくても、CNTK の数値演算が element-wise であること、つまりテンソル (多次元配列) の要素に沿って計算が可能であることを理解して頂ければ十分です。
動作環境の構築が必要な場合には、Cognitive Toolkit 2.2 を Azure Linux GPU 仮想マシンにインストール を参考にしてください。Azure ポータルと Ubuntu Linux にある程度慣れていれば、30 分程度で以下のような環境が構築できるかと思います :
- Azure NC 仮想マシン with NVIDIA Tesla® K80 GPU
- Ubuntu 16.04 LTS
- NVIDIA CUDA 8.0 & cuDNN 6.0
- Anaconda 3 4.1.1
- CNTK 2.2 (for GPU)
分類器の具体的な題材としては、上記事中でも CNTK の動作確認に利用した、チュートリアルの FeedForwardNet.py を使用します。(このサンプルは Getting started でも使用されています。)
本記事を最後まで読めば (基本事項が盛り込んである、) 以下の CNTK Python プログラムが十分に理解できて実行可能になります。
import numpy as np
from cntk.device import cpu, try_set_default_device
from cntk import Trainer
from cntk.layers import Dense, Sequential, For
from cntk.learners import sgd, learning_rate_schedule, UnitType
from cntk.ops import input_variable, sigmoid
from cntk.losses import cross_entropy_with_softmax
from cntk.metrics import classification_error
from cntk.logging import ProgressPrinter
# make sure we get always the same "randomness"
np.random.seed(0)
def generate_random_data(sample_size, feature_dim, num_classes):
# Create synthetic data using NumPy.
Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes)
# Make sure that the data is separable
X = (np.random.randn(sample_size, feature_dim) + 3) * (Y + 1)
X = X.astype(np.float32)
# converting class 0 into the vector "1 0 0",
# class 1 into vector "0 1 0", ...
class_ind = [Y == class_number for class_number in range(num_classes)]
Y = np.asarray(np.hstack(class_ind), dtype=np.float32)
return X, Y
# Creates and trains a feedforward classification model
def ffnet():
input_dim = 2
num_output_classes = 2
num_hidden_layers = 2
hidden_layers_dim = 50
# Input variables denoting the features and label data
feature = input_variable((input_dim), np.float32)
label = input_variable((num_output_classes), np.float32)
netout = Sequential([For(range(num_hidden_layers), lambda i: Dense(hidden_layers_dim, activation=sigmoid)),
Dense(num_output_classes)])(feature)
ce = cross_entropy_with_softmax(netout, label)
pe = classification_error(netout, label)
lr_per_minibatch = learning_rate_schedule(0.5, UnitType.minibatch)
# Instantiate the trainer object to drive the model training
learner = sgd(netout.parameters, lr=lr_per_minibatch)
progress_printer = ProgressPrinter(128)
trainer = Trainer(netout, (ce, pe), learner, progress_printer)
# Get minibatches of training data and perform model training
minibatch_size = 25
for i in range(1024):
features, labels = generate_random_data(
minibatch_size, input_dim, num_output_classes)
# Specify the mapping of input variables in the model to actual
# minibatch data to be trained with
trainer.train_minibatch({feature: features, label: labels})
trainer.summarize_training_progress()
test_features, test_labels = generate_random_data(
minibatch_size, input_dim, num_output_classes)
avg_error = trainer.test_minibatch(
{feature: test_features, label: test_labels})
return avg_error
if __name__ == '__main__':
# Specify the target device to be used for computing, if you do not want to
# use the best available one, e.g.
# try_set_default_device(cpu())
error = ffnet()
print(" error rate on an unseen minibatch %f" % error)
1. CNTK 2.2 Python API コンセプト
最初に CNTK 2.2 Python API のコンセプトを知るために CNTK Library API の説明を見ておきます (以下の引用は翻訳です) :
CNTK Python API は、モデル定義と計算、学習アルゴリズム、データ・リーディングと分散訓練のための抽象モジュールから構成されます。
- 柔軟性と簡潔性 : これらの抽象モジュールはあらゆるニューラルネットワークの定義と訓練において、柔軟性と簡潔さの両者を直交性 (独立性) が高く提供するための基礎となります。
- 効率的なデータ・インターフェイス : 単純ですがしかし軽量のデータ・インターフェイスはネイティブな numpy 配列の形式のデータを計算エンジンに効率的に供給することを可能にします。
-
組み込みデータ・リーダー: 画像、テキスト・フォーマットと音声 HTK (Hidden markov model ToolKit, 隠れマルコフモデル・ツールキット) データフォーマットのための、CNTK 組み込みである最適化されスケーラブルなデータ・リーダーもまた Python
API から利用可能です。これはユーザがデータを読むためのコードを作成することなしに既存のデータで直接トレーニングすることを容易にします。 - 高度にスケーラブルな学習 : API は高度にスケーラブルなトレーニング性能を公開しています (1-Bit SGD のような並列アルゴリズム)。分散トレーニング・サンプル はトレーニング並列 API を示します。
- 簡潔なネットワーク定義 : API は、CNTK V1 に類似した再起性 (= recurrence) を含む簡潔で高度なニューラルネットワーク定義を可能にする高位な 層ライブラリ を含みます。ツールキットは、再起ステップの静的展開を要求する代わりにネットワークにおける循環としてのシンボリック・フォームのリカレント・モデルの表現をサポートします。より一般的には、これはリカレント・ニューラルネットワークの簡潔で効率的な表現と実行という結果になります。
CNTK Python API の総てのコア計算、学習、そしてデータ・リーディング API 抽象モジュールは Python と C++ の両者から非常に簡単に拡張可能で、新しい演算子、学習主体 (= learner) そしてデータ・リーダーを簡単に実装することを可能にします、これはライブラリの組み込み機能で自由に構成できます。
API は新しい プロトコルバッファ ベースのモデル・シリアライゼーションを導入します、これはセーブされたモデルの後方そして前方互換性をサポートします。
データ・インターフェイスを NumPy ベースにしたのは賢明な判断と言えましょう。あくまで私的見解ですが、期待したい点として以下をあげておきます :
- 深層学習フレームワークを利用する場合、データを読み込んで供給するまでのコーディングに時間が割かれるケースが多々ありますが、かなりの改善が期待できそうです。
- ネットワーク定義の簡潔さ。この性質は今回扱うサンプルでも見て取れますが、特にリカレント・ニューラルネットワークの定義に期待しましょう。
- スケーラブルな分散トレーニング。分散トレーニングについては、今のところ他のフレームワークでは柔軟性の欠如・実装の難しさなどの点から決め手に欠けていると考えていますので、CNTK には大いに期待したいところです。
次に、プログラマ視点からもう少し具体的に見ていきましょう。
2. CNTK Python パッケージ構成
Python ライブラリとして site-packages/cntk にインストールされた CNTK ライブラリのパッケージ構成を確認します :
$ ls -F
axis.py debugging/ __init__.py libs/ ops/ tensor.py
cntk_py.py default_options.py internal/ logging/ __pycache__/ tests/
conftest.py device.py io/ losses/ pytest.ini train/
contrib/ eval/ layers/ metrics/ random/ variables.py
core.py initializer.py learners/ misc/ sample_installer.py
ライブラリ構成は標準的な深層学習フレームワークの構成と言って良いでしょう。
なお、learners は学習アルゴリズムを実装したオプティマイザーと考えて良いです。
次に、サブモジュールとサブパッケージについて Python API リファレンス - cntk パッケージ を参照して、提供される機能を確認してみましょう。これらは冒頭に示したサンプル・プログラムでもインポートされて利用されています。
2-1 cntk サブパッケージ
| パッケージ名 | 提供される機能 |
|---|---|
| cntk.contrib | CNTK のための特別なユティリティ、例えば、他の深層学習ツールキットへの橋渡しをするユティリティ。 |
| cntk.debugging | cntk.debugging.debug, cntk.debugging.profiler |
| cntk.eval | モデル評価のためのユティリティ。 |
| cntk.io | CNTK I/O ユティリティ。 |
| cntk.layers | CNTK 層ライブラリ。 |
| cntk.learners | learner はトレーニング・プロセスの間パラメータ・セットの調整をします。パラメータの異なるセットのために異なる learner を使用できます。現在、CNTK は次の学習アルゴリズムをサポートしています : AdaDelta, AdaGrad, FSAdaGrad, Adam, MomentumSGD, Nesterov, RMSProp, SGD |
| cntk.logging | ロギングのためのユティリティ。 |
| cntk.losses | 損失関数。 |
| cntk.metrics | 評価メトリクス。 |
| cntk.misc | CNTK のための様々なユティリティ、例えば、CNTK 計算グラフのノードをフィルタリングして変換します。 |
| cntk.ops | CNTK コア演算子。これらの演算子の呼び出しは CNTK 計算グラフのノードを作成します。 |
| cntk.random | 指定された分布に関する乱数を生成する関数。 |
| cntk.train | トレーニングのためのユティリティ。 |
2-2 cntk サブモジュール
| モジュール名 | 提供される機能 |
|---|---|
| cntk.axis | データ・バインディングにおける CNTK 変数のための Axis(軸)。 |
| cntk.core | コア数値構築、NDArrayView, View クラス。 |
| cntk.default_options | CNTK 関数のデフォルト・オプション。 |
| cntk.device | CNTK 計算がその上で実行されるデバイスを指定するユティリティ。 |
| cntk.initializer | パラメータの初期化子。 |
| cntk.sample_installer | CNTK サンプルデータを取得するためのユティリティ。 |
| cntk.tensor | テンソル演算。 |
| cntk.variables | CNTK 変数、パラメータ、定数、そしてレコード。 |
3. CNTK 基本演算
ここから具体的なオペレーションを行ないます。CNTK に慣れるために、cntk.ops パッケージの演算子を各種試してみます。
最初に重要なノードであるプレースホルダーにふれた後で、簡単な数値演算・論理演算を実行していきます。
※ 冒頭でも言及しましたが、動作環境の構築の構築が必要な場合には Cognitive Toolkit 2.2 を Azure Linux GPU 仮想マシンにインストール を参考にしてください。
Python インタープリタを起動したら、準備として最初に numpy と cntk を import して CNTK のバージョンの確認をしておきましょう :
>>> import numpy as np
>>> import cntk as C
>>> C.__version__
'2.2'
これらの演算子は総て CNTK 計算グラフのノードと考えて良いです。共通の eval() メソッドは、そのノードのために forward パス (順伝播計算) を実行した時に呼び出し可能で forward パスの結果を返します。
NumPy の基礎知識があれば理解しやすいですが、そうでない場合でも以下を抑えておけば問題ありません :
- 演算の多くは element-wise です、つまり配列の要素ごと、あるいは要素に渡る計算が可能です。
- 説明文に出てくる「ブロードキャスト」は、大雑把に言えば、複数の入力配列の ndim/shape (次元/形状) がミスマッチな場合でも ndim/shape を自動調節した上で計算してくれる便利な機能です。
3-1 プレースホルダー
cntk.ops.input_variable() はネットワークの入力を作成する、モデル作成に必須のノードで、特徴やラベルのようなデータをモデルに供給するために使用されます。CNTK のドキュメントではプレースホルダーという呼称は使用していませんが、いわゆるプレースホルダーと同義と考えて良いです。
>>> x = C.input_variable(2)
>>> y = C.input_variable(2)
>>> x0 = np.asarray([[2., 1.]], dtype=np.float32)
>>> y0 = np.asarray([[4., 6.]], dtype=np.float32)
>>> C.squared_error(x, y).eval({x:x0, y:y0})
Selected GPU[0] Tesla K80 as the process wide default device.
array([ 29.], dtype=float32)
この例では、最初に2つの入力変数 x, y を shape(1,2) で設定しています。
そしてこれら2つの変数を入力として squared_error (二乗誤差) ノードを作成しています。
squared_error の eval メソッドの内側ではこれら2つの変数のためにデータの入力マッピングが設定できます。
この例では2つの NumPy 配列を渡していて、二乗誤差は (2-4)**2 + (1-6)**2 = 29 となります。
3-2 定数定義
cntk.ops.constant() は NumPy 配列から定数テンソルを作成します。
>>> constant_data = C.constant([[1., 2.], [3., 4.], [5., 6.]])
Selected GPU[0] Tesla K80 as the process wide default device.
>>> constant_data.value
array([[ 1., 2.],
[ 3., 4.],
[ 5., 6.]], dtype=float32)
>>> constant_data.asarray()
array([[ 1., 2.],
[ 3., 4.],
[ 5., 6.]], dtype=float32)
パラメータ、定数、値、etc. のようなデータ・コンテナの多くは asarray() メソッドを実装していて、これらは NumPy インターフェイスを返します。
>>> c = C.constant(3, shape=(2,3))
Selected GPU[0] Tesla K80 as the process wide default device.
>>> c.asarray()
array([[ 3., 3., 3.],
[ 3., 3., 3.]], dtype=float32)
>>> np.ones_like(c.asarray())
array([[ 1., 1., 1.],
[ 1., 1., 1.]], dtype=float32)
3-3 簡単な数値演算
次に、cntk.ops の数値演算ノードを列挙していきます。最初は数値演算の中でも簡単なものをあげていきます。
※ 以後、出力文字列 "Selected GPU[0] Tesla K80 as the process wide default device." は省略します。
abs - 要素ごとに絶対値を計算します :
>>> C.abs([-1, 1, -2, 3]).eval()
array([ 1., 1., 2., 3.], dtype=float32)
ceil - いわゆる天井関数で、入力値以上の最小の整数を要素ごとに計算します。
>>> C.ceil([0.2, 1.3, 4., 5.5, 0.0]).eval()
array([ 1., 2., 4., 6., 0.], dtype=float32)
>>> C.ceil([[0.6, 3.3], [1.9, 5.6]]).eval()
array([[ 1., 4.],
[ 2., 6.]], dtype=float32)
cos - 要素ごとに三角関数の cosine (コサイン) を計算します。
np.round(C.cos(np.arccos([[1,0.5],[-0.25,-0.75]])).eval(),5)
array([[ 1. , 0.5 ],
[-0.25, -0.75]], dtype=float32)
exp - 要素ごとに指数を計算します。
>>> C.exp([0., 1.]).eval()
array([ 1. , 2.71828175], dtype=float32)
floor - いわゆる床関数で、入力値以下の最大の整数を要素ごとに計算します。
>>> C.floor([0.2, 1.3, 4., 5.5, 0.0]).eval()
array([ 0., 1., 4., 5., 0.], dtype=float32)
>>> C.floor([[0.6, 3.3], [1.9, 5.6]]).eval()
array([[ 0., 3.],
[ 1., 5.]], dtype=float32)
>>> C.floor([-5.5, -4.2, -3., -0.7, 0]).eval()
array([-6., -5., -3., -1., 0.], dtype=float32)
>>> C.floor([[-0.6, -4.3], [1.9, -3.2]]).eval()
array([[-1., -5.],
[ 1., -4.]], dtype=float32)
log - 要素ごとに対数を計算します。
>>> C.log([1., 2.]).eval()
array([ 0. , 0.69314718], dtype=float32)
minus - 減算です。ブロードキャストもサポートしています。
※ ブロードキャストは、複数の入力配列の ndim/shape (次元/形状) がミスマッチな場合でも、ndim/shape を自動調節した上で計算してくれる機能です。
>>> C.minus([1, 2, 3], [4, 5, 6]).eval()
array([-3., -3., -3.], dtype=float32)
>>> C.minus([[1,2],[3,4]], 1).eval()
array([[ 0., 1.],
[ 2., 3.]], dtype=float32)
negate - 要素ごとの negation (否定、符号反転) を計算します。
>>> C.negate([-1, 1, -2, 3]).eval()
array([ 1., -1., 2., -3.], dtype=float32)
plus - 加算。ブロードキャストもサポートしています。
>>> C.plus([1, 2, 3], [4, 5, 6]).eval()
array([ 5., 7., 9.], dtype=float32)
>>> C.plus([-5, -4, -3, -2, -1], [10]).eval()
array([ 5., 6., 7., 8., 9.], dtype=float32)
>>> C.plus([-5, -4, -3, -2, -1], [10], [3, 2, 3, 2, 3], [-13], [+42], 'multi_arg_example').eval()
array([ 37., 37., 39., 39., 41.], dtype=float32)
>>> C.plus([-5, -4, -3, -2, -1], [10], [3, 2, 3, 2, 3]).eval()
array([ 8., 8., 10., 10., 12.], dtype=float32)
reciprocal - 要素ごとの逆数を計算します。
>>> C.reciprocal([-1/3, 1/5, -2, 3]).eval()
array([-3. , 5. , -0.5 , 0.33333334], dtype=float32)
sin - 要素ごとに三角関数の sin (サイン) を計算します。
>>> np.round(C.sin(np.arcsin([[1,0.5],[-0.25,-0.75]])).eval(),5)
Selected CPU as the process wide default device.
array([[ 1. , 0.5 ],
[-0.25, -0.75]], dtype=float32)
3-4 論理演算
次に基本的な論理演算です。これも簡単でしょう。
equal - 2つのテンソルの要素ごとの比較です。値が同じ場合には 1 を返し、そうでない場合には 0 を返します。
>>> C.equal([41., 42., 43.], [42., 42., 42.]).eval()
array([ 0., 1., 0.], dtype=float32)
>>> C.equal([-1,0,1], [1]).eval()
array([ 0., 0., 1.], dtype=float32)
greater(left, right) - 2つのテンソルの要素ごとの比較です。left > right の場合には 1 を返し、そうでない場合には 0 を返します。
>>> C.greater([41., 42., 43.], [42., 42., 42.]).eval()
array([ 0., 0., 1.], dtype=float32)
>>> C.greater([-1,0,1], [0]).eval()
array([ 0., 0., 1.], dtype=float32)
greater_equal(left, right) - 2つのテンソルの要素ごとの比較です。left >= right の場合には 1 を返し、そうでない場合には 0 を返します。
>>> C.greater_equal([41., 42., 43.], [42., 42., 42.]).eval()
array([ 0., 1., 1.], dtype=float32)
>>> C.greater_equal([-1,0,1], [0]).eval()
array([ 0., 1., 1.], dtype=float32)
less(left, right) - 2つのテンソルの要素ごとの比較です。left < right の場合には 1 を返し、そうでない場合には 0 を返します。
>>> C.less([41., 42., 43.], [42., 42., 42.]).eval()
array([ 1., 0., 0.], dtype=float32)
>>> C.less([-1,0,1], [0]).eval()
array([ 1., 0., 0.], dtype=float32)
less_equal(left, right) - 2つのテンソルの要素ごとの比較です。left <= right の場合には 1 を返し、そうでない場合には 0 を返します。
>>> C.less_equal([41., 42., 43.], [42., 42., 42.]).eval()
array([ 1., 1., 0.], dtype=float32)
>>> C.less_equal([-1,0,1], [0]).eval()
array([ 1., 1., 0.], dtype=float32)
not_equal - 2つのテンソルの要素ごとの比較です。left != right の場合には 1 を返し、そうでない場合には 0 を返します。
>>> C.not_equal([41., 42., 43.], [42., 42., 42.]).eval()
array([ 1., 0., 1.], dtype=float32)
>>> C.not_equal([-1,0,1], [0]).eval()
array([ 1., 0., 1.], dtype=float32)
3-5 少し高度な数値演算
これらは参考までにあげておきます。機械学習では argmax, argmin は良く使います。
acos - 要素ごとに arccos を計算します。arccos (逆余弦) は cos の逆関数です。
>>> np.round(C.acos([[1,0.5],[-0.25,-0.75]]).eval(),5)
array([[ 0. , 1.04719996],
[ 1.82348001, 2.41885996]], dtype=float32)
argmax(x, axis=None) - 指定された軸に沿って要素の argmax を計算します (インデックスを返す点に注意してください)。
>>> data = [[10, 20],[30, 40],[50, 60]]
>>> C.argmax(data, 0).eval()
array([[ 2., 2.]], dtype=float32)
>>> C.argmax(data, 1).eval()
array([[ 1.],
[ 1.],
[ 1.]], dtype=float32)
argmin(x, axis=None) - 指定された軸に沿って要素の argmin を計算します。
>>> data = [[10, 30],[40, 20],[60, 50]]
>>> C.argmin(data, 0).eval()
array([[ 0., 1.]], dtype=float32)
>>> C.argmin(data, 1).eval()
array([[ 0.],
[ 1.],
[ 1.]], dtype=float32)
asin - 要素ごとに arcsin を計算します。arcsin (逆正弦) は sin の逆関数です。
>>> np.round(C.asin([[1,0.5],[-0.25,-0.75]]).eval(),5)
array([[ 1.57079995, 0.52359998],
[-0.25268 , -0.84806001]], dtype=float32)
clip(x, min_value, max_value) - min_value と max_value の間に収まるようにクリップします。
>>> C.clip([1., 2.1, 3.0, 4.1], 2., 4.).eval()
array([ 2. , 2.0999999, 3. , 4. ], dtype=float32)
>>> C.clip([-10., -5., 0., 5., 10.], [-5., -4., 0., 3., 5.], [5., 4., 1., 4., 9.]).eval()
array([-5., -4., 0., 4., 9.], dtype=float32)
cosh - 要素ごとに cosh (hyperbolic cosine, 双曲線余弦関数) を計算します。
>>> np.round(C.cosh([[1,0.5],[-0.25,-0.75]]).eval(),5)
array([[ 1.54307997, 1.12763 ],
[ 1.03140998, 1.29468 ]], dtype=float32)
element_divide - 2つの入力に対して要素ごとの除算を行ないます。ブロードキャストもサポートしています。
>>> C.element_divide([1., 1., 1., 1.], [0.5, 0.25, 0.125, 0.]).eval()
array([ 2., 4., 8., 0.], dtype=float32)
>>> C.element_divide([5., 10., 15., 30.], [2.]).eval()
array([ 2.5, 5. , 7.5, 15. ], dtype=float32)
element_max - 2つまたはそれ以上のテンソルの要素ごとの max を計算します。ブロードキャストもサポートしています。
>>> C.element_max([1., 1., 1., 1.], [0.5, 0.25, 0.125, 0.]).eval()
array([ 1., 1., 1., 1.], dtype=float32)
>>> C.element_max([1., 2., 3., 4., 5., 6., 7. ,8.], 4).eval()
array([ 4., 4., 4., 4., 5., 6., 7., 8.], dtype=float32)
element_min - 2つまたはそれ以上のテンソルの要素ごとの min を計算します。ブロードキャストもサポートしています。
>>> C.element_min([1., 1., 1., 1.], [0.5, 0.25, 0.125, 0.]).eval()
array([ 0.5 , 0.25 , 0.125, 0. ], dtype=float32)
>>> C.element_min([1., 2., 3., 4., 5., 6., 7. ,8.], 4).eval()
array([ 1., 2., 3., 4., 4., 4., 4., 4.], dtype=float32)
element_times - 2つまたはそれ以上のテンソルの要素ごとの積を計算します。ブロードキャストもサポートしています。
>>> C.element_times([1., 1., 1., 1.], [0.5, 0.25, 0.125, 0.]).eval()
array([ 0.5 , 0.25 , 0.125, 0. ], dtype=float32)
>>> C.element_times([5., 10., 15., 30.], [2.]).eval()
array([ 10., 20., 30., 60.], dtype=float32)
>>> C.element_times([5., 10., 15., 30.], [2.], [1., 2., 1., 2.]).eval()
array([ 10., 40., 30., 120.], dtype=float32)
log_add_exp - 2つまたはそれ以上の入力テンソルの指数の和の対数を計算します。
>>> a = np.arange(3,dtype=np.float32)
>>> np.exp(C.log_add_exp(np.log(1+a), np.log(1+a*a)).eval())
array([ 2., 4., 8.], dtype=float32)
>>> np.exp(C.log_add_exp(np.log(1+a), [0.]).eval())
array([ 2., 3., 4.], dtype=float32)
pow(base, exponent) - べき乗。base (底) を exponent (指数) でべき乗します。ブロードキャストもサポートしています。
>>> C.pow([1, 2, -2], [3, -2, 3]).eval()
array([ 1. , 0.25, -8. ], dtype=float32)
>>> C.pow([[0.5, 2],[4, 1]], -2).eval()
array([[ 4. , 0.25 ],
[ 0.0625, 1. ]], dtype=float32)
reduce_log_sum_exp(x, axis=None) - 指定された軸に渡り入力テンソルの要素の指数の総和の log を計算します。
>>> data = np.array([[[5,1], [20,2]],[[30,1], [40,2]],[[55,1], [60,2]]], dtype=np.float32)
>>> C.reduce_log_sum_exp(data, axis=0).eval().round(4)
array([[[ 55. , 2.09859991],
[ 60. , 3.09859991]]], dtype=float32)
>>> np.log(np.sum(np.exp(data), axis=0)).round(4)
array([[ 55. , 2.09859991],
[ 60. , 3.09859991]], dtype=float32)
3-6. その他
次章でも使用しますが、活性化関数 (sigmoid, tanh, relu, leaky_relu 等)、更には dropout も cntk.ops パッケージに含まれています。
4. 順伝播型ニューラルネットワーク分類器のコード解読
さて、基礎知識は得られましたので本記事の目的である、冒頭に掲載したサンプル・プログラムを解読して実行してみましょう。
題材とするサンプル・プログラムは FeedForwardNet.py です。
"python -m cntk.sample_installer" でサンプルをインストールした場合には、ディレクトリ "~/CNTK-Samples-2-2/Tutorials/NumpyInterop/" 下に配備されます。
サンプルの内容を簡単に説明しておくと、NumPy で生成したランダムな合成データ (2 次元特徴データとラベル) を訓練/テスト・データとして、隠れ層2つを持つ順伝播型ニューラルネットワーク分類器をトレーニングして評価します。
4-1 コード解説
デバイス設定
サンプルでは該当コードがコメントアウトされていますが、最初にデバイス設定についてふれておきます。
CNTK でネットワークを訓練し実行するにあたり、どのデバイス上でそれが実行されるべきかを決定することができます。
言うまでもなく GPU へアクセスできれば訓練時間は大幅に短縮されます。
明示的にデバイスを GPU に設定するには、cntk.device.try_set_default_device() 関数を使用して次のようにしてターゲットデバイスを設定します :
>>> from cntk.device import try_set_default_device, gpu
>>> try_set_default_device(gpu(0))
True
因みに、CPU-only 環境で GPU デバイスの設定にいくと、"Specified GPU device id (0) is invalid." というエラーになります :
>>> from cntk.device import try_set_default_device, gpu
>>> try_set_default_device(gpu(0))
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "/home/masao/anaconda3/lib/python3.6/site-packages/cntk/internal/swig_helper.py", line 69, in wrapper
result = f(*args, **kwds)
File "/home/masao/anaconda3/lib/python3.6/site-packages/cntk/device.py", line 96, in gpu
return cntk_py.DeviceDescriptor.gpu_device(device_id)
ValueError: Specified GPU device id (0) is invalid.
[CALL STACK]
...
インポート
さて、それではサンプルのコードを具体的に見ていきましょう。まずは cntk のサブモジュールやサブパッケージを numpy とともに import します。もちろん、"2. CNTK Python パッケージ構成" でまとめたものが利用されています。
import numpy as np
from cntk.device import cpu, try_set_default_device
from cntk import Trainer
from cntk.layers import Dense, Sequential, For
from cntk.learners import sgd, learning_rate_schedule, UnitType
from cntk.ops import input_variable, sigmoid
from cntk.losses import cross_entropy_with_softmax
from cntk.metrics import classification_error
from cntk.logging import ProgressPrinter
データ生成
generate_random_data 関数は numpy を利用して分離可能なランダムデータ - 2 次元特徴ベクトル X とラベル Y を生成します。合成データとは言え、ラベルから特徴を生成するという不自然なことをしているために少し分かりにくくなっていますので、詳しく説明しておきます。
def generate_random_data(sample_size, feature_dim, num_classes):
# NumPy を使用して合成データを作成する。
Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes)
# データが分離可能であることを確かなものとする
X = (np.random.randn(sample_size, feature_dim) + 3) * (Y + 1)
X = X.astype(np.float32)
# クラス 0 をベクトル "1 0 0 " に変換し、
# クラス 1 はベクトル "0 1 0" へ, ...
class_ind = [Y == class_number for class_number in range(num_classes)]
Y = np.asarray(np.hstack(class_ind), dtype=np.float32)
return X, Y
具体的な生成手順としては :
(1) まず二値の shape (25,1) のラベル Y を生成します。一回目に生成されたラベル Y を出力すると以下のようになっています :
[[0] [1] [1] [0] [1] [1] [1] [1] [1] [1] [1] [0] [0] [1] [0] [0] [0] [0] [0] [1] [0] [1] [1] [0] [0]]
(2) 相関関係を持たせるために Y を算入して shape (25, 2) の特徴ベクトル X を生成します。一回目に生成される特徴 X は以下のようなものです :
[[ 4.12531424 2.64100456] [ 8.44121647 3.32100892] [ 6.85674667 5.75307369] [ 4.41437721 2.87594938] [ 10.01631451 6.45977306]
[ 7.20978737 9.25431919] [ 9.18912125 6.46086836] [ 5.87017918 4.06203938] [ 7.18248558 4.4344492 ] [ 5.11153412 5.30962753]
[ 4.2363987 5.11469364] [ 2.4590838 1.67677259] [ 2.88720107 3.90734601] [ 7.63053989 6.45819569] [ 1.97382116 3.47752547]
[ 4.29269838 2.26854181] [ 1.39459777 3.9894762 ] [ 3.11081457 2.61906862] [ 3.11495924 3.3453126 ] [ 2.53008246 9.31670189]
[ 5.29977131 2.52886462] [ 8.52543068 3.65896916] [ 8.13157845 4.60012531] [ 3.14407921 3.39854217] [ 3.0268693 4.05583715]]
(3) 訓練 (そして評価) 用にラベル Y を one-hot ベクトルに変換します。
※ one-hot ベクトルは一つの要素だけが 1 で他の要素が 0 のベクトルです。扱いやすさのために機械学習では良くこの表現が使用されます。
※ このケースは 2 次元であるために分かりにくいですが、(1) のデータ表現と一つずつ比較すれば何をしているか理解しやすいと思います。
[[ 1. 0.] [ 0. 1.] [ 0. 1.] [ 1. 0.] [ 0. 1.] [ 0. 1.] [ 0. 1.] [ 0. 1.] [ 0. 1.] [ 0. 1.]
[ 0. 1.] [ 1. 0.] [ 1. 0.] [ 0. 1.] [ 1. 0.] [ 1. 0.] [ 1. 0.] [ 1. 0.] [ 1. 0.] [ 0. 1.]
[ 1. 0.] [ 0. 1.] [ 0. 1.] [ 1. 0.] [ 1. 0.]]
(4) そして呼び出し側に X, Y を返します。
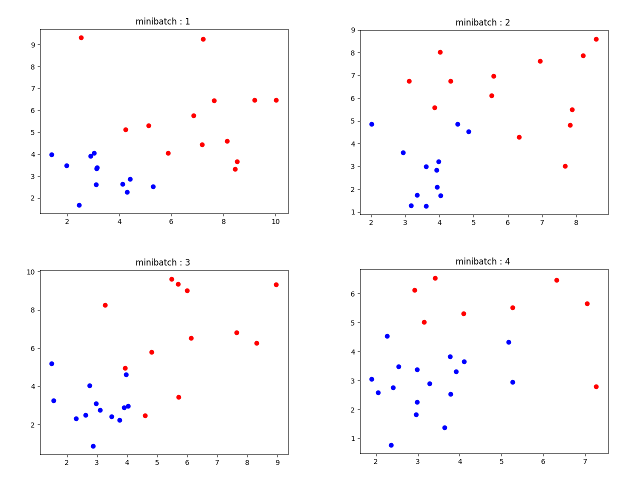
【補足】
直感的に分かりやすくするために、matplotlib を使用して生成されたデータを可視化してみました。
ラベル 0 を青色・ラベル 1 を赤色として、1 回目から 4 回めまでのミニバッチ生成データを可視化すると、以下のようになります。
もちろん分離可能で、従って分類可能です :
プレースホルダー
プレースホルダーについては "3-1 プレースホルダー" で説明しましたが、入力変数 feature と label を作成しています。
トレーニング・ループでこれらにミニバッチとしてデータが供給されることによって、モデル・パラメータの最適化が進んでいくことになります。2つの入力変数 feature, label はいずれも shape(1,2) で設定されています。label に供給されるデータは one-hot ベクトル表現に変換されていることに注意しましょう。
input_dim = 2
num_output_classes = 2
...
# 特徴とラベルデータを示す入力変数
feature = input_variable((input_dim), np.float32)
label = input_variable((num_output_classes), np.float32)
ネットワーク定義
CNTK のネットワーク定義は、冒頭でも言及しましたが Python 関数オブジェクトとして実装されます。
Python ライクな記法も使用されていて驚くほど簡潔です :
num_hidden_layers = 2
hidden_layers_dim = 50
...
netout = Sequential([For(range(num_hidden_layers), lambda i: Dense(hidden_layers_dim, activation=sigmoid)),
Dense(num_output_classes)])(feature)
このままでも十分に直感的に分かりやすいのですが、念のために仕様を確認しておくと :
- Sequential は層のリストを引数に取る、層ファクトリです。
- For (cntk.layers.For) は python の "for" に類似した層ファクトリ関数です。lambda 記法が利用できます。
- Dense は完全結合層のインスタンスを作成するための層ファクトリ関数です。
つまり、全体として次のような構造を持つ順伝播 (feedforward) ニューラルネットワークが定義されていることになります :
- 入力 (層) は特徴ベクトルのミニバッチである feature を受け取る
- 隠れ層 1 : 50 ユニットを持つ完全結合層 (活性化関数 : sigmoid)
- 隠れ層 2 : 50 ユニットを持つ完全結合層 (活性化関数 : sigmoid)
- 出力層 (分類層) : 分類クラス数 2 のための完全結合層
損失関数・評価メトリクス
損失関数としては定石どおり cross_entropy_with_softmax() が使用されています。
この関数は入力に対して Softmax を適用した上で交差エントロピーを計算しています。
大雑把に言えば、確率分布に直した上でネットワーク出力とラベルの差異をエントロピーという乱雑さを表わす尺度を利用して計算しています。
ce = cross_entropy_with_softmax(netout, label)
pe = classification_error(netout, label)
classification_error() の方は分類エラーを計算する評価メトリクスです。
評価メトリクスは必須なものではなく、また微分可能でなくても良いです。Trainer オブジェクトに渡すことによってモデルのクオリティを分かりやすい表現で追跡できます。
learner
learner は最初はオプティマイザーと考えれば分かりやすいのですが、学習の主体くらいの意味でしょう。
cntk.learners.sgd はもちろん学習アルゴリズムとして SGD が実装されていて
引数としてはネットワーク・パラメータのリストと learning_rate_schedule オブジェクトを取ります。
cntk.learners パッケージには他にも cntk.learners.adadelta, adagrad, adam, momentum_sgd, rmsprop などが実装されています。なお、Adamax は adam のオプションで指定可能です。
lr_per_minibatch = learning_rate_schedule(0.5, UnitType.minibatch)
# Instantiate the trainer object to drive the model training
learner = sgd(netout.parameters, lr=lr_per_minibatch)
ProgressPrinter
トレーニング/評価の進捗を示すユティリティで、(損失やメトリクスのような) 様々な統計情報を出力することを可能にします。
引数の数字はミニバッチ数をベースとした表示頻度です。
progress_printer = ProgressPrinter(128)
Trainer
与えられたモデル・パラメータを、指定された損失関数を使用してトレーニングするためのクラスです。
モデル・パラメータの更新のためには、先に cntk.learners.sgd オブジェクトとして作成された learner が使用されます。
オプションでメトリクス関数を指定すれば訓練されたモデルのクオリティを追跡できます。
trainer = Trainer(netout, (ce, pe), learner, progress_printer)
トレーニング・ループ
Trainer オブジェクトを使用したトレーニング・ループは非常に簡潔です。
各種フレームワークの中でもこのトレーニング・ループは最も簡潔なものの一つと言えるでしょう。
ミニバッチを生成するたびに Trainer オブジェクトの train_minibatch メソッドに渡してやれば、モデル・パラメータが最適化されていきます。
for i in range(1024):
features, labels = generate_random_data(
minibatch_size, input_dim, num_output_classes)
# Specify the mapping of input variables in the model to actual
# minibatch data to be trained with
trainer.train_minibatch({feature: features, label: labels})
評価
評価のためには、Trainer オブジェクトの test_minibatch メソッドを使用してください。
trainer.summarize_training_progress()
test_features, test_labels = generate_random_data(
minibatch_size, input_dim, num_output_classes)
avg_error = trainer.test_minibatch(
{feature: test_features, label: test_labels})
4-2 まとめと実行
以上で、冒頭のサンプル・スクリプトの解読は完了です。
CNTK Python API では、モデル作成からトレーニングへの流れが非常に分かりやすいです。
復習も兼ねて、深層学習モデルのトレーニングにフォーカスして主要なコード・ピースだけをまとめて流れを追ってみると、以下のようになります :
# 特徴とラベルのためのプレースホルダーの作成
feature = input_variable((input_dim), np.float32)
label = input_variable((num_output_classes), np.float32)
# 順伝播ニューラルネットワークの定義
netout = Sequential([For(range(num_hidden_layers), lambda i: Dense(hidden_layers_dim, activation=sigmoid)),
Dense(num_output_classes)])(feature)
# 損失関数の指定
ce = cross_entropy_with_softmax(netout, label)
# 学習アルゴリズムの指定
learner = sgd(netout.parameters, lr=lr_per_minibatch)
# Trainer オブジェクトの作成
trainer = Trainer(netout, (ce, pe), learner, progress_printer)
# 訓練ループ
for i in range(1024):
# ミニバッチの作成
features, labels = generate_random_data(minibatch_size, input_dim, num_output_classes)
# ミニバッチ・データを供給してモデル・パラメータを調整
trainer.train_minibatch({feature: features, label: labels})
最後に、GPU 環境でサンプル・スクリプトを実行しておきましょう :
$ python FeedForwardNet.py
Selected GPU[0] Tesla K80 as the process wide default device.
-------------------------------------------------------------------
Build info:
Built time: Sep 15 2017 07:30:54
Last modified date: Fri Sep 15 04:28:48 2017
Build type: release
Build target: GPU
With 1bit-SGD: no
With ASGD: yes
Math lib: mkl
CUDA version: 9.0.0
CUDNN version: 6.0.21
Build Branch: HEAD
Build SHA1: 23878e5d1f73180d6564b6f907b14fe5f53513bb
MPI distribution: Open MPI
MPI version: 1.10.7
-------------------------------------------------------------------
Learning rate per minibatch: 0.5
Minibatch[ 1- 128]: loss = 0.614628 * 3200, metric = 29.25% * 3200;
Minibatch[ 129- 256]: loss = 0.332382 * 3200, metric = 13.31% * 3200;
Minibatch[ 257- 384]: loss = 0.298804 * 3200, metric = 11.59% * 3200;
Minibatch[ 385- 512]: loss = 0.271270 * 3200, metric = 10.44% * 3200;
Minibatch[ 513- 640]: loss = 0.247776 * 3200, metric = 9.03% * 3200;
Minibatch[ 641- 768]: loss = 0.231604 * 3200, metric = 9.06% * 3200;
Minibatch[ 769- 896]: loss = 0.229529 * 3200, metric = 8.62% * 3200;
Minibatch[ 897-1024]: loss = 0.214106 * 3200, metric = 8.25% * 3200;
Finished Epoch[1]: loss = 0.305012 * 25600, metric = 12.45% * 25600 4.119s (6215.1 samples/s);
error rate on an unseen minibatch 0.040000
5. What's Next ?
- CNTK 2.2 Python API に興味が持てたのであれば、次は CNTK 2.2 Tutorials に取り組まれるのが確実でしょう。
- ロジスティック回帰、MNIST、CIFAR-10 といったお馴染みのテーマについて詳しく解説されています。
- シリアル番号 100 番台 (CNTK-101, 102, 103, 104, 105 & 106) が初級チュートリアルに該当しています。
- また、Layers Library Overview (層ライブラリ概要) も興味深いです。
以上