CNTK 2.2 Python API 入門 (2) - 2 クラス分類問題 / Jupyter Notebook の活用
0. はじめに
◆ CNTK ( Microsoft Cognitive Toolkit ) 2.2 の Python API 入門第2弾です。
今回は 2 クラス分類問題を CNTK Python API で実装したロジスティック回帰と順伝播ネットワーク・モデルで解いてみます。
Jupyter Notebook (特に Azure NC 仮想マシン上での Jupyter Notebook) の利用方法についても詳述しました。
先の記事 で CNTK 2.2 では Python API が公開されていて、他の深層学習フレームワークと同様に
Python プログラムを作成することで深層学習モデルが構築できることがお分かり頂けたかと思います。
次のステップですが、現時点では CNTK の Python プログラミングに関する情報が少ない点を考慮して
引き続き、CNTK 2.2 Tutorials への橋渡しとなるような CNTK 2.2 Python API の入門記事を作成していきます。
※ Python と機械学習の基本的な知識を持つ読者を想定しています。
※ 他の深層学習フレームワークの経験があれば問題なく読み通せます。

◆ 前回はウォームアップ的な内容でしたが、今回から本格的な入門記事となります。
一般的な 2 クラス分類問題を CNTK Python API で実装したロジスティック回帰と順伝播ネットワーク・モデルで解いてみます。
Dense (完全結合) 層、cross_entropy_with_softmax 損失関数、sigmoid/softmax 活性化関数、sgd/adam learner (オプティマイザ) のような標準的な深層学習フレームワークでお馴染みのビルディング・ブロックも登場します。
チュートリアルのプログラムを参考にしながら、分かりやすい構成にして平易な言葉で説明することを心がけました。
入門という位置づけですので基礎理論にも言及はしますがそれは要点のみにとどめて、
CNTK Python API の説明を重視してプログラマ視点から実践的な内容にします。
初出の API には極力、リファレンス・マニュアルの該当箇所へリンクを張って参照しやすいようにしました。
具体的な内容は以下になります :
- Jupyter Notebook の活用
- 問題設定
- 本記事で使用する CNTK Python API
- ロジスティック回帰による解法
- 順伝播ネットワーク・モデルによる解法
- What's Next ?
CNTK のチュートリアルは Jupyter Notebook をベースにしていますので、最初に使い方を説明しておきます。
2, 4, 5 章は以下のチュートリアル2編を参考にしています :
1. Jupyter Notebook の活用
本編に入る前に、本記事でも CNTK チュートリアルでも Jupyter Notebook を多用しますので、
Jupyter Notebook の利用方法について説明しておきます。
※ Jupyter Notebook のリファレンスは The Jupyter notebook を参照してください。
※ 既に Jupyter Notebook を利用されている方はこの章はスキップして問題ありません。
1-1 動作環境
動作環境の構築が必要な場合には、Cognitive Toolkit 2.2 を Azure Linux GPU 仮想マシンにインストール を参考にしてください。Azure ポータルと Ubuntu Linux にある程度慣れていれば、30 分程度で以下のような環境が構築できるかと思います :
- Azure NC 仮想マシン with NVIDIA Tesla® K80 GPU
- Ubuntu 16.04 LTS
- NVIDIA CUDA 8.0 & cuDNN 6.0
- Anaconda 3 4.1.1
- CNTK 2.2 (for GPU)
1-2 Jupyter Notebook
1-2-1 jupyter コマンドの確認
上述の動作環境を利用する場合には、Jupyter Notebook は ~/anaconda3 ディレクトリ下に既にインストールされています :
$ which jupyter
/home/masao/anaconda3/bin/jupyter
$ jupyter notebook --version
4.2.1
あるいはより新しい Anaconda (例えば Anaconda3 4.3.1) であれば、
$ jupyter notebook --version
5.0.0
1-2-2 パスワード設定
安全に利用するために Securing a notebook server を参考にしてパスワードを設定しましょう。
(1) 最初に jupyter notebook --generate-config で config ファイルを生成します
(初めは config ファイルやそれを保持するディレクトリ ~/.jupyter は存在していません) :
$ jupyter notebook --generate-config
Writing default config to: /home/masao/.jupyter/jupyter_notebook_config.py
(2) 次に設定したいパスワードを元にしてハッシュ化した文字列を生成します。コマンドプロンプトで
python -c 'from notebook.auth import passwd; print(passwd())' と入力後、パスワードを (確認も含めて) 2回入力すると、sha1 ハッシュ値に変換してくれます :
$ python -c 'from notebook.auth import passwd; print(passwd())'
Enter password:
Verify password:
sha1:f0bb32803056:3e0773b7f13a88f36b8e9b9ba9fc05a3a73a1b05
(3) ハッシュ化されたパスワードを config ファイル (jupyter_notebook_config.py) 内の c.NotebookApp.password の値として手動で追記します。prefix の sha1: も含めてください :
$ vi ~/.jupyter/jupyter_notebook_config.py
# The string should be of the form type:salt:hashed-password.
# c.NotebookApp.password = ''
c.NotebookApp.password = 'sha1:f0bb32803056:3e0773b7f13a88f36b8e9b9ba9fc05a3a73a1b05'
これでパスワード認証ベースの Jupyter Notebook の起動が可能になります。
【補足】
Anaconda3 4.3.1 等に同梱されている Jupyter Notebook 5.0 の場合は上述の (1) ~ (3) の手続きは簡略化できます。
jupyter notebook password コマンドで、入力したパスワードをハッシュ化して新しい設定ファイル jupyter_notebook_config.json に自動追記してくれます :
$ jupyter notebook password
Enter password:
Verify password:
[NotebookPasswordApp] Wrote hashed password to /home/masao/.jupyter/jupyter_notebook_config.json
1-2-3 Azure ポータルによるポート開放
次に、Azure ポータルを利用して Jupyter Notebook が使用するポート (デフォルト : 8888/tcp) を開放します。
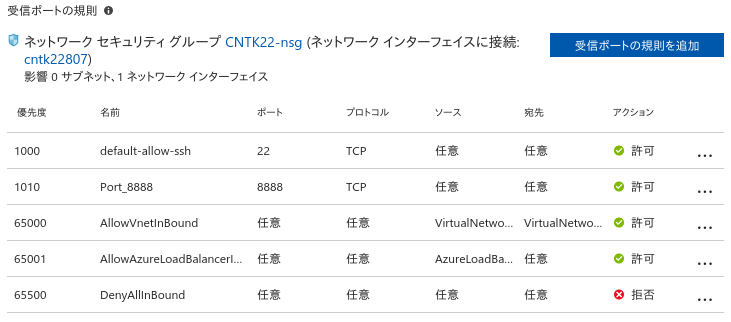
(1) Azure ポータルで仮想マシン詳細から「ネットワーク」メニューを選択すると次のような「受信ポートの規則」等を含む画面になります :

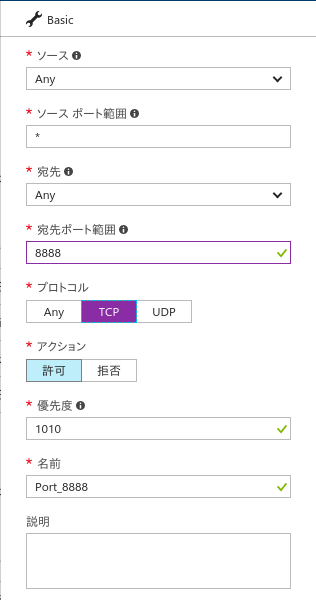
(2) ここで、「受信ポートの規則を追加」をクリックし、更に「詳細設定」をクリックすると、次のようなダイアログ・ボックスが表示されます :
ここで、宛先ポート範囲を "8888" として、プロトコルを "TCP" に設定します。その他のフィールドはデフォルトを使用して「OK」します。
(3) 新しいルールが追加されました。
1-2-4 Jupyter Notebook の起動
さて Jupyter Notebook サービスを起動しますが、jupyter コマンドを叩くディレクトリがそのままアプリケーションのルート・フォルダになりますので、先に適切なワークスペース・ディレクトリを作成しておいてください。
そのディレクトリで jupyter notebook --ip=0.0.0.0 --no-browser と入力すれば Jupyter Notebook の起動がかかります :
$ jupyter notebook --ip=0.0.0.0 --no-browser
[W 20:43:22.274 NotebookApp] Unrecognized JSON config file version, assuming version 1
[I 20:43:23.438 NotebookApp] [nb_conda_kernels] enabled, 1 kernels found
[I 20:43:23.499 NotebookApp] Writing notebook server cookie secret to /run/user/1000/jupyter/notebook_cookie_secret
[I 20:43:26.860 NotebookApp] [nb_anacondacloud] enabled
[I 20:43:26.863 NotebookApp] [nb_conda] enabled
[I 20:43:27.043 NotebookApp] ✓ nbpresent HTML export ENABLED
[W 20:43:27.043 NotebookApp] ✗ nbpresent PDF export DISABLED: No module named 'nbbrowserpdf'
[I 20:43:27.045 NotebookApp] Serving notebooks from local directory: /home/masao/ws.cntk/notebook
[I 20:43:27.046 NotebookApp] 0 active kernels
[I 20:43:27.046 NotebookApp] The Jupyter Notebook is running at: http://0.0.0.0:8888/
[I 20:43:27.046 NotebookApp] Use Control-C to stop this server and shut down all kernels (twice to skip confirmation).
1-2-5 Jupyter Notebook の利用
(1) アクセスとログイン
URL: http://(仮想マシン IP アドレス):8888 で Web ブラウザからアクセス可能です。
以下のような簡素なログインページが表示されますので、設定したパスワードを入力してください :

ログインに成功すると、以下のような画面になります。このケースではサーバ側の作業ディレクトリに何もない状態です :
(2) 新規ノート
2 章から実際に python コードを入力していくためには、新規ノートを作成する必要があります。
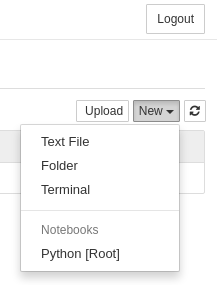
"Home" の画面の右上に "New" プルダウン・メニューがありますので、ここから "Python [Root]" (バージョンによっては "Python 3" と表示されます) を選択してください :
すると、以下のような新規ノートが新しいタブとともに作成されます :

この新規ページはデフォルトでは "Untitled" というような名前になっていますので、
"File" > "Rename..." メニューから適切な名前に変更しておきましょう。これはそのまま実際のファイル名にもなります。
(3) 入力
上図の新規ノートの画面中央にある、In []: に続く入力部をセルと呼称し、ここに Python コードを入力していきます。Shift + Enter で実行されます。その他、取り敢えず覚えておきたい操作として :
- "Cell" > "Cell Type" > "Markdown" メニューで、セルを Markdown モードに変更できます。Markdown モードでは Markdown が入力可能になります。
- ツールバーの "フロッピー・ディスク" ボタンをクリックすればノートを保存できます。
(4) 終了
Jupyter Notebook をサーバ側で終了するためには、^C を入力すれば良いです :
Shutdown this notebook server (y/[n])? y
[C 20:52:34.639 NotebookApp] Shutdown confirmed
[I 20:52:34.639 NotebookApp] Shutting down kernels
[I 20:52:35.140 NotebookApp] Kernel shutdown: defda64f-523a-4d4c-bdef-790e741b769b
2. 問題設定
本記事で通して扱う問題について説明します。この問題を CNTK で実装したロジスティック回帰と順伝播ネットワークで解くことになります。いささか大仰な切り口になっていますが、無味乾燥な合成データでもこのような意味を持たせるとイメージしやすくなるというメリットはあります。
【問題】 ある病院が患者から提供されたデータを持っていて、患者が悪性腫瘍を持つのか良性なのかを決定することを望んでいるとします。これは分類問題として知られています。各患者を分類することを助けるために、彼らの年齢と腫瘍のサイズが与えられています。直感的には、より若い患者 and/or 小さい腫瘍を持つ患者は悪性の腫瘍を持つ可能性が低いと仮定しても良いです。
本記事で扱うデータセットはこの問題を想起させる合成データになります。
◆ ここから Jupyter Notebook への入力が始まります。新しいノートが準備できていれば使い方は簡単です :
(1) 本記事中の In_[整数]==> で示される Python コード・ブロックを、ご自身で Notebook のセル (入力部) に入力しても良いですし、セルにコピー&ペーストしてもかまいません。
(2) 入力が完了したら必ず、セルを実行します。セルを実行するには、Shift + Enter を入力するか、
または下図のようなツールバーの青い丸印で囲まれた箇所をクリックします :

◆ 最初に CNTK で用意されているサンプル画像を表示してみましょう :
from IPython.display import Image
※ from IPython.display import Image を Jupyter Notebook のセルに入力したら、セルを実行します。セル実行後には新しいセルが出現します。
Image(url="https://www.cntk.ai/jup/cancer_data_plot.jpg", width=400, height=400)
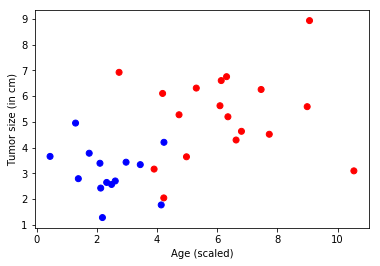
※ ここでも、Image(url="https://www.cntk.ai/jup/cancer_data_plot.jpg", width=400, height=400) をセルに入力したら、セルを実行します。すると、次のような画像が表示されるはずです。以後は逐一 Notebook の扱いに言及は致しませんが、実際に動作確認をされる場合には同様の操作を繰り返してください。
下のプロット図では、各観測データポイントはドットで表わされる患者です。そして赤色のドットは悪性であることを示し青色は良性であることを示しています :

【目標】 目標は、上述の問題に対する分類器を作成することです。
この分類器は2つの特徴 (患者の年齢と腫瘍サイズ) が与えられたときに、任意の患者を自動的に良性か悪性かのカテゴリーにラベル付けするものです。本記事では、ロジスティック回帰と順伝播ニューラルネットワーク・モデルのアプローチにより、CNTK で分類器を実装します。
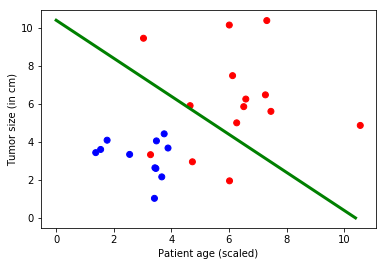
下図では、緑色の線がデータから学習されたモデルを表現していて赤いドットから青いドットを分離しています。(2, 3 のドットについては誤ったラベルを張っていますが。) 分類器の作成とは、緑色の線を学習するためのステップを進んでいくこととも言えます。
Image(url= "https://www.cntk.ai/jup/cancer_classify_plot.jpg", width=400, height=400)

3. 本記事で使用する CNTK Python API
今回使用する CNTK Python API を先にリストアップしてまとめておきます。
深層学習モデルの実装に必要なプリミティブが揃っていることが見て取れると思います。
◆ cntk.layers パッケージ
CNTK 層ライブラリです。今回は Dense 層のみを使用します。
cntk.layers.layers モジュール
Dense - 完全結合線形層のインスタンスを作成するための層ファクトリ関数です。
◆ cntk.learners パッケージ
トレーニング中にモデル・パラメータ・セットの調整をします。オプティマイザと考えて良いです。
learning_rate_schedule - 学習率スケジュールを作成します。
adam - モデル・パラメータを学習するために Adam learner インスタンスを作成します。
sgd - モデル・パラメータを学習するために SGD learner インスタンスを作成します。
◆ cntk.losses パッケージ
損失関数を含むパッケージです。
cross_entropy_with_softmax(output_vector, target_vector) - target_vector と output_vector の softmax 間の交差エントロピーを計算します。
◆ cntk.metrics パッケージ
評価メトリクスを含むパッケージです。
classification_error(output_vector, target_vector) - 分類エラーを計算します。
◆ cntk.ops パッケージ
CNTK のコア演算子を含むパッケージです。これらの演算子の呼び出しは CNTK 計算グラフのノードを作成します。
input_variable - ネットワークの入力を作成します : 特徴やラベルのようなデータが供給される場所で、いわゆるプレースホルダーです。
parameter - パラメータ・テンソルを作成します。
sigmoid - sigmoid 活性化関数です。
softmax - softmax 活性化関数です。
times - 乗算ですが、この演算の出力は2つの入力行列の積 (= matrix product) です。ブロードキャストをサポートします。
◆ cntk.tests.test_utils パッケージ
ユニット・テストのためのユティリティ。
set_device_from_pytest_env() - Jupyter Notebook 利用時に正しいターゲット・デバイスを選択するためのヘルパー関数です。
※ 総ての Jupyter Notebook の開始時にこれを呼び出す必要があります。
◆ cntk.train パッケージ
トレーニングのためのユティリティ・パッケージです。
cntk.train.trainer モジュール
Trainer - モデル・パラメータをトレーニングするクラス。
[メソッド]
test_minibatch - 指定されたバッチ・サンプル上でモデルをテストします。
train_minibatch - モデル・パラメータを最適化します。
[データ・デスクリプタ]
previous_minibatch_evaluation_average - 最後に訓練に使用されたミニバッチについてサンプルあたりの平均評価尺度値です。
previous_minibatch_loss_average - 最後に訓練に使用されたミニバッチについてサンプルあたりの平均訓練損失です。
4. ロジスティック回帰による解法
2 章で設定した問題を CNTK でロジスティック回帰モデルを実装することにより解いていきます。
機械学習の基礎理論に深入りはしませんが、要点だけ説明していきます。
CNTK Python API については使用するたびに説明していきます。
4-1 ロジスティック回帰とは
ロジスティック回帰は、入力特徴ベクトルの (線形の) 重み付けされた組み合わせを使用して異なるクラスを予測する確率を生成します。分類器が [0, 1] 内の確率を生成するとしたら、この値を (例えば 0.5 のような) しきい値と比較して二値ラベル (0 または 1) を生成することができます。
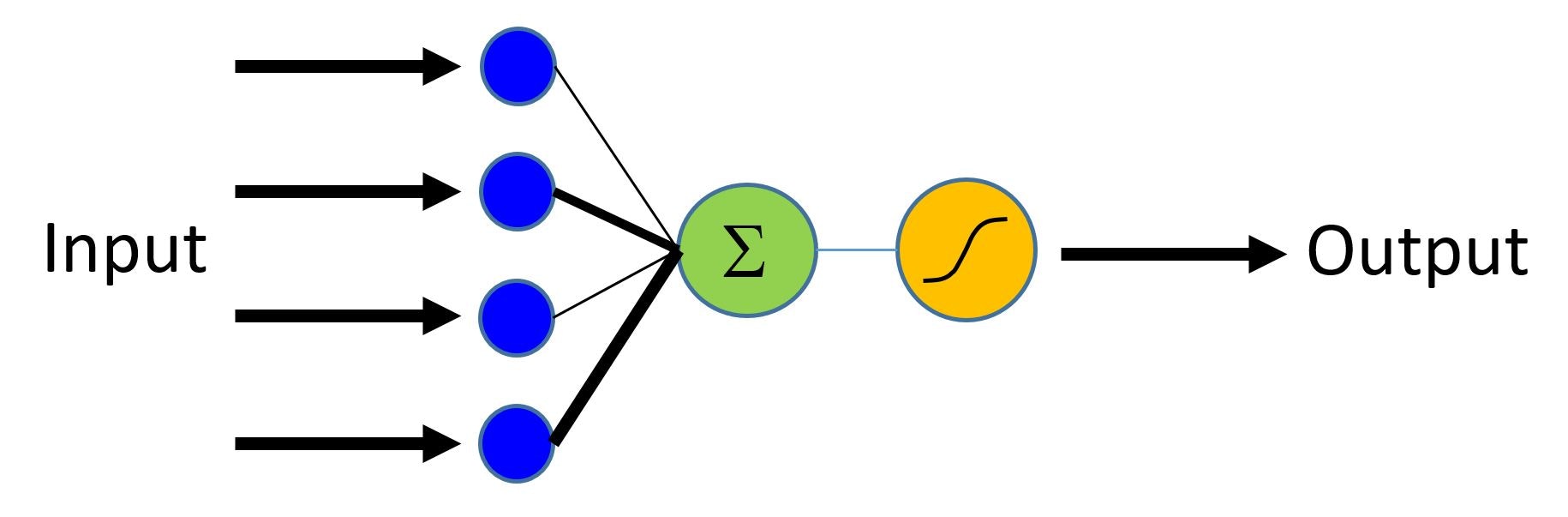
下図で言えば、異なる特徴入力からの寄与が線形に重み付けられて集計されます。
そして結果の総和は sigmoid 関数を通して (0, 1) 範囲にマップされます。また softmax 関数を使用して複数クラスについて拡張することもできます。
Image(url= "https://www.cntk.ai/jup/logistic_neuron.jpg", width=300, height=200)
4-2 インポート
ロジスティック回帰モデルを CNTK で実装するために、最初に必要なコンポーネントをインポートします :
from __future__ import print_function
import numpy as np
import sys
import os
import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env() # このシステムにだけ必要です。
C.cntk_py.set_fixed_random_seed(1) # このサンプルが再現可能であるようにシード値を固定。
cntk を C としてインポートしていますが、cntk.__init__ が主要なサブパッケージの名前空間を取り込んでいますので、これだけでサブパッケージの演算も利用可能になります。もちろんサブパッケージの演算を明示的にインポートしてもかまいません。
※ cntk.tests.test_utils サブパッケージの set_device_from_pytest_env は Jupyter Notebook でターゲット・デバイスを正しく選択するためのユティリティ関数です。
4-3 データ生成
課題である、癌患者サンプルをエミュレートする合成データを numpy で生成します。
このデータは、2 次元の入力特徴 (患者の年齢と腫瘍サイズ) と2つの出力クラス (良性/青色 or 悪性/赤色) を持ちますので、
input_dim と num_output_classes の設定は次のようになります :
input_dim = 2
num_output_classes = 2
さて実際に numpy を使用して合成データを生成しますが、実はこのデータは CNTK 2.2 Python API 入門 - データ生成 で使用したものと全く同じものです。データの生成手順についての説明は、そちらを参照してください。
np.random.seed(0)
def generate_random_data_sample(sample_size, feature_dim, num_classes):
# NumPy を使用して合成データを作成する。
Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes)
# データが分離可能であることを確かなものとする
X = (np.random.randn(sample_size, feature_dim)+3) * (Y+1)
X = X.astype(np.float32)
# クラス 0 をベクトル "1 0 0 " に変換し、
# クラス 1 はベクトル "0 1 0" へ, ...
class_ind = [Y==class_number for class_number in range(num_classes)]
Y = np.asarray(np.hstack(class_ind), dtype=np.float32)
return X, Y
ここでは、患者の年齢と腫瘍サイズの特徴を持つ訓練データの各データポイントが青色か赤色のラベルを持っているようなデータセットと考えて差し支えありません。但し、出力が one-hot ベクトルに変換されている点には注意しましょう。
※ one-hot ベクトルは一つの要素だけが 1 で他の要素は総て 0 なベクトルで、扱いやすいために機械学習で良く利用されます。
この入力データを matplotlib で可視化して冒頭のようなデータとなっていることを確認しておきましょう :
mysamplesize = 32
features, labels = generate_random_data_sample(mysamplesize, input_dim, num_output_classes)
# データをプロットします。
import matplotlib.pyplot as plt
%matplotlib inline
# 0 は悪性/赤色、1 は良性/青色を表わします。
colors = ['r' if label == 0 else 'b' for label in labels[:,0]]
plt.scatter(features[:,0], features[:,1], c=colors)
plt.xlabel("Age (scaled)")
plt.ylabel("Tumor size (in cm)")
plt.show()
4-4 モデル概要
ロジスティック回帰は単純な線形モデルで、入力として特徴ベクトル $\bf{x}$ を取って エビデンス (証拠・根拠) ($z$) を出力します。
下図で、入力層の特徴ベクトルは青いノードで表わされ、特徴の各々は相当する重み $w$ により出力ノードに接続されています (重みは太さが変化している黒いラインで示されています)。
エビデンスは緑色のノードの出力に該当します。
Image(url= "https://www.cntk.ai/jup/logistic_neuron2.jpg", width=300, height=200)
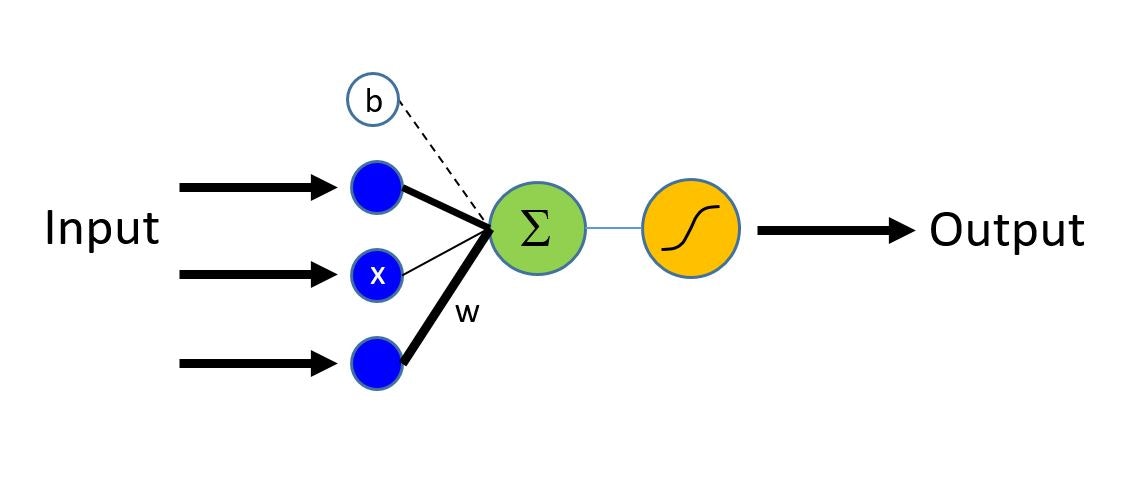
最初のステップは観測点に対するエビデンスを計算することです。$\bf{w}$ は重みベクトルで $b$ はバイアス項です (bold 表記はベクトルを示します) :
$$z = \sum_{i=1}^n w_i \times x_i + b = \textbf{w} \cdot \textbf{x} + b$$
エビデンスは (結果が 2 クラスの一つであるとき) sigmoid 活性化関数か
(結果が 2 よりも多い複数クラスの一つであるとき) softmax 関数を使用して (0, 1) 範囲にマップします。
4-5 ネットワーク構築
4-5-1 ネットワーク入力
ロジスティック回帰モデルのネットワーク定義は簡単ですが、最初に CNTK のプレースホルダーについて説明しておきます。
feature = C.input_variable(input_dim, np.float32)
入力変数 input_variable() は CNTK の主要なコンセプトの一つです。ユーザ・コード向けのコンテナあるいはプレースホルダーで、モデルの訓練/評価中、ユーザ・コードはこのコンテナをモデル関数オブジェクトへの入力となるデータポイント (今回の例では (年齢, 腫瘍サイズ) を持つデータポイント) で満たしていきます。
入力の shape は提供されるデータの shape にマッチしていなければなりません。今回の例では次元は年齢と腫瘍サイズから input_dim = 2 となります。
4-5-2 ネットワーク定義
ネットワークを定義する関数 linear_layer は前節のエビデンスを計算する式 : $z = \textbf{w} \cdot \textbf{x} + b$ の率直な実装です :
# モデル・パラメータをストアする辞書を定義する
mydict = {}
def linear_layer(input_var, output_dim):
input_dim = input_var.shape[0]
weight_param = C.parameter(shape=(input_dim, output_dim))
bias_param = C.parameter(shape=(output_dim))
mydict['w'], mydict['b'] = weight_param, bias_param
return C.times(input_var, weight_param) + bias_param
cntk.ops.parameter はテンソル・パラメータを作成します。
次の2つの演算を行っています :
- CNTK の
times演算子を使用して重み ($\bf{w}$) に特徴 ($\bf{x}$) を乗算して、 - バイアス項 ($b$) を加算する。
そして z はネットワークの出力を表わすために使用されます :
output_dim = num_output_classes
z = linear_layer(feature, output_dim)
4-6 トレーニング
4-6-1 モデル・パラメータの学習
◆ ネットワークが定義されたので、モデル・パラメータ $\bf w$ と $b$ を学習させることを考えます。
そのための手続きとして、算出されたエビデンス ($z$) を softmax 関数を使用して予測された確率 ($\textbf p$) のセットに変換してやります :
$$ \textbf{p} = \mathrm{softmax}(z)$$
softmax は活性化関数で、累積されたエビデンスをクラスに渡る確率分布に正規化してくれます。
モデルのトレーニングとは、この生成された確率をデータポイントの正解ラベルにできる限り近づいたものにしていくことに他なりません。つまり、出力と正解ラベル間の差異を最小化する必要があります。
◆ このときに利用可能な損失関数としてはポピュラーな 交差エントロピー があります。
簡単に言えば、確率分布に直されたネットワーク出力と正解ラベルの差異をエントロピーという乱雑さを表わす尺度を利用して計算します。厳密に言えば、$p$ を softmax 関数から予測される確率、$y$ を訓練データポイントの正解ラベルとすると、以下のように定義されます :
$$ H(p) = - \sum_{j=1}^C y_j \log (p_j) $$
$C$ はクラスを意味し、クラス数は num_output_classes に等しいです。
◆ CNTK では cntk.losses.cross_entropy_with_softmax という便利な関数が用意されています。cross_entropy_with_softmax(z, label) は正解ラベル label と、ネットワーク出力 z の softmax 間の交差エントロピーを計算してくれます :
label = C.input_variable(num_output_classes, np.float32)
loss = C.cross_entropy_with_softmax(z, label)
4-6-2 評価
分類を評価するために、cntk.metrics.classification_error を利用して分類エラーを計算することもできます。これは (エラーを計算するのが目的ですから) モデルが正しい場合 - つまり真のラベルに多くの確率を割り当てた場合には 0、そうでない場合には 1 になります :
eval_error = C.classification_error(z, label)
4-6-3 trainer を構成する
◆ モデル・パラメータのトレーニングを駆動する cntk.train.Trainer クラスのインスタンスである trainer は最適化テクニックを使用して loss 関数を最小化していきます。今回の例では最も基本的な確率的勾配降下 (SGD, Stochastic Gradient Descent, cntk.learners.sgd ) を使用します。
トレーニング手順としては :
(1) 最初にモデル・パラメータ (今回のケースでは、重みとバイアス) のランダム初期化から開始します。明示的に初期化しないときは通常はデフォルトの手法で初期化されます。
(2) そして各観測、つまり各データポイントの供給に対して、sgd オプティマイザは予測されたラベルと相当する正解ラベル間の loss (損失) を計算して、各観測後にモデル・パラメータの新しいセットを生成するために勾配降下を適用します。
(3) このモデル・パラメータの更新を繰り返して最適化していきます。
ミニバッチ
各観測後にモデル・パラメータを更新するプロセスはデータセット全体がメモリにロードされることを必ずしも必要としません。
より少数のデータポイントに渡る勾配を計算することで巨大なデータセット上のトレーニングを可能にします。
けれども、一度のステップで単一の観測データポイントだけを使用して生成された更新は反復のたびに激しく変化してしまいます。そのため妥協点として、観測データポイントの小さいセットをロードして、モデル・パラメータを更新する際にそのセットからloss の平均を使用することを考えます。このサブセットはミニバッチと呼称されます。
学習率
最適化の主要なメタ・パラメータの一つは learning_rate (学習率) です。
各反復においてパラメータをどのくらい変化させるかを調節するスケーリング因子と考えれば良いです。
◆ これらの情報で trainer を作成する準備が整いましたので、Trainer クラスをインスタンス化しましょう。
Trainer コンストラクタの基本的な引数は、モデル、損失関数等の評価尺度のタプル、learner (オプティマイザ) のリストです :
# モデル訓練を駆動する trainer オブジェクトをインスタンス化します。
learning_rate = 0.5
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
learner = C.sgd(z.parameters, lr_schedule)
trainer = C.Trainer(z, (loss, eval_error), [learner])
次に幾つかヘルパー関数を作成しておきますが、これらは進捗を可視化するためだけに必要なものです :
# 移動平均 (= moving average) を計算するユティリティ関数です。
def moving_average(a, w=10):
if len(a) < w:
return a[:]
return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]
# 訓練の進捗を出力表示するユティリティを定義します。
def print_training_progress(trainer, mb, frequency, verbose=1):
training_loss, eval_error = "NA", "NA"
if mb % frequency == 0:
training_loss = trainer.previous_minibatch_loss_average
eval_error = trainer.previous_minibatch_evaluation_average
if verbose:
print ("Minibatch: {0}, Loss: {1:.4f}, Error: {2:.2f}".format(mb, training_loss, eval_error))
return mb, training_loss, eval_error
4-6-4 trainer を実行する
ロジスティック回帰モデルを実際にトレーニングする準備ができました。
各反復は minibatch_size 25 サンプルを使用するものとして、総計 20,000 データポイント上でトレーニングしましょう。
反復数は num_minibatches_to_train で表わされます :
# trainer のためのパラメータを初期化します。
minibatch_size = 25
num_samples_to_train = 20000
num_minibatches_to_train = int(num_samples_to_train / minibatch_size)
これらのメタ・パラメータの設定後、trainer.train_minibatch メソッドによるトレーニングを実行に移せます。トレーニングに殆ど時間はかかりません :
from collections import defaultdict
# trainer を実行してモデル訓練を遂行します。
training_progress_output_freq = 50
plotdata = defaultdict(list)
for i in range(0, num_minibatches_to_train):
features, labels = generate_random_data_sample(minibatch_size, input_dim, num_output_classes)
# 入力変数にミニバッチ・データを割り当てて、そのミニバッチ上でモデルを訓練します。
trainer.train_minibatch({feature : features, label : labels})
batchsize, loss, error = print_training_progress(trainer, i,
training_progress_output_freq, verbose=1)
if not (loss == "NA" or error =="NA"):
plotdata["batchsize"].append(batchsize)
plotdata["loss"].append(loss)
plotdata["error"].append(error)
Minibatch: 0, Loss: 0.6931, Error: 0.32
Minibatch: 50, Loss: 4.4290, Error: 0.36
Minibatch: 100, Loss: 0.4585, Error: 0.16
Minibatch: 150, Loss: 0.7228, Error: 0.32
Minibatch: 200, Loss: 0.1290, Error: 0.08
Minibatch: 250, Loss: 0.1321, Error: 0.08
Minibatch: 300, Loss: 0.1012, Error: 0.04
Minibatch: 350, Loss: 0.1076, Error: 0.04
Minibatch: 400, Loss: 0.3087, Error: 0.08
Minibatch: 450, Loss: 0.3219, Error: 0.12
Minibatch: 500, Loss: 0.4076, Error: 0.20
Minibatch: 550, Loss: 0.6784, Error: 0.24
Minibatch: 600, Loss: 0.2988, Error: 0.12
Minibatch: 650, Loss: 0.1676, Error: 0.12
Minibatch: 700, Loss: 0.2772, Error: 0.12
Minibatch: 750, Loss: 0.2309, Error: 0.04
ここで、(ssh 接続した) bash シェル上で nvidia-smi コマンドを実行してみると、以下のように GPU メモリが割り当てられたことが分かります :
$ nvidia-smi
Sun Oct 1 21:17:54 2017
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 384.66 Driver Version: 384.66 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 Tesla K80 Off | 0000D31D:00:00.0 Off | 0 |
| N/A 51C P0 56W / 149W | 94MiB / 11439MiB | 0% Default |
+-------------------------------+----------------------+----------------------+
+-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 5675 C /home/masao/anaconda3/bin/python 83MiB |
+-----------------------------------------------------------------------------+
$ ps aux | grep -y 5675
masao 5675 1.5 0.6 81401832 361532 ? Ssl 21:10 0:07 /home/masao/anaconda3/bin/python -m ipykernel -f /run/user/1000/jupyter/kernel-623ca85b-58c4-48c3-8854-896ebb5705c7.json
masao 6221 0.0 0.0 15236 988 pts/1 S+ 21:18 0:00 grep --color=auto -y 5675
※ Jupyter Notebook のセルからでも最初に ! を付けることでシェルコマンドを実行することができます。
さて、トレーニング中に保持しておいた plotdata を利用して訓練の進捗を可視化してみましょう :
# 移動平均を計算して SGD におけるノイズを排除してスムースにします。
plotdata["avgloss"] = moving_average(plotdata["loss"])
plotdata["avgerror"] = moving_average(plotdata["error"])
# 訓練損失と訓練エラーをプロットします。
import matplotlib.pyplot as plt
plt.figure(1)
plt.subplot(211)
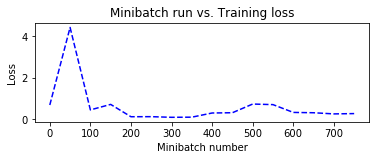
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel('Minibatch number')
plt.ylabel('Loss')
plt.title('Minibatch run vs. Training loss')
plt.show()
plt.subplot(212)
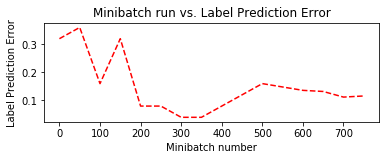
plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--')
plt.xlabel('Minibatch number')
plt.ylabel('Label Prediction Error')
plt.title('Minibatch run vs. Label Prediction Error')
plt.show()
4-7 評価
4-7-1 テストを実行する
訓練時に使用してないデータを使用して訓練されたネットワークを評価しましょう。
新しいデータを作成してこのデータセット上で trainer.test_minibatch メソッドを使用して平均エラーと損失を評価します :
test_minibatch_size = 25
features, labels = generate_random_data_sample(test_minibatch_size, input_dim, num_output_classes)
trainer.test_minibatch({feature : features, label : labels})
0.12
このエラーが訓練エラーよりも大きな差で大きい場合には、訓練されたモデルは (訓練中に見ていない) 新規のデータ上では上手く動作していないことを示しています。この状態を汎化性能が出ていないと表現しますが、要因としてはオーバーフィッティングなどがあげられます。
※ ここでは単一のミニバッチ上でテストしましたが、実際には、テストデータの幾つかのミニバッチを実行して平均を取る等の措置を取るべきです。
4-7-2 予測を確認する
より具体的に評価するために、ネットワーク出力を cntk.ops.softmax を通して (悪性/良性の) 2つのクラスに渡る確率分布に変換しましょう :
out = C.softmax(z)
result = out.eval({feature : features})
ネットワーク定義には softmax を含めていなかったことを思い出してください。
そして予測を正解ラベルと比較してみましょう。これらは一致しているべきです :
print("Label :", [np.argmax(label) for label in labels])
print("Predicted:", [np.argmax(x) for x in result])
Label : [1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1]
Predicted: [1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1]
np.argmax は最大値のインデックスを返します。予測に適用される場合には 2 クラスのうちの予測確率の大きい方のインデックスを返すことになります。大部分は一致しているものの、残念ながら、4, 5, 6 番目の要素に誤ったラベルを張っているようです。
4-7-3 可視化
結果を可視化できるならば、それは望ましいことです。誤分類となった要因も確認できるでしょう。
幸い今回の例では、入力データのために x-軸を患者年齢・y-軸を腫瘍サイズとして2つの空間次元を使用し、
そして出力のためには悪性を赤色・良性を青色としてカラー次元を使用して都合よくプロットできます :
print(mydict['b'].value)
bias_vector = mydict['b'].value
weight_matrix = mydict['w'].value
import matplotlib.pyplot as plt
colors = ['r' if label == 0 else 'b' for label in labels[:,0]]
plt.scatter(features[:,0], features[:,1], c=colors)
plt.plot([0, bias_vector[0]/weight_matrix[0][1]],
[ bias_vector[1]/weight_matrix[0][0], 0], c = 'g', lw = 3)
plt.xlabel("Patient age (scaled)")
plt.ylabel("Tumor size (in cm)")
plt.show()
[ 7.99141502 -7.99141407]
5. 順伝播ネットワーク・モデルによる解法
2 章で設定した問題の解法として、ロジスティック回帰の次に、順伝播ネットワーク・モデルでも試してみましょう。
モデル作成・ネットワーク定義部以外は、ロジスティック回帰と概ね同じコードを使用しますので、
そこでは要点以外は同じ説明を繰り返さずにコード・ブロックのみを掲載していきます。
◆ ここで、今までに入力したコードの副作用がないように、Jupyter Notebook で新しいノートを作成して使用しましょう。
手順としては :
(1) 最初に、今まで使用していたノートを閉じて、"Home" でそのノートを選択した上で shutdown をクリックして (Python コードを実行する) カーネルを停止します。この操作で GPU メモリが開放されます :
(2) そして新しい Jupyter Notebook ページを開くためには "Home" のページの右上に "New" プルダウン・メニューがありますので、ここから "Python [Root]" を選択してください :
5-1 順伝播ネットワーク・モデルとは
前章ではロジスティック回帰を使用して線形分類器をトレーニングしましたが、特徴をどのように構築するかの知識が殆ど得られないようなデータにおいては線形分類器はデータを正確にモデル化できずに、精度の限界を見る結果になりがちです。そのため (分類するための) より複雑な決定境界を持つモデルが必要となります。
順伝播ニューラルネットワークは最も単純なタイプの人工のニューラルネットワークです。
そのモデルは決定境界がロジスティック回帰のような単純な線形モデルよりも複雑なケースでも対応できるように、
複数の (ロジスティック回帰からの) 線形分類器を非線形分類器として結合します。
下図は典型的な順伝播ネットワークの形状を示します。
このネットワークでは情報は一つの方向へだけ移動します - 前方へ、順方向へ、入力ノードから隠れノードを経由して出力ノードへです。ユニット間の接続は循環を形成しません。ネットワークに循環やループはありません。
from IPython.display import Image
Image(url="https://upload.wikimedia.org/wikipedia/en/5/54/Feed_forward_neural_net.gif", width=200, height=200)

5-2 インポート
必要なコンポーネントをインポートします。ロジスティック回帰の場合と全く同じです :
from __future__ import print_function
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sys
import os
import cntk as C
import cntk.tests.test_utils
cntk.tests.test_utils.set_device_from_pytest_env()
C.cntk_py.set_fixed_random_seed(1)
5-3 データ生成
使用するデータセットもロジスティック回帰で使用したものと全く同じものです。課題の癌患者サンプルをエミュレートする合成データです。
2 次元の入力特徴 (患者の年齢と腫瘍サイズ) と2つの出力クラス (良性/青色 or 悪性/赤色) を持ちますので、
input_dim と num_output_classes の設定は次のようになります :
np.random.seed(0)
input_dim = 2
num_output_classes = 2
患者の年齢と腫瘍サイズの特徴を持つ訓練データの各データポイントが青色か赤色のラベルを持っているようなデータセットを生成すると考えて良いです :
def generate_random_data_sample(sample_size, feature_dim, num_classes):
Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes)
X = (np.random.randn(sample_size, feature_dim)+3) * (Y+1)
X = X.astype(np.float32)
class_ind = [Y==class_number for class_number in range(num_classes)]
Y = np.asarray(np.hstack(class_ind), dtype=np.float32)
return X, Y
※ 出力が one-hot ベクトルに変換されている点には注意しましょう。
※ データの生成手順についての説明は CNTK 2.2 Python API 入門 - データ生成 を参照してください。
5-4 モデル概要
作成する順伝播ネットワークは下図のような単純なものです。隠れ層2つ、それぞれの層は 50 のノードを持つものとします :
Image(url="http://cntk.ai/jup/feedforward_network.jpg", width=200, height=200)

各隠れ層のノード (上図では緑色) の数 hidden_layers_dim を 50 に、そして隠れ層の数 num_hidden_layers を 2 に設定します :
num_hidden_layers = 2
hidden_layers_dim = 50
5-5 ネットワーク構築
5-5-1 ネットワーク入力
最初に入力変数を定義しておきます :
input = C.input_variable(input_dim)
label = C.input_variable(num_output_classes)
入力変数 input_variable は CNTK の基本コンセプトの一つで、コンテナあるいはプレースホルダーでした。
モデルの訓練/評価中、このコンテナをモデルへの入力となるデータポイント (今回の例では (年齢, 腫瘍サイズ) を持つデータポイント) で満たしていきます。
5-5-2 ネットワーク定義 - 参考実装 -
今回のモデルのネットワーク定義は CNTK の層ライブラリ・パッケージ cntk.layers を利用すれば簡単です。
これは他のフレームワークでも標準装備されている層ライブラリと同様のものです。
けれども、理解の助けとするために、本節では CNTK のプリミティブな演算だけを使用して順伝播ネットワークをワンステップずつ定義します。
※ 本節 (5-5-2) のコードブロックは Jupyter Notebook に入力する必要はありませんので、ご注意ください。
◆ まず、一つの線形層を構成する linear_layer 関数を作成します。
最初の隠れ層を考えると、入力として次元 input_dim ($m$ とします) の特徴ベクトル ($\bf{x}$) を取り、次元 hidden_layer_dim ($n$ とします) のエビデンス $\bf{z_1}$ を出力します。
入力の各特徴は隠れ層の出力と、次元 ($m \times n$) を持つ行列 $\bf{W}$ で表わされる重みで結びついていることになります。
必要なステップは、特徴セット全体のためのエビデンスを計算することです :
$$\bf{z_1} = \bf{W} \cdot \bf{x} + \bf{b}$$
- $\bf{b}$ は次元 $n$ のバイアス・ベクトルです。
- bold 表記は行列/ベクトルを示します。
linear_layer 関数では、2つの演算を実行します :
- 重み ($\bf{W}$) に特徴 ($\bf{x}$) を乗算し、
- バイアス項 $\bf{b}$ を加算する。
cntk.ops.parameter はテンソル・パラメータを作成し、cntk.ops.times は入力行列の積 (matrix product) を計算する CNTK の演算です :
def linear_layer(input_var, output_dim):
input_dim = input_var.shape[0]
weight = C.parameter(shape=(input_dim, output_dim))
bias = C.parameter(shape=(output_dim))
return bias + C.times(input_var, weight)
※ このブロックをはじめ、本節 (5-5-2) のコードブロックはあくまで参考です。Jupyter Notebook への入力は不要です。
◆ 次のステップは非線形関数 - 活性化関数を通して、線形層の出力であるエビデンスを変換します。
活性化関数はエビデンスを活性化関数の値域の範囲に押し込めてくれます。
sigmoid や tanh が歴史的に有名ですが、最近では ReLU やその亜種が使用されることが多いです。
ここでは sigmoid 関数を使用します。sigmoid 関数の出力はしばしば次の層への入力か最終層への出力となります。
次の dense_layer 関数は隠れ層の実装となり、線形層に与えられた活性化関数 nonlinearity を適用します :
def dense_layer(input_var, output_dim, nonlinearity):
l = linear_layer(input_var, output_dim)
return nonlinearity(l)
◆ 一つの隠れ層のための関数を dense_layer として作成しましたが、多層ネットワークを構成するためには層を反復する必要があります。
今回の例では 2 層だけを持つので、単純に dense_layer を2つ並べても良いです。
この場合、次のようにコードを書けるでしょう。最初の層 $\bf{h_1}$ の出力は次の層の入力になります :
h1 = dense_layer(input_var, hidden_layer_dim, sigmoid)
h2 = dense_layer(h1, hidden_layer_dim, sigmoid)
けれども、より多い層にも対応しやすいように次のように書く方がベターでしょう :
def fully_connected_classifier_net(input_var, num_output_classes, hidden_layer_dim,
num_hidden_layers, nonlinearity):
h = dense_layer(input_var, hidden_layer_dim, nonlinearity)
for i in range(1, num_hidden_layers):
h = dense_layer(h, hidden_layer_dim, nonlinearity)
return linear_layer(h, num_output_classes)
ネットワーク出力 z はネットワークに渡る出力を表わすために使用されます。
これで完全結合ネットワークによる分類器ができました :
z = fully_connected_classifier_net(input, num_output_classes, hidden_layers_dim,
num_hidden_layers, C.sigmoid)
5-5-3 ネットワーク定義 - CNTK 層ライブラリの利用 -
cntk.layers API リファレンス / 層ライブラリ・リファレンス
前節で定義したネットワークは、CNTK プリミティブを使用してどのようにネットワークを実装するのかを理解する助けとはなりますが、実際には CNTK の層ライブラリを使用する方が遥かに簡単で高速です。
CNTK は事前定義されたポピュラーな「層」をビルディング・ブロックとして提供しています。
これは他のフレームワークでもお馴染みのもので、ネットワーク・デザインを単純化します。
具体的には、例えば、先に定義した dense_layer 関数の機能のためには Dense 層関数が用意されています。
層については、API レファレンス以外にも 層リファレンス が用意されています。
以下の実装は、前節の数ブロックに渡る参考コードを CNTK 層ライブラリでカプセル化して再定義したものです。
※ このブロックから Jupyter Notebook への入力を再開してください :
def create_model(features):
with C.layers.default_options(init=C.layers.glorot_uniform(), activation=C.sigmoid):
h = features
for _ in range(num_hidden_layers):
h = C.layers.Dense(hidden_layers_dim)(h)
last_layer = C.layers.Dense(num_output_classes, activation = None)
return last_layer(h)
z = create_model(input)
5-6 トレーニング
トレーニングの実装もロジスティック回帰と概ね同じですので、要点だけ説明しておきます。
5-6-1 tainer を構成する
◆ 損失関数にはロジスティック回帰と同じ cntk.losses.cross_entropy_with_softmax を使用します。
cross_entropy_with_softmax(z, label) は正解ラベル label と、ネットワーク出力 z の softmax 間の交差エントロピーを計算してくれます :
loss = C.cross_entropy_with_softmax(z, label)
◆ 分類を評価するために、cntk.metrics.classification_error を利用して分類エラーを計算することもできます。
これは (エラーを計算するのが目的ですから) モデルが正しい場合 - つまり真のラベルに多くの確率を割り当てた場合には 0、そうでない場合には 1 になります :
eval_error = C.classification_error(z, label)
◆ モデル・パラメータのトレーニングを駆動する cntk.train.Trainer クラスのインスタンスである trainer は最適化テクニックを使用して loss 関数を最小化していきます。
オプティマイザには基本的な確率的勾配降下 (SGD, Stochastic Gradient Descent, cntk.learners.sgd ) を使用します。
これらの情報で Trainer クラスをインスタンス化します。
Trainer コンストラクタの基本的な引数は、モデル、損失関数等の評価尺度のタプル、learner (オプティマイザ) のリストです :
learning_rate = 0.5
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
learner = C.sgd(z.parameters, lr_schedule)
trainer = C.Trainer(z, (loss, eval_error), [learner])
ちなみに、SGD の代わりに例えば Adam ( cntk.learners.adam ) を使用する場合は、次のようにすれば良いです :
learning_rate = 0.5
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
learner = C.adam(z.parameters, lr_schedule, 0.9)
# learner = C.sgd(z.parameters, lr_schedule)
trainer = C.Trainer(z, (loss, eval_error), [learner])
◆ 次に幾つかヘルパー関数を作成します。これらは進捗を可視化するためだけに必要なものです :
def moving_average(a, w=10):
if len(a) < w:
return a[:] # Need to send a copy of the array
return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]
def print_training_progress(trainer, mb, frequency, verbose=1):
training_loss = "NA"
eval_error = "NA"
if mb%frequency == 0:
training_loss = trainer.previous_minibatch_loss_average
eval_error = trainer.previous_minibatch_evaluation_average
if verbose:
print ("Minibatch: {}, Train Loss: {}, Train Error: {}".format(mb, training_loss, eval_error))
return mb, training_loss, eval_error
5-6-2 trainer を実行する
モデルをトレーニングする準備ができました。
各反復は minibatch_size 25 サンプルを使用し、総計 20,000 データポイント上でトレーニングします。
反復数は num_minibatches_to_train で表わされます :
minibatch_size = 25
num_samples = 20000
num_minibatches_to_train = num_samples / minibatch_size
これらのメタ・パラメータの設定後、trainer.train_minibatch メソッドによるトレーニングを実行に移せます。トレーニングに殆ど時間はかかりません :
training_progress_output_freq = 20
plotdata = {"batchsize":[], "loss":[], "error":[]}
for i in range(0, int(num_minibatches_to_train)):
features, labels = generate_random_data_sample(minibatch_size, input_dim, num_output_classes)
trainer.train_minibatch({input : features, label : labels})
batchsize, loss, error = print_training_progress(trainer, i,
training_progress_output_freq, verbose=0)
if not (loss == "NA" or error =="NA"):
plotdata["batchsize"].append(batchsize)
plotdata["loss"].append(loss)
plotdata["error"].append(error)
このタイミングで、GPU メモリが消費されます。
また、トレーニングの進捗として Loss/Error を出力表示させたい場合は、print_training_progress の引数で verbose=1 としてください。
plotdata を利用して訓練の進捗を可視化します :
plotdata["avgloss"] = moving_average(plotdata["loss"])
plotdata["avgerror"] = moving_average(plotdata["error"])
import matplotlib.pyplot as plt
plt.figure(1)
plt.subplot(211)
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel('Minibatch number')
plt.ylabel('Loss')
plt.title('Minibatch run vs. Training loss')
plt.show()
plt.subplot(212)
plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--')
plt.xlabel('Minibatch number')
plt.ylabel('Label Prediction Error')
plt.title('Minibatch run vs. Label Prediction Error')
plt.show()
SGD に加えて、Adam によるトレーニング時のグラフも合わせて掲載しておきます。
Adam の方が収束が速いですが、すぐにオーバーフィッティングの傾向が見られます :
| 損失 | エラー | |
|---|---|---|
| SGD | 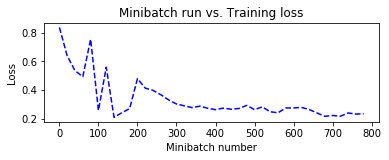 |
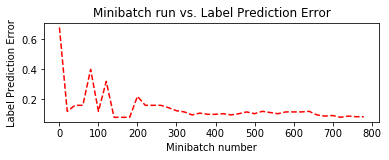 |
| Adam | 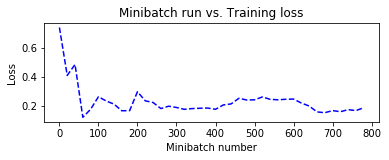 |
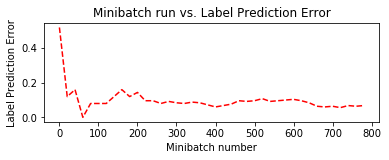 |
5-7 評価
訓練時に使用してないデータを使用して訓練されたネットワークを評価します。
新しいデータを作成してこのデータセット上で平均エラーと損失を評価するために、trainer.test_minibatch が利用できます。
test_minibatch_size = 25
features, labels = generate_random_data_sample(test_minibatch_size, input_dim, num_output_classes)
trainer.test_minibatch({input : features, label : labels})
0.12
より具体的に評価するために、ネットワーク出力を softmax を通して (悪性/良性の) 2つのクラスに渡る確率分布に変換します :
out = C.softmax(z)
predicted_label_probs = out.eval({input : features})
そして予測を正解ラベルと比較してみましょう。
これらは一致しているべきですが、ロジスティック回帰でも問題になっていた 3 点についてはやはり分類を誤っています :
print("Label :", [np.argmax(label) for label in labels])
print("Predicted:", [np.argmax(row) for row in predicted_label_probs])
Label : [1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1]
Predicted: [1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1]
6. What's Next ?
CNTK 2.2 Python API をマスターするためには Tutorials が最適ですが、本記事は以下のチュートリアル 2 編をカバーしています :
従って、他の初級チュートリアルに該当する CNTK-103, 104, 105 & 106 に取り組むのが良いでしょう。
以上