おはようございます。
スイスはジュネーブの多国籍企業でハードウェア製品のプロダクトマネージャーをやっている傍ら、趣味で人工生命や創発・進化の研究をしている @lucas29liao です。
本職は2児のパパです。
生命の進化と技術の進化に類似点があると感じることが多くなり、最近話題になることの多いブロックチェーン、量子コンピュータ、人工知能の共進化にまつわる素材を備忘録にまとめてみました。
上記技術の関係者にとっては新鮮味のない自明の投稿かと思いますし、肝心の箇所の考察ができていなかったりするのですが、おさらいという意味合いで書いていきます。
ブロックチェーンについてのおさらい
Blockchainの定義は関係者間でも合意されたものはありませんが、ひとまず古典的な(?)ブロックチェーンについておさらいをしましょう。
まず取引について
古典的なBlockchainが管理の対象とするのは、公開鍵暗号を用いた署名を利用し、従来立会人が担っていた、①本人承認、②債務履行拒否の防止、③取引内容の改ざん防止、という役割を肩代わりさせた取引です。
Private Keyを用いてTransaction内容にかけた署名はPublic Keyを用いた演算でしか検証できないという関係と、Public KeyからPrivate Keyの特定が現実的に不可能であるという性質から①本人認証が行えます。
また、Private Keyを持つのは自分なので②債務履行拒否が防止できます。
他の人はPrivate Keyを知らないので、Transactionを改ざんしようにもPublic Keyを用いて署名を確認できるような形にできず、③取引の改ざんも防止できます。
このような取引内容が公開されていれば、世の中の誰もが全ての取引を計算することができ、仲介者や監査する役目 (銀行など) がなくても自律的に管理できるようになるというアイデアが出発点です。
三者以上に取引が広がる時は、ある取引のユニーク性を証明するハッシュを(BitcoinではSHA256を二重に)計算し、次の取引データに記載します。これで、新しい取引は以前の取引を参照することになります。
ただ、これが行われた時点で他のメンバはその取引の存在を認識していないので2重取引が可能です。
そこで、全員が取引に立会い、同時に記帳することを考えます。しかし、誰かがオフラインになっていたらこの仕組みは成り立ちません。
ここで Proof of Work (PoW) を導入します。承認をするのにコストがかかるようになると、承認者が多くなると(私怨などの場合を除き)悪者のモチベーションは無くなります。
PoWの導入は、偽アカウントの大量発行の対策にもなります。
BitcoinのPoWはSHA-256 x 2で生成するハッシュ値の先頭にx桁の0がなくてはいけないという制約によって実現されます。
ブロックについて
ここまではBlockは出てきませんでした。なぜBlockが必要なのでしょうか?
取引をして承認を求めるユーザーにとっては、手数料は安くないと困ります。承認する側は、PoWの労力以上のメリットが必要です。
そこで、複数の取引をまとめて承認する(手数料総額が多くなる)ことができるようにします。
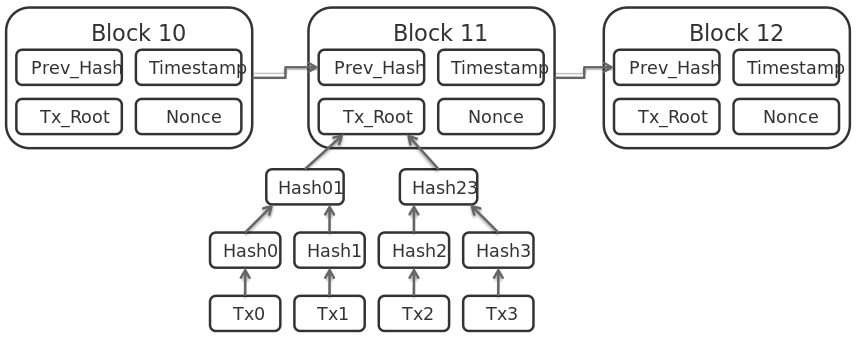
こうして取引をまとめたものがBlockで、それぞれのBlockは直前のBlockを参照して繋がっているのでBlockchainと呼ばれます。
承認者は手数料の総額が採算の合う数だけ積み上がれば、新しいBlockの中に2重取引がないことなどを確認した上で手数料を表した取引を追加し、PoWて取得した条件を満たすハッシュやそのインプットに利用したnonce、時刻などを記載した上で、Blockを締めて市場に宣言します。
取引当事者は、Blockの中身を確認することで、取引を正式に完了することができます。
もちろん作業内容が重複することがあるので、承認者は作業をやり直すことになるケースは発生します。
一時的に記載データに不整合が出ることを許容するが、最終的には参加者全ての記載データが同じものに収束していくシステムです。
重要な前提
おさらいしてみると、Blcokchainが利用した技術的アイデアとして
- 公開鍵暗号 (署名
- ハッシュ関数 (承認
があります。
立会人なしの取引のために、Private Keyを用いた署名もPublic Keyを用いた演算での署名検証も簡単だが、Public KeyからPrivate Keyを特定するのは現実的に不可能という性質を持つ関数が要請されます。
また、分散ネットワークを採用するために、2重取引の防止や偽アカウントの大量発行などの対策が必要です。そのために (PoW以外にも承認方法は色々提唱されていますが、Bitcoinでは) PoWのような承認コストの導入が必要です。
これは別にハッシュ関数である必要はないのですが、前のブロック情報を引数に取りつつ、繰り返し何度も出題できる手間のかかる問題である必要はあります。そして検算が簡単である必要もあるし、また実用上、問題の難度を操作できることが望ましいです。
ここで、入力値が違えば出力が予想できない形で大きく変わり、入力データ長に関わらず出力値が固定の長さで、かつ $hash(x) = h$ の計算は簡単だが $hash^{-1}(h) = x$ の計算は困難という性質を持つハッシュ関数を使った問題が条件に合うし扱いやすいので採用されました。
これらの前提が、別の技術の進化によって崩れるとシステム全体に問題が起きます。
そういうことは起き得るのでしょうか?
実は量子的な演算が、Blockchainが要請すのアイデアを守るためにも使えそうだし、破るためにも使えそうです。
ここで量子コンピュータについておさらいする必要があります。
(Blockchain自体の改良についてはまた触れます)
量子コンピュータについてのおさらい
はじめに
学部生の頃に量子コンピュータ関係の講義を履修した記録は残っているのですが、セメスターが終わって3歩あるいたらすっかり忘れてしまったようなので、割とミーハー状態で書きます。
ベースとなる認識
量子コンピュータにも明確な定義はありません。と言いますか、違う種類のものがごっちゃに説明されていると言うべきかもしれません。
私が大学で量子コンピュータ関係の講義を受けた時は専らゲート方式/回路型のものを指していた記憶がありますが、2011年にカナダのD-Waveが商用化し有名になった量子アニーリング方式などもあります。
が、ひとまずBlockchainと関連して議論をするために、量子アルゴリズムを実行することで古典コンピュータを超える計算能力を持つ計算機、という意味で量子コンピュータを捉え、主にゲート方式についておさらいをします。
本記事の後半、AIとの関連を話す時にもうちょっと広義に量子コンピュータを議論します。するかもしれません。。
量子演算と、素因数分解について
量子コンピュータはbitではなくqubitを使います。
bitが0か1のどちらかの状態を取るのに対し、qubitは0と1を同時に取るようなsuperposition/重ね合わせ状態という状態を取ることができ、n個のqubitが2^n個の状態を同時に表すことができます。
これは0と1の中間でもなければ、確率的に0か1の状態にある訳でもありません。一般的に複素数の確率振幅と呼ばれる値で量子状態が表現されます。確率振幅は位相という情報も含んでいます。この概念を導入することで説明できる量子現象が数多くあります。
確率振幅は正の値も負の値も(複素数も)取ることができるため、量子状態を重ね合わせた時に強めあったり、打ち消しあったりする効果が得られます。
 [Quantum Optics and Quantum Many-body Systems](http://qoqms.phys.strath.ac.uk/research_qc.html)
[Quantum Optics and Quantum Many-body Systems](http://qoqms.phys.strath.ac.uk/research_qc.html)
また、entanglementという現象を利用したアルゴリズムを利用することで、古典コンピュータとは別オーダーの計算量で、そのアルゴリズムが対象とする問題を解くことが可能です。
entanglementはqubitの集合の取る状態が、1つ1つのqubitの状態の集合として表せない状態のことで、2つのqubitの状態を切り離して考えることができない状態です。回転ゲートだけでは作れませんが、制御NOTゲートを使って計算する時に必然的に現れます。
ここで注意が必要なのは、量子コンピュータがいつくかの問題を高速で解けるのは古典コンピュータのアナロジーでクロックが速いといったような理由ではなく、ある種の計算に対して膨大な数の並列計算ができるからです。また、どんな問題でも早く解けるという訳ではありません。
しかし、「高速に解ける」とされる問題の中には、Blockchainが利用する公開鍵暗号が安全性の根拠とする問題も含まれます。
ちょっと見てみましょう。
Shorのアルゴリズムについて
量子アルゴリズムの一例として、因数分解を高速に解くShorのアルゴリズムというものがあります。
アルゴリズム全体の概要は Wikipedia に読みやすくまとまっています。
量子アルゴリズム部分はまた別の資料 ( 量子を学ぼう など?)を参照して頂きたいのですが、
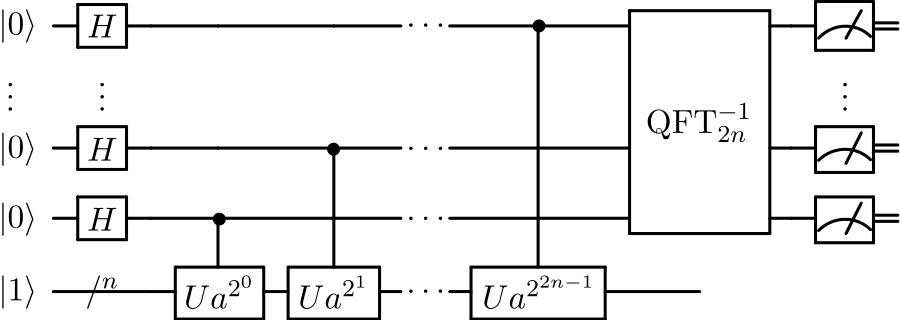
- 入力レジスタ(レジスタ1)に量子フーリエ変換を作用させ(Hadamard変換と同処理: 下図H)重ね合わせ状態をつくり、
- レジスタ2(下図左下 $ \lvert 1 \rangle $ で初期化されているレジスタ)でレジスタ1の入力を引数に持つmod関数を計算
- ここでレジスタ1(の一部)とレジスタ2との間にentanglement関係ができる。
- その後レジスタ2を観測することで、レジスタ1をある周期的な確率振幅を持つ状態にした後
- レジスタ1に逆量子フーリエ変換を作用させ(これをしないと、レジスタ1はそれが取れる全ての場合を平均的に観測されてしまう)
- 最後にレジスタ1を観測するというものです。
このShorのアルゴリズムを含む、従来のアルゴリズムを凌ぐ代表的な量子アルゴリズムのほとんどは以下のような手順を踏むようです。
- 入力にHadamard変換をかけ(るなどし)て重ね合わせ状態を作る
- これにより、使用できるqubit数が多くなるにつれて指数的に並列状態を計算できます
- Hadamard変換は 量子コンピュータをリモートで制御・観測しながら量子ゲートの基本を理解 でも少し扱いましたが、x軸とz軸の中間軸を中心に180度回転させる操作に相当します。
- その入力に対して特定の演算をし、「入力」と「演算結果」の間にentanglement関係をつくる
- Shorのアルゴリズムにおいて、この演算はモジュロ演算になります。また、Shorのアルゴリズムではレジスタ2の観測も行います。このステップはなぜ必要なのでしょうか?レジスタ2の観測値に対応するように、レジスタ1はある周期に合わせた状態の時だけ0でない確率振幅を持つことになるからです。ここで量子フーリエ変換の出番です。
- 最終的に計算したい演算結果のみを残す
- 確率振幅の干渉を利用して、適さない演算結果が観測される確率を打ち消しあう方向の干渉で低くして、適した演算結果が観測される確率は増幅方向の干渉で高めることで、限られた状態に収束する
- Shorのアルゴリズムの場合、最後の量子フーリエ変換を行う前は、入力レジスタは等しい確率振幅でレジスタ2の観測値に対応する全ての可能なビット状態が観測されるはずですが、その「可能な状態」はとある周期を取ります。ここで量子フーリエ変換を用いることで、その周期がある整数を使って量子化される条件のものを観測する確率を増幅することができます。こうして周期性を抽出します。
- ここが一番難解、かつShorのアルゴリズムを含む多くの量子アルゴリズムにおけるキーだと思います。
上記ステップ1で記述したように、量子アルゴリズムには使用できるqubit数が多くなるにつれて指数的に並列状態を計算できるという性質があります。
しかし、一般的にこれだけではあまり意味がありません。並列状態をそのまま観測しても普通は全ての状態を平均的に観測してしまうからです。
そこで、最終的に欲しい状態に収束し観測を行う必要があります。このためにShorのアルゴリズムでは量子フーリエ変換を用いましたが、重ね合わせとentanglementによりこの処理の計算力が古典的コンピュータと量子コンピュータでは全く違ってきます。
量子コンピュータではN個の qubit に対して必要なゲートの数は$N(N+1)/2$にしかなりませんが、古典コンピュータでN bitのFFTを行うには$2^N$回程度の操作が必要です。N=100の場合、FFTでは$2^{100}$回の操作が必要になりますが、QFTでは約5000回のゲート操作で済みます。
これは操作数だけを見れば大変な簡素化です。しかし、アルゴリズム実行に必要なqubitは 2n 近くまで減っている ( Beauregardの回路 など) らしいものの、量子コンピュータで因数分解が高速に解ける?〜 ショアのアルゴリズム 〜 でも指摘されているように、2048bitの鍵長のRSA暗号に対応するには現在実現している数十qubitsの (ゲート方式) 量子コンピュータでは全く足りず、ノイズ解消なども考えると実用的な量子コンピュータの実現までの道は遥か遠いでしょう…
しかし、複数のqubitの状態を圧縮して別のqubitに保存するようなことができれば必要なqubit数は劇的に下がるかもしれませんし、ショアのアルゴリズムではなく量子アニーリング的な Adiabatic quantum computation により、少ないqubitで高速に素因数分解ができるという話もあります。2014年には4 qubitsで56153の素因数分解がなされたようですし、2016年には量子アニーリングコンピュータのD-Waveで200099の素因数分解がなされたようです。 この因数分解には2000 qubitsを持つD-Wave 2Xが使われていますが、論理処理を行うqubit毎に誤り訂正に~12qubitほど必要なので実際の処理に使えるのは~160 qubit程のようです。
もちろんこれらアニーリング方式の量子コンピュータのqubit数は、ゲート/回路型の量子コンピュータのqubit数と単純比較するようなものではありません。qubit同士のグラフ関係もありますし。
(アニーリング方式は最適化問題を解くことに特化していますが、素因数分解に用いる際の着想はとても単純で、$M=pq$ のとき $y=0$ となる $y=(M−pq)^2$ の最小値問題を解けば良いようですが、本稿では詳細には踏み込みません)
Blockchainと量子コンピュータにまつわる技術進化について
量子アルゴリズムと公開鍵暗号
ここで一旦公開鍵暗号に話を戻しますが、全ての公開鍵暗号が素因数分解の困難さを安全の根拠にしている訳ではありませんし、実はBitcoinも署名にRSA暗号は使っていません。
楕円曲線暗号
公開鍵暗号の中では楕円曲線暗号もポピュラーで、BitcoinではElGamal暗号を利用した楕円曲線DSAが使われています。(Bitcoinを技術的に理解するが大変わかりやすいです )
楕円曲線暗号については 技術勉強会(楕円曲線暗号)資料 や、もっと詳しくは 楕円曲線暗号入門 などを参照して頂きたいのですが、要は楕円曲線上の有理点の集合全体が加群構造を持つように演算$+$を定義し、(素数pを法として還元して考えた曲線の上で)この加算を繰り返すとう処理で暗号化します。
ちなみに楕円曲線$E$上の2つの有理点を結ぶ直線と$E$との交点も有理数だということに最初に気がついたのはニュートンらしいです。
通常のformulationでは、xy平面にはありませんがy軸上の無限遠にあると捉えた点 $O$ を与え、加算対象$P,Q$を結ぶ直線と楕円曲線が交わる点のx軸対称の点を$P+Q$としています。
 ([E is for Elliptic Curves](https://www.maths.ox.ac.uk/about-us/life-oxford-mathematics/oxford-mathematics-alphabet/e-elliptic-curves))
([E is for Elliptic Curves](https://www.maths.ox.ac.uk/about-us/life-oxford-mathematics/oxford-mathematics-alphabet/e-elliptic-curves))
この加群のうち、$P+Q = Q+P, P+O = P, P+(-P) = O$を示すのは簡単ですが、$P+(Q+R) = (P+Q)+R$を示すのは格段に難しいようです。ここで1)楕円関数論の加法定理を応用するか、2)3次曲線の交点に関する幾何学の定理を使うか、3)証明などに関わらずそういうものだと納得する、という3つの道がります。私は工学系研究科の卒業生であることに誇りを持っているので3の道を取りました。
また、楕円曲線上にいつくかの点$P_1, ..., P_s$が取れて、全ての有理点Pが
$P = n_1P_1 + ... + n_sP_s$ ($n_1, ..., n_s $ は整数 )
という形に表せる。つまりいくつかの点をあらかじめ選んでおけば、全ての点がこれらの和・差から得られる = 有限生成であるというモーデルの定理: 「楕円曲線上の有理点の全体は有限生成の加群を成す」が根底にあります。
楕円曲線は単なる曲線のことなのに、面白いことに群構造を持ち、しかもその中で有理点の全体は有限生成になっていると言うのは感動的です。
有限生成の加群というのは構造が簡単な部類で、数学科の学生は2~3年生レベルで「有限生成加群の構造定理」を習うそうです。
私は数学科の卒業生ではないので楕円曲線についてはこのくらいにして先に進みますが、楕円曲線も数多の数学の進化の上で育った領域です。
楕円曲線暗号に話を戻すと、ここで議論したかったポイントは、ElGamal暗号などの楕円曲線暗号が安全性の根拠とする離散対数問題もShorのアルゴリズムを改良することで高速に(多項式時間で)解けるようだということです。
細かな詳細がきちんと追えませんでしたが、とにかく2つのmodular exponentiationsと2つの量子フーリエ変換を使い、そして素因数分解のアルゴリズムとは違い、2つではなく3つのレジスタを使う方法が提唱されています。
離散対数問題は生成元$g$を固定して $g^x = y $ mod $p$ を考えると、$y$が与えられた時に$x$を求める問題ですが、ここで $f(a,b) = g^a y^{-b}$ mod $p$ というmodular exponentiationを導入し、この関数が周期的な関数になることを利用します。この周期は$f(a,b) = g^{a-xb}$ mod $p$ と書いた時の$x$に依存し、例によってフーリエ変換による周波数成分分解でxを取り出せるというおおまかな流れのようです。
詳細は現在5歳の息子が物理学科に進んだ時にちゃんと教えてもらうことにします。
量子アルゴリズムと暗号・署名
Shorのアルゴリズム的なアルゴリズムを現実的に実行できる量子コンピュータや、Adiabatic quantum computation等を利用するコンピュータによりRSA暗号や楕円曲線暗号が将来的に破られる可能性はあります。しかしBlockchainが要請する公開鍵暗号という技術的アイデアのキーは、上の方で触れたように、Private Keyを用いた署名もPublic Keyを用いた演算での署名検証も簡単だが、Public KeyからPrivate Keyを特定するのは現実的に不可能という性質を持つ関数です。
今の暗号が破られても、別のアルゴリズムを利用することで、公開鍵暗号は進化を遂げ生き延びるかもしれません。
例えば格子暗号というものがあります。
詳しくは格子暗号の実用化に向けて などを参照して頂きたいのですが、20年くらいという比較的浅い歴史を持つ公開鍵暗号です。
安全性根拠とする問題は、Shortest Vector ProblemやClosest Vector Problemというものです。
例えばShortest Vector Problemでは、
格子基底 $v_1, v_2, ... , v_m$ が与えられた時、格子 $L (v_1, v_2, ... , v_m)$ に属するゼロでない最短のベクトルを求めるという問題です。
 ([Security+ Guide to Network Security Fundamentals](https://www.emaze.com/@ALQOLQWZ))
([Security+ Guide to Network Security Fundamentals](https://www.emaze.com/@ALQOLQWZ))
この図では、長い2つのベクトルが与えられた時に左下の方の起点から垂直に伸びている最短ベクトルを求めるという問題です。2次元上での図示を見ると、なんだかチョロそうな問題に見えます…ほんとに難しいんでしょうか?
この問題の難しさは、最短ベクトルを与える基底ベクトルの係数が無数に取れることと、さらにこれがn次元ベクトルになるとnの指数的な組み合わせを考えないと最短ベクトルを見つけられないという所にあります。しかし、なぜこれが量子アルゴリズムで解けないのでしょうか?
ちゃんとした理解はできませんでしたが、NP困難な問題は量子コンピュータが利用できても効率的には解けないという予想があり、Shortest Vector ProblemやClosest Vector Problemは(特定の条件下で)NP困難だと示されているようです。
詳しくは現在3歳の娘が数学科に進んだ時にちゃんと教えてもらうことにします。
格子暗号が安全性根拠とする問題についてはわかったということにして、ではこれを公開鍵暗号にどう利用するのでしょうか?
例えばShortest Vector Problemの困難性を利用するAjtai-Dwork暗号は以下のような方式を取ります。
- 秘密鍵
- ベクトル $r_1,..., r_{n-1}$ と、それらの線形結合で表される超平面$H$に対してある程度距離が離れたランダムなベクトル $r_n$
- 公開鍵
- 格子$L(r_1,..., r_n)$ に対してランダムな基底
- 暗号化
- バイナリ列を暗号化します
- 0 > ランダムに格子点を選び、微小なランダムベクトルを加える
- 1 > 単にランダムなベクトルに変換する
- バイナリ列を暗号化します
- 復号化
- 超平面 $H$ と平行な超平面は周期的に現れるので、いずれかの超平面との距離を計算する。
- 距離が小さければ > 0に復号
- 距離が小さくなければ > 1に復号
- 超平面 $H$ と平行な超平面は周期的に現れるので、いずれかの超平面との距離を計算する。
超平面$H$に平行な格子中の平面は $r_n$ に対応するある程度の距離をもって等間隔に現れるという構造ですが、それが分かるのは秘密鍵を持っている人だけという仕組みです。
(量子コンピュータは公開鍵暗号にとって脅威なのか?)
では、これをBlockchainで利用するための署名に使えるでしょうか?
ここで署名アルゴリズムについて書こうかと思ったのですが、ややマイナーな話題ですのでまた別の機会にします。
この格子暗号は量子コンピュータを利用したアルゴリズムではありませんでしたが、量子コンピュータを積極的に使った暗号というアイデアもあり、古くから様々提唱されております。
中でも古く有名なのが、暗号化アルゴリズムそのものではありませんが量子鍵配送です。
解説はネット上に無数に見つかる記事に譲りますが、entanglement状態にある量子を使い、途中で盗聴(観測)されると、entanglement状態が解除されるのでそれが検知できる仕組みです。
これによって安全なPrivate Keyを取得することができるとされます。ワンタイムキーとして使えば原理上破られない暗号が実現します。
光子を偏光状態で送るだけなので現存する光ファイバ網で対応可能とも言われますが、送り手と受け手の両方に単一光子源や単一光子検出器の両方が必要など現実的ではないとされていました。しかし、現在はレーザーやAPDを用いても安全性が示せるようになったようです。
ただ、これをblockchainで使おうとすると少なくとも大幅なシステム変更が必要になりそうです。通信の度に共通鍵を作成し直す必要がありますし、共通鍵なのでそもそもblockchainには使えないという指摘もありました。ただこれはアプリケーションサイドで何とかなる気がします。量子鍵配送は通信の安全性確認のために使い、それから別の承認アルゴリズムに基づいて取引記録をblockchainに記録していくといったような使い方はできそうです。
GoogleがChromeに実装したという話もありましたね。(New Hope)
ワンタイムなので20年後に実用的な量子コンピュータができても今のメッセージが安全、という話にはなるのでしょう。
また、2017年9月には中国科学院のチームが量子鍵配送を利用したワンタイム暗号を使ってウィーンと30分のビデオ会議を行う実験に成功したようです。暗号キーは高度500kmの低軌道を回っている墨子という人工衛星に搭載された装置が生成し、そこから送られたとのことです。
ここからの暗号を中国の光ファイバー網で国内各地に送信するインフラが既に整っていて中国政府の要人や軍幹部など600人が量子暗号を用いた通信網に接続できるとのことで、すごいですね。次は高軌道衛星を打ち上げ、中国の宇宙ステーションに量子通信装置を搭載し、最終的には一群の静止衛星で地球全体をカバーするのが目標だとか。ここまで長期の科学プログラムに大規模に投資をするビジョンがある中国の政治家ってのはすごい。
実用化は中国が先を行くのかもしれません。
ハッシュ関数について
hash関数にもいろいろありますが、SHA256の処理のイメージを掴むには SHA256の解説と実装 の解説が大変分かりやすいです。SHA256に関する最新のFIPSは更新され、こちらです。
また、Wikipedia: SHA-3にあるようにSHA2とは全く異なるSHA3もNISTで標準化されています。
ハッシュ関数は誤りチェックやチートチェック等にもよく使われます。
データの塊から特定のアルゴリズムを利用し、ハッシュ値を生成し、データとハッシュ値をペアで送信します。その後、受信したデータから再度ハッシュ値を求めて、一致していたらデータの破損なく配れたとする仕組みです。
PoWではnonceと呼ばれるハッシュ関数への入力をいろいろ変えて、出力が一定の条件を満たすかどうかでブロックの承認(マイニング)を行います。
では、量子コンピュータでこの承認・マイニング作業を超高速化することはできるでしょうか?
これができると、PoWを承認に利用するBlockchainシステムは突破される可能性があります。(とは言っても、Blockchainシステムの組み方次第で技術的にはどうとでもなると思います。しかし署名や承認のやり方を変更するとなるとコミュニティーで合意が取れずにまたハードフォーク、という可能性は高い気がします。)
またここで、①量子コンピュータで楕円曲線暗号を突破し公開鍵を逆算するという話と、②量子コンピュータで特定の条件を満たすハッシュ値を出力する入力を見つけるという話は行っている計算が違い、全く違う話であることに注意しましょう。)
ゲート方式/回路型のコンピュータを使う場合
まず、ゲート方式/回路型のコンピュータを利用する場合を考えてみましょう。
この場合、重ね合わせ状態のnonceを超並列処理するためにレジスタに置くことはできます。(※SHA256等の場合、ハッシュ関数はぐるぐる入力を回しながら処理するため、取引データ部分もbitではなくqubitを使う必要があります)
問題は、一定以下のハッシュ値を出力する場合の確率振幅を増幅して観測することができるかどうかです。
さてハッシュ関数(とりあえずSHA256)の処理を見てみると、古典コンピュータありきのアルゴリズムという気がプンプンするので、これを量子アルゴリズムで高速化できればいいのですが全く思いつきません。。
ここで私がうーんと考えても日が暮れてしまうので他文献を参照しますが、Instruction to post-quantum cryptographyやCost analysis of hash collisions: Will quantum computer make SHARCS obsolete?などでも、共通鍵暗号やハッシュ関数の安全性は量子アルゴリズムを実行できるコンピュータに対しても安全性は崩れないと解説されています。
次に、アニーリング的な方式のコンピュータを利用する場合を考えてみましょう。
この場合、重ね合わせ状態の入力に対して、一定以下のハッシュ値を出力するという問題を最適化問題に書き換えることができるかどうかが焦点です。
アニーリング方式コンピュータ上のアルゴリズム実装については詳しくないため正直よくわかりませんが、SHA256はじめ多くのハッシュ関数の処理の持つあからさまに人工的な処理との相性はやはり良くないように思えます。シフト演算的な処理もアニーリング方式では難しそうです。
この点についてはあまり詳しく書けないのでまた勉強します。
さてここまで見てきたように、Blockchainというアイデアを崩すためにも守るためにも量子的な演算というものが利用できそうです。
ただ、崩すサイドと守るサイドを比べると、崩すサイドへの貢献の方が大きそうです。特に公開鍵暗号を用いた認証については量子コンピュータはシステムを崩す用途に利用できますが、守る用途への貢献は限定的。しかし共有鍵暗号システムを守るという目的には利用できそうだというまとめをひとまずしておきます。(格子暗号は量子暗号ではありません)
Blockchainの進化・多様化について
Blockchainについては、ヨーロッバではイギリスと私の住むスイスに(は少なくとも)大変活発なコミュニティーがあります。
初めてSatoshiの論文を読みBlockchainの技術を知った時にはその工学的工夫の美しさに感動し、これまで誕生・進化して生き残ってきた公開鍵暗号やハッシュ関数などの関連技術、そして通貨というシステムの正統進化だと思った思ったものですが、そのBlockchainも日々進化しています。
また、例えばBlockchainの不可逆性は用途(詐欺や不正請求への対処など)によっては望ましくないこともありますが、不可逆性はベースレイヤーの技術特性であり、その上のアプリケーションの作り方によって取り扱いを可逆的にすることは可能なのでアプリケーションとして進化も進みます。
Bitcoinは匿名性や中央機関を持たないといった特徴がありますが、この特徴はBlockchainの技術特性ではないため、これらが望ましくない場合(犯罪利用や違法品の流通など)は中央機関を持ったアプリケーションを作ることもできます。
PoWには電力消費が多いという問題もありますが、これに対しては電力消費が少ないアルゴリズムを利用するという進化があり、商用のBlockchainでは電力消費が少ないアルゴリズムが使われることが多いようです。
(第三者機関を抜きに複数の会社がひとつの台帳を信用できるという可能性から、コンソーシアムBlockchainにも注目が集まっています。Dropboxのようなサービスでいいのでは?暗号化されてるし、ファイルの履歴も残るし、アクセス管理やストレージ上限設定なども柔軟にできるし。という突っ込みもありますが、柔軟なアプリケーションを構築するためにはコンソーシアム型のBlockchainが必要になります)
承認に時間がかかるという当初のBlockchainの欠点は、例えばRippleがIOU取引という形を取り入れました。コンソーシアム型で用いられることの多いPBFTもこの欠点を受けて進化した面があります。
新しいBlockchainシステムの承認を最初から安定させるためには事前に相当数の参加者が集まっている必要があるという問題には、既存のBlockchainの上にサービスを構築するという解決策が提示されました。Ethereumはその一つです。
PoWではなくPOSを利用する承認方法(マイニングの能力ではなくコインを持っている割合を基礎にコンセンサスを決めることで、アカウントの大量発行も意味がなくなるし、コインを大量に持つ人が取引を改ざんをしようにもシステム自体の信頼性を既存し自分を攻撃することになってしまう)、やNEMが採用するProof of Importanceという承認方法もあります。そしてブロックを使わず、有向非巡回グラフ(Directed Acyclic Graph)とTangleというアイデアを採用したIOTAなど、どんどん進化しています。
Bitcoinに代表される、通貨という初期のアプリケーションへの要請を受けて進化している面もありますが、例えば量子アルゴリズムといったような天敵候補の存在により、生き延びるために技術的進化を余儀なくされているという面もあります。
暗号技術と暗号解読技術のように、というのは一面的過ぎますが、Blockchainと量子コンピュータもまた共に属する生態系の中で共進化する存在なのです。
また、ものすごく雰囲気だけでいい加減なことを言いますが、Blockchainアプリケーション、そしてとりわけアルコインの今の状況は爆発的に多様性が生まれている状況で、カンブリア紀の多様性爆発に似ている気がします。
今から5億年以上前、カンブリア紀には無数の新種が突然生まれ、多様性が爆発的に増加しました。このときに、これまでにわかっているほぼ全ての動物門が出現したとされます。
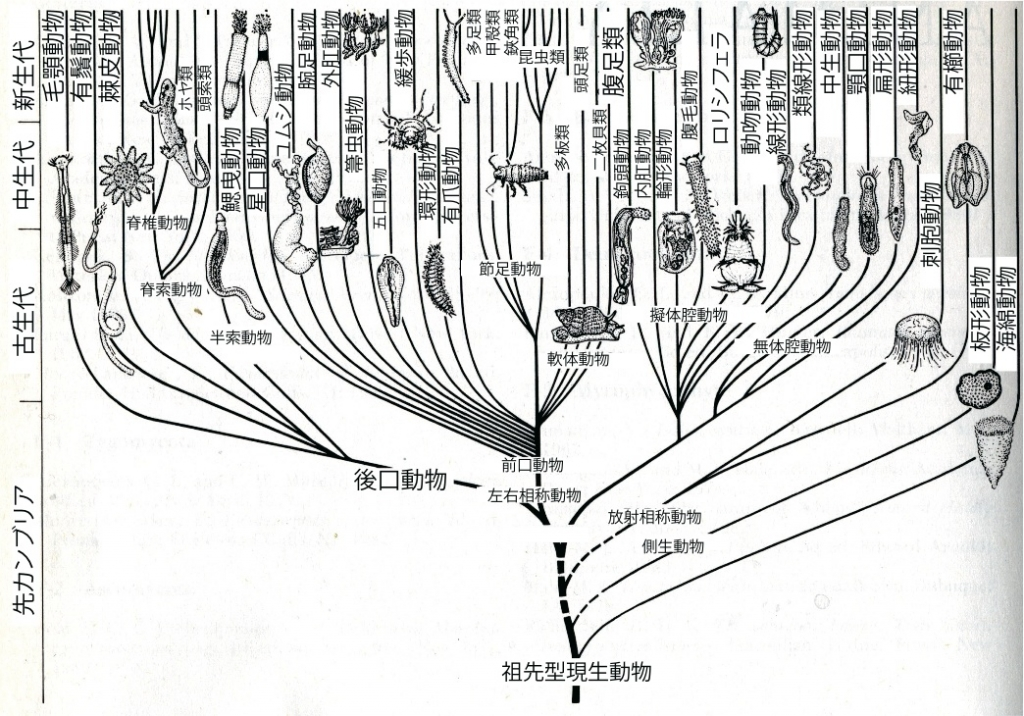
その後、ぺルム紀末の絶滅ではすべての種のうち95%が消えてしまったとも言われますが、その大絶滅後の進化とカンブリア爆発後の進化には非対称性が見て取れるとする説もあります。
スチュアート・カウフマンは以下のような考察をしています。
カンブリア紀の種の大爆発の不思議な特徴は、進化の図表が上から下に向かって埋められていったことにある。非常に異なった身体をもつ生物の「門」が多数生まれることにより、自然は急激に前進した。そして、この基本的なデザインがより精密化されることにより、網、目、科、属が形成されていったのである。2億5千万年前の二畳紀の絶滅では、すべての種のうち96%が消えてしまった。しかし、その反動期には様々な新しい科へ、目へ、網へ、そして門へと、多様化は下から上に進んでいったのだった。
もちろん「急激に前進した」の「急激」は地質学的に急激という意味で、数百万年を指しています。これは形態的な進化にとっては膨大な時間であり、化石の断絶は飛躍的進化の証拠にはなりません。
Blockchainアプリケーションの多様化・進化も急激と言えば急激ですが、ソフトウェア開発の営みとしては常識的な時間がかかっているとも言えます。
また、カウフマンは技術の進化とのアナロジーにも触れています。
私自身はカンブリア紀の爆発を、たとえばまったく新しく発明された自転車の技術的進化の初期段階のようなものだ、と考えている。前の車輪が大きく後ろの車輪が小さいもの、また後ろの車輪が大きく前の車輪が小さいものなど、初期の自転車の滑稽な形を思い出そう。ヨーロッパからアメリカ、そしてその他の場所にまで広がった多岐にわたる自転車の形の大混乱の中から、やがていくつかが主流として残り、他のものは非主流となった。大きな技術革新が起きたすぐあとでは、非常に異なる変形版を発見するのは容易である。しかし、のちの技術革新は、より最適化された設計に対するささやかな改良に限られてしまう。
カンブリア紀において、多細胞生物が、生き物としての可能な形をはじめて試してみたときにも、同様なことが起きたのではないかと私は考えている。もしビデオテープを再生するとしたら、分岐した個々の生命形態こそ異なるかもしれないが、はじめは劇的に、そしてのちにはしだいに細かく、詳細を変えていくという分岐のパターン自体は、同じように現れるのではないだろうか。生物の進化は、ダーウィンが教えたように非常に歴史的な過程であるのかもしれないが、同時に合法則的な過程でもあるのだ。
Blockchain、アルトコイン関係のアイデアやサービスも単なる分化と統合という訳でもなく、そのうち何かのきっかけでほとんどが急に滅びる大絶滅が起き、生き残ったものがインクリメンタルな小さな最適化を辿る、ということが起きるかもしれません。
そしてその時は、技術の進化にも生命の進化にも共通する、ユニバーサルな進化の理論のヒントが得られるかもしれません。漸進的な自然選択を補完し、そして技術の進化も説明する一般的進化理論が発見される日を待っていると想像するのは夢のあることです。
人工知能についてのおさらい
人工知能=AIは広く言えば自ら考えるマシンのことですが、方式としてはいろいろあります。
まず機械学習について、そしてその後議論に合わせて機械学習に限らない人工知能について触れたいと思います。
私は機械学習については2~3年前にCourseraのMachine Learningの講義を修了し、趣味や仕事でPythonでいろいろモデルを試してから、Andrew Ng先生の新しいDeepLearningコースを履修し、最近はIan Goodfellow氏のDeep Learningのテキストなど数冊の書籍を読みつつTensorflow等を使ってDeep Learningの基礎を勉強している程度の量産型データサイエンティストです。
最新の論文を積極的に読んでキャッチアップするような生活は送っておらず、いろいろ遅れた視点から書くことになるかもしれません。
機械学習について
産業応用的にはちょっと前、アカデミア的にはかなり前まではシンプルな教師あり学習(要は大規模な重回帰、input-outputの高精度マッピング、パターン認識)と教師なし学習(クラスタリングや異常検知、主成分分析やそれに近いものなど)、それからAmazonやNetflix始め様々なサービスで使われているリコメンダエンジンが大きな部分を締めていたと感じます。そしてそうそう、遺伝的アルゴリズムというのもあって組み合わせ最適化問題やプロダクトデザインに応用されたりしています。
そして本当にちょっと前には、大きなデータを学習でき、複雑・多層なDeep Learning、CNNの画像処理応用、そして提唱自体は古いもののRNNやLSTMなどの時系列データへの実用的な応用(音声認識、NLP)などDeep Learningが世間を驚かせました。
そして最近ではAlphaGo Zeroやロボットの自律行動学習など強化学習の応用例が目立ってきたり、教師あり学習を利用しているものの、アプリケーションしては従前と比べてかなり違うGANを利用した例が目立ってきていると感じます。漫画のカラー化とか、画風の模倣とか、馬をシマウマに変えたりとか、加齢に伴って将来顔がどう変わるかを予測したり。
もちろん教師あり学習も自動運転のような複雑なパイプラインのものの開発が進んだり、半教師あり学習、x-shot learningなど少ないデータからの学習を可能にする技術もホットです。
また、ホントお世話になったAndrew Ng先生は転移学習がフロンティアであるとも指摘しています。
いろいろ進化の方向はあれど、機械学習を含め人工知能、というかコンピュータ、ひいては人類が「機械」に対して求めるのは自動化だと思います。
基本的には人間は機械を使って、考えたりやったりするのが面倒なことを自動化したい。
シンプルな教師あり学習も、RegressionかClassificationかに限らず予測・判断の自動化。教師なし学習もデータの中に構造を発見する仕事の自動化。レコメンダエンジンも、嗜好に合った提案の自動化。Feature Learningは特徴量を見つけるのを自動化したという意味もありますね。そして強化学習は学習(ないし、例えば教師データを集めるような、学習のためのお世話の仕事)の自動化。GANは創作行為の自動化。自動運転や機械翻訳なんかはそのまま運転・翻訳の自動化です。
ここで真の自動化のためには、教師データ的なものやラベルを集めるような作業も自動でやってくれるようにならんかなぁ、そういうの欲しいなぁと思うわけです。教師データを集めるのは難しくて、実際世の中のほとんどのデータは教師なしデータなわけですし。
強化学習はその方向に乗った営みだと思いますが、難しさはいろいろあるようです。
例えば、Pieter Abbeel氏は強化学習について実用的にはこのような話をしています。
(※意訳です)
Deep Reinforcement Learningはいつもスクラッチで学習する。これをどうにかしたいが、まだ実現していない。例えばロボットに動作を学習させる時、学習初期には教師あり学習として人間の真似をするようにして、徐々に後半は強化学習に切り替え長期的に学習させるといったようなハイブリッドシステムが現実的だと思う。
Zeroの前のAlphaGoもそんな感じでしたね。
また、「真の自動化」という抽象的な方向の先には、教師なし学習があるのではないかという考えもあります。
例えばYoshua Bengio氏は以下のように言っています。
(※意訳です)
今の産業システムは教師あり学習を主に使ってるけど、教師なし学習は非常に重要。人間を見ると、非常に柔軟にいろんな仕事をしていることがわかる。世界を観察して、インタラクションを取って、探索しながら新しいコンセプトを見つけることができる。
2歳の赤ちゃんだって物理法則を理解してる。重力も、圧力も、慣性も理解してる。液体と固体の違いも理解してる。誰から教わったわけでもないのに。どうやって学習したのか?そういったものに答えを出そうというのが教師なし学習だ。
そこで最近は教師なし学習のアイデアと強化学習のアイデアを組み合わせる研究をしている。そこに重要な未知のコンセプトが隠れていると信じている。
ちなみに人間の学習は教師なし学習で学んだコンセプトに後からラベリングされるような半教師あり学習だという視点もごく自然で説得力がありますが、それも今のDeep Learningパラダイム的すぎる気もします。問題はその教師なし学習での学習って一体何なんだ?というところではないかと思います。
このように人間の赤ちゃんの実世界でのコンセプト学習を引用しつつ、たまに教師なし学習について耳にするのが、
- 教師なし学習は教師あり学習と比べて(ちゃんとした比較は難しいが)学習データが大量に必要そう
- そして例えば人間の赤ちゃんの学習過程は教師なし学習に近いところが多いのではないか
- 補足すると
- 人間の赤ちゃんにinputされるデータは例えば(生まれるまではひとまず置いといて)生まれてから3歳の誕生日までに1576800分の動画、音声、触覚、嗅覚、味覚というマルチモーダルデータと考えるとものすごい量という話
- 人間をアプリケーションと捉えた時の処理の柔軟さはすごい。これはデータ量と教師なし学習がキーではないの?という話
- 補足すると
- さらに飛躍すると、量子コンピュータは古典コンピュータと比べて計算が別オーダーで高速なので、量子コンピュータと大量のデータを使って汎用人工知能に近づけるのでは?という話。つまりAIの進化は量子コンピュータの計算力を要請する
といったような話です。
量子アルゴリズムと機械学習について
さて古典コンピュータがそうであったように、量子コンピュータもまた技術的生態系の中で他の技術や環境に影響を与えます。
機械学習も応用技術と考えると無関係ではいられないと考えるのは自然でしょう。
では、具体的にはどう影響されるのでしょうか?
ゲート方式
まずゲート方式/回路型の量子コンピュータとの関連を考えてみます。
論点をシンプルにしたいので、一般的な量子アルゴリズムとの関係について議論します。
上の方で触れましたが、量子アルゴリズムの多くは、①重ね合わせ状態をとった入力と、②その入力に対する演算との間にentanglement関係をつくり、③その関係を利用しつつ確率振幅をうまく処理して取り出したい状態の観測確率を上げる、といったものでした。
これは量子アルゴリズムの一般化ではないものの、今のところ一般的とは言っていいと思います。もちろん複数のentanglement関係を利用したり、複数の入力を使ったり、複雑な量子アルゴリズムも多いと思いますが、基本的な考え方としてはこういうものだ思います。
さて、最終的には大量の計算力を要求するとされる人間がやってみせるタイプの教師なし学習について考えてみたいですが、まずは教師ありの普通の(?)Deep Learningから考えてみましょう。
計算量がかかる理由はいくつかあります。
まず入力に扱うデータがリッチ。Mnistでさえ $28 * 28 = 784$ 次元のベクトル。これが高解像度(e.g., $4096*2160=8847360$)になると大変です。
凄い数ですねー。えっ違う?失礼しました。各ピクセルはRGBなのでその3倍ですね。
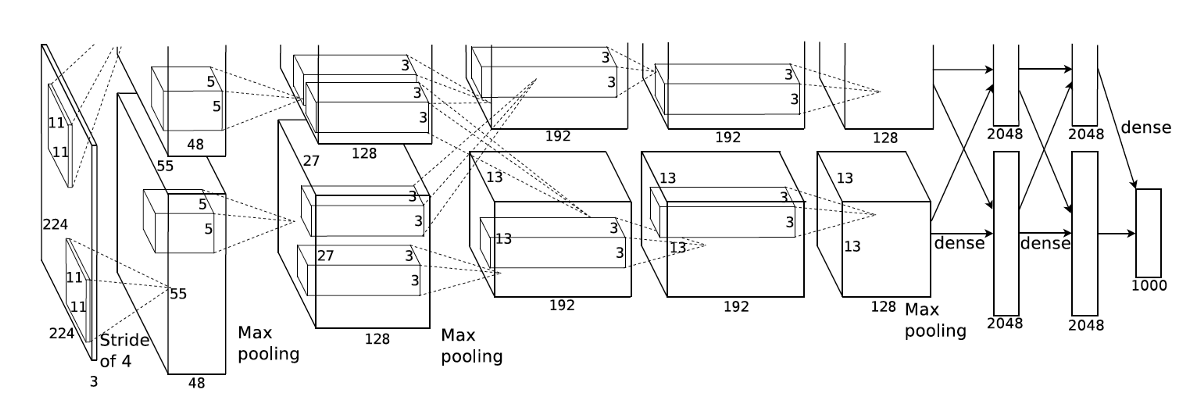
さらにけっこう複雑なモデルで学習させるとなると最適化するweightパラメータは数千万以上になることもあります。(AlexNetは6000万個と聞いてはえーと思いましたがこれなんかでは"1 billion trainable parameters"とも)
そしてこのweight最適化: 学習に使うデータですが、2016年時点で最低でも5000 labeled data per category、人間レベルのパフォーマンスを期待するなら1000万データくらいが目安とのことです。この数値はphoto object detectionイメージですかね。当然アプリケーションによって違うとは思いますけど、まあそのくらいとしましょう。
ここまでが主にデータとパラメータ量の膨大さによって計算量がかかる理由です。
入力データの重ね合わせ
このうち、「ラベル毎に5000データが必要、ないし人間レベルを求めるなら1000万データが必要」といった問題には量子重ね合わせ状態が利用できるかもしれません。が、実用上の壁はとてつもなく高いでしょう。
例えば $ \lvert 0010 \rangle, \lvert 0101 \rangle, \lvert 0110 \rangle, \lvert 1011 \rangle $ という4つの重ね合わせ状態を入力に使いたいとしましょう。画像とは呼べませんが、2x2ピクセルの白黒画像と捉えてください。この時、単純に4つのquibitにHadamard変換をかけるだけでは明らかに不十分で、$ \lvert 0010 \rangle, \lvert 0101 \rangle, \lvert 0110 \rangle, \lvert 1011 \rangle $ の4パターンのみを表すように各qubit間のもつれ状態を作る必要があります。実際に入力に使いたい数百万qubitの大規模なもつれ状態を保持したまま演算ができるとはとても考えられません。Shorのアルゴリズム等ではHadamard変換で一様な重ね合わせ状態の入力を作りましたが、ここでは入力パターンひとつひとつに制約がかかります。
weightパラメータの重ね合わせ
続いて、数千万というweightパラメータ数の対処ですが、これは学習アルゴリズムに多分に影響されます。入力と違い、異なる状態の重ね合わせを作る必要はないと考えられるので、量子アルゴリズムの恩恵を受けるのが難しい箇所かもしれません。
そして、もし処理の過程で重ね合わせ状態を作って高速化に利用できたとしても、Deep Neural Networkモデルは各ノードが多数のノードと繋がっており、全体としてひとつの巨大なクラスタを作っています。相転移モデルで言うとクラスタ数は1です。よってweightパラメータについても全てのノード同士の間にもつれ状態をつくる必要があります。
愚直に考えれば数億qubitのもつれ状態をつくる必要がありそうです。
入力データの次元の重ね合わせ
入力データの次元数(例えばMnistデータの $28 * 28 = 784$ 次元)を重ね合わせ状態を使って減らすのは不可能かと思われます。
学習と、学習結果の観測
また前述したように、重ね合わせで並列状態をつくるだけでは全ての状態を平均的に観測してしまうだけなのであまり意味がありません。欲しい状態に収束して観測を行う必要があります。
では、入力データやweightパラメータの重ね合わせ状態を保ったまま学習を行い、学習後のweightパラメータのみの確率振幅を増幅して観測するためにはどのようなハードルがあるでしょうか?
ここで、機械学習の学習アルゴリズムに踏み込む必要があります。
話を(私にとって)わかりやすくするために、最適化にはCNNを使う場合についてまず考えてみましょう。
CNNは…といっていくつかの限定的なケースについて検討しようとして気が付いたのですが、それぞれの学習アルゴリズムへの量子アルゴリズム利用について書いていると日が暮れてしまうし、それ以前に力不足だと気が付きました。
更なる考察はまたの機会にしようと思います。
アニーリング方式
また、量子コンピュータとして議論されるものの中には、量子アニーリング方式などもあります。
量子コンピュータが人工知能を加速するには量子アニーリングコンピュータをクラスタリングやニューラルネットワーク、そしてボルツマンマシンなどに使うことができるという議論がありました。
機械学習の学習プロセスの多くは最適化問題と捉えることができるので、これは面白いアプローチです。しかしだんだん疲れてきましたし、こちらについては参考文献が見つかりやすいと思いますのでまたにします。
ちなみにDeep Learningは計算量が多く、大量に電力を消費します。これが電力消費の効率化に向けた進化を要請してもいます。
そして量子コンピュータの消費電力はとっても低いのです。
(もちろん電力の最適化も量子アニーリングコンピュータやAIがやってくれるんでしょう!)
人工知能に対するDeep Learningとは違ったタイプのアプローチ
私見、かつ広く受け入れられている話だと思いますが、Deep Learning関係の機械学習のアプローチ(主にCCN含むfeed-forwardと、LSTMを含むrecurrentのコンビネーションといったもの)には一般的な知性に向けたアプローチとして限界を感じます。
前述した、本質的な教師なし学習という意味においてもですし、データと時間がかかりすぎるという点もよく指摘されますが、それよりも、演繹的知性という観点においてどうしても何かが足りないと感じてしまいます。演繹的な知性と帰納的な知性の差は決定的で、人工生命的な全く違うアプローチが求められているのでは?と思います。
(…と書きながら思いましたが、もしかしたら本質的な教師なし学習、データと時間の問題、演繹的知性といったものは全て違う仮面を被った同じ問題なのかもしれません)
それにどう繋がるか自明ではありませんが、Deep Learningとは全く違うタイプの取り組みとして、例えば私の働くオフィスの真隣に、Blue Brain Projectの拠点があります。

ここはComputational Neuroscienceの一大拠点で、Blue Brain Projectは人間の脳全体のコンピュータシミュレーションを最終的には分子レベルで構築することを目標としたプロジェクトです。
Goodfellow博士のテキストにもありますが、Computational NeuroscienceはDeep Learningとは全く違う分野で、Deep Learningはとあるタスクを処理するためのコンピュータシステムを作ることが目的といった応用分野という意味合いが強い一方、Computational Neuroscienceは脳が実際のところどのような処理をしているかという正確なモデルを作るのが目的の分野です。
ただ、人材交流は盛んなようで、Blue Brainの中で私が一番仲の良い研究者はスタンフォードで機械学習をやっていたアメリカ人で、Hodgkin–Huxley modelに基づいたニューロンのシミュレーションを営々と行っています。
ちなみにシミュレーションに用いるソフトはオンラインで公開されているので、ご興味があれば自分のコンピュータで走らせることもできます。
より発生的なアプローチとして、人工生命という分野もあります。
Overviewを掴むためにArtificial Lifeを含む関連記事を特徴語でざっくりクラスタリングしてみたところ、トップレベルでは1)機械学習/Deep Learningの応用や関連、2)生物学寄りのもの、そして3)創発・複雑系領域、と大きく3つくらいのクラスタがありそうです。

この中で創発・複雑系領域の研究は少なくとも80年代からあちこちで行われており、私の興味は基本的にここにあります。(これは多感なteen時代に(例にもれず)ミッチェル・ワールドロップの「複雑系」/ "Complexity"の直撃を受けた影響が大きいです。hypeとも評価されますが…)
ただし創発・複雑系研究とDeep Learningは歴史的には親戚のような関係もあって、ニューラルネットワークも大元は複雑系のMulti Agent Simulationに近いアプローチから生まれたような所があるのだと思います。(※その時代を生きていないので想像です)
着想としては、シンプルなユニットも集まれば知的な振る舞いをするという創発的な考え方で、これはdistributed representationなど今も通用する考え方に繋がるとも言われます。あるいは計算ユニットを繋いでインタラクトさせるだけで知能を再現しようとすると言ってもいいかもしれません。
私もconnectionismを最発明をしているだけではないかと思いつつ学習する複雑系シミュレーションをあれこれと試したりしているのですが、しかしデジタルコンピュータの計算量の限界を感じます。
特に複雑系研究は多数のAgentを用いたシミュレーションを行うので、デジタルコンピュータ(つまり普通のコンピュータ)でシミュレーションを行おうとすると、Agentの数が増えるとステップ毎の計算量が指数的に増加して手に負えなくなるのです。
BlockchainやDeep Learningが古典的コンピュータと違うオーダーの計算力を量子コンピュータに対して要請するように、人工生命研究も計算力を要請していると感じます。
その中で、アナログコンピュータが議論されることもあります。
複雑系研究においてシミュレーションと実験は色々な意味で異なります。例えば、デジタルコンピュータを用いるシミュレーションと比べて、自然界は物理法則を圧倒的に高速で演算してくれるアナログコンピュータという点で素晴らしいものです。
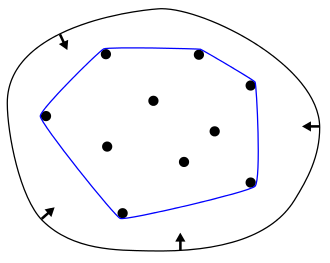
このアナログ計算の概念を示すものとして、例えばスパゲッティをソートすべき数値の集まりとみなしたり(集合の各要素の値に対応する長さのスパゲッティで束をつくり、筒に入れて机に立ててトントンと揃えると、ソートが完了する)、輪ゴムを点の集合の凸包を探すのに使ったり(下図1)、シャボン膜を極小曲面を求めるのに使ったりといったことが挙げられます。(下図2)

最小表面積の計算: シャボン膜は物理法則に従い最小表面積で張りますが、コンピュータでこの膜形状を求める計算を行うのは簡単ではありません。
もちろん実際の実験はうまくいかなくてムカつくことも多いけど、それもまた自然法則…
しかし量子コンピュータ、特にアニーリング的なコンピュータはアナログ的なところがありますよね。
人工知能とブロックチェーンについて
これはちょっと違ったカラーの項目になりそうだし存外深くなりそうな気がするので、また今度気が向いたら。
まとめ
人工知能は古典デジタルコンピュータの計算力増大とデータ量の増大に伴い、Deep Learningで素晴らしいパフォーマンスを出してブームに乗っています。メディアも「人間レベルを超えた」等と囃し立てますし、投資額も巨大です。
しかしDeep Learningとは別のアプローチも数多くあり、研究を続けている人は多くいます。人工生命に近いアプローチも根強くあります。
それらの技術は広義の量子コンピュータ技術の進化を要請します。
そして(特に狭義の)量子コンピュータの進化は、こちらも進化と多様化を続ける広義のBlockchain、そしてそのベース技術にも影響を与え、お互いの進化を促します。
何かの技術が絶滅した時には、ニッチを埋めるような戦略を取る新たな技術が誕生して生態系の中で賢く生きて行くかもしれません。
生命の進化のように、多くの技術は何かの閾値を超えるとどっと多様化し、何かのきっかけで大絶滅した後は、生き残った適者がインクリメンタルな適応進化をする、という現象を見せるのかもしれません。
生命としての人類の進化について、技術の進化も統合する形で今年もも考えて行きたいです。
色々盛り込んだ結果、専門ではない領域についての言及が殆どになりました。
雰囲気だけで正しくなかったり、最新情報をキャッチアップできていなかったりすると思いますので、各方面から飛んでくるマサカリをお待ちしています。
(謙虚に努力しますので、できれば思いやりをもって投げて頂けると嬉しいです)