IBMが (いわゆるゲート方式/回路型の) 量子コンピュータを利用できる環境を提供しているので試してみました。
環境は
- Python 3.5
- Anaconda 5.01
- QISKit ("pip install qiskit") / https://github.com/QISKit/qiskit-sdk-py
- QISKitは、深さが限定的な量子回路を設計して直近の応用を意識した量子コンピューターのアプリケーションを開発したり 実験を行うためのソフトウェア開発キットです。
公式が提供しているIBM Qや量子コンピュータについての情報はこちら
https://www.research.ibm.com/ibm-q/learn/
イントロダクション
量子コンピュータでは、0か1の状態を取るbitではなく、同時に0と1の状態を取れるqubitを使います。
この0と1の重ね合わせ状態を利用し、n個のqubitがあれば、2^n個の状態を同時に計算できます。
また、量子もつれ/entanglementという現象を工夫・利用したアルゴリズムを使うことで結果的に高速に計算を行うことができます。
参考 > 高速化の鍵は量子の「もつれ」や「重ね合わせ」ーー 量子コンピューターの原理を知る
2017年末にIBMは50 qubitsのプロトタイプを作ったと発表しましたが、現在20 qubitsまでが商用利用できるようです。
5 qubitsのマシンはこれから紹介するComposer上から無料で使えます。
量子コンピュータ実機のナリ
こんな感じです。
実際はこの写真の装置の下の方にもう少し小さい筒上の装置がついていて、その中に小さなチップがあります。そこにqubitsが作られます。
装置全体は絶対零度近くまで冷却され、特に下部のチップのある場所は0.01Kくらいまで冷却されます。
たぶんこの辺だと思いますが、間違ってたらすみません。
環境・使い方
まずはこちらから利用登録
https://quantumexperience.ng.bluemix.net/qx/signup
登録後、ログインしてComposerタブにいくと使えるマシンのリストを見ることができます。
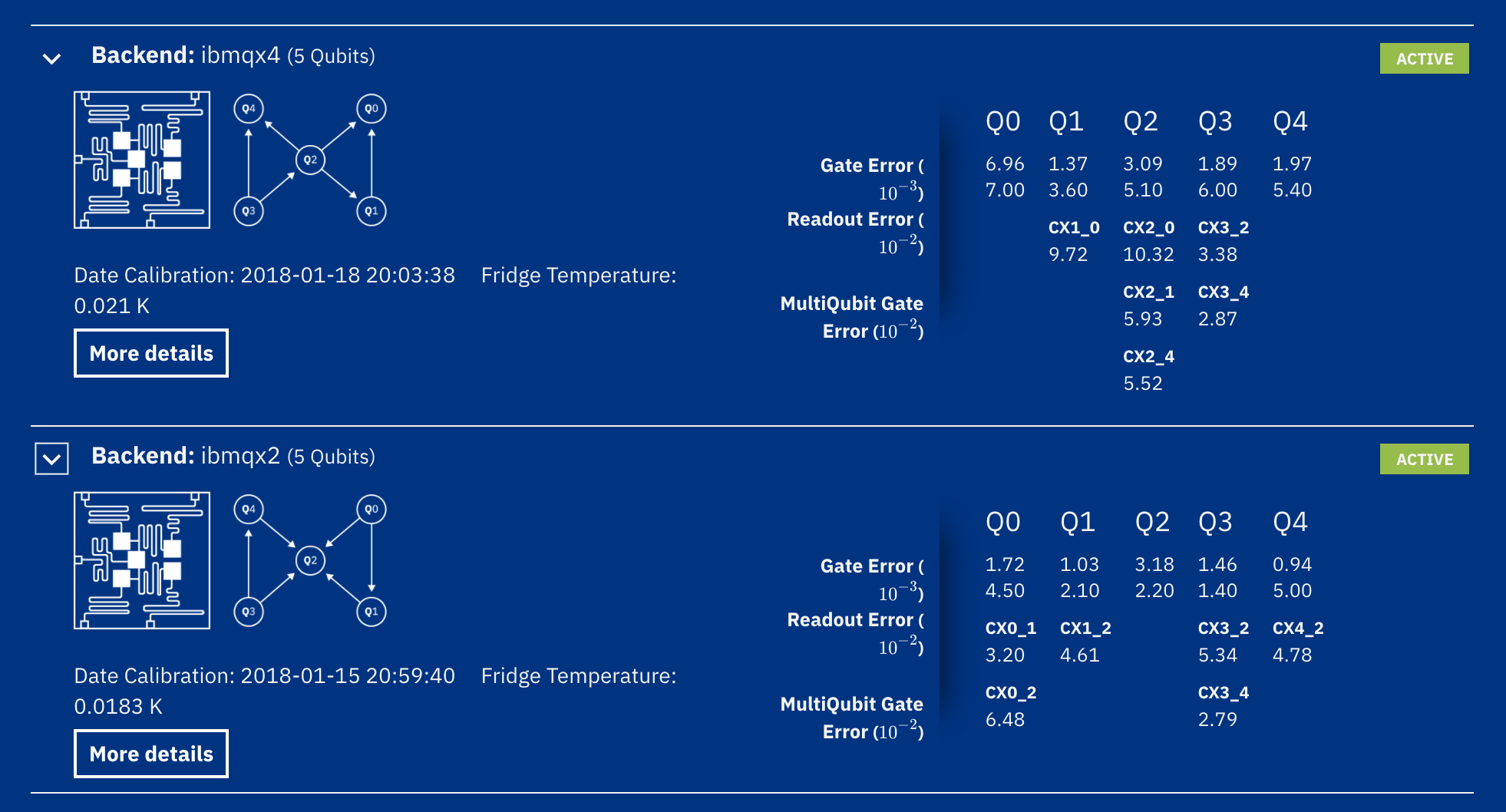
5 qubitsのマシンがふたつ使えるのがわかります。
ここでq0からq4までのqubits同士をつなぐ矢印をみると、qubitの全て同士がentanglement状態にできる訳ではないことがわかります。
上のibmqx4では、q0はq1ないしq2とentanglement状態を作り、q1ないしq2の状態や観測によってq0の状態を変化・確定することができますが、q3, q4とそういった関係を作ることはできません。
下の方にスクロールすると、こういうインターフェースがあります。
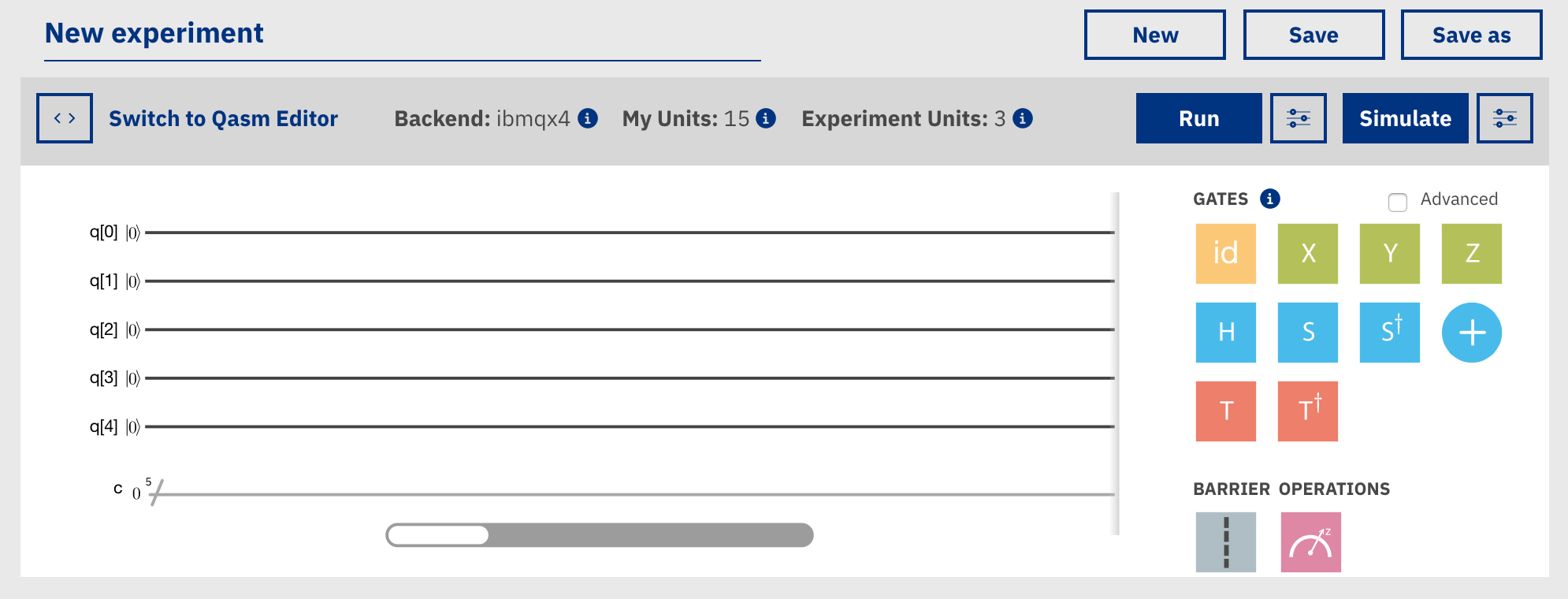
この5本線の上に、右側からGate (演算子) をドラッグすることで、5つのqubitを制御・観測できます。
q0からq4までの5つのqubitは5本線の一番左で |0〉に初期化されます。
プログラムの実行（実験）は右側に向かって進んでいきます。
Gateを配置したら、Runを押して実際にリモートでIBMの量子コンピュータを走らせることもできますし、Simulateを押して(実物を動かさずに)シミュレート結果を見ることもできます。
しかし、実際にRunで走らせると実験装置や計測の不完全性により誤差が発生します。
たとえば以下のように、
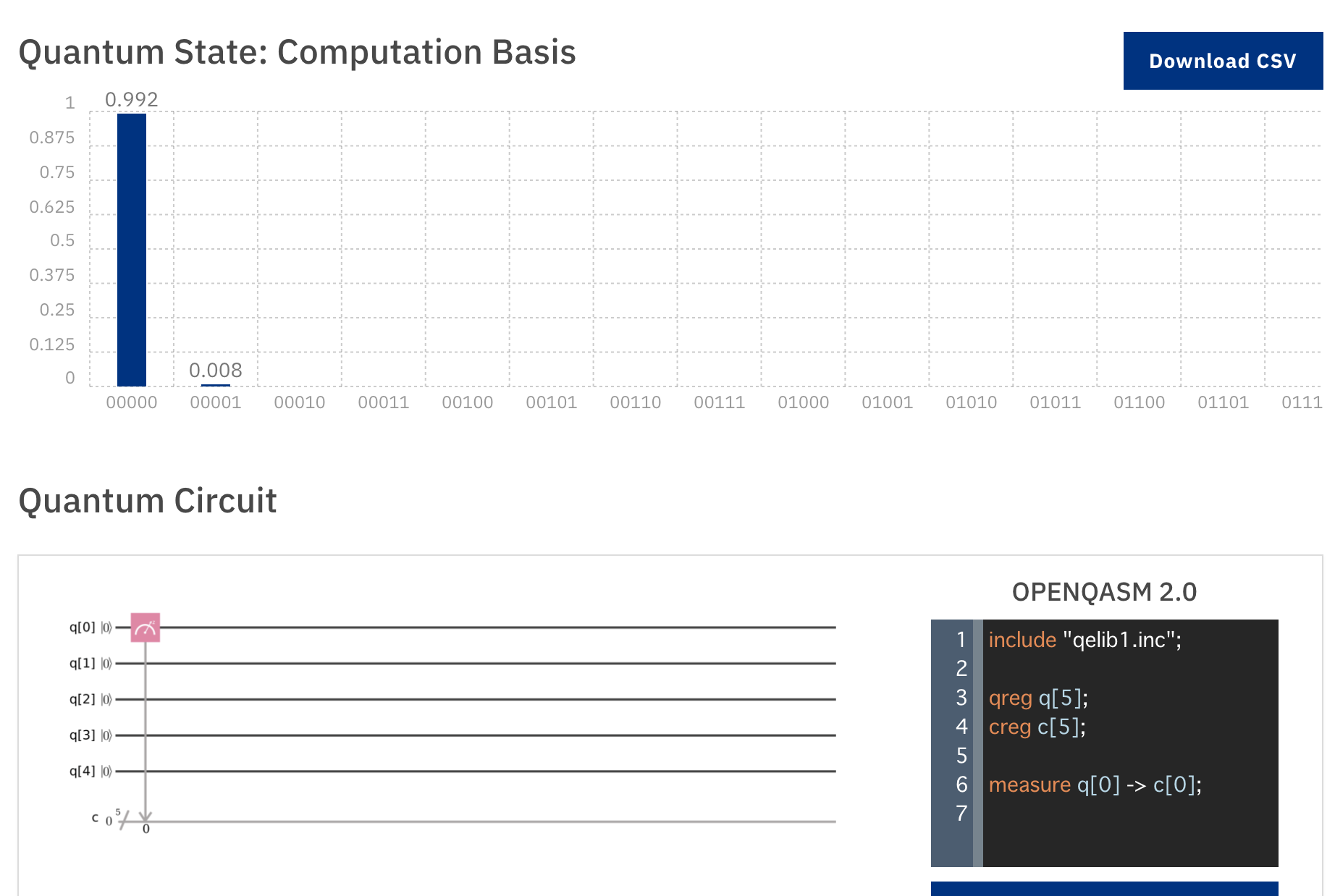
|0〉に初期化したqubitの状態を単純に計測しようとしても確実にq0 = 0と観測はされず、0.992という結果になりました。
Simulationで実行すると完全に1.000の確率でq0 = 0という結果になります。
また、実機を動かしたい時に、すでに同じ構成のプログラム（実験）が過去に走っていればキャッシュから実行結果を見ることができます。
実際に実機を動かしたければ、New Executionを進めましょう。混み具合にもよりますが、数十分から数時間後に実行され、結果がメールで届きます。
Simulationでもやりながら気長に待ちましょう。
ゲートの紹介と、基本的な使い方、ベーシックな理解
では、実際にいろいろゲートを使ってみましょう。
Hadamard Gate
Hゲートはqubitを z 軸と x 軸の間の軸を中心に 180°回転させます。
この操作により、$ |0\rangle $ は $ \frac{|0\rangle + |1\rangle}{\sqrt{2}} $ に、 $ |1\rangle $ は $ \frac{|0\rangle - |1\rangle}{\sqrt{2}}$ に変換されます。
つまり、 |0〉 を、 |0〉と |1〉が均等に混ざった状態に変換できます。
ノイズは無視できませんが、大雑把に言えば50:50の結果となりました。
Hadamard変換を2回行ってみる
折角なので、ちょっと量子コンピュータっぽい演算をやってみましょう。
上記のHadamard変換を2回行うとどうなるでしょうか？
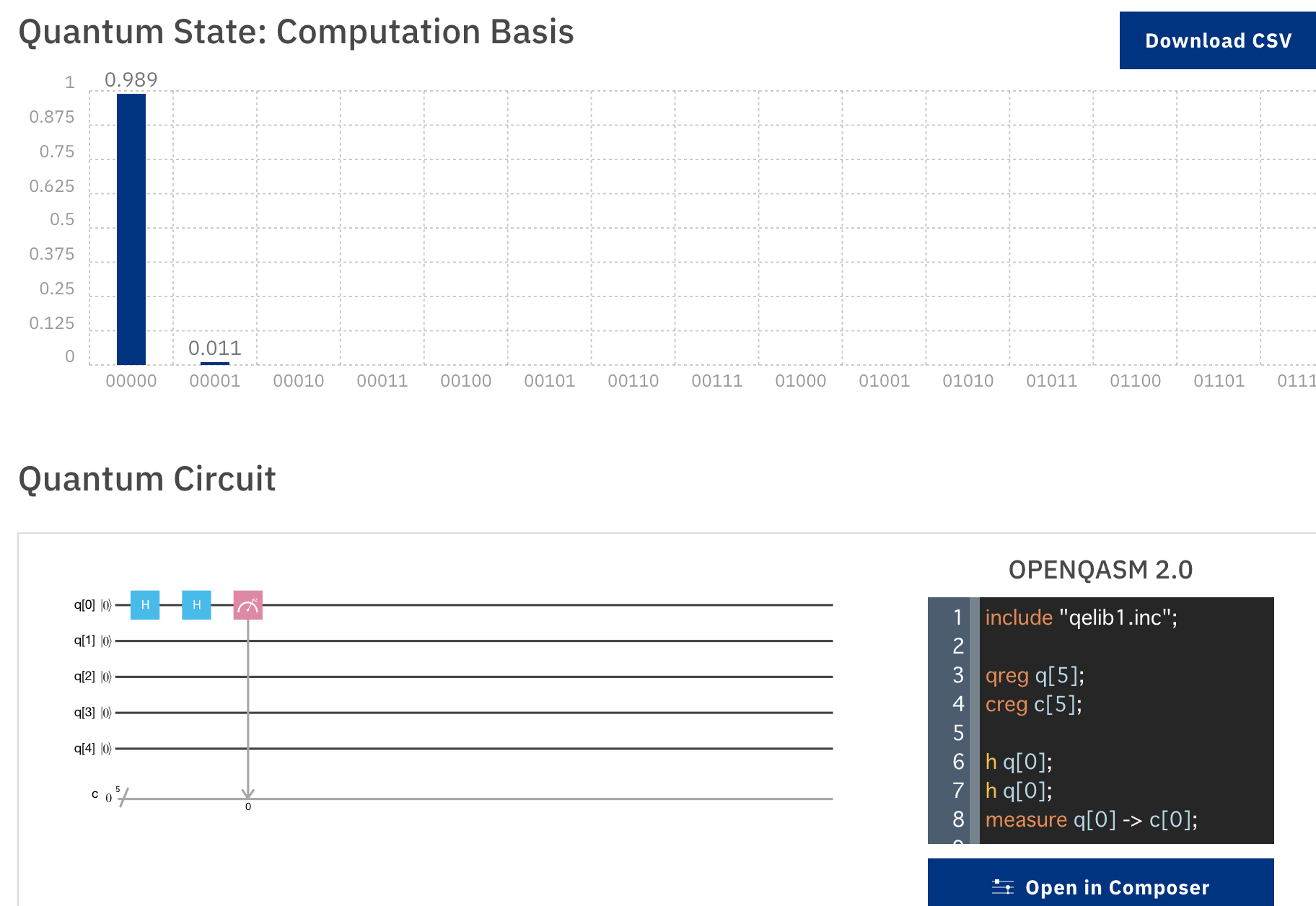
結果はほぼ 0と観測されました。
Hadamard変換によると |1〉 も |0〉と |1〉が均等に混ざった状態に変換されるので、上の結果（0と1が半々）に対してHadamard変換をかけても 0 or 1が均等に観測されるのでは？ というとそうではなく、 $ |0\rangle $ が $ \frac{|0\rangle + |1\rangle}{\sqrt{2}} $ に変化して、 $ |1\rangle $ が $ \frac{|0\rangle - |1\rangle}{\sqrt{2}}$ に変化するため、$ \frac{|0\rangle + |1\rangle}{\sqrt{2}} $ の重ね合わせ状態にHadamard変換が行われると、|0〉の確率振幅は同じ符号のため増幅する一方で、|1〉の確率振幅は確率振幅が異なる符号のため干渉で打ち消し合います。
180度回転したqubitが再び同軸を中心に180度回転するので元に戻ると考えるとわかりやすいかもしれません。
結果、観測されるのは |0〉となります。
Controlled NOT Gate
今度は続いて、2つのqubitを繋ぎ、entanglementを試してみましょう。
制御NOTゲート ( Quantum Composerでは +マークの演算子) はcontrolとtargetの2つのqubitを持ち、controlが1の時のみtargetのビットを反転します。
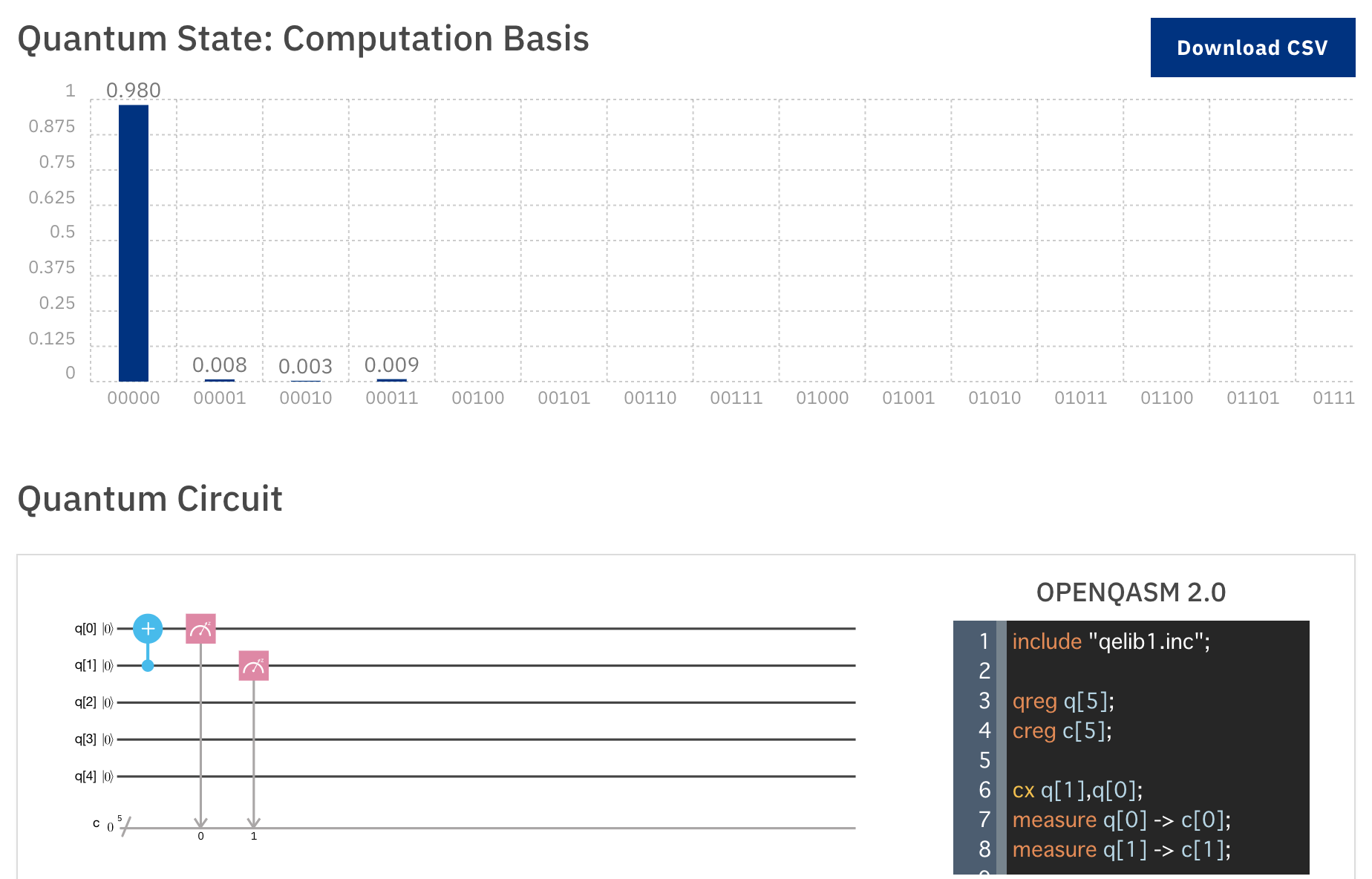
ここではq1がcontrol, q0がtargetです。
q1が |0〉のため、q0は反転されず、q0, q1ともに |0〉となります。
パウリXゲート
パウリXゲートはビット反転演算子で、 |0〉を |1〉にします。
これを一つ前の実験に加えてみましょう。
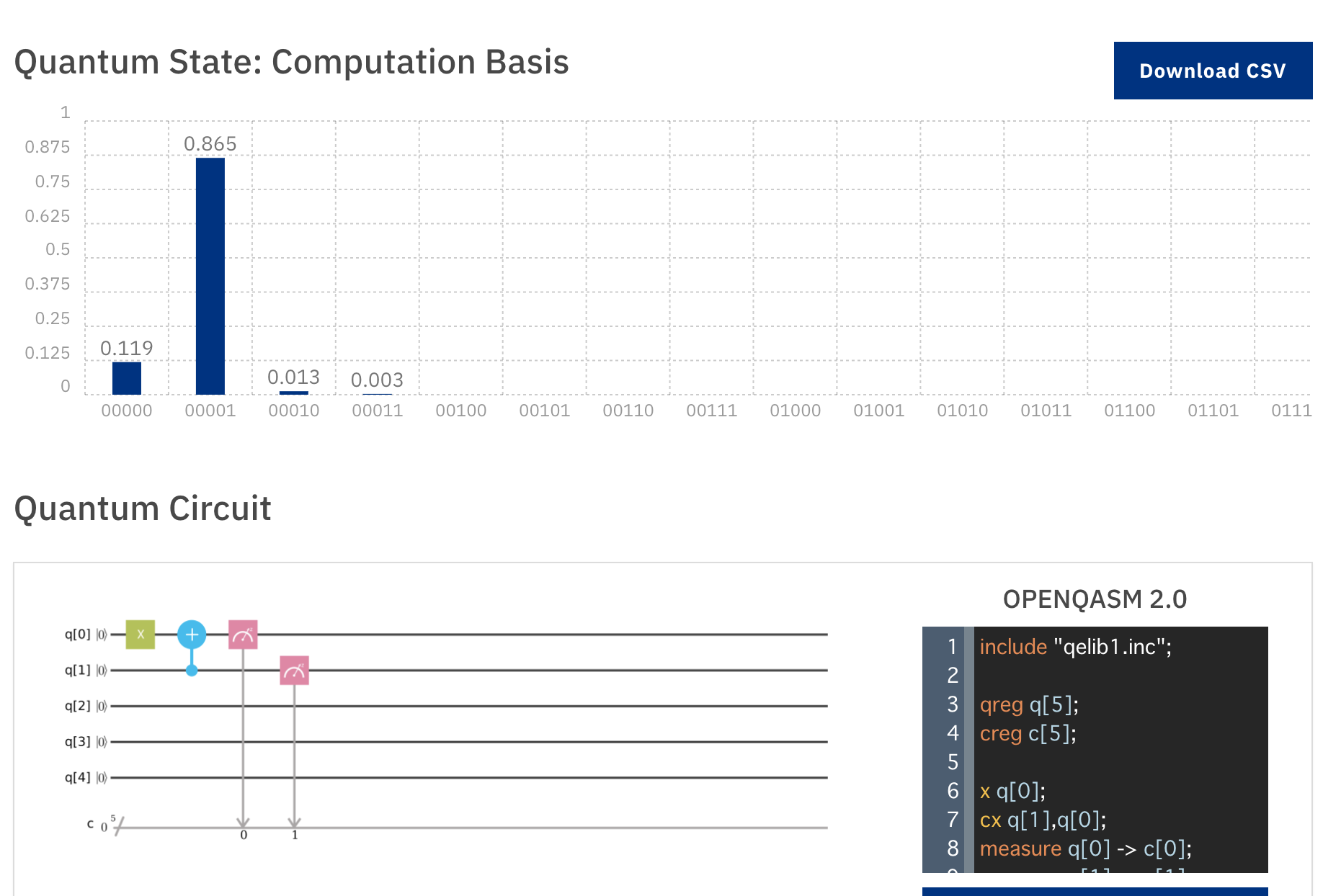
相変わらずq0はq1によってコントロールされていますが、q1が |0〉のためq0は影響を受けません。
|0〉に初期化されたものがXゲートで |1〉になり、それがそのまま観測されます。
Xを移動させてみる
|0〉に初期化されたq1はXゲートを通って |1〉になります。
結果、q0はq1で上書きされ、|1〉となります。
ここまでの結果を見てみると、プログラムが長くなるとエラーが大きくなるのがわかります。
時間がたつとqubitの最初の状態が壊れていくからです。
このノイズ（エラー）を減らすのは量子コンピュータの研究開発における大きなチャレンジです。
XゲートをHadamardゲートに置き換えると
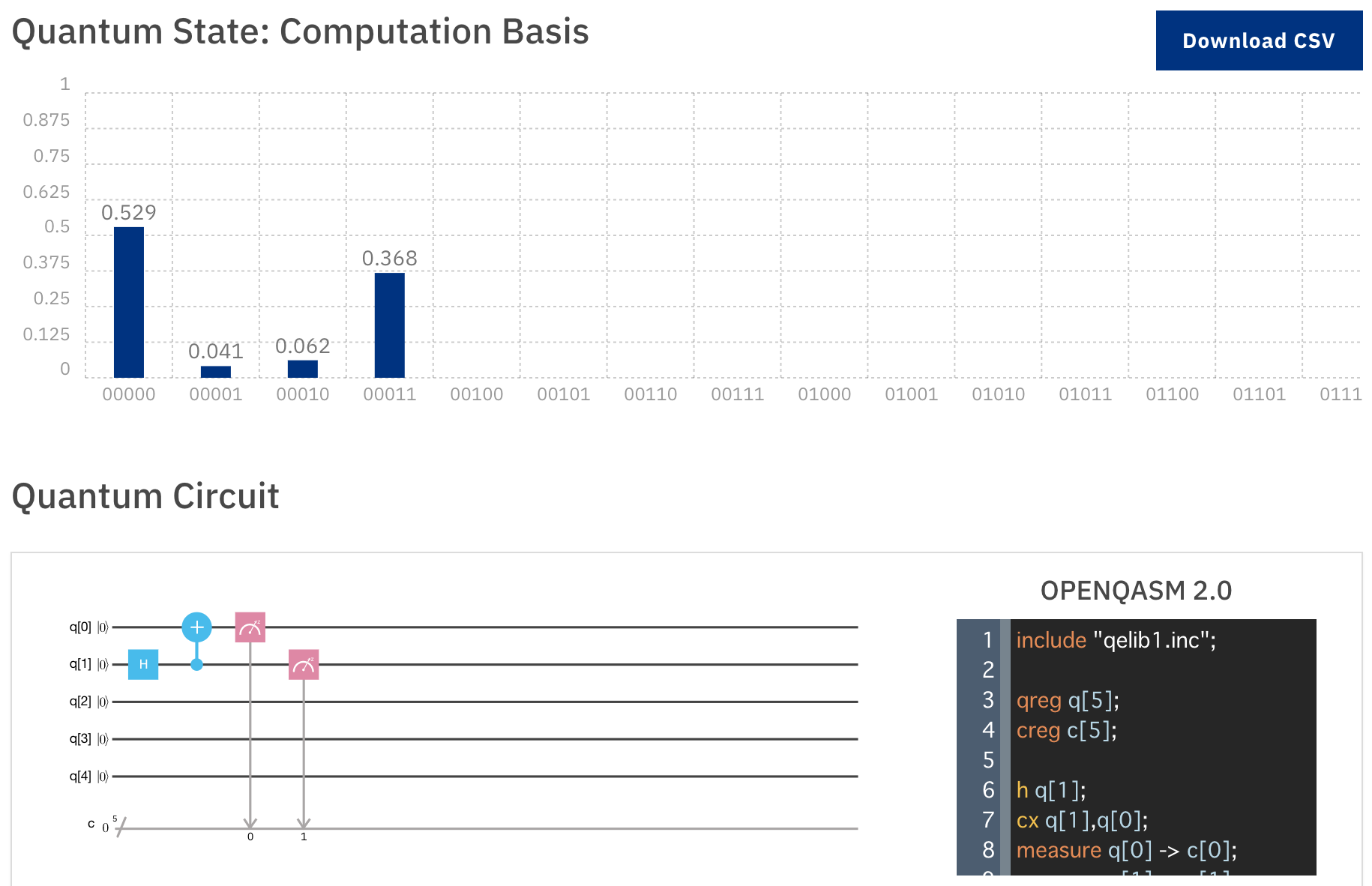こうなります。
q1がおよそ0.5の確率で |0〉か |1〉となり、それによってq0がおよそ0.5の確率で反転されます。
その他のGate
その他、Z軸まわりに90度回転させるSゲート、同じく45度回転させるTゲート、Y軸周りに回転させるYゲートなどもあります。
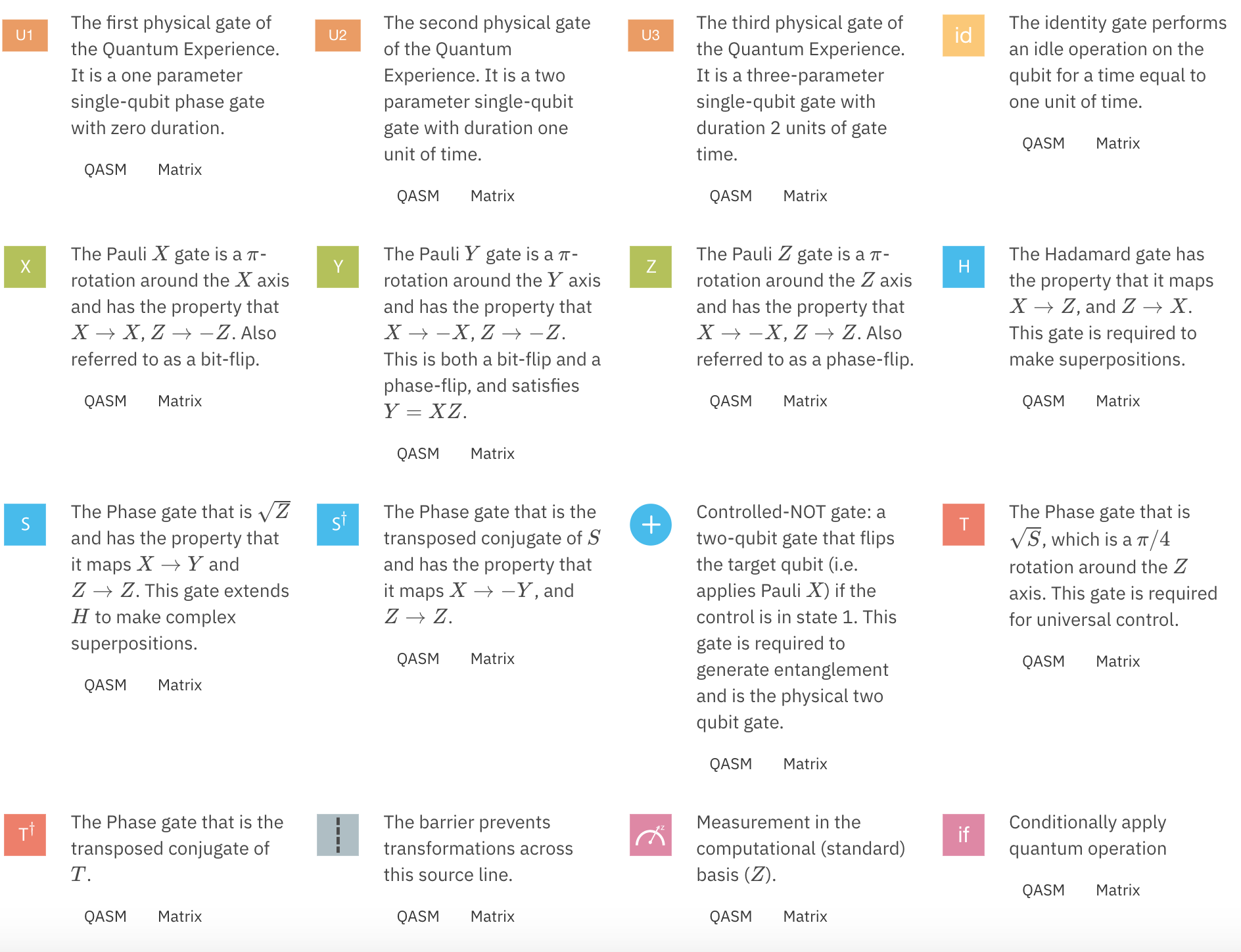
各ゲートについて学びつつも、実際に繰り返し使って結果を見て理解していくことが近道だと思います。
その際は、RunではなくSimulationを使った方がノイズに惑わされず理解が捗ると思います。
マメ知識
観測されたqubitは 0 か 1 という値を取りますが、その後qubitの情報は古典的なbitになります。これは、重ね合わせやentanglementの量子特性を失うことを意味しています。
QISKit
Quantum Composerは量子コンピュータの挙動を理解するにはとってもいいイントロですが、ハイレベルな実装に進むには限界があります。
そこで、QISKitを使います。
という訳で、気が向けばQISKit編に続きます…