概要
自然言語処理について勉強を始めたい人へ、簡単な理論から実験コードまで載せています。
実行環境はJupyter notebookやGoogle Colaboratoryなんかを想定しています。
キーワード:分散表現, BoW, Word2Vec, CBoW, skip-gram
目次
分散表現
コンピュータに人間の言語(自然言語)を扱わせる上で必須となるのが分散表現です。
もちろんですがコンピュータは数値しか取り扱うことができないため、自然言語を何らかの形で数値に変換する必要があります。また、変換する際は変換元の単語をできる限り復元可能な形で変換する必要があります。
変換の方法としては単語をベクトルとして表す方法があり、そうして得られたベクトルを分散表現と言います。このベクトルは大抵100〜300次元で表されており、もちろん次元が大きいほど表現力が高くなりますが、その分メモリや計算コストを多く必要とします。
具体例で考えてみます。
例えば
自然 言語 処理 に ついて 勉強 する 。
という語彙しか存在しない言語を考えます。この場合なら7単語しかないため、この7単語についてそれぞれ
\begin{array}
a自然 &= (1, 0, 0, 0, 0, 0, 0) \\
言語 &= (0, 1, 0, 0, 0, 0, 0) \\
処理 &= (0, 0, 1, 0, 0, 0, 0) \\
に &= (0, 0, 0, 1, 0, 0, 0) \\
ついて &= (0, 0, 0, 0, 1, 0, 0) \\
勉強 &= (0, 0, 0, 0, 0, 1, 0) \\
する &= (0, 0, 0, 0, 0, 0, 1)
\end{array}
といった感じに7次元のベクトルを割り振ると完全に分離された分散表現が得られます。(one-hot表現)
他にも2進数を割り振れば
\begin{array}
a自然 &= (0, 0, 1) \\
言語 &= (0, 1, 0) \\
処理 &= (0, 1, 1) \\
に &= (1, 0, 0) \\
ついて &= (1, 0, 1) \\
勉強 &= (1, 1, 0) \\
する &= (1, 1, 1)
\end{array}
のように3次元のベクトルで分散表現を作成することもできます。
このように、分散表現自体は好きな方法で構築することができますが、上記の分散表現は両方とも利便性の観点から問題があります。
1つ目の分散表現の問題は単純に語彙数に比例してベクトルの次元も大きくなってしまうことです。先の例だとたった7単語しかありませんでしたので全く問題ありませんが、現実では何万何十万という語彙があるため、1つ目のようなやり方ではあっという間にとんでもない量のメモリを食うことになってしまいます。
その点2つ目のやり方だと$2^{20}=1048576$なので、たった20次元で約100万単語に対して一意のベクトルを生成することができます。が、こちらにも問題があります。
それは、分散表現を利用した自然言語処理を行う上で非常に不便、というより利用できないということです。一意のベクトルを作成することができても、それではただ単に各単語にラベルを付けただけであり、単語間の関連や共起性1、意味、役割...といった情報が一切含まれていません。
そのため、ただ単に単語がベクトルになっただけで何もわからない、という状況になってしまいます。この問題は1つ目のやり方でも同様に存在しています。
Bag of Words
ここまでで挙がった分散表現を作る際の課題をまとめると、
- いかに表現力を維持しつつ次元数を抑えるか
- いかに単語間の関連や共起性、意味、役割などの情報を含めるか
といった感じです。
これらの課題を解決する分散表現の作成方法のうち、ディープラーニング登場以前によく使われていたのがBoW: Bag of Wordsです。
BoWは単語の出現頻度に着目して分散表現を作成する方法で、単語間の関連や意味、役割などは考えませんが共起性は取り込むことができます。
例えば
私 は ラーメン が 好き だ 。
私 は 寿司 が 好き だ 。
彼 は ラーメン が 好き だ 。
という文章をBoWで表現すると、
| 。 | が | だ | は | ラーメン | 好き | 寿司 | 彼 | 私 | |
|---|---|---|---|---|---|---|---|---|---|
| 文章1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 文章2 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 文章3 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
のようになります。単語が出現していれば1、そうでなければ0としています。
ちなみにBoWの分散表現の作り方はいろいろあるため、これはあくまで一例であることに注意してください。
from sklearn.feature_extraction.text import CountVectorizer
corpus = ["私 は ラーメン が 好き だ 。",
"私 は 寿司 が 好き だ 。",
"彼 は ラーメン が 好き だ 。"]
def tokenizer(text):
return text.split(" ")
cv = CountVectorizer(tokenizer=tokenizer)
weights = cv.fit_transform(corpus)
print(cv.get_feature_names())
print(weights.toarray())
['。', 'が', 'だ', 'は', 'ラーメン', '好き', '寿司', '彼', '私']
[[1 1 1 1 1 1 0 0 1]
[1 1 1 1 0 1 1 0 1]
[1 1 1 1 1 1 0 1 0]]
これにより文章のベクトルが作成できたので、文章の類似度を計算することができます。例えばよく使用されるcos類似度で3つの文章の類似度を計算してみます。
from sklearn.metrics.pairwise import cosine_similarity
x = weights.toarray()
sim = cosine_similarity(x)
for i in range(len(x)):
for j in range(i+1, len(x)):
print(f"文章{i+1}と文章{j+1}の類似度:{sim[i, j]}")
文章1と文章2の類似度:0.8571428571428569
文章1と文章3の類似度:0.8571428571428569
文章2と文章3の類似度:0.7142857142857141
続いて単語の分散表現に移ります。単語の分散表現を作るには、「単語の意味は周辺の単語によって形成される」という分布仮説をもとに共起行列を作る方法があります。
| 。 | が | だ | は | ラーメン | 好き | 寿司 | 彼 | 私 | |
|---|---|---|---|---|---|---|---|---|---|
| 。 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| が | 0 | 0 | 0 | 0 | 2 | 3 | 1 | 0 | 0 |
| だ | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 |
| は | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 1 | 2 |
| ラーメン | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| 好き | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 寿司 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 彼 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 私 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
vocab = cv.get_feature_names()
n_vocab = len(vocab)
w2id = dict(zip(vocab, range(n_vocab)))
id2w = dict(zip(range(n_vocab), vocab))
window_size = 1
cooccurrence = np.zeros((n_vocab, n_vocab), dtype=int)
for text in corpus:
split_text = tokenizer(text)
for i, word in enumerate(split_text):
for j in range(1, window_size+1):
if i - j >= 0:
cooccurrence[w2id[word], w2id[split_text[i-j]]] += 1
if i + j < len(split_text):
cooccurrence[w2id[word], w2id[split_text[i+j]]] += 1
cooccurrence
[[0 0 3 0 0 0 0 0 0]
[0 0 0 0 2 3 1 0 0]
[3 0 0 0 0 3 0 0 0]
[0 0 0 0 2 0 1 1 2]
[0 2 0 2 0 0 0 0 0]
[0 3 3 0 0 0 0 0 0]
[0 1 0 1 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0]
[0 0 0 2 0 0 0 0 0]]
コーパス2が文章3つしかないため酷い精度ですが、一応これで単語の共起行列が生成できました。
これをもとに単語間の類似度を計算してみます。
sim = cosine_similarity(cooccurrence)
for i in range(n_vocab):
for j in range(i+1, n_vocab):
print(f"「{id2w[i]}」と「{id2w[j]}」の類似度:{sim[i, j]}")
「。」と「が」の類似度:0.0
「。」と「だ」の類似度:0.0
「。」と「は」の類似度:0.0
「。」と「ラーメン」の類似度:0.0
「。」と「好き」の類似度:0.7071067811865476
「。」と「寿司」の類似度:0.0
「。」と「彼」の類似度:0.0
「。」と「私」の類似度:0.0
「が」と「だ」の類似度:0.5669467095138409
「が」と「は」の類似度:0.42257712736425834
「が」と「ラーメン」の類似度:0.0
「が」と「好き」の類似度:0.0
「が」と「寿司」の類似度:0.0
「が」と「彼」の類似度:0.0
「が」と「私」の類似度:0.0
「だ」と「は」の類似度:0.0
「だ」と「ラーメン」の類似度:0.0
「だ」と「好き」の類似度:0.0
「だ」と「寿司」の類似度:0.0
「だ」と「彼」の類似度:0.0
「だ」と「私」の類似度:0.0
「は」と「ラーメン」の類似度:0.0
「は」と「好き」の類似度:0.0
「は」と「寿司」の類似度:0.0
「は」と「彼」の類似度:0.0
「は」と「私」の類似度:0.0
「ラーメン」と「好き」の類似度:0.5
「ラーメン」と「寿司」の類似度:0.9999999999999998
「ラーメン」と「彼」の類似度:0.7071067811865475
「ラーメン」と「私」の類似度:0.7071067811865475
「好き」と「寿司」の類似度:0.5
「好き」と「彼」の類似度:0.0
「好き」と「私」の類似度:0.0
「寿司」と「彼」の類似度:0.7071067811865475
「寿司」と「私」の類似度:0.7071067811865475
「彼」と「私」の類似度:1.0
これだけ小さなコーパスで、適当すぎる文章から生成した共起行列ですが、それでも助詞同士や主語同士、目的語同士の類似度は高く見積もられていますね。もっと大きなコーパスで試せば良い精度が得られそうな感じがします。
次元削減
ところでこの共起行列ですが、当然ながら語彙量が増えるとそれに比例して各単語ベクトルのサイズが大きくなります。語彙量は簡単に数万になりますので、このままではとても扱いきれません。
それに、先の例の共起行列を見ていただけるとわかるとおりほとんどの要素がゼロとなっており無駄が多いです。
そのため、次元圧縮という方法で単語ベクトルのサイズを削減することが一般的です。
次元圧縮の方法はPCA:主成分分析やSVD:特異値分解などがあります。
今回は特にSVDについて、実際に先の例の共起行列で試してみましょう。理論面なんかは全て参考に譲ります。
import numpy as np
np.set_printoptions(linewidth=200)
u, s, vh = np.linalg.svd(cooccurrence, full_matrices=False)
print("----- u -----")
print(u)
print("----- s -----")
print(s)
print("----- vh -----")
print(vh)
----- u -----
[[ 0.00000000e+00 4.34792206e-01 0.00000000e+00 4.40054003e-01 6.62372089e-01 0.00000000e+00 -4.22577127e-01 -8.27511384e-17 -8.30537873e-33]
[-6.44504833e-01 0.00000000e+00 3.34129985e-01 0.00000000e+00 0.00000000e+00 -6.87728634e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[-7.37140310e-01 0.00000000e+00 -5.10421773e-01 0.00000000e+00 0.00000000e+00 4.42824769e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[-2.03070635e-01 0.00000000e+00 7.92355202e-01 0.00000000e+00 0.00000000e+00 5.75269980e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00]
[ 0.00000000e+00 3.33287257e-01 0.00000000e+00 -6.47457118e-01 -1.12142889e-01 0.00000000e+00 -5.07092553e-01 -4.47213595e-01 5.63262098e-18]
[ 0.00000000e+00 8.14944633e-01 0.00000000e+00 1.51987849e-01 -3.66324324e-01 0.00000000e+00 4.22577127e-01 5.55111512e-17 8.47409176e-33]
[ 0.00000000e+00 1.66643628e-01 0.00000000e+00 -3.23728559e-01 -5.60714443e-02 0.00000000e+00 -2.53546276e-01 8.94427191e-01 -1.12652420e-17]
[ 0.00000000e+00 3.99261526e-02 0.00000000e+00 -2.27706508e-01 2.86827360e-01 0.00000000e+00 2.53546276e-01 2.27905073e-16 -8.94427191e-01]
[ 0.00000000e+00 7.98523052e-02 0.00000000e+00 -4.55413016e-01 5.73654720e-01 0.00000000e+00 5.07092553e-01 1.17209363e-17 4.47213595e-01]]
----- s -----
[ 5.08615587e+00 5.08615587e+00 3.47972138e+00 3.47972138e+00 2.00563147e+00 2.00563147e+00 1.40746457e-16 2.73691106e-48 -0.00000000e+00]
----- vh -----
[[-4.34792206e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00 -3.33287257e-01 -8.14944633e-01 -1.66643628e-01 -3.99261526e-02 -7.98523052e-02]
[ 0.00000000e+00 6.44504833e-01 7.37140310e-01 2.03070635e-01 -1.20301362e-16 0.00000000e+00 -4.63952991e-18 7.22075342e-18 1.44415068e-17]
[-4.40054003e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00 6.47457118e-01 -1.51987849e-01 3.23728559e-01 2.27706508e-01 4.55413016e-01]
[-0.00000000e+00 -3.34129985e-01 5.10421773e-01 -7.92355202e-01 -4.67674202e-17 0.00000000e+00 -5.11392857e-17 -1.42277527e-17 -2.84555054e-17]
[-0.00000000e+00 -6.87728634e-01 4.42824769e-01 5.75269980e-01 -8.09271129e-18 0.00000000e+00 -3.18019313e-17 -2.96687350e-17 -5.93374699e-17]
[ 6.62372089e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00 -1.12142889e-01 -3.66324324e-01 -5.60714443e-02 2.86827360e-01 5.73654720e-01]
[ 0.00000000e+00 -3.70074342e-17 5.55111512e-17 7.44760246e-17 -4.47213595e-01 0.00000000e+00 8.94427191e-01 -1.33226763e-16 6.66133815e-17]
[ 0.00000000e+00 2.05432527e-33 -3.08148791e-33 0.00000000e+00 2.48253415e-17 0.00000000e+00 -4.96506831e-17 -8.94427191e-01 4.47213595e-01]
[-4.22577127e-01 0.00000000e+00 0.00000000e+00 0.00000000e+00 -5.07092553e-01 4.22577127e-01 -2.53546276e-01 2.53546276e-01 5.07092553e-01]]
ここで、$s$行列の要素が大きい6番目までで次元圧縮してみましょう。
compress_coocurrence = u[:, :6]@np.diag(s[:6])@vh[:6, :]
print(compress_coocurrence)
[[ 0.00000000e+00 -8.32044902e-16 3.00000000e+00 -5.57159782e-16 -3.48401238e-16 0.00000000e+00 -1.30815817e-16 -4.52324912e-17 -9.04649823e-17]
[ 4.88716010e-16 0.00000000e+00 0.00000000e+00 0.00000000e+00 2.00000000e+00 3.00000000e+00 1.00000000e+00 -1.55000252e-16 -3.10000504e-16]
[ 3.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00 -1.11962118e-16 3.00000000e+00 -5.59810591e-17 3.23287010e-17 6.46574020e-17]
[-8.87710888e-17 0.00000000e+00 0.00000000e+00 0.00000000e+00 2.00000000e+00 1.60417625e-16 1.00000000e+00 1.00000000e+00 2.00000000e+00]
[ 0.00000000e+00 2.00000000e+00 -1.40860966e-15 2.00000000e+00 -9.67431639e-17 0.00000000e+00 1.14503397e-16 5.09679842e-17 1.01935968e-16]
[ 0.00000000e+00 3.00000000e+00 3.00000000e+00 1.30734645e-16 -5.17429707e-16 0.00000000e+00 -2.29116128e-17 4.42028123e-17 8.84056246e-17]
[ 0.00000000e+00 1.00000000e+00 -6.05573384e-16 1.00000000e+00 -4.83715819e-17 0.00000000e+00 5.72516985e-17 2.54839921e-17 5.09679842e-17]
[ 0.00000000e+00 -9.30753913e-17 -5.44453816e-17 1.00000000e+00 7.97124080e-18 0.00000000e+00 2.12836304e-17 -4.32777572e-18 -8.65555144e-18]
[ 0.00000000e+00 -1.86150783e-16 -1.08890763e-16 2.00000000e+00 1.59424816e-17 0.00000000e+00 4.25672609e-17 -8.65555144e-18 -1.73111029e-17]]
圧縮前後の2乗誤差を比較してみましょう。
print(np.linalg.norm(cooccurrence - compress_coocurrence))
3.526933923021599e-15
この結果から分かる通り、圧縮の前後でほとんど情報が失われていませんね。
当然と言えば当然ですが、削減後の次元数が少ないほど元の共起行列とは異なるものになってしまうことに注意が必要です。
import matplotlib.pyplot as plt
diff = []
for i in range(1, n_vocab+1):
compress_coocurrence = u[:, :i]@np.diag(s[:i])@vh[:i, :]
diff.append(np.linalg.norm(cooccurrence - compress_coocurrence))
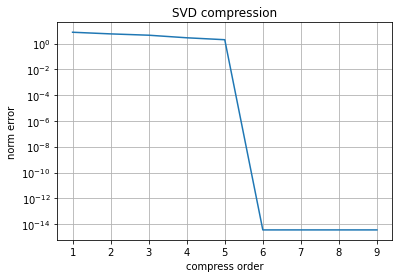
plt.title("SVD compression")
plt.yscale("log")
plt.plot(range(1, n_vocab+1), diff)
plt.grid()
plt.xlabel("compress order")
plt.ylabel("norm error")
plt.show()
グラフから、今回の場合は6次元までの圧縮では元の共起行列の情報をほとんど失わずに保持することができることがわかります。
これのどこが次元削減なのか、と思われる方もいらっしゃると思いますが、もちろんこのままでは次元削減できていません。というのも、SVDによる次元削減は特異値分解に付随するオマケだからです。
生成された$s$行列の各要素の大きさは重要度のようなものを表しており、ある程度の閾値でこれをカットすることで、可能な限り関係情報を維持したまま次元削減することができます。
print(u[:, :6]@np.diag(s[:6]))
[[ 0. 2.21142093 0. 1.53126532 1.32847431 0. ]
[-3.27805204 0. 1.16267925 0. 0. -1.37933019]
[-3.74921052 0. -1.77612555 0. 0. 0.88814329]
[-1.0328489 0. 2.75717533 0. 0. 1.15377958]
[ 0. 1.69515094 0. -2.25297037 -0.22491731 0. ]
[ 0. 4.14493543 0. 0.52887537 -0.73471159 0. ]
[ 0. 0.84757547 0. -1.12648519 -0.11245865 0. ]
[ 0. 0.20307064 0. -0.7923552 0.57526998 0. ]
[ 0. 0.40614127 0. -1.5847104 1.15053996 0. ]]
これで$9 \times 9$の共起行列が$9 \times 6$に削減されました。
実際に単語間の類似度を計算してみましょう。
sim = cosine_similarity(u[:, :6]@np.diag(s[:6]))
for i in range(n_vocab):
for j in range(i+1, n_vocab):
print(f"「{id2w[i]}」と「{id2w[j]}」の類似度:{sim[i, j]}")
「。」と「が」の類似度:0.0
「。」と「だ」の類似度:0.0
「。」と「は」の類似度:0.0
「。」と「ラーメン」の類似度:-9.358134352140677e-16
「。」と「好き」の類似度:0.7071067811865472
「。」と「寿司」の類似度:-8.309365609351454e-16
「。」と「彼」の類似度:-3.320011377892241e-16
「。」と「私」の類似度:-3.320011377892241e-16
「が」と「だ」の類似度:0.5669467095138412
「が」と「は」の類似度:0.4225771273642582
「が」と「ラーメン」の類似度:0.0
「が」と「好き」の類似度:0.0
「が」と「寿司」の類似度:0.0
「が」と「彼」の類似度:0.0
「が」と「私」の類似度:0.0
「だ」と「は」の類似度:1.2604230854720464e-16
「だ」と「ラーメン」の類似度:0.0
「だ」と「好き」の類似度:0.0
「だ」と「寿司」の類似度:0.0
「だ」と「彼」の類似度:0.0
「だ」と「私」の類似度:0.0
「は」と「ラーメン」の類似度:0.0
「は」と「好き」の類似度:0.0
「は」と「寿司」の類似度:0.0
「は」と「彼」の類似度:0.0
「は」と「私」の類似度:0.0
「ラーメン」と「好き」の類似度:0.49999999999999967
「ラーメン」と「寿司」の類似度:1.0
「ラーメン」と「彼」の類似度:0.7071067811865475
「ラーメン」と「私」の類似度:0.7071067811865475
「好き」と「寿司」の類似度:0.4999999999999998
「好き」と「彼」の類似度:-1.73340870411744e-16
「好き」と「私」の類似度:-1.73340870411744e-16
「寿司」と「彼」の類似度:0.7071067811865475
「寿司」と「私」の類似度:0.7071067811865475
「彼」と「私」の類似度:1.0000000000000002
比較してみると以下のようになります。
| 単語1 | 単語2 | 圧縮前の類似度 | 圧縮後の類似度 |
|---|---|---|---|
| 。 | が | 0.0 | 0.0 |
| 。 | だ | 0.0 | 0.0 |
| 。 | は | 0.0 | 0.0 |
| 。 | ラーメン | 0.0 | -9.358134352140677e-16 |
| 。 | 好き | 0.7071067811865476 | 0.7071067811865472 |
| 。 | 寿司 | 0.0 | -8.309365609351454e-16 |
| 。 | 彼 | 0.0 | -3.320011377892241e-16 |
| 。 | 私 | 0.0 | -3.320011377892241e-16 |
| が | だ | 0.5669467095138409 | 0.5669467095138412 |
| が | は | 0.42257712736425834 | 0.4225771273642582 |
| が | ラーメン | 0.0 | 0.0 |
| が | 好き | 0.0 | 0.0 |
| が | 寿司 | 0.0 | 0.0 |
| が | 彼 | 0.0 | 0.0 |
| が | 私 | 0.0 | 0.0 |
| だ | は | 0.0 | 1.2604230854720464e-16 |
| だ | ラーメン | 0.0 | 0.0 |
| だ | 好き | 0.0 | 0.0 |
| だ | 寿司 | 0.0 | 0.0 |
| だ | 彼 | 0.0 | 0.0 |
| だ | 私 | 0.0 | 0.0 |
| は | ラーメン | 0.0 | 0.0 |
| は | 好き | 0.0 | 0.0 |
| は | 寿司 | 0.0 | 0.0 |
| は | 彼 | 0.0 | 0.0 |
| は | 私 | 0.0 | 0.0 |
| ラーメン | 好き | 0.5 | 0.49999999999999967 |
| ラーメン | 寿司 | 0.9999999999999998 | 1.0 |
| ラーメン | 彼 | 0.7071067811865475 | 0.7071067811865475 |
| ラーメン | 私 | 0.7071067811865475 | 0.7071067811865475 |
| 好き | 寿司 | 0.5 | 0.4999999999999998 |
| 好き | 彼 | 0.0 | -1.73340870411744e-16 |
| 好き | 私 | 0.0 | -1.73340870411744e-16 |
| 寿司 | 彼 | 0.7071067811865475 | 0.7071067811865475 |
| 寿司 | 私 | 0.7071067811865475 | 0.7071067811865475 |
| 彼 | 私 | 1.0 | 1.0000000000000002 |
このように、うまく情報を残しつつ次元を削減することに成功しています。
ただしこのSVDは計算コストが高いため、大規模なコーパスから生成された共起行列を次元圧縮することは現実的ではないという問題もあります。
Bag of Wordsの参考
- シンプルだけど奥が深い、単語で表す文章の特徴
- Bag of Wordsについて書いてみる
- 単語と図で理解する自然言語処理(word2vec, RNN, LSTM)前編
- SVD(特異値分解)解説
- 2017-12-14
Pythonで特異値分解(SVD)を理解する - 次元削減手法(まとめと実装)PCA, LSI(SVD), LDA, ICA, PLIS
Word2Vec
BoWはシンプルながら強力な手法ですが、先に述べた通り大規模コーパスに対しては無力であることや、近年のディープラーニングの台頭によってその座を奪われてきています。特に2013年にGoogleの研究員であったTomas Mikolov氏が発表したWord2Vecという手法が有名です。
この手法とBoWの最大の違いは、単語の分散表現に概念が含まれていることです。
BoWではあくまで単語の前後関係や共起によって分散表現を作成していたため、単語のニュアンスの違いなんかを取り込むことができていません。
例えば「彼女は私の母です」と「必要は発明の母」では、「母」という単語のニュアンスが異なることがお分かりいただけると思います。前者は「親」で、後者は「源」ですね。そういったニュアンスをBoWでは拾うことができません。
これの嬉しいところは以下のような計算が成り立つことです。
v_{王} - v_{男性} + v_{女性} = v_{女王}
上記のように、「王」の概念から「男性」の概念を引き算し、「女性」の概念を足すと「女王」という別の単語を表現することができます。
これは私たち人間がそうであるように、単語の概念までを機械が学習していることを意味しています。
ただし現段階ではまだ言葉から得られる概念情報しか学習していませんので、私たち人間ほどの表現力を得られているかと言われるとそうではありません。それでも非常に大きなブレイクスルーと言えますね。
そんなWord2Vecによる分散表現はCBoWとskip-gramという二つの方法で得ることができます。
CBoW
CBoW: Continuous Bag of Wordsは「ある文章(コンテキスト)の特定の1単語(ターゲット)を隠し、コンテキストからターゲットを推測する」というタスクを解くニューラルネットワークから作成されるWord2Vec分散表現です。
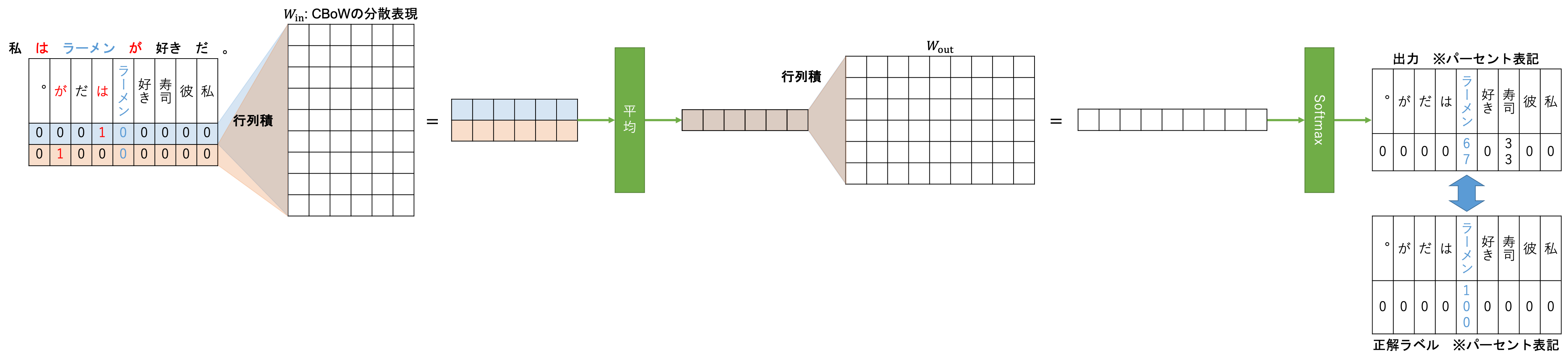
「私はラーメンが好きだ。」をコンテキスト、「ラーメン」をターゲットとしたCBoWのアーキテクチャを説明します。
まず、ターゲット周辺の何単語を参照するか、というウィンドウサイズを決定します。
その後$W_{\textrm{in}}: n_{\textrm{vocab}} \times n_{\textrm{hidden}}$の重みと行列積を取り、それを平均(元論文では合計)します。
その後、$W_{\textrm{out}}: n_{\textrm{hidden}} \times n_{\textrm{vocab}}$の重みと行列積を取り、その出力をSoftmax関数に通して確率に変換します。
そして、正解ラベルとしてターゲットのone-hotベクトルを与え学習します。
そうして学習を進めた結果得られる$W_{\textrm{in}}$がCBoWによって得られる単語の分散表現になります、
アーキテクチャ全体としてはAuto-Encoderと呼ばれるアーキテクチャと似ています。詳しくは参考をご覧になってください。
数式も置いておきます。
\textrm{Forward} \\
\begin{align}
\underbrace{\mathbb{y}_\textrm{hidden}}_{n_\textrm{words} \times n_\textrm{hidden}} &= \underbrace{\mathbb{x}}_{n_\textrm{words} \times n_\textrm{vocab}} \underbrace{\mathbb{W}_\textrm{in}}_{n_\textrm{vocab} \times n_\textrm{hidden}} + \underbrace{\textrm{broadcast}(\underbrace{\mathbb{b}_\textrm{hidden}}_{1 \times n_\textrm{hidden}})}_{n_\textrm{words} \times n_\textrm{hidden}} \\
\underbrace{\mathbb{y}'_\textrm{hidden}}_{1 \times n_\textrm{hidden}} &= \textrm{sum}(\mathbb{y}_\textrm{hidden}, \textrm{axis}=0) \\
\underbrace{\mathbb{y}_\textrm{output}}_{1 \times n_\textrm{vocab}} &= \underbrace{\mathbb{y}'_\textrm{hidden}}_{1 \times n_\textrm{vocab}} \underbrace{\mathbb{W}_\textrm{out}}_{n_\textrm{hidden} \times n_\textrm{vocab}} + \underbrace{\mathbb{b}_\textrm{output}}_{1 \times n_\textrm{vocab}} \\
\underbrace{\mathbb{y}_\textrm{predict}}_{1 \times n_\textrm{vocab}} &= \textrm{Softmax}(\mathbb{y}_\textrm{output})
\end{align}
\textrm{Backward} \\
\begin{align}
\underbrace{\mathbb{\delta}}_{1 \times n_\textrm{vocab}} &= \underbrace{\mathbb{y}_\textrm{predict}}_{1 \times n_\textrm{vocab}} - \underbrace{\mathbb{t}}_{1 \times n_\textrm{vocab}} \\
\underbrace{\mathbb{\delta}_{\mathbb{W}_\textrm{out}}}_{n_\textrm{hidden} \times n_\textrm{vocab}} &= \underbrace{\mathbb{y}'^\top_\textrm{hidden}}_{n_\textrm{hidden} \times 1} \underbrace{\mathbb{\delta}}_{1 \times n_\textrm{vocab}} \\
\underbrace{\mathbb{\delta}_{\mathbb{b}_\textrm{out}}}_{1 \times n_\textrm{vocab}} &= \underbrace{\mathbb{\delta}}_{1 \times n_\textrm{vocab}} \\
\underbrace{\mathbb{\delta}_\textrm{hidden}}_{1 \times n_\textrm{hidden}} &= \underbrace{\mathbb{\delta}}_{1 \times n_\textrm{vocab}} \underbrace{\mathbb{W}^\top_\textrm{out}}_{n_\textrm{vocab} \times n_\textrm{hidden}} \\
\underbrace{\mathbb{\delta}'_\textrm{hidden}}_{n_\textrm{words} \times n_\textrm{hidden}} &= \underbrace{\textrm{broadcast}(\underbrace{\mathbb{\delta}_\textrm{hidden}}_{1 \times n_\textrm{hidden}})}_{n_\textrm{words} \times n_\textrm{hidden}} \\
\underbrace{\mathbb{\delta}_{\mathbb{W}_\textrm{in}}}_{n_\textrm{vocab} \times n_\textrm{hidden}} &= \underbrace{\mathbb{x}^\top}_{n_\textrm{vocab} \times n_\textrm{words}} \underbrace{\mathbb{\delta}'_\textrm{hidden}}_{n_\textrm{words} \times n_\textrm{hidden}} \\
\underbrace{\mathbb{\delta}_{\mathbb{b}_\textrm{hidden}}}_{1 \times n_\textrm{hidden}} &= \underbrace{\textrm{sum}(\underbrace{\mathbb{\delta}'_\textrm{hidden}}_{n_\textrm{words} \times n_\textrm{hidden}}, \textrm{axis}=0)}_{1 \times n_\textrm{hidden}}
\end{align}
実際に計算してみた結果が以下になります。
CBoWのPythonコード
from sklearn.feature_extraction.text import CountVectorizer
corpus = ["私 は ラーメン が 好き だ 。",
"私 は 寿司 が 好き だ 。",
"彼 は ラーメン が 好き だ 。"]
def tokenizer(text):
return text.split(" ")
cv = CountVectorizer(tokenizer=tokenizer)
weights = cv.fit_transform(corpus)
print(cv.get_feature_names())
print(weights.toarray())
import numpy as np
def one_hot(word):
one_hot_vec = np.zeros(len(cv.vocabulary_))
one_hot_vec[cv.vocabulary_[word]] = 1
return one_hot_vec
def get_surround(words, pointer, window_size):
input = words[max(pointer-window_size, 0)
: min(pointer+window_size+1, len(words))]
if pointer-window_size < 0:
del input[pointer]
elif pointer+window_size+1 > len(words):
del input[pointer+window_size+1-len(words)]
else:
del input[window_size]
return input
# CBoW
import matplotlib.pyplot as plt
from tqdm.notebook import trange
np.random.seed(42)
n_vocab = len(cv.vocabulary_)
epoch = 10000
window_size = 1
n_hidden = 6
lr = 1e-2
threshold = 1e-8
interval = 100
words_list = [text.split("\u3000") for text in corpus]
cbow_weight = 1e-2*np.random.randn(n_vocab, n_hidden)
cbow_bias = 1e-2*np.random.randn(1, n_hidden)
out_weight = 1e-2*np.random.randn(n_hidden, n_vocab)
out_bias = 1e-2*np.random.randn(1, n_vocab)
prev_loss = 0.
losses = []
for t in trange(epoch):
loss_per_epoch = 0.
for words in words_list:
indices = list(range(len(words)))
np.random.shuffle(indices)
for i in indices:
# Ready inputs
input = get_surround(words, i, window_size)
ans = words[i]
x = np.array([one_hot(word) for word in input])
y = np.array(one_hot(ans)).reshape(1, -1)
# Forward
hidden = (x@cbow_weight + cbow_bias).mean(axis=0, keepdims=True)
output = hidden@out_weight + out_bias
predict = np.exp(output)/np.sum(np.exp(output), keepdims=True)
# Compute loss
loss = np.sum(-y*np.log(predict+1e-8))
loss_per_epoch += loss
# Backward
delta = predict - y
d_out_weight = hidden.T@delta
d_out_bias = delta.copy()
d_hidden = delta@out_weight.T
d_hidden = np.tile(d_hidden, x.shape[0])\
.reshape(x.shape[0], -1)*x.shape[0]
d_hidden_weight = x.T@d_hidden
d_hidden_bias = np.sum(d_hidden, axis=0, keepdims=True)
# Update
cbow_weight -= lr*d_hidden_weight
cbow_bias -= lr*d_hidden_bias
out_weight -= lr*d_out_weight
out_bias -= lr*d_out_bias
if t%interval == 0:
losses.append(loss_per_epoch)
if abs(prev_loss-loss_per_epoch) < threshold:
break
else:
prev_loss = loss_per_epoch
print(f"epoch {t}: final loss = {loss_per_epoch}")
plt.title("Loss")
plt.xlabel(f"epoch [*{interval}]")
plt.ylabel("error")
plt.yscale("log")
plt.grid()
plt.plot(losses)
- 関数
one_hot:ある単語についてのone-hotベクトル表現を得る関数 - 関数
get_surround:あるターゲット単語(pointerで指示される)の周辺2*window_sizeの単語を取得する関数。ターゲット単語を含まないように取り除く処理のせいで少し複雑に見えると思います。
words_list = [text.split("\u3000") for text in corpus]
cbow_weight = 1e-2*np.random.randn(n_vocab, n_hidden)
cbow_bias = 1e-2*np.random.randn(1, n_hidden)
out_weight = 1e-2*np.random.randn(n_hidden, n_vocab)
out_bias = 1e-2*np.random.randn(1, n_vocab)
ここではコーパスを単語に分割したwords_listと$W_\textrm{in}$と$W_\textrm{out}$を用意しています。$W_\textrm{in}$はcbow_weightという名前の変数として用意しています。また、バイアスも同様に用意しています。
ちなみに"\u300"はUnicodeの半角スペースに対応しています。corpusに含まれる半角スペースがなぜか全て置き換わっていたためこうしています。もしこれでうまくいかない場合は普通に半角スペースでやってみてください。
for words in words_list:
indices = list(range(len(words)))
np.random.shuffle(indices)
# Ready inputs
input = get_surround(words, i, window_size)
ans = words[i]
x = np.array([one_hot(word) for word in input])
y = np.array(one_hot(ans)).reshape(1, -1)
ここではget_surround関数でターゲット単語ansの周辺単語を取得し、xとyにそれぞれのone-hotベクトルを保持しています。
# Forward
hidden = (x@cbow_weight + cbow_bias).mean(axis=0, keepdims=True)
output = hidden@out_weight + out_bias
predict = np.exp(output)/np.sum(np.exp(output), keepdims=True)
# Compute loss
loss = np.sum(-y*np.log(predict+1e-8))
loss_per_epoch += loss
活性化関数にSoftmax関数を用いていることもあるため、ここでは交差エントロピー誤差を用いて誤差を計算しています。$1e-8$を足しているのは$\log$関数の入力がゼロにならないようにするためです。
# Backward
delta = predict - y
d_out_weight = hidden.T@delta
d_out_bias = delta.copy()
d_hidden = delta@out_weight.T
d_hidden = np.tile(d_hidden, x.shape[0])\
.reshape(x.shape[0], -1)*x.shape[0]
d_hidden_weight = x.T@d_hidden
d_hidden_bias = np.sum(d_hidden, axis=0, keepdims=True)
逆伝播の計算については過去記事などをご覧いただければと思います。バッチに対応したコードではないため一部異なる部分もありますが、バッチサイズ1と見做して考えればわかるかと思います。
また、d_hidden = np.tile(d_hidden, x.shape[0]).reshape(x.shape[0], -1)の処理についてですが、順伝播の際に平均を取った部分があったと思いますが、その処理のために行列のサイズが変更されてしまったためコピーするような形で形状を復元しています。さらに平均を計算する際にはx.shape[0]つまりデータの個数で割り算しているためx.shape[0]を掛けることで辻褄を合わせています。
# Update
cbow_weight -= lr*d_hidden_weight
cbow_bias -= lr*d_hidden_bias
out_weight -= lr*d_out_weight
out_bias -= lr*d_out_bias
パラメータの更新はSGDで行っています。
ウィンドウサイズは、論文では10を用いているようですが、今回は小さすぎるコーパスに対する学習なのでwindow_size = 1で計算しています。
print(cbow_weight)
[[ 0.33182162 3.29596091 1.80855084 1.71448059 0.9885287 -2.93372024]
[ 4.42062037 0.58321929 3.12210101 0.49071031 -0.82889288 -4.7565911 ]
[ 3.32298824 -3.11871086 -2.03274293 -0.06673988 0.10913592 -4.49169164]
[-1.35534626 0.54776265 2.10413095 -0.57199091 0.1944737 1.90349456]
[-1.96240284 -1.21610264 -1.89181389 -0.67280184 -0.62877591 3.64013407]
[-1.85480889 4.8385026 -2.0222571 0.02124056 3.03893178 0.33977704]
[-1.55839835 -0.98132815 -1.80242746 -0.7266289 -0.3734114 3.06063833]
[-0.43488751 -1.61185204 0.1345924 0.13392771 -1.3739515 1.340451 ]
[-0.90463249 -2.11036897 0.00860975 0.11729932 -1.68082579 2.09484829]]
学習した結果を見てみましょう。
from pprint import pprint
vocab = sorted(cv.vocabulary_, key=lambda x: x[0])
for words in words_list:
indices = list(range(len(words)))
for i in indices:
# Ready inputs
input = get_surround(words, i, window_size)
ans = words[i]
x = np.array([one_hot(word) for word in input])
y = np.array(one_hot(ans)).reshape(1, -1)
print(f"入力: {input}\t正解: {ans}")
# Forward
hidden = (x@cbow_weight + cbow_bias).mean(axis=0, keepdims=True)
output = hidden@out_weight + out_bias
predict = np.exp(output)/np.sum(np.exp(output), keepdims=True)
pprint(dict(zip(vocab, predict[0])))
print("-----")
推論結果
入力: ['は'] 正解: 私
{'。': 1.0609735644032356e-10,
'が': 0.0005148065620589125,
'だ': 2.1652549537413823e-05,
'は': 0.0007521753056085488,
'ラーメン': 3.314204030492522e-05,
'好き': 1.2783030853537752e-09,
'寿司': 2.1799386307850823e-05,
'彼': 0.34903517227537956,
'私': 0.6496212504964022}
-----
入力: ['私', 'ラーメン'] 正解: は
{'。': 5.822687037111103e-05,
'が': 9.343894336440986e-05,
'だ': 4.751967933819793e-11,
'は': 0.9998316175288404,
'ラーメン': 9.296578097367661e-11,
'好き': 6.931537725801257e-11,
'寿司': 8.518601274566906e-11,
'彼': 8.025138435562832e-06,
'私': 8.691224001699407e-06}
-----
入力: ['は', 'が'] 正解: ラーメン
{'。': 6.695462930240341e-09,
'が': 2.517612237837813e-08,
'だ': 0.0003030921861392993,
'は': 6.603990952301419e-07,
'ラーメン': 0.665660793437573,
'好き': 0.0010368999907446406,
'寿司': 0.33231286513481473,
'彼': 0.0002646629535473338,
'私': 0.0004209940265004653}
-----
入力: ['ラーメン', '好き'] 正解: が
{'。': 6.666590824923218e-07,
'が': 0.9997484882015913,
'だ': 8.677312162209899e-05,
'は': 0.00012453918538858817,
'ラーメン': 1.7253303891964961e-10,
'好き': 1.0228938051243059e-10,
'寿司': 1.6177153059318543e-10,
'彼': 1.6972152424687814e-05,
'私': 2.2560243296882435e-05}
-----
入力: ['が', 'だ'] 正解: 好き
{'。': 0.0007981490846108894,
'が': 5.771128414025364e-15,
'だ': 4.622410091849169e-09,
'は': 2.4469538972070834e-11,
'ラーメン': 0.0002961118604773813,
'好き': 0.9987447674593978,
'寿司': 0.00016096694858177426,
'彼': 2.404278737146331e-14,
'私': 2.2805764162340577e-14}
-----
入力: ['好き', '。'] 正解: だ
{'。': 4.523072097641837e-12,
'が': 0.00020279548379928985,
'だ': 0.9997925761310679,
'は': 1.4116428170736628e-11,
'ラーメン': 1.544836591094253e-06,
'好き': 1.9502427789887074e-08,
'寿司': 9.952116906697878e-07,
'彼': 7.57800405177982e-07,
'私': 1.3110153785717838e-06}
-----
入力: ['だ'] 正解: 。
{'。': 0.9992140113641594,
'が': 1.792813031379192e-17,
'だ': 3.337671866742168e-15,
'は': 6.843918640824542e-13,
'ラーメン': 4.346423325570966e-12,
'好き': 0.0007859886274165869,
'寿司': 3.3897721929460857e-12,
'彼': 1.9089723897061755e-21,
'私': 1.2634112679770324e-21}
-----
入力: ['は'] 正解: 私
{'。': 1.0609735644032356e-10,
'が': 0.0005148065620589125,
'だ': 2.1652549537413823e-05,
'は': 0.0007521753056085488,
'ラーメン': 3.314204030492522e-05,
'好き': 1.2783030853537752e-09,
'寿司': 2.1799386307850823e-05,
'彼': 0.34903517227537956,
'私': 0.6496212504964022}
-----
入力: ['私', '寿司'] 正解: は
{'。': 0.0001825088749576217,
'が': 0.00017818910334115634,
'だ': 2.887585203154446e-10,
'は': 0.9996099456123885,
'ラーメン': 5.729797501855008e-10,
'好き': 5.643549517865313e-10,
'寿司': 5.151183506617318e-10,
'彼': 1.405576538396299e-05,
'私': 1.5298702717070157e-05}
-----
入力: ['は', 'が'] 正解: 寿司
{'。': 6.695462930240341e-09,
'が': 2.517612237837813e-08,
'だ': 0.0003030921861392993,
'は': 6.603990952301419e-07,
'ラーメン': 0.665660793437573,
'好き': 0.0010368999907446406,
'寿司': 0.33231286513481473,
'彼': 0.0002646629535473338,
'私': 0.0004209940265004653}
-----
入力: ['寿司', '好き'] 正解: が
{'。': 1.0956090794981646e-06,
'が': 0.9996207490623651,
'だ': 0.0002764635051340212,
'は': 6.528313551888231e-05,
'ラーメン': 5.575447181204144e-10,
'好き': 4.366611753980282e-10,
'寿司': 5.128993013401411e-10,
'彼': 1.55858385199604e-05,
'私': 2.082134227742978e-05}
-----
入力: ['が', 'だ'] 正解: 好き
{'。': 0.0007981490846108894,
'が': 5.771128414025364e-15,
'だ': 4.622410091849169e-09,
'は': 2.4469538972070834e-11,
'ラーメン': 0.0002961118604773813,
'好き': 0.9987447674593978,
'寿司': 0.00016096694858177426,
'彼': 2.404278737146331e-14,
'私': 2.2805764162340577e-14}
-----
入力: ['好き', '。'] 正解: だ
{'。': 4.523072097641837e-12,
'が': 0.00020279548379928985,
'だ': 0.9997925761310679,
'は': 1.4116428170736628e-11,
'ラーメン': 1.544836591094253e-06,
'好き': 1.9502427789887074e-08,
'寿司': 9.952116906697878e-07,
'彼': 7.57800405177982e-07,
'私': 1.3110153785717838e-06}
-----
入力: ['だ'] 正解: 。
{'。': 0.9992140113641594,
'が': 1.792813031379192e-17,
'だ': 3.337671866742168e-15,
'は': 6.843918640824542e-13,
'ラーメン': 4.346423325570966e-12,
'好き': 0.0007859886274165869,
'寿司': 3.3897721929460857e-12,
'彼': 1.9089723897061755e-21,
'私': 1.2634112679770324e-21}
-----
入力: ['は'] 正解: 彼
{'。': 1.0609735644032356e-10,
'が': 0.0005148065620589125,
'だ': 2.1652549537413823e-05,
'は': 0.0007521753056085488,
'ラーメン': 3.314204030492522e-05,
'好き': 1.2783030853537752e-09,
'寿司': 2.1799386307850823e-05,
'彼': 0.34903517227537956,
'私': 0.6496212504964022}
-----
入力: ['彼', 'ラーメン'] 正解: は
{'。': 0.00019788001168226393,
'が': 0.0002780338887341041,
'だ': 7.559156783428679e-10,
'は': 0.9994778212071774,
'ラーメン': 1.231315247784555e-09,
'好き': 1.0471452688529702e-09,
'寿司': 1.0952014156579716e-09,
'彼': 2.206344409587853e-05,
'私': 2.4197318732700544e-05}
-----
入力: ['は', 'が'] 正解: ラーメン
{'。': 6.695462930240341e-09,
'が': 2.517612237837813e-08,
'だ': 0.0003030921861392993,
'は': 6.603990952301419e-07,
'ラーメン': 0.665660793437573,
'好き': 0.0010368999907446406,
'寿司': 0.33231286513481473,
'彼': 0.0002646629535473338,
'私': 0.0004209940265004653}
-----
入力: ['ラーメン', '好き'] 正解: が
{'。': 6.666590824923218e-07,
'が': 0.9997484882015913,
'だ': 8.677312162209899e-05,
'は': 0.00012453918538858817,
'ラーメン': 1.7253303891964961e-10,
'好き': 1.0228938051243059e-10,
'寿司': 1.6177153059318543e-10,
'彼': 1.6972152424687814e-05,
'私': 2.2560243296882435e-05}
-----
入力: ['が', 'だ'] 正解: 好き
{'。': 0.0007981490846108894,
'が': 5.771128414025364e-15,
'だ': 4.622410091849169e-09,
'は': 2.4469538972070834e-11,
'ラーメン': 0.0002961118604773813,
'好き': 0.9987447674593978,
'寿司': 0.00016096694858177426,
'彼': 2.404278737146331e-14,
'私': 2.2805764162340577e-14}
-----
入力: ['好き', '。'] 正解: だ
{'。': 4.523072097641837e-12,
'が': 0.00020279548379928985,
'だ': 0.9997925761310679,
'は': 1.4116428170736628e-11,
'ラーメン': 1.544836591094253e-06,
'好き': 1.9502427789887074e-08,
'寿司': 9.952116906697878e-07,
'彼': 7.57800405177982e-07,
'私': 1.3110153785717838e-06}
-----
入力: ['だ'] 正解: 。
{'。': 0.9992140113641594,
'が': 1.792813031379192e-17,
'だ': 3.337671866742168e-15,
'は': 6.843918640824542e-13,
'ラーメン': 4.346423325570966e-12,
'好き': 0.0007859886274165869,
'寿司': 3.3897721929460857e-12,
'彼': 1.9089723897061755e-21,
'私': 1.2634112679770324e-21}
-----
単語同士の類似度は次のようになります。
sim1 = cosine_similarity(u[:, :6]@np.diag(s[:6]))
sim2 = cosine_similarity(cbow_weight)
for i in range(n_vocab):
for j in range(i+1, n_vocab):
print(f"|{id2w[i]}|{id2w[j]}|{sim1[i, j]}|{sim2[i, j]}|")
| 単語1 | 単語2 | 圧縮後の類似度 | CBoWの類似度 |
|---|---|---|---|
| 。 | が | 0.0 | 0.609909267404925 |
| 。 | だ | 0.0 | 0.009153085757579602 |
| 。 | は | 0.0 | -0.0720924140530391 |
| 。 | ラーメン | -9.358134352140677e-16 | -0.8274765324776887 |
| 。 | 好き | 0.7071067811865472 | 0.41772277379276707 |
| 。 | 寿司 | -8.309365609351454e-16 | -0.8332996025489453 |
| 。 | 彼 | -3.320011377892241e-16 | -0.7784692094789452 |
| 。 | 私 | -3.320011377892241e-16 | -0.8116561341637417 |
| が | だ | 0.5669467095138412 | 0.5669983227509734 |
| が | は | 0.4225771273642582 | -0.3629679436604853 |
| が | ラーメン | 0.0 | -0.92665413413469 |
| が | 好き | 0.0 | -0.3416646040237181 |
| が | 寿司 | 0.0 | -0.9299612266464419 |
| が | 彼 | 0.0 | -0.409256386940455 |
| が | 私 | 0.0 | -0.5320033309714258 |
| だ | は | 1.2604230854720464e-16 | -0.8700796580043243 |
| だ | ラーメン | 0.0 | -0.4736742686622143 |
| だ | 好き | 0.0 | -0.4302351410010142 |
| だ | 寿司 | 0.0 | -0.4446869259943875 |
| だ | 彼 | 0.0 | -0.1676312696537884 |
| だ | 私 | 0.0 | -0.25452483221675776 |
| は | ラーメン | 0.0 | 0.3340135182598704 |
| は | 好き | 0.0 | 0.10352885536139433 |
| は | 寿司 | 0.0 | 0.2978448177749703 |
| は | 彼 | 0.0 | 0.26516784588968123 |
| は | 私 | 0.0 | 0.3205773407239325 |
| ラーメン | 好き | 0.49999999999999967 | 0.02933748077676704 |
| ラーメン | 寿司 | 1.0 | 0.9968913675149247 |
| ラーメン | 彼 | 0.7071067811865475 | 0.6711319610805653 |
| ラーメン | 私 | 0.7071067811865475 | 0.7623964769346193 |
| 好き | 寿司 | 0.4999999999999998 | 0.06470027335208178 |
| 好き | 彼 | -1.73340870411744e-16 | -0.6781678528890698 |
| 好き | 私 | -1.73340870411744e-16 | -0.576792783437659 |
| 寿司 | 彼 | 0.7071067811865475 | 0.6273489513852494 |
| 寿司 | 私 | 0.7071067811865475 | 0.7216938353221249 |
| 彼 | 私 | 1.0000000000000002 | 0.9900462932199341 |
これを見てみると、「彼」と「私」や「ラーメン」と「寿司」といった、BoWの分散表現でも類似度が高かった単語のペアについては同様に高い類似度となっていることがわかります。また、「好き」と「彼」などの意味の異なった単語のペアについては負の類似度となっており、より遠い分散表現が得られていることもわかります。
これまでと決定的に異なるのが、類似度が負になっているものが存在することです。
(「。」と「ラーメン」の圧縮後類似度$-9.358134352140677e-16$などは数値誤差です)
これはBoWで作成された共起行列が全ての要素が正であったのに対して、CBoWによって生成された分散表現は最初から負の値を取り得ることに由来します。だからどうということはありませんが、強いて言えばこれまで$0 \le \cos \theta \le 1 \Leftrightarrow 0° \le \theta \le 90°$だった表現範囲が$-1 \le \cos \theta \le 1 \Leftrightarrow 0° \le \theta \le 180°$に広がることで、使われる文脈や意味が全く異なる単語同士をより遠ざける形で表現することができるようになります。~~とはいえBoWの共起行列を例えば標準化するなどして負の値を取り得るようにスケーリングすれば大差ないと思われます。~~標準化ではデータ同士の位置関係が変わらないので類似度は変わらないですね…
skip-gram
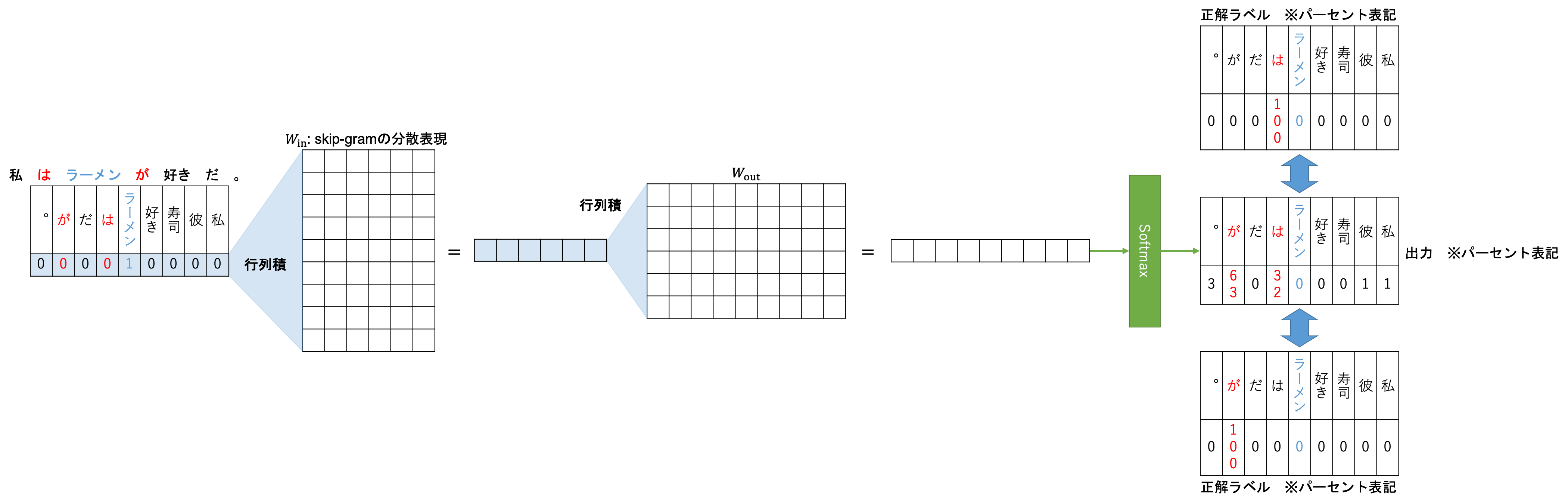
続いてskip-gramの説明です。skip-gramはCBoWとは逆に「ある文章(コンテキスト)の特定の1単語(ターゲット)に注目し、ターゲットからコンテキスト内の周辺語を推測する」というタスクを解くニューラルネットワークから作成されるWord2Vec分散表現です。
基本のアーキテクチャはCBoWと同じです。異なる点としては、ターゲット周辺の何単語を推測するかというウィンドウサイズについて、skip-gramではこのウィンドウサイズ$C$はあくまで最大単語数であり、学習時には単語ごとに$1 \le R \le C$である$R$をランダムに決定、ウィンドウサイズとするようです。
結局周辺$2R$語を推測するように学習を進めるので、逆伝播時は複数の正解ラベルそれぞれについて逆伝播が行われ学習されます。
skip-gramのPythonコード
from sklearn.feature_extraction.text import CountVectorizer
corpus = ["私 は ラーメン が 好き だ 。",
"私 は 寿司 が 好き だ 。",
"彼 は ラーメン が 好き だ 。"]
def tokenizer(text):
return text.split(" ")
cv = CountVectorizer(tokenizer=tokenizer)
weights = cv.fit_transform(corpus)
print(cv.get_feature_names())
print(weights.toarray())
import numpy as np
def one_hot(word):
one_hot_vec = np.zeros(len(cv.vocabulary_))
one_hot_vec[cv.vocabulary_[word]] = 1
return one_hot_vec
def get_surround(words, pointer, window_size):
input = words[max(pointer-window_size, 0)
: min(pointer+window_size+1, len(words))]
if pointer-window_size < 0:
del input[pointer]
elif pointer+window_size+1 > len(words):
del input[pointer+window_size+1-len(words)]
else:
del input[window_size]
return input
# Skip-gram
import matplotlib.pyplot as plt
from tqdm.notebook import trange
np.random.seed(42)
n_vocab = len(cv.vocabulary_)
epoch = 10000
window_size = 1
n_hidden = 6
lr = 1e-2
threshold = 1e-8
interval = 100
words_list = [text.split("\u3000") for text in corpus]
sg_weight = 1e-2*np.random.randn(n_vocab, n_hidden)
sg_bias = 1e-2*np.random.randn(1, n_hidden)
out_weight = 1e-2*np.random.randn(n_hidden, n_vocab)
out_bias = 1e-2*np.random.randn(1, n_vocab)
prev_loss = 0.
losses = []
for t in trange(epoch):
loss_per_epoch = 0.
for words in words_list:
indices = list(range(len(words)))
np.random.shuffle(indices)
for i in indices:
# Ready inputs
R = np.random.randint(1, window_size, 1)[0] \
if window_size > 1 else 1
input = words[i]
ans = get_surround(words, i, R)
x = np.array(one_hot(input)).reshape(1, -1)
y = np.array([one_hot(a) for a in ans])
for j in range(len(y)):
# Forward
hidden = (x@sg_weight + sg_bias).mean(axis=0, keepdims=True)
output = hidden@out_weight + out_bias
predict = np.exp(output)/np.sum(np.exp(output), keepdims=True)
# Compute loss
loss = np.sum(-y[j]*np.log(predict+1e-8))
loss_per_epoch += loss/len(y)
# Backward
delta = predict - y[j]
d_out_weight = hidden.T@delta
d_out_bias = delta.copy()
d_hidden = delta@out_weight.T
d_hidden = np.tile(d_hidden, x.shape[0])\
.reshape(x.shape[0], -1)*x.shape[0]
d_hidden_weight = x.T@d_hidden
d_hidden_bias = np.sum(d_hidden, axis=0, keepdims=True)
# Update
sg_weight -= lr*d_hidden_weight
sg_bias -= lr*d_hidden_bias
out_weight -= lr*d_out_weight
out_bias -= lr*d_out_bias
if t%interval == 0:
losses.append(loss_per_epoch)
if abs(prev_loss-loss_per_epoch) < threshold:
break
else:
prev_loss = loss_per_epoch
print(f"epoch {t}: final loss = {loss_per_epoch}")
plt.title("Loss")
plt.xlabel(f"epoch [*{interval}]")
plt.ylabel("error")
plt.yscale("log")
plt.grid()
plt.plot(losses)
# Ready inputs
R = np.random.randint(1, window_size, 1)[0] \
if window_size > 1 else 1
input = words[i]
ans = get_surround(words, i, R)
x = np.array(one_hot(input)).reshape(1, -1)
y = np.array([one_hot(a) for a in ans])
ここでは、論文に基づいて$R$(コードでもR)を区間$[ 1, C ]$からランダムに選択しています。また、CBoWとは逆に入力が1単語、正解ラベルが複数単語になっています。そのため、正解ラベルの数だけ予測と学習を繰り返しています。
# Compute loss
loss = np.sum(-y[j]*np.log(predict+1e-8))
loss_per_epoch += loss/len(y)
また、誤差の和を取る部分については周辺語の平均となるようにlen(y)で割っています。ここは以降の逆伝播などには何の影響もありませんので注意してください。
こちらもCBoWと同じくwindow_size = 1で計算しています。
print(sg_weight)
[[ 0.22918108 3.27339991 1.01933343 1.62012079 0.90708405 -1.87913403]
[ 1.92863191 -0.18998641 0.63026778 0.31104666 -0.96804493 -1.30171052]
[ 0.91455334 -1.60046135 -1.44311189 -0.11350698 0.1882469 -1.22089379]
[ 0.03130425 0.15936981 2.28005579 -0.24015382 -0.30449253 -0.30488771]
[-0.65139756 0.07268524 -0.8830847 -0.64017036 0.29955563 0.90378271]
[-0.01706015 1.73207229 -0.53333987 -0.02213297 0.87569538 -0.73323909]
[-0.69017767 0.08911927 -0.91040053 -0.5718911 0.31271512 0.94028928]
[-0.9331444 -1.7166072 -0.1407946 -0.09515354 -0.66507651 1.86743211]
[-1.04681312 -1.89507196 -0.14929907 -0.12282586 -0.71885323 2.06789077]]
学習した結果を見てみましょう。
from pprint import pprint
vocab = sorted(cv.vocabulary_, key=lambda x: x[0])
for w in vocab:
print(f"入力: {w}")
x = np.array(one_hot(w)).reshape(1, -1)
hidden = (x@sg_weight + sg_bias).mean(axis=0, keepdims=True)
output = hidden@out_weight + out_bias
predict = np.exp(output)/np.sum(np.exp(output), keepdims=True)
pprint(dict(zip(vocab, predict[0])))
print("-----")
推論結果
入力: 。
{'。': 1.3239144469353089e-11,
'が': 4.997960641851731e-06,
'だ': 0.9953541139461264,
'は': 2.7764377943304236e-10,
'ラーメン': 0.0029334363806121826,
'好き': 4.156457738226211e-06,
'寿司': 0.0016107709974398344,
'彼': 3.296126979500019e-05,
'私': 5.9562696763635615e-05}
-----
入力: が
{'。': 0.003750567158263297,
'が': 4.6082159270331885e-06,
'だ': 0.00040077422095905195,
'は': 0.0022721541309448307,
'ラーメン': 0.46913935984891403,
'好き': 0.24522084134677866,
'寿司': 0.2787180947026821,
'彼': 0.0002211656663196101,
'私': 0.00027243470921139003}
-----
入力: だ
{'。': 0.999683681192532,
'が': 2.0781415981557574e-07,
'だ': 1.575452959656423e-08,
'は': 3.323019550369056e-05,
'ラーメン': 5.0407529230776816e-08,
'好き': 0.0002827713094001281,
'寿司': 4.236466694912832e-08,
'彼': 4.83308265628484e-10,
'私': 4.783703110315912e-10}
-----
入力: は
{'。': 1.9926673722233226e-07,
'が': 3.944848935196329e-05,
'だ': 0.001273750362798691,
'は': 0.0008035261033390624,
'ラーメン': 0.19043722995177081,
'好き': 0.00013786538197888663,
'寿司': 0.11138844469334282,
'彼': 0.25197135513294683,
'私': 0.4439481806177338}
-----
入力: ラーメン
{'。': 0.030621933625714613,
'が': 0.6272492949309988,
'だ': 0.0007105296052037572,
'は': 0.3232780232004582,
'ラーメン': 2.0850260411694235e-05,
'好き': 3.628245440637999e-05,
'寿司': 1.7564913242835294e-05,
'彼': 0.007804837976783651,
'私': 0.010260683032780079}
-----
入力: 好き
{'。': 0.00034132550315504136,
'が': 0.13567178050756493,
'だ': 0.8540807940472728,
'は': 0.00015254636533529342,
'ラーメン': 0.002195227027657093,
'好き': 0.0012317746614613349,
'寿司': 0.0015773831322773084,
'彼': 0.0019359594395280007,
'私': 0.0028132093157481604}
-----
入力: 寿司
{'。': 0.02596015296223942,
'が': 0.6471093892239984,
'だ': 0.0006869182528065833,
'は': 0.30928869850403423,
'ラーメン': 1.6296588507389384e-05,
'好き': 2.7582244911429927e-05,
'寿司': 1.3776447797611234e-05,
'彼': 0.0073017608716218286,
'私': 0.00959542490408305}
-----
入力: 彼
{'。': 0.0006886901127857259,
'が': 0.0002394993503714032,
'だ': 1.0601767462960285e-08,
'は': 0.9979556747590752,
'ラーメン': 1.0357454864861101e-07,
'好き': 4.780942057025719e-08,
'寿司': 8.769333122796121e-08,
'彼': 0.0004940507565143427,
'私': 0.0006218353421854127}
-----
入力: 私
{'。': 0.0003960805040578411,
'が': 0.0001245294100118911,
'だ': 2.201065392078026e-09,
'は': 0.9988409627917361,
'ラーメン': 2.6262479602017902e-08,
'好き': 1.194485661361012e-08,
'寿司': 2.2613010871820793e-08,
'彼': 0.00028344042859080237,
'私': 0.00035492384419081745}
-----
単語同士の類似度は次のようになります。
sim1 = cosine_similarity(u[:, :6]@np.diag(s[:6]))
sim2 = cosine_similarity(sg_weight)
for i in range(n_vocab):
for j in range(i+1, n_vocab):
print(f"|{id2w[i]}|{id2w[j]}|{sim1[i, j]}|{sim2[i, j]}|")
| 単語1 | 単語2 | 圧縮後の類似度 | skip-gramの類似度 |
|---|---|---|---|
| 。 | が | 0.0 | 0.2229174802585368 |
| 。 | だ | 0.0 | -0.3674335855441274 |
| 。 | は | 0.0 | 0.2723764188044039 |
| 。 | ラーメン | -9.358134352140677e-16 | -0.4754847189450626 |
| 。 | 好き | 0.7071067811865472 | 0.7817025671798838 |
| 。 | 寿司 | -8.309365609351454e-16 | -0.456552927920765 |
| 。 | 彼 | -3.8116456325797087e-16 | -0.8475062385217488 |
| 。 | 私 | -3.8116456325797087e-16 | -0.8475173155982927 |
| が | だ | 0.5669467095138412 | 0.3640402874596618 |
| が | は | 0.42257712736425806 | 0.33974348880014726 |
| が | ラーメン | 0.0 | -0.8376685971974773 |
| が | 好き | 0.0 | -0.1064519129339985 |
| が | 寿司 | 0.0 | -0.8537253881767827 |
| が | 彼 | 0.0 | -0.46191969042634284 |
| が | 私 | 0.0 | -0.467964176110694 |
| だ | は | 5.891059824436164e-17 | -0.5124080998028411 |
| だ | ラーメン | 0.0 | -0.0978580102078866 |
| だ | 好き | 0.0 | -0.16833614115052817 |
| だ | 寿司 | 0.0 | -0.11287169955655381 |
| だ | 彼 | 0.0 | -0.0402272194888962 |
| だ | 私 | 0.0 | -0.04343022317483239 |
| は | ラーメン | 0.0 | -0.6014626995143739 |
| は | 好き | 0.0 | -0.19527698014885694 |
| は | 寿司 | 0.0 | -0.614719779635031 |
| は | 彼 | 0.0 | -0.14841524375627319 |
| は | 私 | 0.0 | -0.14655646280689358 |
| ラーメン | 好き | 0.4999999999999997 | 0.06514039650248336 |
| ラーメン | 寿司 | 1.0 | 0.9984870144582699 |
| ラーメン | 彼 | 0.7071067811865474 | 0.4866769208968102 |
| ラーメン | 私 | 0.7071067811865474 | 0.4911721963613695 |
| 好き | 寿司 | 0.49999999999999983 | 0.07169858308098982 |
| 好き | 彼 | -1.6799257269068767e-16 | -0.808795571847555 |
| 好き | 私 | -1.6799257269068767e-16 | -0.806128868561986 |
| 寿司 | 彼 | 0.7071067811865474 | 0.49199579367023183 |
| 寿司 | 私 | 0.7071067811865474 | 0.4963165645318926 |
| 彼 | 私 | 1.0 | 0.999954515885256 |
CBoWと同じくいい感じに単語同士の類似度が取れています。比較もしておきましょう。
sim1 = cosine_similarity(u[:, :6]@np.diag(s[:6]))
sim2 = cosine_similarity(cbow_weight)
sim3 = cosine_similarity(sg_weight)
for i in range(n_vocab):
for j in range(i+1, n_vocab):
print(f"|{id2w[i]}|{id2w[j]}|{sim1[i, j]}|{sim2[i, j]}|{sim3[i, j]}|")
| 単語1 | 単語2 | 圧縮後の類似度 | CBoWの類似度 | skip-gramの類似度 |
|---|---|---|---|---|
| 。 | が | 0.0 | 0.609909267404925 | 0.2229174802585368 |
| 。 | だ | 0.0 | 0.009153085757579602 | -0.3674335855441274 |
| 。 | は | 0.0 | -0.0720924140530391 | 0.2723764188044039 |
| 。 | ラーメン | -9.358134352140677e-16 | -0.8274765324776887 | -0.4754847189450626 |
| 。 | 好き | 0.7071067811865472 | 0.41772277379276707 | 0.7817025671798838 |
| 。 | 寿司 | -8.309365609351454e-16 | -0.8332996025489453 | -0.456552927920765 |
| 。 | 彼 | -3.8116456325797087e-16 | -0.7784692094789452 | -0.8475062385217488 |
| 。 | 私 | -3.8116456325797087e-16 | -0.8116561341637417 | -0.8475173155982927 |
| が | だ | 0.5669467095138412 | 0.5669983227509734 | 0.3640402874596618 |
| が | は | 0.42257712736425806 | -0.3629679436604853 | 0.33974348880014726 |
| が | ラーメン | 0.0 | -0.92665413413469 | -0.8376685971974773 |
| が | 好き | 0.0 | -0.3416646040237181 | -0.1064519129339985 |
| が | 寿司 | 0.0 | -0.9299612266464419 | -0.8537253881767827 |
| が | 彼 | 0.0 | -0.409256386940455 | -0.46191969042634284 |
| が | 私 | 0.0 | -0.5320033309714258 | -0.467964176110694 |
| だ | は | 5.891059824436164e-17 | -0.8700796580043243 | -0.5124080998028411 |
| だ | ラーメン | 0.0 | -0.4736742686622143 | -0.0978580102078866 |
| だ | 好き | 0.0 | -0.4302351410010142 | -0.16833614115052817 |
| だ | 寿司 | 0.0 | -0.4446869259943875 | -0.11287169955655381 |
| だ | 彼 | 0.0 | -0.1676312696537884 | -0.0402272194888962 |
| だ | 私 | 0.0 | -0.25452483221675776 | -0.04343022317483239 |
| は | ラーメン | 0.0 | 0.3340135182598704 | -0.6014626995143739 |
| は | 好き | 0.0 | 0.10352885536139433 | -0.19527698014885694 |
| は | 寿司 | 0.0 | 0.2978448177749703 | -0.614719779635031 |
| は | 彼 | 0.0 | 0.26516784588968123 | -0.14841524375627319 |
| は | 私 | 0.0 | 0.3205773407239325 | -0.14655646280689358 |
| ラーメン | 好き | 0.4999999999999997 | 0.02933748077676704 | 0.06514039650248336 |
| ラーメン | 寿司 | 1.0 | 0.9968913675149247 | 0.9984870144582699 |
| ラーメン | 彼 | 0.7071067811865474 | 0.6711319610805653 | 0.4866769208968102 |
| ラーメン | 私 | 0.7071067811865474 | 0.7623964769346193 | 0.4911721963613695 |
| 好き | 寿司 | 0.49999999999999983 | 0.06470027335208178 | 0.07169858308098982 |
| 好き | 彼 | -1.6799257269068767e-16 | -0.6781678528890698 | -0.808795571847555 |
| 好き | 私 | -1.6799257269068767e-16 | -0.576792783437659 | -0.806128868561986 |
| 寿司 | 彼 | 0.7071067811865474 | 0.6273489513852494 | 0.49199579367023183 |
| 寿司 | 私 | 0.7071067811865474 | 0.7216938353221249 | 0.4963165645318926 |
| 彼 | 私 | 1.0 | 0.9900462932199341 | 0.999954515885256 |
こうしてみると傾向は同じような感じになっていますが、よくよくみるとかなり異なっていることがわかります。
「私」と「彼」や「ラーメン」と「寿司」などの、同様の文脈で登場する単語同士の類似度はともに高いですが、名詞同士である「私」と「ラーメン」などについては、CBoWではかなり類似度が高く見積もられていますが、skip-gramでは少し抑えられています。さらに、品詞が異なる「は」と「私」などの類似度はskip-gramでは負の値を取るほど離れていることがわかります。
これにも見られる通り、CBoWよりもskip-gramで生成された分散表現の方が単語の概念的により的確なものである場合が多いようです。ただし学習コストはskip-gramの方が高くなります。
分散表現の図示
ここまで色々と単語の分散表現を見てきましたが、数字ばっかりコードばっかりで直感的ではありません。今回はただ数個の単語を分析するだけでしたのでまだ大丈夫ですが、もし数万単語もあれば飽き飽きするというか、嫌になりますよね。ということでより直感的に見られるように図示してみます。
!pip install japanize-matplotlib
import japanize_matplotlib
from sklearn.decomposition import PCA
# CBoW
pca = PCA(n_components=2)
pca.fit(cbow_weight)
data_pca = pca.transform(cbow_weight)
for i in range(n_vocab):
plt.plot(data_pca[i][0], data_pca[i][1], ms=5.0, zorder=2, marker="x")
plt.annotate(id2w[i], (data_pca[i][0], data_pca[i][1]))
plt.title("CBoW")
plt.show()
# skip-gram
pca = PCA(n_components=2)
pca.fit(sg_weight)
data_pca = pca.transform(sg_weight)
for i in range(n_vocab):
plt.plot(data_pca[i][0], data_pca[i][1], ms=5.0, zorder=2, marker="x")
plt.annotate(id2w[i], (data_pca[i][0], data_pca[i][1]))
plt.title("skip-gram")
plt.show()
図示する際はPCAによって分散表現を2次元に落とし込んでいます。こうして見比べるとそれぞれの位置関係は割と似ていますが、skip-gramでは似ているものはより近くに、似ていないものはより遠くにありますね。
今回の超小規模なデータセットでも比較的綺麗に分かれていますし、もっと大規模なコーパスに対してしっかり学習した結果も図示してみたいものです。
Word2Vecの参考
- https://www.anarchive-beta.com/entry/2020/10/23/190000
- Word2Vecを理解する
- Word2vecとは|モデルの種類やその仕組み、活用事例まで紹介!
- Word2Vec:発明した本人も驚く単語ベクトルの驚異的な力
- 単語と図で理解する自然言語処理(word2vec, RNN, LSTM)前編
- word2vec(Skip-Gram Model)の仕組みを恐らく日本一簡潔にまとめてみたつもり
- 元論文: Efficient Estimation of Word Representations in
Vector Space - Is word2vec basically an autoencoder?
- 【pythonで自然言語処理】word2vecで分散表現した単語を2次元に可視化する
- グラフに日本語フォントで出力するには
おわりに
自然言語処理を腰を据えて勉強始めました。難しいですね〜