時系列逐次スプライン補間の実践（前編）

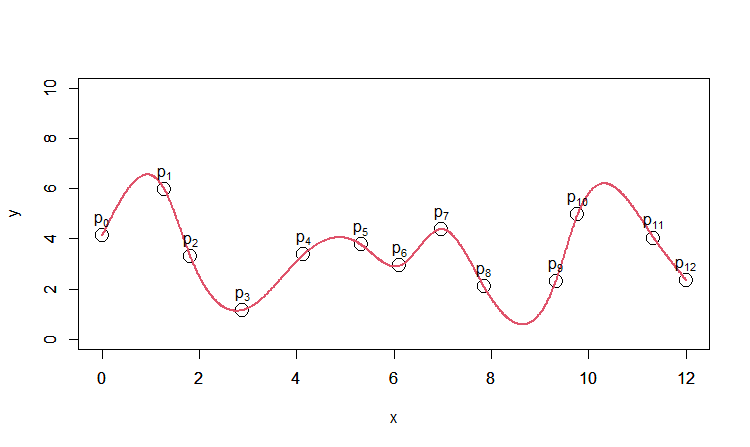
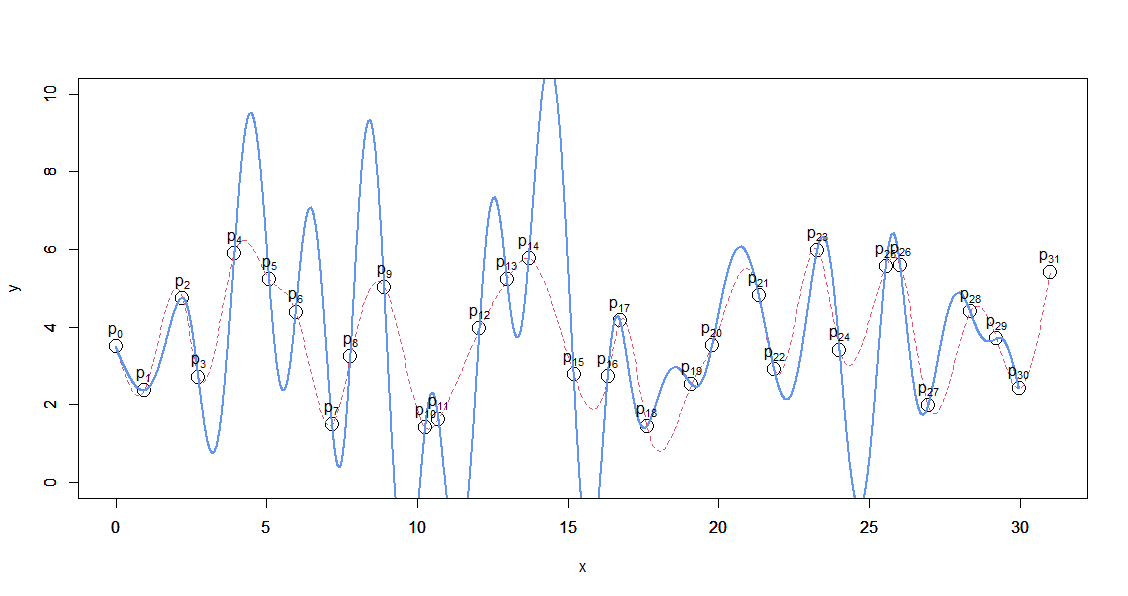
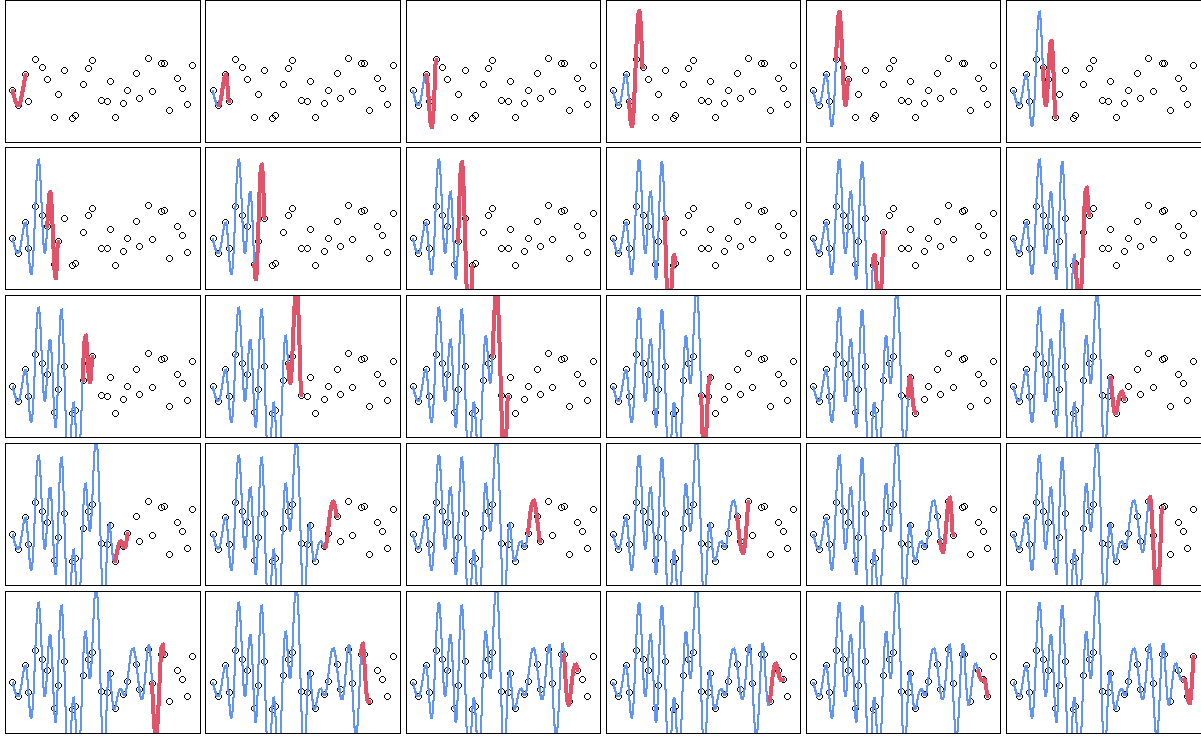
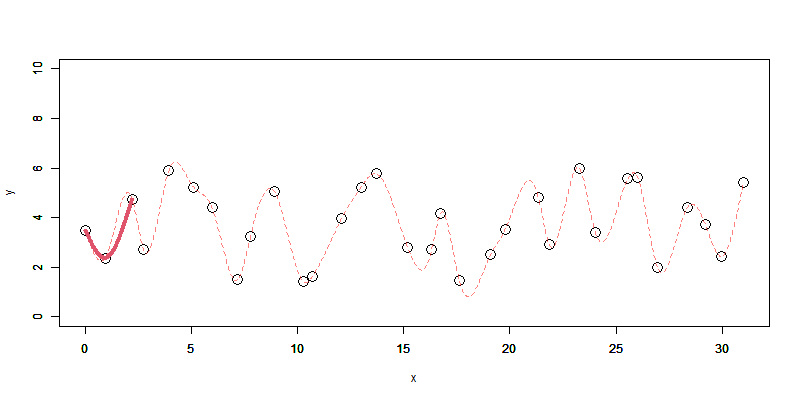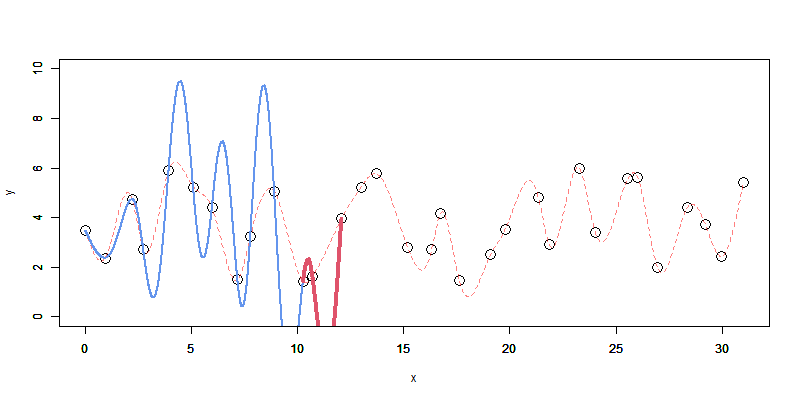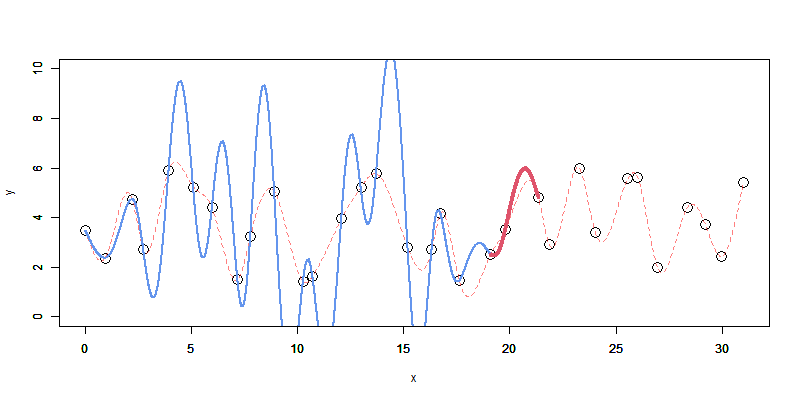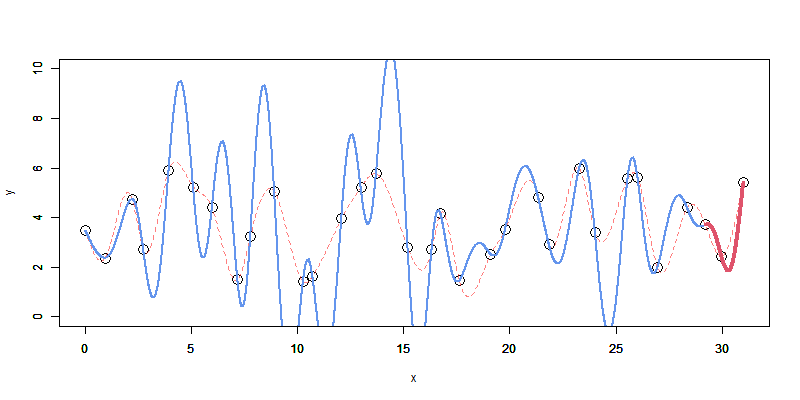
こちらで書いた１～５を先に御覧になると分かりやすいかも、です。

スプライン補間について（その１）
スプライン補間について（その２）
スプライン補間について（その３）
スプライン補間について（その４）
スプライン補間について（その５）

まとめはこちら

はじめに

スプライン補間について（その５）のところで、スプライン補間の為の区分多項式は、処理対象とする全区間に対し一括で求めなければいけないことを書きました。
そうしないと接続点で傾き・曲率共に不連続になってしまいました。

でもこれは結構困りまして、処理対象のデータが多いとものすごいサイズの巨大行列計算を行わなければいけなくなります。
あと私的に一番イヤなのは、逐次処理ができないのでリアルタイム時系列データには使用できません。
これ、すごく困ります。

そんなのはイヤなので、どうやったらスプライン補間をリアルタイム時系列データにも適用することができるのか、考えてやってみました。

この方法が良いとか正しいとかでは決してなくて 『一つのアイディア』 として参考にしてもらえればと思います。

尚、
ここに書いた内容を使ったことによる責任は一切負いません。
また、内容の正確さを保証もしません。
すべて自己責任でお願いします。
あらかじめご了承ください。

「スプライン補間について１～５」はかなり丁寧に書いたつもりです。
なので今回は 「読んで頂いているからスプライン補間のある程度の理解はある」 という前提に立って書いていこうと思います。

今回の目標

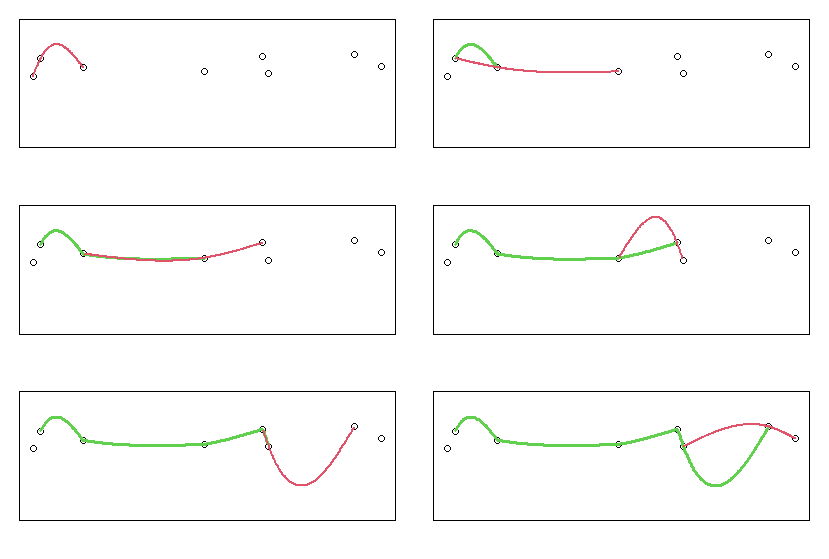
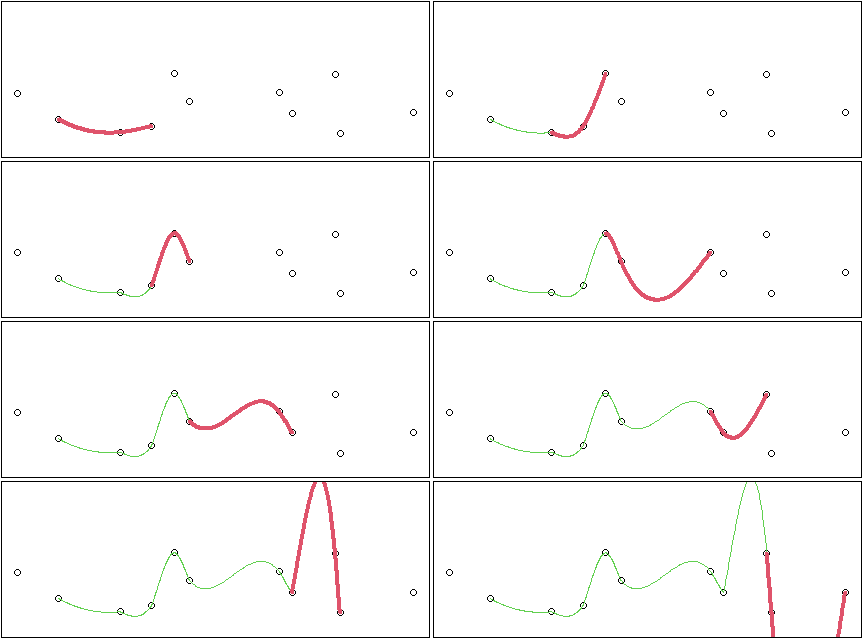
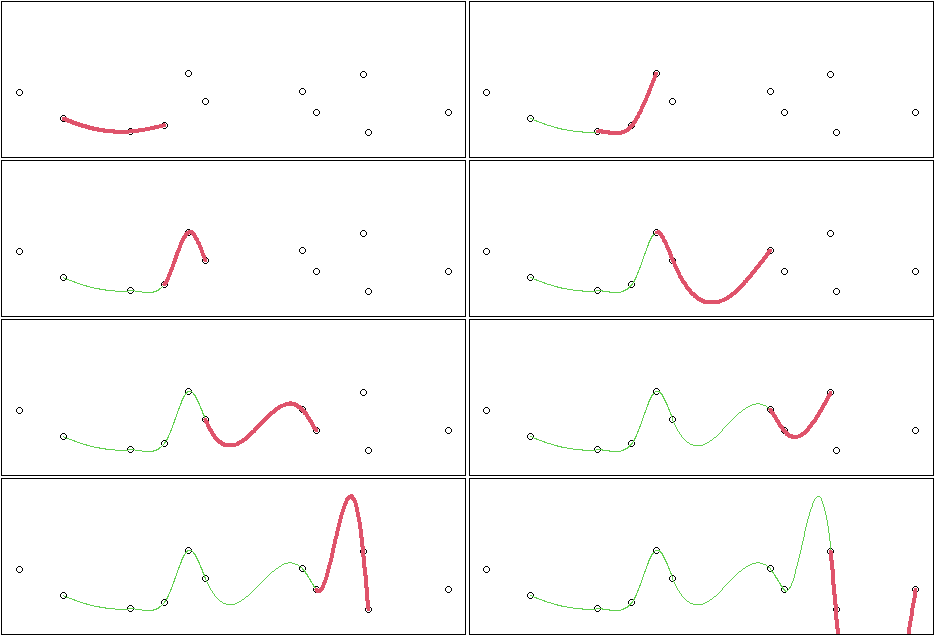
こんな感じで、次々に入ってくるデータに対して逐次でスプライン補間を適用できるようにする。

課題解決への試行錯誤

接続点での不連続

先に書いた通り、３次元スプライン補間を小区間に分割して実行すると、隣の小区間との接続点で不連続が発生します。

これは、前の区間の終点での傾き・曲率と、後区間の始点での傾き・曲率が一致していないので起こります。
ではこれを一致させることを考えます。

係数 c を合わせる

区分多項式を求めるときの始点と終点の条件を決めているのは境界条件でした。
今回は始点の値を合わせればよいので、合わせます。
前の２階微分の値と後ろの２階微分の値を合わせることになるので、

c_{\mathrm{prev}} + 3d_{\mathrm{prev}}{\Delta x_{\mathrm{prev}}} = c_{\mathrm{next}}

となります。
実際には直前の２階微分の値を保存しておいて、次の始点の境界条件に与えてやります。
（境界での２階微分の値は本当は $2c$ です。両辺２で割って使用します）

\begin{bmatrix}
\vdots & \vdots & \vdots & \vdots & \cdots & \\
0 & 0 & 1 & 0 & \cdots \\
\vdots & \vdots & \vdots & \vdots & \cdots & \\
\end{bmatrix}
\begin{bmatrix}
\vdots \\
c_{0} \\
\vdots
\end{bmatrix}
=
\begin{bmatrix}
\vdots \\
(\frac{d^2}{dx^2}/2) \\
\vdots
\end{bmatrix}

単純にn点ごとに求めたものをつなぎ合わせた場合、終点の２階微分はゼロに予め設定されているので、既に合っています。
その結果は既にみたとおり、

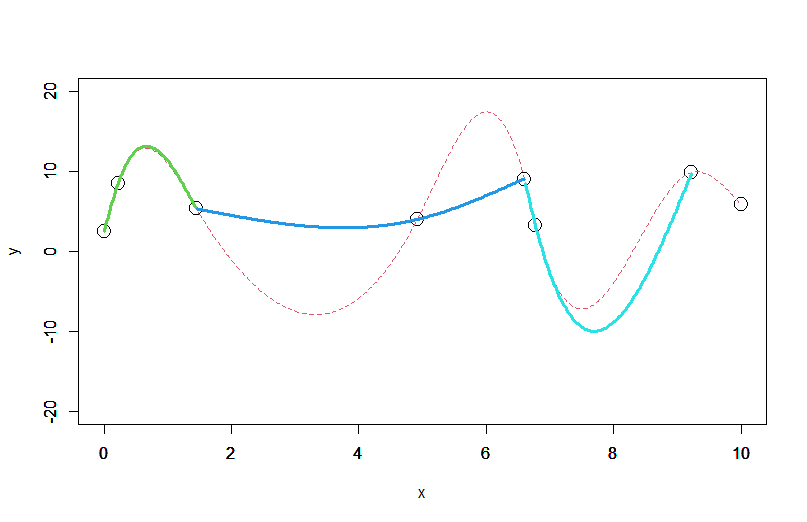
と接続点で傾きが不連続になります。

移動ウィンドウ法で c を合わせた場合は以下になります。

$p_2, p_7$ あたりが分かりやすいですが、全点で傾き（１階微分値）が一致しておらず不連続になっています。
実際の値は以下になります。

	$\rightarrow p_1$	$p_1 \leftarrow$	$\rightarrow p_2$	$p_2 \leftarrow$	$\rightarrow p_3$	$p_3 \leftarrow$	$\rightarrow p_4$	$p_4 \leftarrow$	$\rightarrow p_5$	$p_5 \leftarrow$	$\rightarrow p_6$	$p_6 \leftarrow$	$\rightarrow p_7$	$p_7 \leftarrow$	$\rightarrow p_8$	$p_8 \leftarrow$
$S'$	-1.2928	-1.5560	0.2843	-1.3687	3.9970	7.7747	-0.0131	-0.5856	-6.4686	-2.9233	-3.4282	-4.2839	-3.2528	14.3782	-29.9524	-31.0661
$S''$	1.3519	1.3519	1.0161	1.0161	12.3908	12.3908	-39.6093	-39.6093	8.9503	8.9503	-9.3964	-9.3964	15.7044	15.7044	-97.0105	-97.0105

２階微分の係数 c を合わせても、傾きまでは一致してくれないのが分かります。
また、傾きが合っていないということは、曲率も不連続で一致していないことがわかります。
（曲率の式に一階微分が入っているため）

結果、接合点の前後で c を合わせてもダメ と分かりました。

係数 b を合わせる

では傾きを合わせたら問題は解決するでしょうか。

\begin{eqnarray}
\frac{d}{dx}S_{j}(x) &=& b_j + 2c_j(x-x_j) + 3d_j(x-x_j)^2 \\
\frac{d}{dx}S_{j}(x_j) &=& b_j
\end{eqnarray} 

なので、接合点での傾きを表すのは係数 $b_j$。

b_{\mathrm{prev}} + 2c_{\mathrm{prev}}{\Delta x_{\mathrm{prev}}} + 3d_{\mathrm{prev}}{\Delta x_{\mathrm{prev}}}^2 = b_{\mathrm{next}}

とすることになります。
同じく、実際には前の１階微分の上の値を保存して次の始点の境界条件に与えます。

\begin{bmatrix}
\vdots & \vdots & \vdots & \vdots & \cdots & \\
0 & 1 & 0 & 0 & \cdots \\
\vdots & \vdots & \vdots & \vdots & \cdots & \\
\end{bmatrix}
\begin{bmatrix}
\vdots \\
b_{0} \\
\vdots
\end{bmatrix}
=
\begin{bmatrix}
\vdots \\
(\frac{d}{dx}) \\
\vdots
\end{bmatrix}

n点ごとに求めてつなぎ合わせる場合も結果は同じなので、移動ウィンドウ法で行った場合だけを示します。

傾きを合わせたのでなめらかにはつながっているのは分かります。
しかし下に示す通り、２階微分の値は前後で一致していません。
傾きはなめらかに接続されているが、曲率は不連続を起こしていることになります。

	$\rightarrow p_1$	$p_1 \leftarrow$	$\rightarrow p_2$	$p_2 \leftarrow$	$\rightarrow p_3$	$p_3 \leftarrow$	$\rightarrow p_4$	$p_4 \leftarrow$	$\rightarrow p_5$	$p_5 \leftarrow$	$\rightarrow p_6$	$p_6 \leftarrow$	$\rightarrow p_7$	$p_7 \leftarrow$	$\rightarrow p_8$	$p_8 \leftarrow$
$S'$	-1.2928	-1.2928	0.2307	0.2307	3.6067	3.6067	0.9707	0.9707	-7.1589	-7.1589	-3.0863	-3.0863	-3.7417	-3.7417	-28.7887	-28.7887
$S''$	1.3519	0.7435	1.2169	-6.0015	14.4368	38.0867	-47.2998	-52.2323	9.8651	16.1323	-12.5343	-21.0589	17.0493	80.0370	-125.9754	-154.5747

１階微分の係数 b を合わせても、２階微分値までは一致してくれません。

結果、接合点の前後で b を合わせてもダメ と分かりました。

係数 b と c を合わせる

どちらか片方だけ合わせてもダメだと分かりました。
１階微分と２階微分を合わせれば傾きと曲率を両方とも合わせることができるので、今度は係数 b と c の両方を境界条件で合わせてみます。

３次スプライン曲線を求める条件の中で、境界条件を指定できるのは最後の２つの式だけでした。
ちょうど合わせる量が２つなので、この２つの境界条件を前の１階、２階微分の値と合わせることに使用します。

\begin{bmatrix}
\vdots & \vdots & \vdots & \vdots & \cdots & \\
0 & 1 & 0 & 0 & \cdots \\
0 & 0 & 1 & 0 & \cdots
\end{bmatrix}
\begin{bmatrix}
\vdots \\
b_{0} \\
c_{0} \\
\vdots
\end{bmatrix}
=
\begin{bmatrix}
\vdots \\
(\frac{d}{dx}) \\
(\frac{d^2}{dx^2}/2) \\
\vdots
\end{bmatrix}

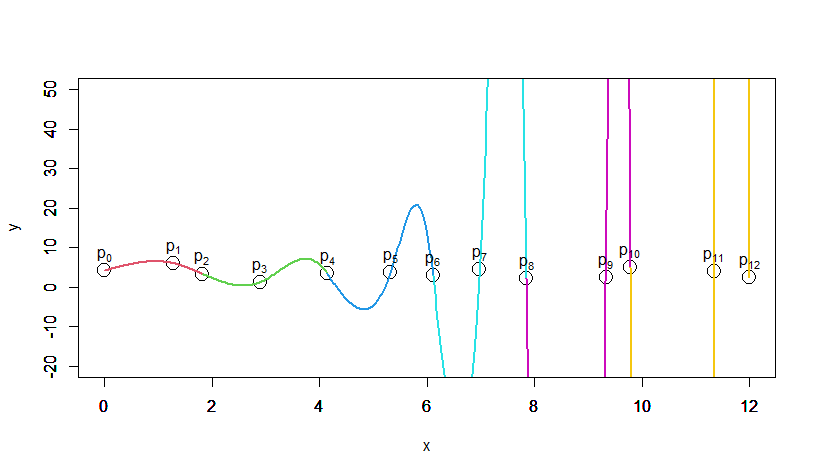
１階、２階微分の値を合わせて求めた結果が以下になります。

〇３点ごとに区切って求めつなぎ合わせた場合

〇移動ウィンドウで実施した場合

	$\rightarrow p_1$	$p_1 \leftarrow$	$\rightarrow p_2$	$p_2 \leftarrow$	$\rightarrow p_3$	$p_3 \leftarrow$	$\rightarrow p_4$	$p_4 \leftarrow$	$\rightarrow p_5$	$p_5 \leftarrow$	$\rightarrow p_6$	$p_6 \leftarrow$	$\rightarrow p_7$	$p_7 \leftarrow$	$\rightarrow p_8$	$p_8 \leftarrow$	$\cdots$
$S'$	-3.0973	-3.0973	-5.9515	-5.9515	5.8901	5.8901	-20.2309	-20.2309	78.9673	78.9673	-252.3017	-252.3017	975.9806	975.9806	-3658.3762	-3658.3762	$\cdots$
$S''$	-10.6516	-10.6516	0.0000	0.0000	22.0252	22.0252	-63.7191	-63.7191	232.0283	232.0283	-1075.1451	-1075.1451	3907.0995	3907.0995	-14567.4960	-14567.4960	$\cdots$

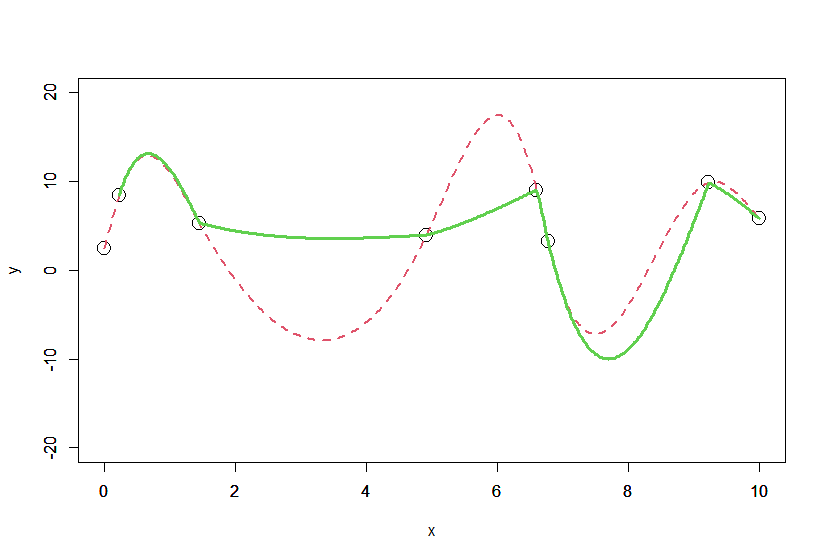
２つの結果を見てみると、１階、２階微分の値を合わせたことにより接合点で傾き・曲率が一致して、なめらかに接続されていることがわかります。

しかし、後ろに行くほど大きく上下に振動していることが見て取れます。
これは、傾きの値がどんどん大きくなってしまっていることを意味します。
また、曲率も同じくどんどん大きくなってしまっています。

残念ながら、これでは使い物になりません。

結果、接合点の前後で b と c を合わせても使い物にならない と分かりました。

発散する理由

発散する理由を考えます。
移動ウィンドウ法の場合で見ていきます。

例としてこのスプライン曲線の係数 c を示します。

c	$S_0$	$S_1$	$S_2$	$S_3$	$S_4$	$S_5$	$S_6$	$S_7$	$S_8$	$S_9$	$S_{10}$	$S_{11}$
一括	0	-5.78	3.08	2.007	-1.036	-1.588	4.212	-5.092	1.237	4.713	-5.672	0.6844

これに対して、このデータに先ほどの移動ウィンドウ法でスプライン繋ぎをしていった場合の c はこちらです。

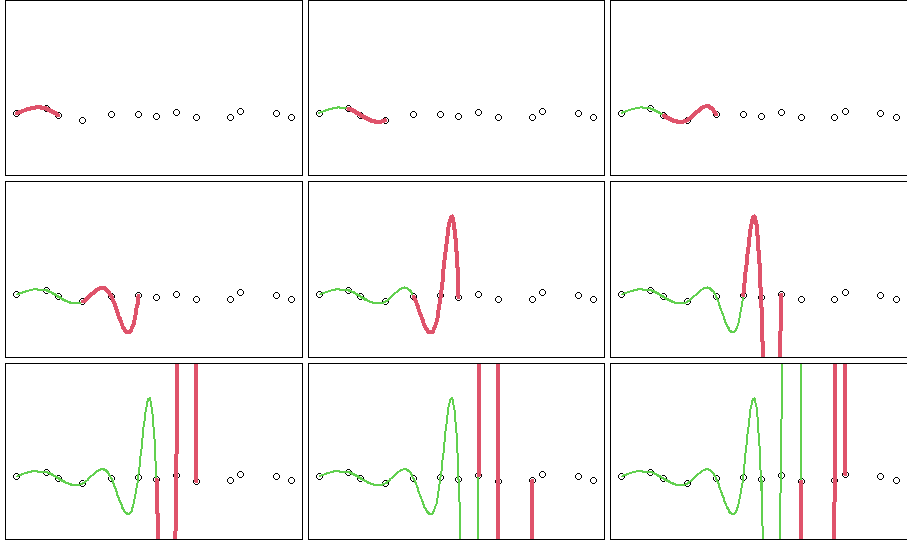
c	$S_0$	$S_1$	$S_2$	$S_3$	$S_4$	$S_5$	$S_6$	$S_7$	$S_8$	$S_9$	$S_{10}$	$S_{11}$
一括	0	-5.78	3.08	2.007	-1.036	-1.588	4.212	-5.092	1.237	4.713	-5.672	0.6844
移動	0	-5.326	0	11.01	-31.86	116	-537.6	1954	-7284	22001	-165467	418999

$S_5$ 以降急激に値が発散していっています。

これは、スプライン補間について（その２）の別解 で注意したことが起きています。

３点の移動ウィンドウで補間していっているので、最初の点 $p_1$ での係数 c は前に書いた通り以下で計算できます。

c_1 = \frac{1}{2(\Delta x_1 + \Delta x_0)} \left \{ \frac{3(y_2 - y_1)}{\Delta x_1} - \frac{3(y_1 - y_0)}{\Delta x_0} \right \}

最初の３点 $p_0, p_1, p_2$ だけで求めたスプライン曲線においては、$c_0=0, c_2=0$ だからです。
この $c_1$ を、次の１点だけずらした３点 $p_1, p_2, p_3$ でスプライン曲線を求めるときの （$p_1$ においての） 初期境界条件 $c_0$ に合わせるわけです。
これを次々行っていくわけですから、つまりこれは初期値

\begin{eqnarray}
c_0 &=& 0 \\
c_1 &=& \frac{1}{2(\Delta x_1 + \Delta x_0)} \left \{ \frac{3(y_2 - y_1)}{\Delta x_1} - \frac{3(y_1 - y_0)}{\Delta x_0} \right \}
\end{eqnarray}

において、連続３項の関係式

{\Delta x_j}c_j + 2(\Delta x_{j+1} + \Delta x_j)c_{j+1} + {\Delta x_{j+1}}c_{j+2} = \frac{3(y_{j+2} - y_{j+1})}{\Delta x_{j+1}} - \frac{3(y_{j+1} - y_{j})}{\Delta x_{j}}

を用いて $c_j$ を次々求めていくことと同じになります。
これを行うと上に示した結果の通り発散していきます。
これは既に 「スプライン補間について（その２）の別解」 で注意した通りです。

尚、この連続３項の関係式は、一括で求めた時の $c_1$ （上の場合は -5.78 ）を代入して計算していけば、発散せずに正しく行列計算の時と同じ値を導き出します。
なので、この連続３項の関係式に問題はありません。

発散してしまう理由を考えます。

変更したところはどこだったかを思い出すと、境界条件 でした。
求解時の境界条件において、始点での１階と２階微分の値を指定するために 終点の境界条件を指定していない 状態になっています。
指定できる境界条件の式は２つしかなく、その２つの式を始点の条件に使ってしまったためです。
これによって終点の条件がないことになり、終点側がどんどん発散していくことになってしまっています。

これはいわば始点だけ結んでいる終端を固定していないロープが、風で自由にたなびいている状態に似ています。

これが値が発散して曲線が大きく上下に振れてしまう理由です。
これを回避するには、終点も境界条件によって拘束しなければなりません。

始点と終点の境界条件を指定する

３次スプライン曲線を求めるにあたって、必要とした条件は以下でした。
そして、それぞれの条件で必要とする式の数は以下です。

　１．曲線の連続性（ 2n 個 )
　２．傾きの連続性（ n-1 個）
　３．曲率の連続性（ n-1 個）
　４．境界条件　　（ 2 個）

合わせて 4n 個、係数の数と一緒です。
ここから分かる通り、４．境界条件を指定する式は２つしかありません。
始点の境界条件で２つ使うので、終点の境界条件を指定するには３つ以上の式が必要です。
しかし、4n 個の係数を求める為に 4n+1 個以上の式を立てると求解不能になります。
とはいえ、１～３の条件式どれか一つが欠けるとデータ点で不連続が発生してしまいます。
なので 3n-2 個の式から一つ拝借することもできません。

これは連立方程式を与える動かせない条件なので、残念ですが３次多項式の範囲で考えても答えはでません。

そこで、次数をひとつ上げてみます。

４次多項式のスプライン曲線なら、境界条件を 3 個指定することができます。

平面曲線を求めるのに４次多項式を用いることの是非はいったん置いておきましょう。
３つのうち２つを始点の境界条件に、１つを終点の境界条件に使います。
始点では１階微分と２階微分の値を前と合わせ、終点では２階微分の値をゼロとします。

\begin{bmatrix}
\vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 3\Delta x & 6{\Delta x}^2
\end{bmatrix}
\begin{bmatrix}
\vdots \\
b_{0} \\
c_{0} \\
\vdots 
\end{bmatrix}
=
\begin{bmatrix}
\vdots \\
(\frac{d}{dx}) \\
(\frac{d^2}{dx^2}/2) \\
0
\end{bmatrix}

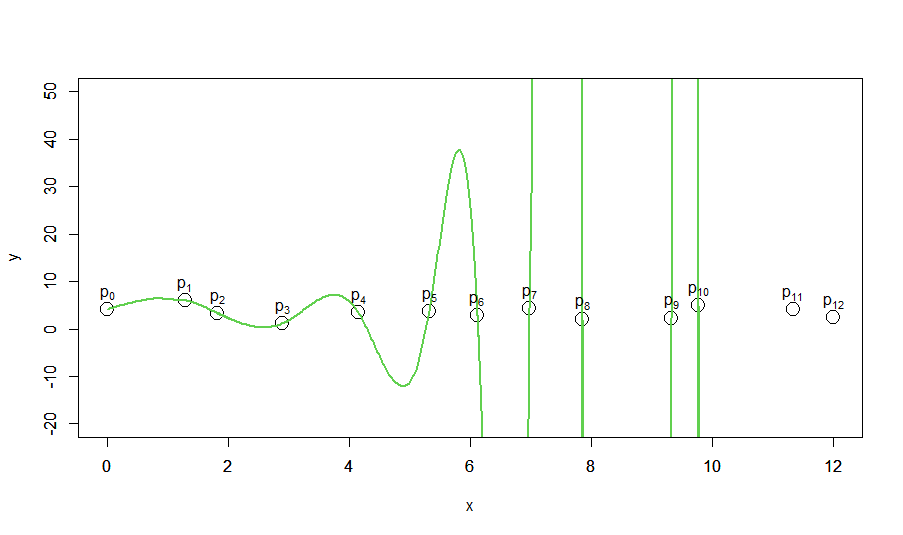
そうやって移動ウィンドウで求めた結果が以下です。

	$\rightarrow p_1$	$p_1 \leftarrow$	$\rightarrow p_2$	$p_2 \leftarrow$	$\rightarrow p_3$	$p_3 \leftarrow$	$\rightarrow p_4$	$p_4 \leftarrow$	$\rightarrow p_5$	$p_5 \leftarrow$	$\rightarrow p_6$	$p_6 \leftarrow$	$\rightarrow p_7$	$p_7 \leftarrow$	$\rightarrow p_8$	$p_8 \leftarrow$	$\cdots$
$S'$	0.08026546	0.08026546	-0.05397315	-0.05397315	-6.43646623	-6.43646623	11.13043146	11.13043146	-10.35662050	-10.35662050	8.27055779	8.27055779	-8.77645303	-8.77645303	13.42501963	13.42501963	$\cdots$
$S''$	4.1784264	4.1784264	-13.1648592	-13.1648592	-0.6855106	-0.6855106	-3.9236490	-3.9236490	6.1215285	6.1215285	4.9060681	4.9060681	26.2289469	26.2289469	14.8333080	14.8333080	$\cdots$

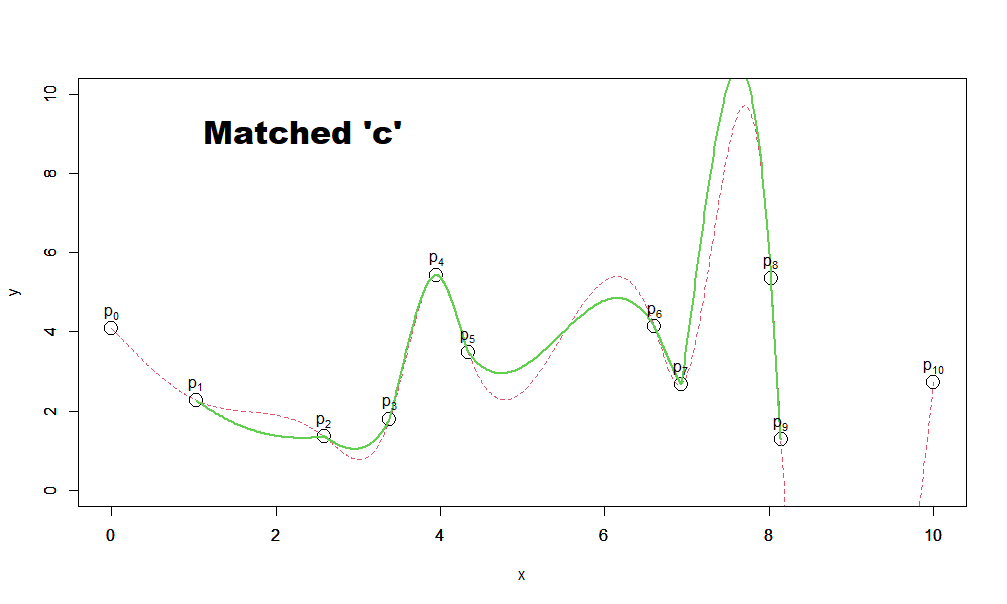
今度は１階、２階微分の値も一致してなめらかに線が繋がり、かつ発散もせずデータ点をつないでいってくれています。

ここまでの結果より、スプラインでデータ点を接続していくには境界条件において

　〇　接合点前後の微分の値を合わせる
　〇　（逐次においての）終端の境界条件を設定する

ことが必要であることが分かりました。

以上で、発散させずにデータ点をなめらかに逐次で補間していく方法を見つけることができました。
目的達成です。

目的は達成したが・・・

ここまでで、

　〇　逐次補間に使用する多項式を ”４次多項式” にする
　〇　係数求解時の境界条件にて、
　　　　１．接続点での１階微分値を合わせる
　　　　２．接続点での２階微分値を合わせる
　　　　３．終点での２階微分値をゼロに設定する

という方法をとることで、逐次スプライン補間を続けていくことができることがわかりました。

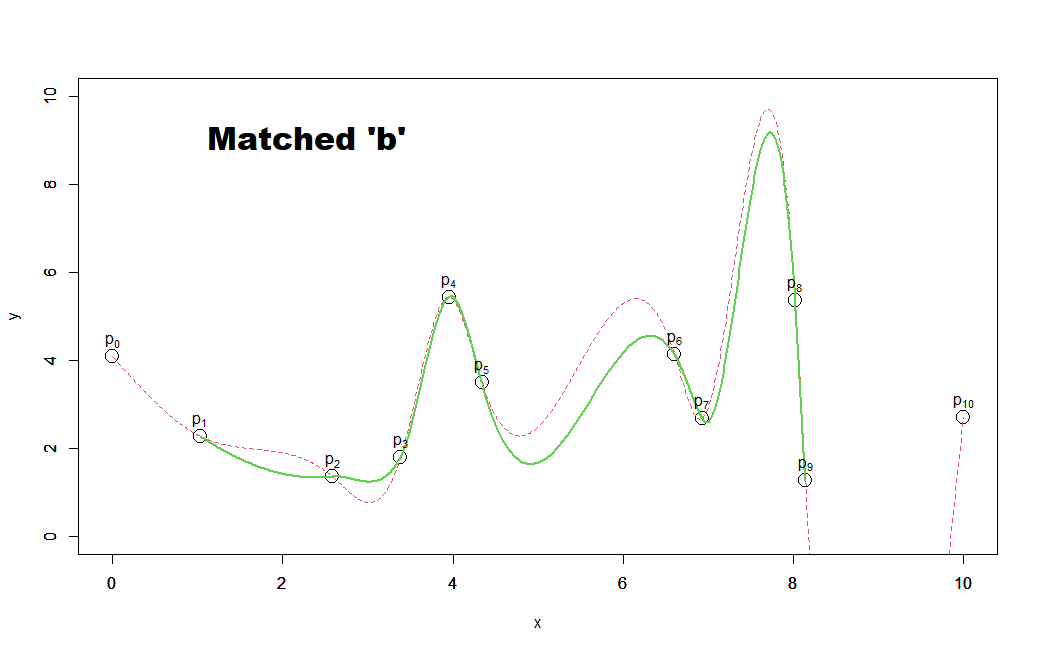
しかし、上のグラフで赤の点線で示した元々の３次多項式のスプライン曲線(全範囲で一括)とは結構形が変わってしまっています。
また、平面曲線を求めるにあたって４次多項式を使用することの是非も未検証のままです。

目的は達成しましたが、これで本当に使い物になる妥当な方法が得られたのか疑問です。
もうすこし工夫してもともとの赤の点線の３次スプライン曲線に近づけることはできないでしょうか？

まだもうすこし検証が必要です。

つづく

今回もまた長くなってしまったので、いったんここまでで投稿します。
最初に示した次々補間していっているアニメーションは、この４次多項式を使った方法ではなく、ちゃんと上の新しい課題を克服した方法で補間をした結果のアニメーションになります。

その方法は次回書こうと思います。

よろしくお願いいたします。

こちらに続きます
時系列逐次スプライン補間の実践（後編）

【結果先取】