はじめに
サンプリングデータを扱っていると、手元のデータからアップサンプリングしたい時があります。
また別の動機として、サンプリングデータのサンプリング間隔が一定でない場合に間隔を揃えたい、つまり間隔が不揃いなデータから一定間隔のサンプリングデータを推測したいということがあります。
時間間隔一定でないと、フーリエ変換とかできませんからね。
そんな時に値と値の間を3次多項式で表して、その3次多項式からデータ点間の値を取って使おうという手法があります。
3次スプライン曲線を使った、3次スプライン補間です。
今回はこの 3次スプライン補間 の話を書いていきます。
最近の流行りは、誰かが作ったライブラリをどう使うか、その使い方を知るのが大事で、その理論や数式知ってどうするの？って感じだなぁと思っています。
しかし、そういうものを使うにしても、中を分かって使うのか、ブラックボックスで使うのかでは応用や質の面で全然違った結果になると思います。
なので、ライブラリの使い方や数式の表面をサラッと流すようなことを書くのではなく、ちゃんと理論と中身を書いていきたいと思います。
なので、3次スプライン補間に関して
・手っ取り早く使い方を知りたい
・コード書く為に結果の式だけ知りたい
って方は別の方の書かれた記事参照されたほうが早いしわかりやすいと思います。
私はせっかくなので、ここでは他の方があまり書いていないことを書いてみようと思います。
書くつもりの目次
- スプラインの意味
- 導出
- ３次の理由
- 1次、2次の場合
- 4次以上の場合
- 空間内の運動への適用
- 2次元平面
- 3次元空間
- 高次空間
- 使用にあたっての注意
- 一括適用と逐次適用
- y=f(x)にパラメータ手法を適用した場合
これを一つの記事で書こうと思って書いていたのですが、あまりに長くなって重くなってしまったので、複数回に分けることにしました。
ページ遷移の面倒くささがあると思いますが、ご容赦ください。
だいぶ長くなってしまいましたが、全部書けました。
結論だけ先に知りたい方はこちらの（まとめ）からどうぞ。
1．そもそも "スプライン" って何？
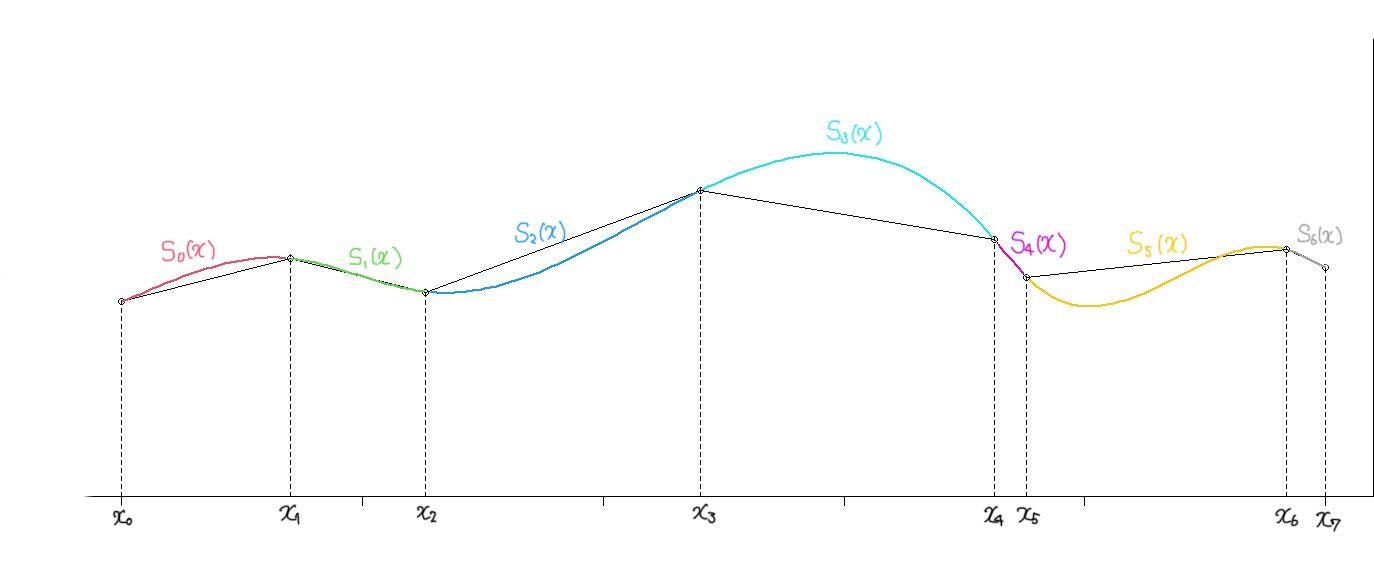
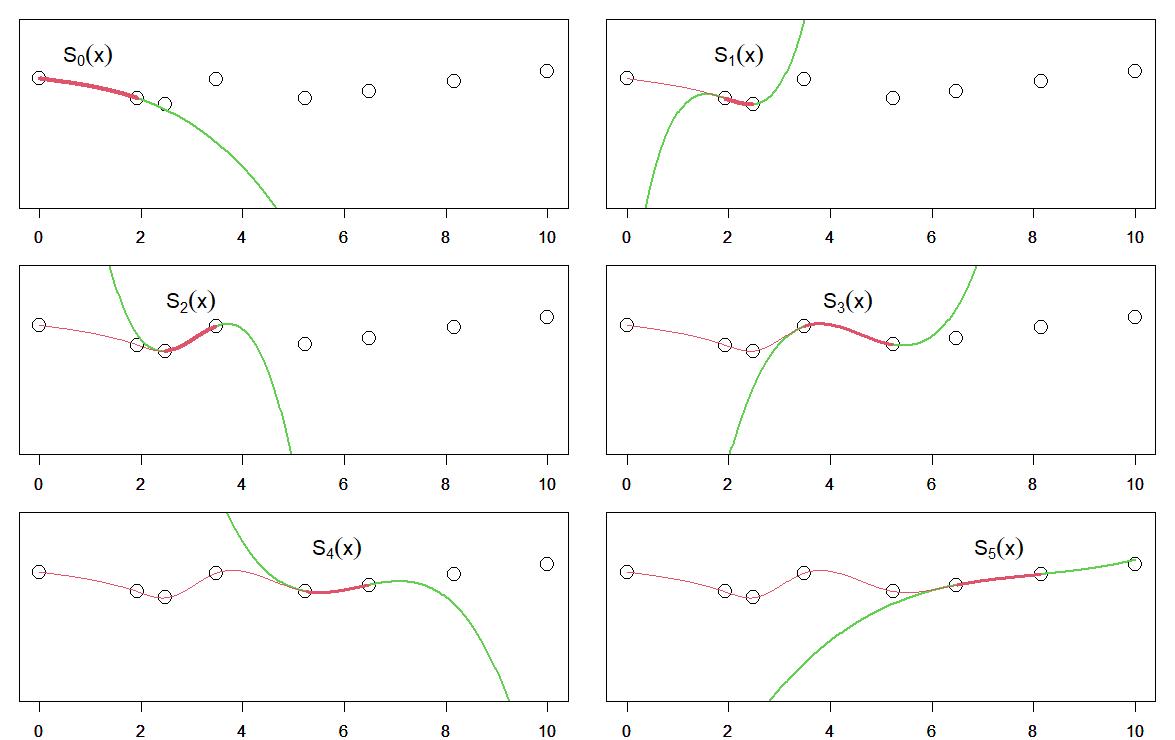
スプラインとは 区分的に定義された多項式（区分多項式） で表される関数の事。
普通、各データ点を通る関数を求めようとするとき、全データ点を通るある一つの関数 $f(x)$ を求めようとすることが多いです。
これに対してスプラインは、データ点で区切られる区間ごとに異なる多項式の関数を求めます。
データ$(x_1, y_1)$とデータ$(x_2, y_2)$の間は$S_1(x)$ 、次のデータ $(x_2, y_2)$ とデータ $(x_3, y_3)$ の間は $S_2(x)$ といったように。
つまり、
S(x) = \left\{
\begin{matrix}
S_0(x) & x_0 < x \leq x_1 \\
S_1(x) & x_1 < x \leq x_2 \\
S_2(x) & x_2 < x \leq x_3 \\
\vdots
\end{matrix}
\right.
といった具合に、区間ごとに異なる関数をつなぎ合わせていくイメージです。
こっちの方が分かりやすいですかね。
そしてこの区間ごとに異なる関数には、多項式を使います。
\begin{eqnarray}
S_0(x) &=& a_0 + b_0 x + c_0 x^2 + d_0 x^3 \\
S_1(x) &=& a_1 + b_1 x + c_1 x^2 + d_1 x^3 \\
S_2(x) &=& a_2 + b_2 x + c_2 x^2 + d_2 x^3 \\
&\vdots&
\end{eqnarray}
式の形は同じですが、係数が違います。
以下、区分多項式を $S_j(x)$ で表すこととします。
また、多項式の形は後で少し変形します。
さらに詳しいことはWikipediaや専門に解説しているところを参照ください。
２．導出の為の条件の確認
まずはコマゴマしたことを後回しにして、導出のための条件を確認しに行きましょう。
まぁ、コマゴマしたことの方が面白いんですが。
それはあとでのお楽しみとします。
導出に使う条件
他で書かれているのと同じく、ここでのスプライン曲線はすべて3次とします。
つまり、3次スプライン曲線を求めます。
（3次以外の場合の話は後程）
この場合、使う条件は以下の4つです。
[1] 関数のつなぎ目、つまり各データ点での前後2つの関数の値は同一であり $y$ と一致する
[2] 同じく、各データ点での前後2つの関数の一階微分の値は一致する
[3] さらに、各データ点での前後2つの関数の二階微分の値も一致する
[4] 両端のデータ点での二階微分の値は０である
ひとつずつみていきます。
注意。
データ点は $0～n$ までの $(n+1)$個ある想定です。
スプラインの多項式はその間の区間の数だけあるので、$S_0$～$S_{n-1}$ までの $n$個です。
多項式$S_j(x)$の$j$は、区間内の一番小さい$x$、つまり左側のデータ点の番号$j$を使います。
【例】
区間 $x_0$と$x_1$の間の多項式は$S_0(x)$
区間 $x_j$と$x_{j+1}$の間の多項式は$S_j(x)$
１．各データ点での前後2つの関数の値は同一でありy と一致する
これは 関数の連続性 を担保するための条件です。
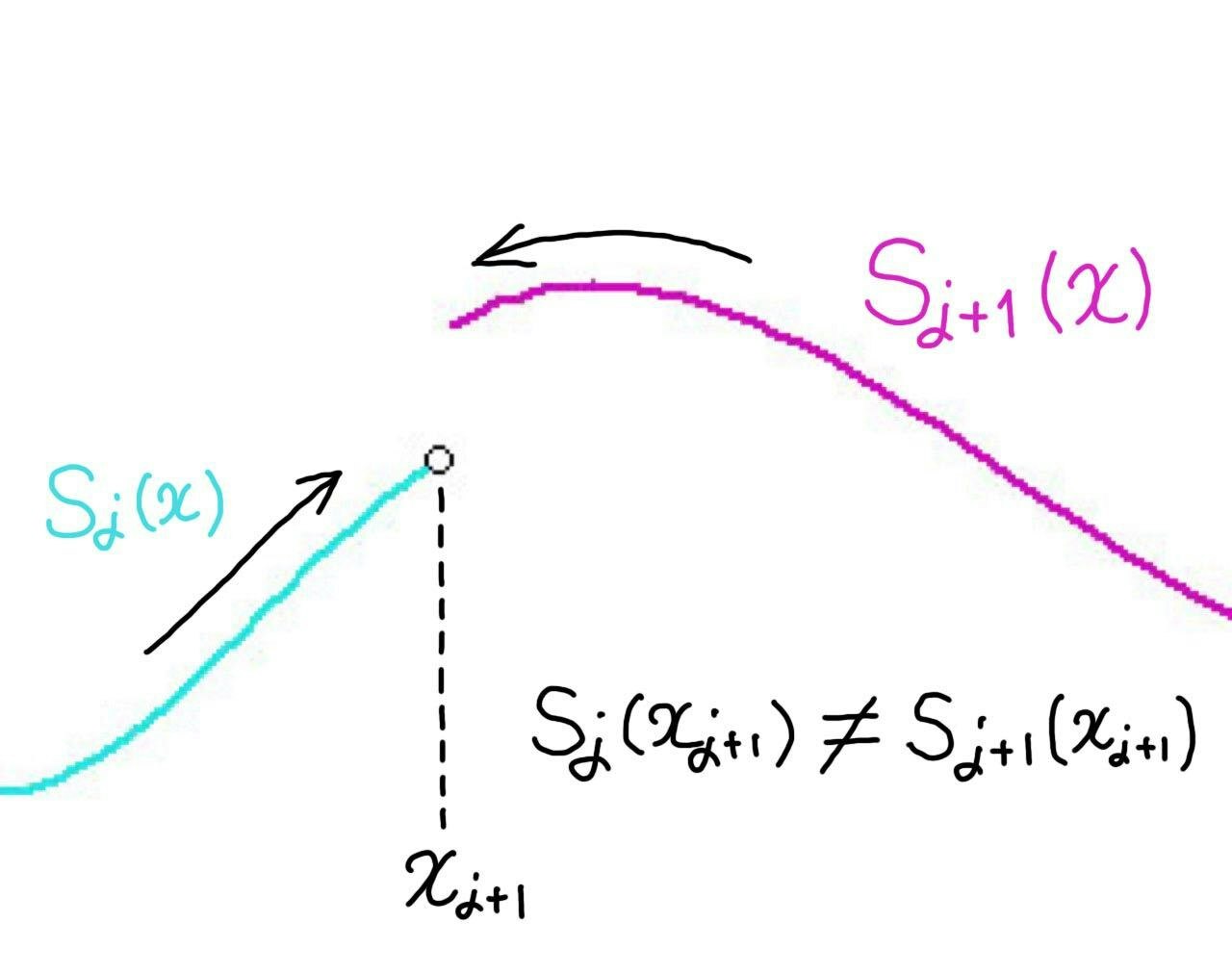
あるデータ点に対して、右から近づいた時と左から近づいた時で値が違っていたら、そこで線が途切れることになるので困ります。
左から $x_{j+1}$ に近づいた時 $y$ の値は $y=S_j(x_{j+1})$、右から近づいた時は $y=S_{j+1}(x_{j+1})$。
この図の場合は $S_j(x_{j+1}) \neq S_{j+1}(x_{j+1})$。
なので $x_{j+1}$ で不連続になっている。
また、そのデータ点 $x_n$での $y$ の値は $y_n$ ですから、両方の関数に $x_n$ を入力したら同じ $y_n$ が出てきてくれないと困ります。
式で書けばこういうことです。
\begin{eqnarray}
S_0(x_1) &=& S_1(x_1) = y_1 \\
S_1(x_2) &=& S_2(x_2) = y_2 \\
S_2(x_3) &=& S_3(x_3) = y_3 \\
&\vdots& \\
S_j(x_{j+1}) &=& S_{j+1}(x_{j+1}) = y_{j+1}\\
\end{eqnarray}
データ点の前後の関数 $S_j(x)$と$S_{j+1}(x)$ において、データ点$x_j$での値が等しくなっています。
これは、線が途切れずつながっていることを意味しています。
いまはデータをなめらかにつなぐ関数が欲しいわけなので、関数の連続性を担保するこの条件が必要なことが分かると思います。
２. 各データ点での前後2つの関数の一階微分の値は一致する
この条件は 関数がなめらかに繋がっていること を担保するための条件です。
関数の一階微分は接線の傾きを表しますから、この条件は左右両関数（$S_j(x)$と$S_{j+1}(x)$のこと）のデータ点での接線が一致することを要求しています。
接線が一致しない場合、関数は連続でもその点で関数が折れ曲がったように滑らかにつながりません。
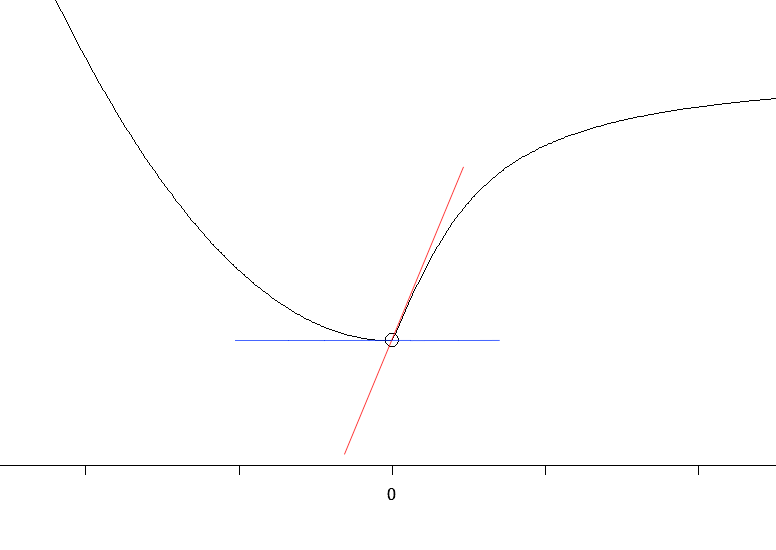
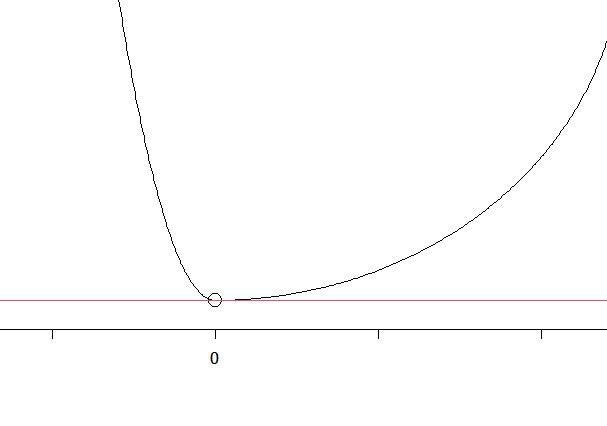
左側からの接線と右側からの接線が一致しない場合の例。
左側から近づいた場合の接線が青、右側から近づいた接線を赤で示している。
$x=0$ で関数は連続、つまり途切れずつながっているが、 $x=0$ の点で折れ曲がっており、なめらかではない。
数学的には $x=0$ で微分不可 である。
数式で書けば以下です。
\begin{eqnarray}
S_0'(x_1) &=& S_1'(x_1) \\
S_1'(x_2) &=& S_2'(x_2) \\
S_2'(x_3) &=& S_3'(x_3) \\
&\vdots& \\
S_j'(x_{j+1}) &=& S_{j+1}'(x_{j+1})
\end{eqnarray}
$S'(x)$ は $S(x)$の微分、$S'(x)=\frac{d}{dx}S(x)$ です。
これで関数がなめらかに繋がっていることが担保されます。
３．各データ点での前後2つの関数の二階微分の値も一致する
この条件は左右で曲がり具合が一致することを担保するためにあります。
正確に言えば、データ点で左右両関数の 曲率 が一致することを要求しています。
「急に曲がり方が変わったりしない曲線であってください」ということです。
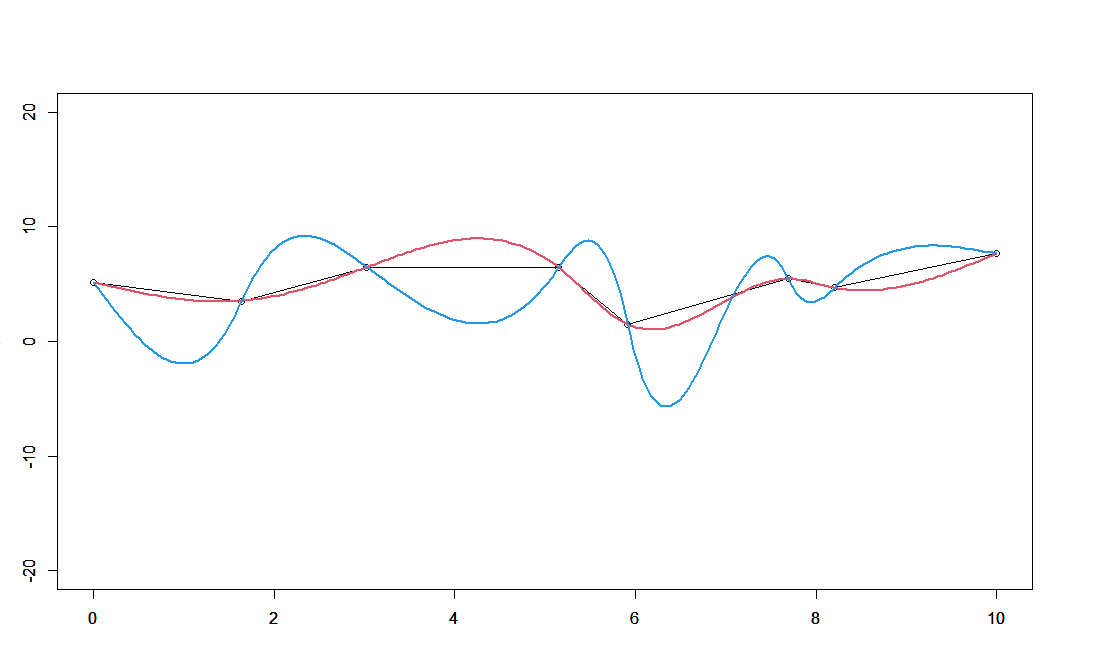
曲率が不連続な例。
$x=0$ で曲線は連続的に接続されており、接線も左右どちらからでも傾き０であり一致する（赤の線）。
つまりこのグラフの関数は連続関数でありかつなめらか。
しかり曲がり具合が $x=0$ を境にして左右で異なっている。
人によってはこれは「見た感じ問題ないじゃないか」と思う人もいると思います。
それも一つの考え方なので、そういう方はこの条件を外せばよいです。
これは「曲率がこのデータ点で不連続に変化してもよい」という立場に立つことになります。
３次元スプライン補間においては、「自然現象は連続的に変化しある点で不連続な変化を起こさない」という考えに立って補間を考えるので、曲がり具合も連続的にしか変化しないことを要求しています。
数式で書けばこの条件はこのようになります。
\begin{eqnarray}
S_0''(x_1) &=& S_1''(x_1) \\
S_1''(x_2) &=& S_2''(x_2) \\
S_2''(x_3) &=& S_3''(x_3) \\
&\vdots& \\
S_j''(x_{j+1}) &=& S_{j+1}''(x_{j+1})
\end{eqnarray}
各データ点での左右両関数の二階微分の値を一致させていますね。
さて。
他のところではこのようにサラッと流してしまっていますが、実はこれでは話が飛んでいます。
"曲率を一致させるために、二階微分の値を一致させる"
なぜ？
関数の二階微分は曲率ではないのに？
これをちゃんと書いているところは私が探した限り見つけられませんでした。
以下、説明します。
$y=f(x)$ で表される関数の点 $a$ での曲率 $\kappa(a)$ は以下で計算されます。
\kappa(a) = \frac{|{f''(a)|}}{ (1+f'(a)^2)^{\frac{3}{2}} }
これの導出も面白いのですが、ここで書くと長くなる上にスプラインの話から離れるので、別の方が書かれているページにお任せします。
やりたいことは、
データ点の左側関数$S_j(x)$から計算される曲率$\kappa_{j}(x)$ と右側関数 $S_{j+1}(x)$ から計算される $\kappa_{j+1}(x)$ を、データ点 $x_{j+1}$ において一致 $\kappa_{j}(x_{j+1}) = \kappa_{j+1}(x_{j+1})$ させたい
です。
この曲率は分数になっているので、分母と分子がそれぞれ一致すればよいですね。
まず分母ですが、$f'(a)^2$ と１が＋でつながっているので、必ず０以上 $(1+f'(a)^2)^{\frac{3}{2}} > 0$ です。
さらにひとつ前の条件（２つ目の条件）において、データ点での前後関数の一回微分の値は同じであること $S_j'(x_{j+1}) = S_{j+1}'(x_{j+1})$ を要請しているので、前後の関数でこの分母の値は同一になります。
(1+S_{j}'(x_{j+1})^2)^{\frac{3}{2}} = (1+S_{j+1}'(x_{j+1})^2)^{\frac{3}{2}}
分母が一致したので、今度は分子です。
分子は関数の二階微分の絶対値になっていますので、
S_j''(x_{j+1}) = S_{j+1}''(x_{j+1})
であれば両方の曲率が一致することが分かります。
つまり、左右両方からのの曲率を一致させるための条件は
前後両関数 $S_j(x)$と$S_{j+1}(x)$の二階微分の値を、データ点 $x_{j+1}$ で一致させればよい
ということが分かりました。
これをまとめると、先に示した条件式になります。
【再掲】
\begin{eqnarray}
S_0''(x_1) &=& S_1''(x_1) \\
S_1''(x_2) &=& S_2''(x_2) \\
S_2''(x_3) &=& S_3''(x_3) \\
&\vdots& \\
S_j''(x_{j+1}) &=& S_{j+1}''(x_{j+1})
\end{eqnarray}
これが３つ目の条件が二階微分の値を同一にすることを要求していることの意味です。
これで曲がり方においてもなめらかに関数がつながることが担保されました。
お気づきのように、分子が一致するためには絶対値が一致していればよく、この条件式のように正負まで含めて一致している必要はありません。
なので、
$S_j''(x_{j+1}) =-S_{j+1}''(x_{j+1})$
でも曲率は同じになり条件を満たします。
が、「曲がり方も連続的に変化」の ”趣旨” は満たしません。
なぜでしょう？
ちなみに、正負逆で一致する上の条件の場合にどうなるかはこちら。
赤が正負含めて一致させた場合。
青が正負逆転して一致させた場合。
なぜこうなるのか、何が起こっているのか考えてみると面白いと思います。
４．両端のデータ点での二階微分の値は０である
実はこの条件は絶対ではありません。
別の条件に変えても問題ありません。
いわばポリシー、流儀みたいなものです。
この条件が要請しているのは、データの両端、つまり最初のデータ点 $x_0$ と最後のデータ点 $x_n$ においては、曲率がゼロ、つまりまっすぐでありなさい、ということです。
言い換えれば、
$x_0$より前の部分では（傾きはわからないけど）まっすぐな直線で$x_0$に到達し、その後曲線になって$x_n$まで来たら、それより後の部分はまたまっすぐな直線で先に進んでいく
とういことです。
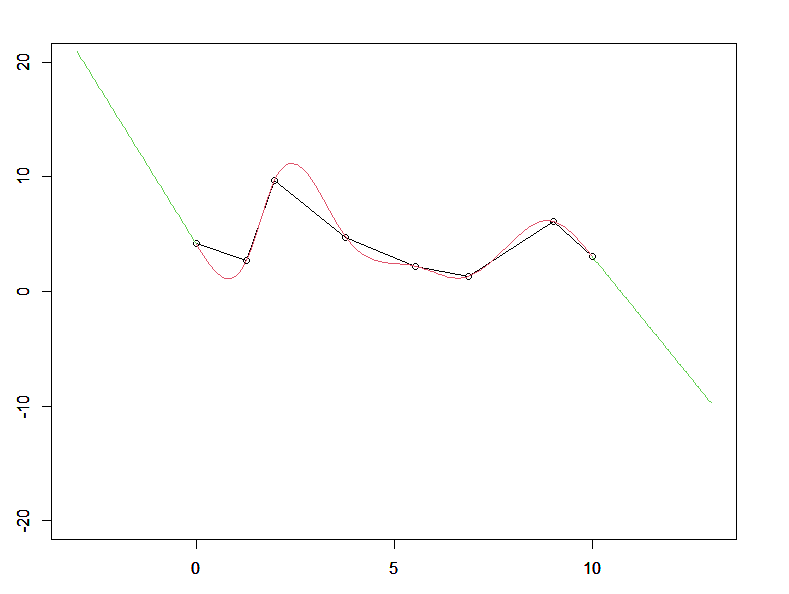
両端での曲率ゼロの例
両端データの外側、この図で両側の緑のまっすぐな直線が、両端データ点から内側の赤の曲線に滑らかにつながっている
スプライン曲線は各データ点の間で定義されるので、当然この両端の緑の線はスプライン曲線ではないです。
ただ、スプライン曲線の両側を延長したらこのような直線になるように曲線をつくってね、ということです。
この要請は、使う人の好みが分かれるところかと思います。
両端の外側をどうするか選んでこの境界条件を好みに設定すればよいかと思います。
ここではこの両端の先は直線になる条件を選択して進みましょう。
この条件の数式は以下になります。
\begin{eqnarray}
S_0''(x_0) &=& 0 \\
S_{n-1}''(x_n) &=& 0
\end{eqnarray}
曲率を表す式の分子がゼロになるので、両端で曲率がゼロになり直線につながっていきます。
おさらい
ここまでを簡単におさらいします。
与えられたすべてのデータ点を通る、自然で滑らかなスプライン曲線を得るために以下の条件を要請しました。
[1] 各データ点での前後2つの関数の値は同一であり $y$ と一致する
この条件は
・関数が全部のデータ点を通ること
・曲線が途中で途切れたりして不連続にならないこと
の為に設定されます。
[2] 各データ点での前後2つの関数の一階微分の値は一致する
この条件は、関数が途中で折れ曲がって滑らかではなくなる事がないように設定されます。
[3] 各データ点での前後2つの関数の二階微分の値は一致する
この条件は、曲線の曲がり方が連続的に変化する、いきなり曲がり方が変わったりしないように設定されます。
[4] 両端のデータ点での二階微分の値は０である
この条件は、使用する人のポリシーです。
両端の先は直線につながるという設定をしています。
この４つの条件設定の元でスプライン曲線を求めていきます。
つづく
その２に続きます。