前回まではこちら。
スプライン補間について(その1)
スプライン補間について(その2)
スプライン補間について(その3)
スプライン補間について(その4)
スプライン補間について(その5)
スプライン補間についてのまとめ
最初に書こうとした項目が全部書けたので、ここでまとめとしたいと思います。
「スプライン」の意味
「区分的に定義された多項式(区分多項式)で表される関数」 = スプライン
S(x) = \left\{
\begin{matrix}
S_0(x) & x_0 < x \leq x_1 \\
S_1(x) & x_1 < x \leq x_2 \\
S_2(x) & x_2 < x \leq x_3 \\
\vdots
\end{matrix}
\right.
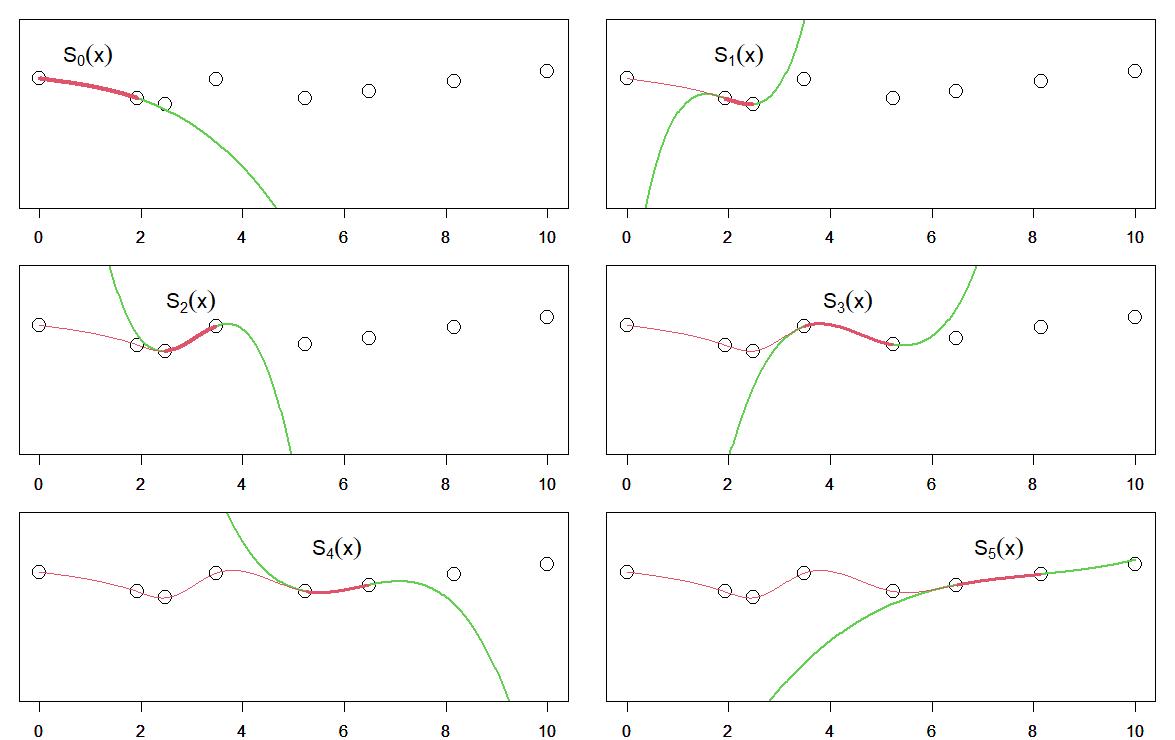
3次スプライン曲線の導出条件
1.曲線が途切れない為の条件
途中で曲線が途切れてしまわないように、データ点で曲線がちゃんと接続されているようにする。
\begin{eqnarray}
S_0(x_1) &=& S_1(x_1) = y_1 \\
S_1(x_2) &=& S_2(x_2) = y_2 \\
S_2(x_3) &=& S_3(x_3) = y_3 \\
&\vdots& \\
S_j(x_{j+1}) &=& S_{j+1}(x_{j+1}) = y_{j+1}\\
\end{eqnarray}
2.曲線が折れ曲がらない為の条件
曲線が滑らかにつながるように、データ点での曲線の傾きを一致させる。
\begin{eqnarray}
S_0'(x_1) &=& S_1'(x_1) \\
S_1'(x_2) &=& S_2'(x_2) \\
S_2'(x_3) &=& S_3'(x_3) \\
&\vdots& \\
S_j'(x_{j+1}) &=& S_{j+1}'(x_{j+1})
\end{eqnarray}
3.曲線の曲がり方が不連続に変化しないようにするための条件
データ点の前後で曲率が不連続に変化しないように、条件2と併せて曲率を一致させる。
\begin{eqnarray}
S_0''(x_1) &=& S_1''(x_1) \\
S_1''(x_2) &=& S_2''(x_2) \\
S_2''(x_3) &=& S_3''(x_3) \\
&\vdots& \\
S_j''(x_{j+1}) &=& S_{j+1}''(x_{j+1})
\end{eqnarray}
4.境界条件
任意に設定可。バリエーションがある。
今回は、最初のデータ点と最後のデータ点の外側では、スプライン曲線がなめらかに直線につながっていくように設定している。
つまり、両端で曲率がゼロ。
\begin{eqnarray}
S_0''(x_0) &=& 0 \\
S_{n-1}''(x_n) &=& 0
\end{eqnarray}
ここまでの内容は以下に書きました。
スプライン補間について(その1)
導出方法
条件を設定したら、その条件を式にして連立方程式を立てます。
区分多項式の一般系を以下に設定。
\begin{eqnarray}
S_j(x) &=& a_j + b_j(x - x_j) + c_j(x - x_j)^2 + d_j(x - x_j)^3 \\
\end{eqnarray}
求めるのは、この係数 $a_j,b_j,c_j,d_j$ 達、$4n$ 個(区間が n区間の場合)。
条件1より
\scriptsize{
\begin{eqnarray}
\begin{matrix}
S_0(x_0) & = & a_0 & + & 0 & + & 0 & + & 0 & = & y_0 \\
S_0(x_1) & = & a_0 & + & b_0(x_1 - x_0) & + & c_0(x_1 - x_0)^2 & + & d_0(x_1 - x_0)^3 & = & y_1 \\
S_1(x_1) & = & a_1 & + & 0 & + & 0 & + & 0 & = & y_1 \\
S_1(x_2) & = & a_1 & + & b_1(x_2 - x_1) & + & c_1(x_2 - x_1)^2 & + & d_1(x_2 - x_1)^3 & = & y_2 \\
& \vdots & \\
S_j(x_j) & = & a_j & + & 0 & + & 0 & + & 0 & = & y_j \\
S_j(x_{j+1}) & = & a_j & + & b_j(x_{j+1} - x_j) & + & c_j(x_{j+1} - x_j)^2 & + & d_j(x_{j+1} - x_j)^3 & = & y_{j+1} \\
& \vdots & \\
S_{n-1}(x_{n-1}) & = & a_{n-1} & + & 0 & + & 0 & + & 0 & = & y_{n-1} \\
S_{n-1}(x_{n}) & = & a_{n-1} & + & b_{n-1}(x_{n} - x_{n-1}) & + & c_{n-1}(x_{n} - x_{n-1})^2 & + & d_{n-1}(x_{n} - x_{n-1})^3 & = & y_{n} \\
\end{matrix}
\end{eqnarray}
}
条件2より
\small{
\begin{eqnarray}
\begin{matrix}
S_0'(x_1) & = & b_0 & + & 2c_0{\Delta x_0} & + & 3d_0{\Delta x_0}^2 & = & b_1 & = & S_1'(x_1) \\
S_1'(x_2) & = & b_1 & + & 2c_1{\Delta x_1} & + & 3d_1{\Delta x_1}^2 & = & b_2 & = & S_2'(x_2) \\
& & & & & \vdots \\
S_j'(x_{j+1}) & = & b_j & + & 2c_j{\Delta x_j} & + & 3d_j{\Delta x_j}^2 & = & b_{j+1} & = & S_{j+1}'(x_{j+1}) \\
& & & & & \vdots \\
S_{n-2}'(x_{n-1}) & = & b_{n-2} & + & 2c_{n-2}{\Delta x_{n-2}} & + & 3d_{n-2}{\Delta x_{n-2}}^2 & = & b_{n-1} & = & S_{n-1}'(x_{n-1}) \\
\end{matrix}
\end{eqnarray}
}
条件3より
\begin{eqnarray}
\begin{matrix}
S_0''(x_1) & = & 2c_0 & + & 6d_0{\Delta x_0} & = & 2c_1 & = & S_1''(x_1) \\
S_1''(x_2) & = & 2c_1 & + & 6d_1{\Delta x_1} & = & 2c_2 & = & S_2''(x_2) \\
&&&\vdots \\
S_j''(x_{j+1}) & = & 2c_j & + & 6d_j{\Delta x_j} & = & 2c_{j+1} & = & S_{j+1}''(x_{j+1}) \\
&&&\vdots \\
S_{n-2}''(x_{n-1}) & = & 2c_{n-2} & + & 6d_{n-2}{\Delta x_{n-2}} & = & 2c_{n-1} & = & S_{n-1}''(x_{n-1}) \\
\end{matrix}
\end{eqnarray}
条件4より
\begin{eqnarray}
\begin{matrix}
S_0''(x_1) & = & 2c_0 & & & = & 0 \\
S_{n-1}''(x_n) & = & 2c_{n-1} & + & 6d_{n-1}{\Delta x_{n-1}} & = & 0 \\
\end{matrix}
\end{eqnarray}
求解法
これらの連立方程式を行列計算で解く。
(例)データ
\begin{eqnarray}
y_0 &=& f(x_0) \\
y_1 &=& f(x_1) \\
y_2 &=& f(x_2) \\
y_3 &=& f(x_3) \\
\end{eqnarray}
という4つのデータ点を補間する場合。
\scriptstyle{
X=
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & \Delta x_0 & {\Delta x_0}^2 & {\Delta x_0}^3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 &1 & \Delta x_1 & {\Delta x_1}^2 & {\Delta x_1}^3 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & \Delta x_2 & {\Delta x_2}^2 & {\Delta x_2}^3 \\
0 & 1 & 2{\Delta x_0} & 3{\Delta x_0}^2 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 3{\Delta x_0} & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 2{\Delta x_1} & 3{\Delta x_1}^2 & 0 & -1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 3{\Delta x_1} & 0 & 0 & -1 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 3{\Delta x_2} \\
\end{bmatrix}
\\
A = \begin{bmatrix}
a_0 \\ b_0 \\ c_0 \\ d_0 \\ a_1 \\ b_1 \\ c_1 \\ d_1 \\ a_2 \\ b_2 \\ c_2 \\ d_2
\end{bmatrix}
, \quad
Y = \begin{bmatrix}
y_0 \\ y_1 \\ y_1 \\ y_2 \\ y_2 \\ y_3 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0
\end{bmatrix}
}
XA = Y \\
A = X^{-1}Y
別解 (お勧めしません)
各条件式から移行や代入をして整理すると以下が得られる。
\begin{eqnarray}
a_j &=& y_j \\
b_j &=& \frac{y_{j+1} - y_j}{\Delta x_j} - \frac{{\Delta x_j}(c_{j+1} + 2c_j)}{3} \\
d_j &=& \frac{c_{j+1} - c_j}{3{\Delta x_j}}
\end{eqnarray}
{\Delta x_j}c_j + 2(\Delta x_{j+1} + \Delta x_j)c_{j+1} + {\Delta x_{j+1}}c_{j+2} = \frac{3(y_{j+2} - y_{j+1})}{\Delta x_{j+1}} - \frac{3(y_{j+1} - y_{j})}{\Delta x_{j}}
$c_j$を工夫して求められれば他も求まる。
ここまでの内容は以下に書きました。
スプライン補間について(その2)
なぜ「3次」スプライン曲線なのか
〇 1次、2次だと「連続的でなめらか」に曲線がつながらない
〇 4次以上だと平面グラフにおいては数学的、物理的に意味がない
〇 曲線を連続体とみたとき、曲げの弾性エネルギーを最小にする曲線が3次曲線
だから。
xy平面上に描くグラフに適用するなら3次スプライン曲線が適切。
この内容は以下に書きました。
スプライン補間について(その3)
物理量最適化によるスプライン曲線の次数決定
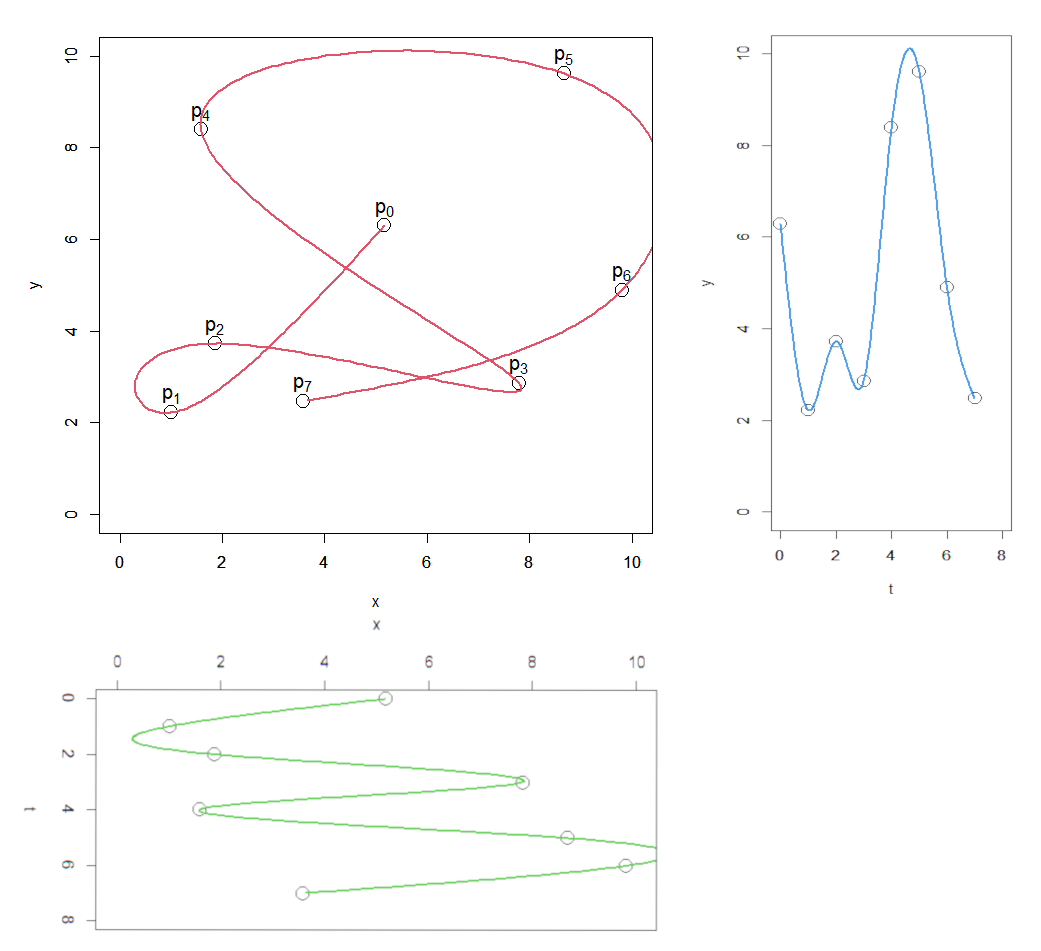
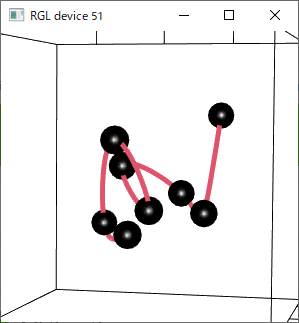
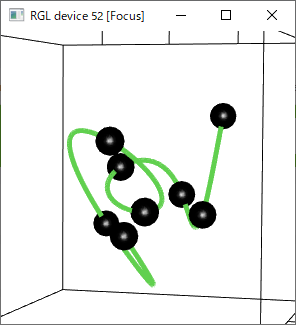
空間内運動データへの適用
データ点に順番があり、かつ、どの座標変数の間にも従属関係がなく独立な場合、データ点は空間内運動データと捉えることができる。
その場合、この空間内運動データをパラメータ t を用いてスプライン補間することができる。
また、t を
t = 0,1,2,3,\cdots
とすることで、行列を簡単かつどの座標変数に対しても同一にすることができる。
\begin{matrix}
x_0=x(t_0)=x(0) & x_1=x(t_1)=x(1) & x_2=x(t_2)=x(2) & \cdots & x_j=x(t_j)=x(j) & \cdots \\
y_0=y(t_0)=y(0) & y_1=y(t_1)=y(1) & y_2=y(t_2)=y(2) & \cdots & y_j=y(t_j)=y(j) & \cdots \\
z_0=z(t_0)=z(0) & z_1=z(t_1)=z(1) & z_2=z(t_2)=z(2) & \cdots & z_j=z(t_j)=z(j) & \cdots \\
w_0=w(t_0)=w(0) & w_1=w(t_1)=w(1) & w_2=w(t_2)=w(2) & \cdots & w_j=w(t_j)=w(j) & \cdots \\
\vdots & \vdots & \vdots & \cdots & \vdots & \cdots \\
\end{matrix}
( データ点のスプライン補間を、座標軸ごとに行うことができる )
2次元平面内運動データの場合
$(t_{j+1} - t_j) = \Delta t_j = 1$ に注意すると行列 X は以下になる。
\scriptstyle{
X=
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 1 & 2 & 3 & 0 & -1 & 0 & 0 \\
0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 3 & 0 & 0 & -1 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 3 \\
\end{bmatrix}
}
尚、x軸, y軸に対して用いる行列は共にこの行列 X である。
($XA=Y$ の解行列 $Y$ に適切にデータ値を並べてから計算)
このようにx軸、y軸別々に求めても、
・連続性
・傾きの一致
・曲率の一致
は保証される。
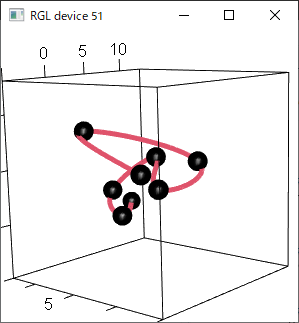
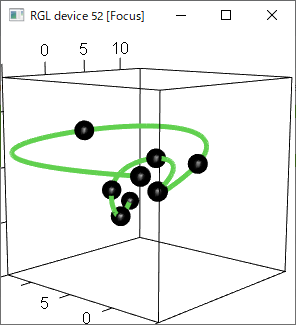
3次元空間内運動データの場合
3次元では
・連続性
・傾きの一致
・曲率の一致
に加えて
・捩率の一致
が必要。
それに従い、3次スプライン曲線では実現できない。
4次スプライン曲線 を用いる必要がある。
2次元の時と同じく、$\Delta t_j = 1$ を用いると、x軸、y軸、z軸それぞれと時刻 t との間に使う行列は同一。
以下の通り。
\tiny{
X=
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \\
0 & 1 & 2 & 3 & 4 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 2 & 3 & 4 & 0 & -1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 1 & 2 & 3 & 4 & 0 & -1 & 0 & 0 & 0 \\
0 & 0 & 1 & 3 & 6 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 3 & 6 & 0 & 0 & -1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 3 & 6 & 0 & 0 & -1 & 0 & 0 \\
0 & 0 & 0 & 1 & 4 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 4 & 0 & 0 & 0 & -1 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 & 4 & 0 & 0 & 0 & -1 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 4 \\
\end{bmatrix}
}
高次元の場合
その次元の対応する 一般化曲率 を合わせる必要があるため、それに必要な微分量も一致させる必要がある。
そのため、次元が上がるにつれ必要な多項式の次数も上がっていく。
ここまでの内容は以下に書きました。
スプライン補間について(その4)
スプライン補間を使用するにあたっての注意
スプライン補間の適用で間違いやすいと思う点を2つ指摘する。
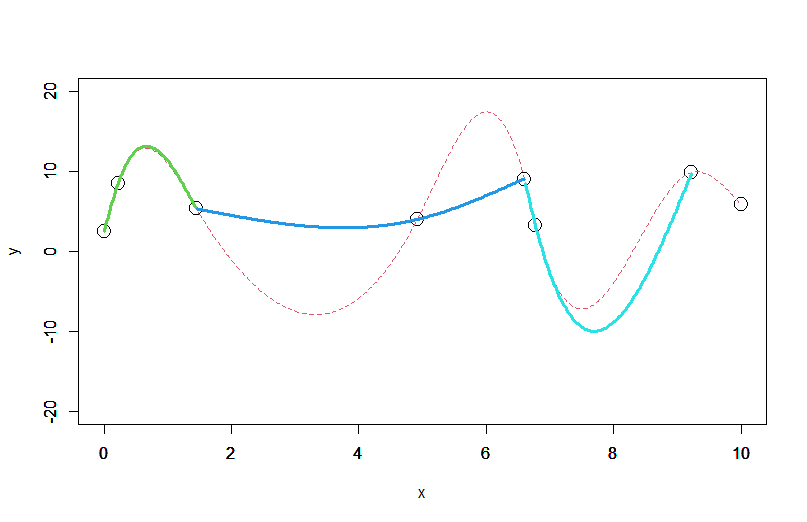
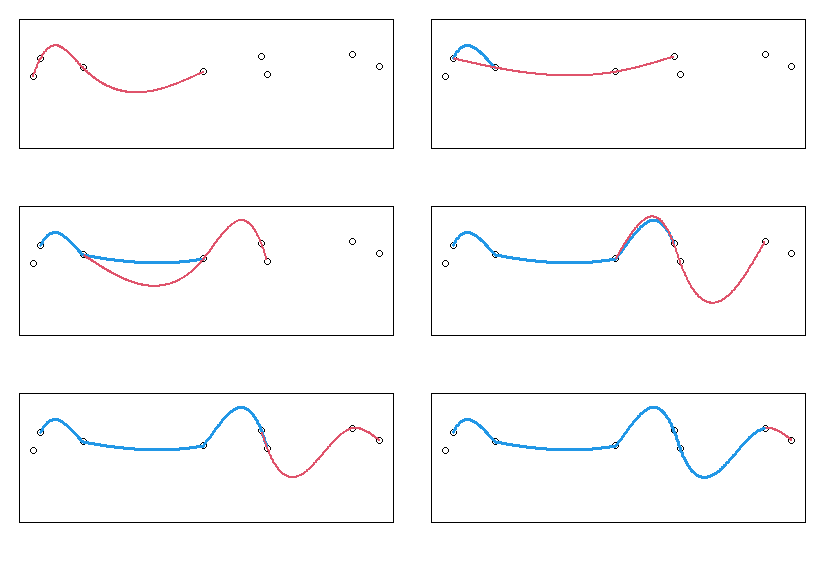
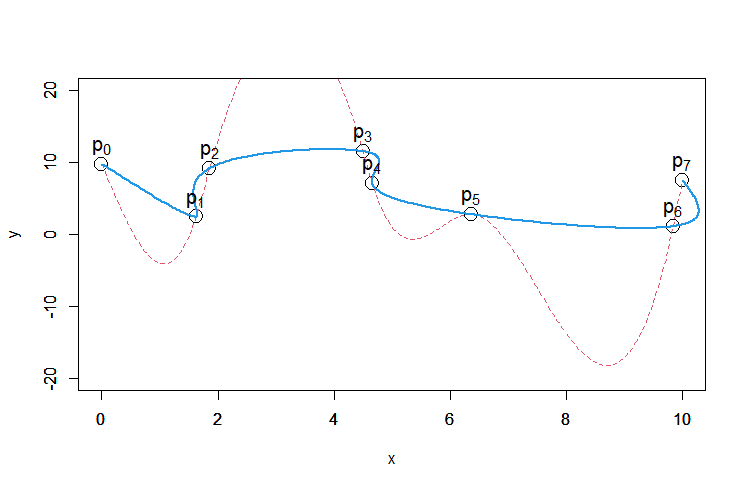
スプライン補間の逐次適用
スプライン補間を逐次適用してはいけない
スプライン補間は、必要な区間全体に対し一括して適用しなければいけない。
全区間の区分多項式を一括で求めなければいけない。
逐次適用して求めた場合、継ぎ足しした点で微分量の不連続が起きる。
曲線が折れ曲がったり(傾きの不一致)、急激に曲がったり(曲率の不一致)。
継ぎ足し継ぎ足しでスプライン補間を使ってはいけません。
時系列データにスプライン補間を適用する場合は注意!
逐次スプライン補間についてはこちら
y=f(x)の関係があるデータへのパラメータ t を使ったスプライン補間
x が独立変数(説明変数)、y が従属変数(目的変数)であるような関係のデータ、つまり、$y=f(x)$であるようなデータに、媒介変数 t を用いて x、y 別々でスプライン補間を行って後で合わせる方法を用いてはいけない。
つまり、
$y=f(x)$であるようなデータには、$x=x(t), y=y(t)$としてバラバラにスプライン曲線を求めてはいけない
パラメータ(媒介変数) t を用いてそれぞれの軸ごとにスプライン曲線を求めてよいのは、x, y が共に独立変数の場合に限る。
さらに高次元の場合にも、各軸の変数はすべて互いに独立変数である場合に適用ができ、ひとつでも従属変数がある場合には適用できない。
$y=f(x)$ のデータの場合、$x=x(t)$とすると、
\begin{eqnarray}
x &=& x(t) \\
y &=& f(x(t)) \\
&=& (f \circ x)(t)
\end{eqnarray}
と、y は合成関数で表されなけらばならない事に注意
ここまでの内容は以下に書きました。
スプライン補間について(その5)
おわり
以上です。
間違いなどありましたら、お教えいただければ幸いです。
時系列データなどの時に補間を逐次適用していくためにはどうすればいいのか、についてはまた別の機会に書けたらいいなと思います。
皆さんのお役に立てれば幸いです。
感想など頂けると嬉しいです。
お読み頂きありがとうございました。