前回からの続きです。
こちらを先に読んでからの方がよいかと思います。
スプライン補間について(その1)
スプライン補間について(その2)
スプライン補間について(その3)
スプライン補間について(その4)
6.スプライン補間を使用するにあたっての注意
ここでは、スプライン補間を使用するにあたって注意しなければならない事を書いていきます。
利用する際の参考にしてもらえれば幸いです。
補間区間への逐次適用と一括適用
ここまで見てきたように、スプライン補間は全補間区間を一括で計算して求めます。
データ点が n+1個あって、補間区間が n個、つまり区分多項式が n個あったら、4n個の係数を一括で計算して全区間多項式を明らかにします。
これは結構大変です。
データ点が少ない間はいいですが、データ点が増えてくると計算する行列のサイズは4ずつ増えていくので、巨大行列を計算することになってしまいます。
データ点が10個で$4 \times (10-1)=36$ で36次元の行列計算、データ点が20個になれば$4 \times (20-1)=76$で76次元の行列計算です。
使うライブラリやプログラムによっては計算不可になることが出てきます。
また、常に新しい値を取得し続けていくようなリアルタイム時系列解析のような場面では、これを計算することは不可能です。
行列のサイズがいつまでたっても決まらないし、データもそろわないからです。
そこで、適用する区間数をあらかじめ決めて、それを順次ずらして逐次的に適用していくことが考えられます。
このように利用している方も多いかと思います。
さて、ここで疑問になるのが、
全区間で一括で計算して求めたスプライン曲線と、小区間で逐次計算して求めたスプライン曲線は同じになるのか
ということです。
これが同じであるならば、わざわざ巨大行列を計算して一括で求めなくても、ある区間数で行列サイズを決めて、それを逐次適用していくだけでよいです。
プログラムで処理する場合、関数化(古い言葉でサブルーチン化、プロシージャ化、最近ではメソッド化かな)することができるので、逐次この関数に放り込むだけで連続してスプライン補間の結果が得られて便利です。
先に答えを言ってしまえば、残念ながら
スプラインの一括適用計算と逐次適用計算では、得られる曲線は異なる
となります。
ではどのくらい異なるのか、視覚的に確かめてみようと思います。
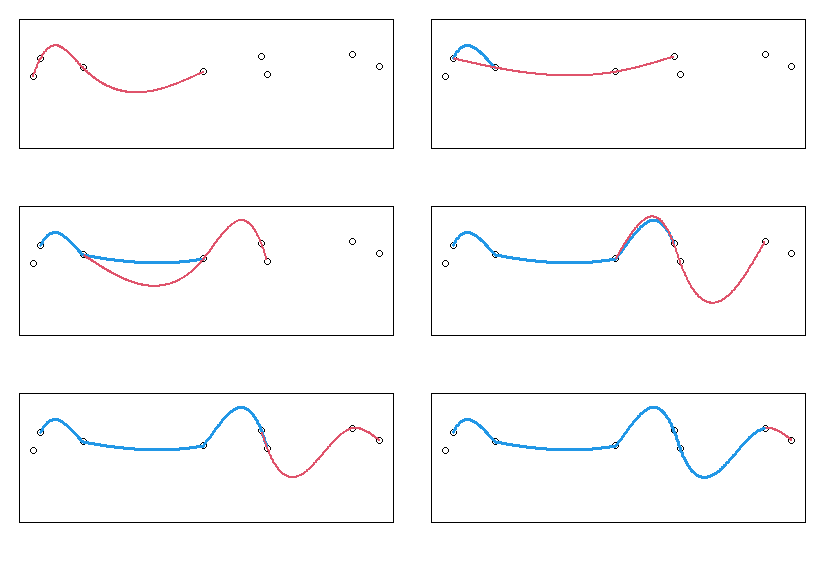
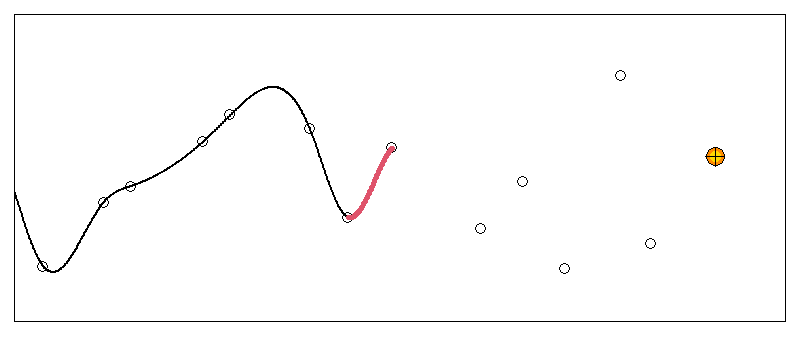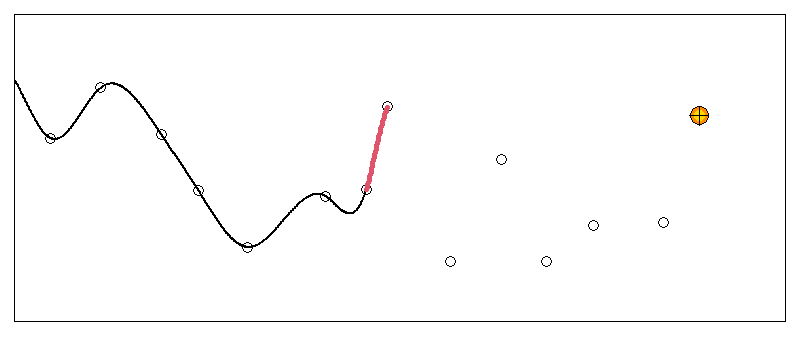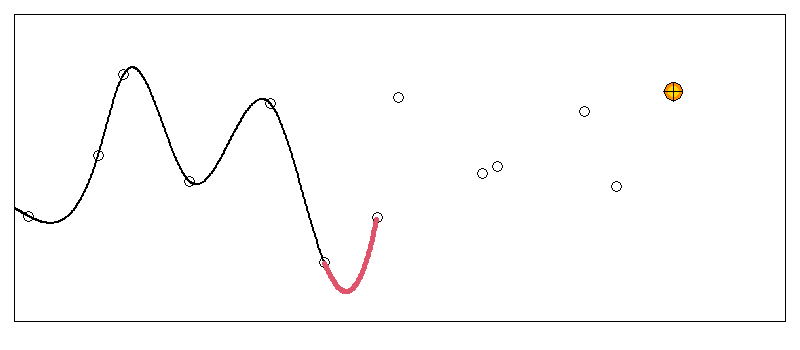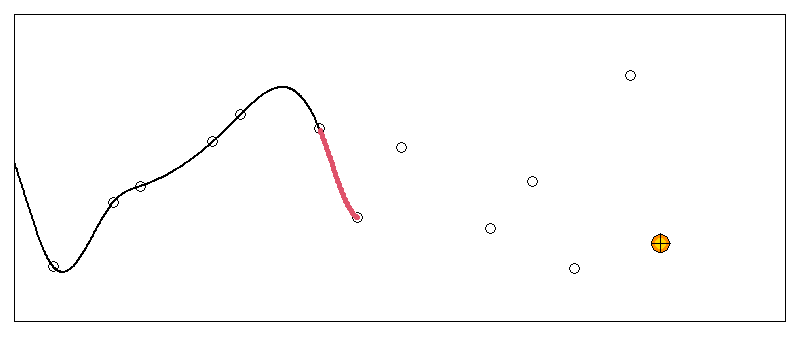
区間ごとに適用してつなぎ合わせた場合
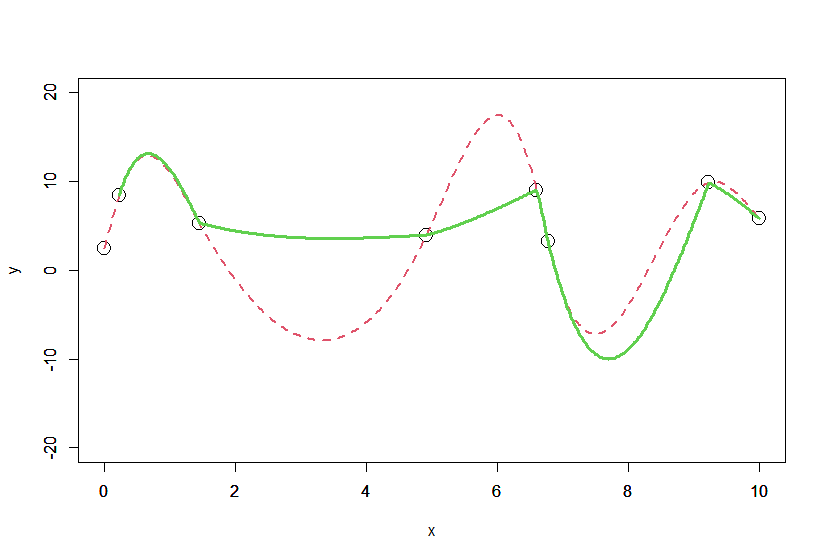
以下のグラフは、データ点3点ごとに3次スプライン曲線を求め、つなぎ合わせたものです。
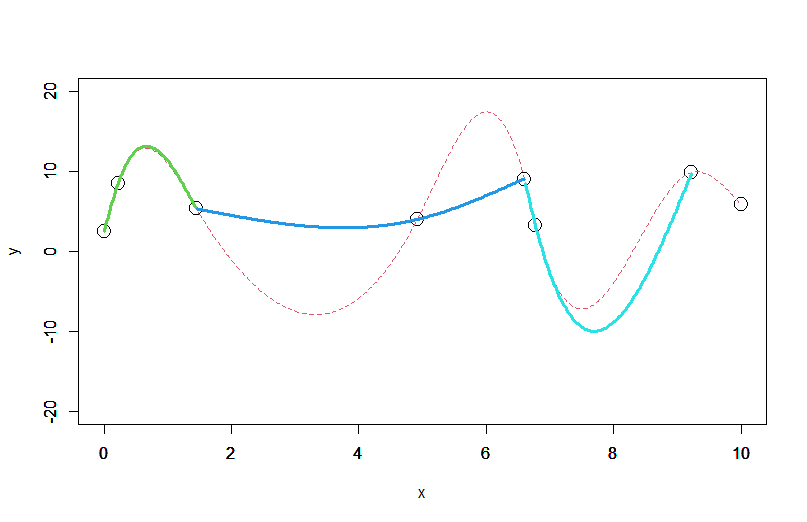
つなぎ合わせた点(3点ごと)で滑らかにつながっておらず、傾きが不連続になっているのが分かります。
接続点で傾きを一致させるように構成していないので当然そうなります。
赤の点線が全区間で一括して求めたスプライン曲線ですが、だいぶ違った形をしていることが分かります。
接続点で傾きを一致させていないのなら、これが4点ごとでも5点ごとでも、n点ごとでもつなぎ合わせた点で不連続になるのは同じです。
なので、区間ごとに適用してつなぎ合わせるこの方法では連続性は保たれないことが分かります。
移動ウィンドウ法で逐次適用する場合
時系列解析をする方なら移動ウィンドウでデータを処理することが多いと思います。
スプライン補間を移動ウィンドウで処理した場合はどうなるでしょうか?
〇 連続3点でスプライン補間をして、2つ目の区間をつなぎ合わせた場合
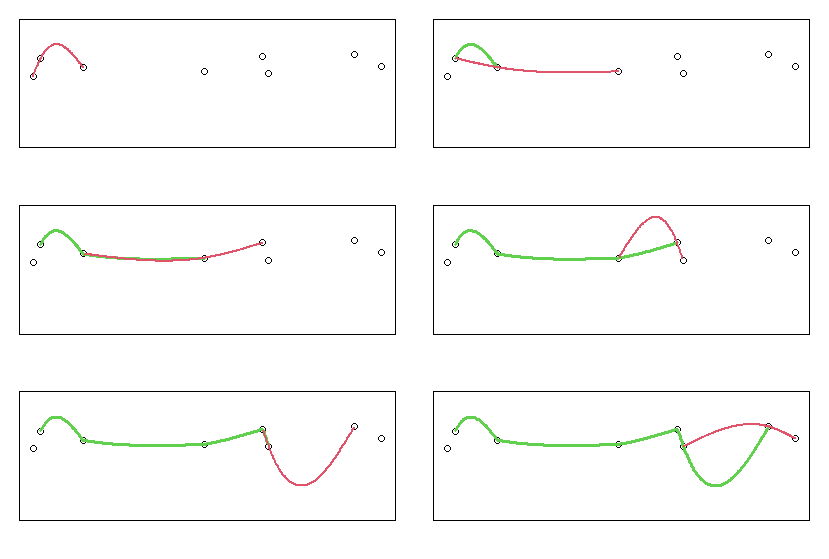
〇 連続4点でスプライン補間をして、真ん中の区間をつなぎ合わせた場合
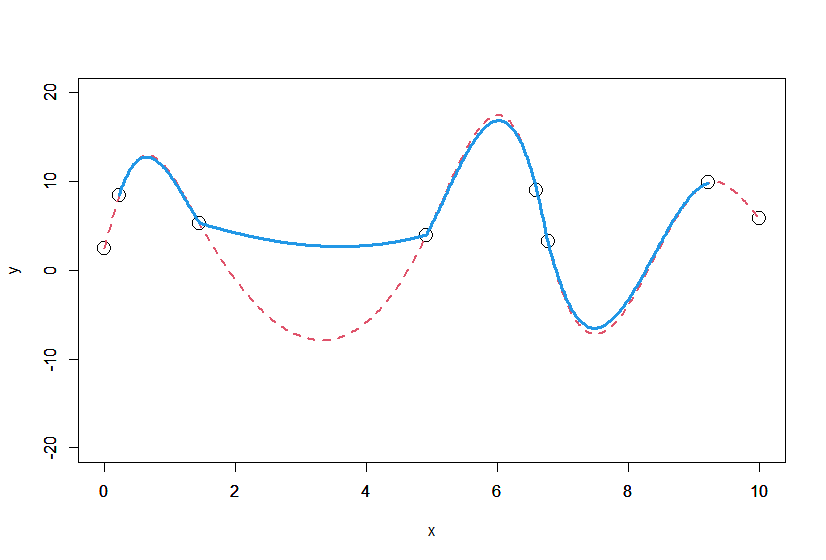
見て分かる通り、どちらの場合も接続点で傾きが不連続になっています。
「端」ではなく、「途中」の接続点を合わせていっても不連続が発生することが分かります。
これは、逐次処理する区間点を増やして5点、6点としていっても同じです。
つなぎ目の境界点で連続性を担保していないので、ほぼ確実に不連続になってしまいます。
逐次適用に関しての結果
以上より、スプライン補間は継ぎ足して適用した場合、スプライン補間の目的である
自然に滑らかにデータを補間するという目的が果たされない
ことが分かります。
これは、スプライン補間を求めるときの求め方からもわかります。
すべての区間に対する連立方程式を解いているので、
すべての区間の全係数が互いに関係しあう
からです。
連立方程式というのはそういうものでした。
どの区間の曲線の形も全区間に影響を及ぼすというわけです。
よって、これまで見てきたスプライン曲線の求解法を用いる場合、
対象とする区間全部に一括して適用する必要があり、逐次適用してつなぎ合わせてはいけない
ことが分かりました。
時系列解析にスプライン補間を用いている方、お気をつけください。
ではどうすれば、逐次処理の際にデータ点を自然に補間することができるのか。
こんなことを実現するにはどうすればよいのか。
これについては こちら に書きましたので、よければ読んでみてください。
xとyが独立でないグラフにパラメータ手法を適用した場合
パラメータ $t$ を使って空間内運動にスプライン補間を適用する方法を述べた時にも少し触れました。
\begin{eqnarray}
x &=& x(t) \\
y &=& y(t)
\end{eqnarray}
として$x, y$それぞれとパラメータ $t$との間のスプライン曲線を求め、それを合わせて$xy$平面上のデータ点をスプライン補間する場合の条件は
$x$と$y$が共に独立変数であること
でした。
つまり、
y = f(x)
という形の、
$x$ が独立変数(説明変数)、$y$ が従属変数(目的変数)であるような場合には適用できません。
先にも書いた通り、パラメータ(媒介変数) t を用いた場合において時刻を自然数にした場合は係数を求める為の行列が固定されるので処理を書きやすく便利です。
なのでプログラム書く側としては $y=f(x)$の場合にも使いたくなってしまいます。
他のサイトでも、このようにパラメータ t を用いた処理で書けば便利であると書かれているサイトもありました。
しかし、適用してはいけないのです。
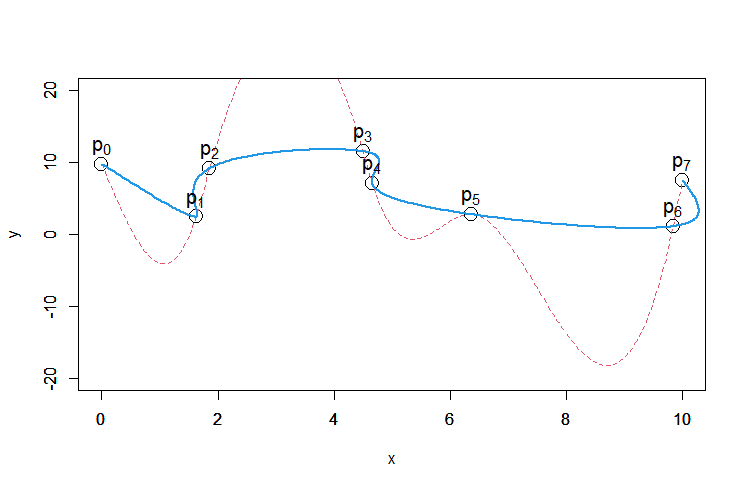
では適用するとどうなるのか、実際に適用したものを見てみます。
これは一例ですが、このような形の補間曲線がそれなりの高頻度で出現します。
赤の点線が $y=f(x)$としてスプライン補間を適用した線。
青の実線が
t = 0, 1, 2, 3, 4, 5, 6, 7 \\
x=x(t)\\
y=y(t)
としてスプライン曲線を求め、結果を$xy$として描画した線です。
一目でわかると思いますが、これは $y=f(x)$ のグラフの補間としては不適格です。
データ点$p_1 \sim p_2$、$p_3 \sim p_4$、$p_6 \sim p_7$で補間線がx軸マイナス方向へ戻ってしまっている箇所があります。
これは $y=f(x)$ を満たさない事は明らかです。
戻りが発生しているということは、その区間の $x$の値に対して、$y$の値が2つ以上存在するということだからです。
その区間の $x$の値のところに垂直に線を引けば、曲線と2回以上交差します。
2回以上交差するということは、$y$の値が2つ以上あるということ。
$y=f(x)$という一価関数のグラフとしては不適格です。
この 戻り現象 がいつも起こるとは限りませんが、めったに起こらないわけでもありません。
数学的にこの手法が不適格なのは明らかです。
これはある意味当たり前です。
媒介変数 $t$ によって時刻 $t_j$ にデータ $x_j, y_j$ が取得されたとして、それを
x_j=x(t_j), \quad y_j=y(t_j)
としたのですから、ここには x と y の間になんの関係も規定していません。
つまり、お互いに "独立である" としているわけです。
お互い独立なのですから、x の値に複数の y が該当しようと、y の値に複数の x が該当しようとよいわけです。
一価関数である$y=f(x)$の 「x の値に対し y の値はひとつだけ」 という事情は酌んでくれません。
しかし、このように考えるかもしれません。
$y=f(x)$だとしても、ある時刻 $t_j$ にデータ $x_j, y_j$ が同時に得られたことには変わりない。
そのとき、この時刻 $t_j$ が1秒おきであっても問題ないだろう。
ならば、パラメータ t を使って計算しても問題ないはずだ。
確かにその通りです。
しかし、こう考えた場合でも上のように単純に$x=x(t), y=y(t)$ としてはいけません。
なぜなら、xの値に対してyの値が一つ決まるのですから、$y=f(x)$。
つまり、
\begin{eqnarray}
x &=& x(t) \\
y &=& f(x(t)) \\
&=& (f \circ x)(t)
\end{eqnarray}
であるわけです。
つまり、y は時刻 t の関数とみることができますが、それは x を介した 合成関数 としてみるということになります。
時刻 $t_j$ の時、xの値は(xが独立変数なので)$x_j=x(t_j)$ としてよいですが、y の値は
\begin{eqnarray}
y_j &=& f(x(t_j)) \\
&=& f(x_j)
\end{eqnarray}
としなければならないということです(そもそも y は従属変数です)。
もしくは、t を直接使うならば、
\begin{eqnarray}
x_j &=& x(t_j) \\
y_j &=& (f \circ x)(t_j)
\end{eqnarray}
として、$(f \circ x)$という合成関数の形を具体的に求めなくてはなりません。
そして、この合成関数の形を求める条件設定は、これまでの媒介変数 t を用いたスプライン曲線を求める手法に入っていません。
よって結果は意図したとおりになりません。
これが、$y=f(x)$ の形のグラフに媒介変数 t を用いた別々にスプライン曲線を求める手法を単純に適用してはいけない理由です。
これは3次以上の高次元に適用する場合においても同様です。
パラメータ t を用いてそれぞれでスプライン補間を求める手法を使用するときは、
出てくる変数が互いに独立
である場合にのみ使用するようにしてください。
そうしないとそのスプライン補間を使用して導かれる結果が信用できないものになります。
もし $y=f(x)$のような従属変数を含むグラフにこのパラメータ t でそれぞれ求める手法を適用している方がいましたら、修正することをお勧めします。
今回のまとめ
スプライン曲線を使用するとき
・対象とするすべての区間を一括で処理して求解しなくてはいけない。
・すべての区間の区分多項式をすべて連立させた連立方程式を解いて求めなければならない。
・前から、後ろから、など対象とする区間を小区間に区切って小区間ごとにスプライン曲線を求めてつなぎ合わせてはいけない。
・時系列の逐次処理に用いてはいけない。
グラフに適用するとき
・従属変数があるグラフに、媒介変数 t を用いた求解法を単純適用してはいけない。
・$y=f(x)$ の関係があるグラフに
\begin{eqnarray}
x &=& x(t) \\
y &=& y(t) \\
(t &=& 1,2,3,\cdots ) \\
\\
x_1 &=& x(t_1), \quad x_2 = x(t_2), \cdots , x_j = x(t_j), \cdots \\
y_1 &=& y(t_1), \quad y_2 = y(t_2), \cdots , y_j = y(t_j), \cdots \\
\end{eqnarray}
という、x と y をそれぞれ別々で求める手法を単純適用してはいけない。
・パラメータ t を使って x と y を別々にスプライン補間して求める方法は、x と y が互いに独立変数であるときにしか用いてはいけない。
つづく
次回はまとめで終わります。